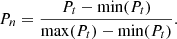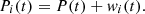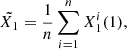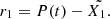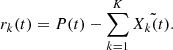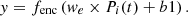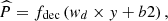| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 7 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.2516/stet/2024001 | |
| Published online | 26 January 2024 | |
Regular Article
A multi-step electricity prediction model for residential buildings based on ensemble Empirical Mode Decomposition technique
1
Computer Science and Engineering Department, Thapar Institute of Engineering and Technology, Bhadson Rd, Adarsh Nagar, Prem Nagar, Patiala, Punjab 147004, India
2
Computer Application Department, National Institute of Technology, Kurukshetra, Haryana 136119, India
* Corresponding author: skaur60_phd19@thapar.edu
Received:
19
August
2023
Accepted:
3
January
2024
Residential electricity demand is increasing rapidly, constituting about a quarter of total energy consumption. Electricity demand prediction is one of the sustainable solutions to improve energy efficiency in real-world scenarios. The non-linear and non-stationary consumption patterns in residential buildings make electricity prediction more challenging. This paper proposes a multi-step prediction approach that first conducts cluster analysis to identify seasonal consumption patterns. Secondly, an improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) method and autoencoder model has been deployed to remove irregular patterns, noise, and redundancy from electricity load time series. Finally, the Long Short-Term Memory (LSTM) model has been trained to predict electricity consumption by considering historical, seasonal, and temporal data dependencies. Further, experimental analysis has been conducted on real-time electricity consumption datasets of residential buildings. The comparative results reveal that the proposed multi-step model outperformed the existing state-of-the-art RF-LSTM-based prediction model and attained higher accuracy.
Key words: Electricity consumption prediction / Residential buildings / Cluster analysis / Empirical Mode Decomposition
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Buildings and industry are currently the largest power consumers, accounting for more than 90% of global electricity consumption, as per the report of the International Energy Agency (IEA), 2022 [1]. Moreover, the energy consumption industry in India is anticipated to increase from 20% to roughly 50% by 2040. According to the report of IEA, 2022 [1], the industrial sector consumes the maximum electricity (44%), followed by the residential sector (24%), which is a quarter of the total energy consumption as seen in Figure 1. The alarmingly rising energy consumption is a serious concern for energy suppliers and utility companies. Thus, energy efficiency techniques must be developed to reduce electricity consumption. Predicting energy consumption plays a vital role in increasing energy efficiency. It is a foundation for many energy management, monitoring, and optimization methods that provide residential buildings usage patterns [2]. In the past decade, many researchers have proposed electricity demand forecasting techniques [3] based on machine learning algorithms such as Support Vector Regressor (SVR) [4], Random Forest [5], Decision Trees (DT) [6], Artificial Neural Network (ANN) [7], Convolutional Neural Networks (CNN) [8] and Multi-Layer Perceptron (MLP) [9]. However, the traditional machine learning approaches suffer from substantial deficits, such as non-adaptability, inability to handle long-term dependencies, and inaccurate predictions [10]. Among these algorithms, neural networks show promising results in predictive analysis, anomaly detection, and pattern recognition [11, 12]. However, these models may have certain problems, such as over-fitting, hyperparameter selection, significant training time, etc. To overcome these deficiencies, a few authors [13–15] have proposed hybrid approaches that combine data decomposition techniques with prediction models. Still, there is a need to develop an improved approach to investigate and predict electricity consumption in real-world scenarios. The present research proposes a multi-step prediction approach that integrates the season-wise cluster analysis and Improved Complete Ensemble Empirical Mode Decomposition with the Adaptive Noise (I-CEEMDAN) method, autoencoder, and Long Short-Term Memory (LSTM) model. The paper is organized as follows: Section 2 discusses the background of the energy prediction models. Further, Section 3 explains the methodology of the proposed approach, and Section 4 discusses the experimental results obtained by the proposed prediction model. Finally, Section 5 provides the conclusion of the proposed work.
2 Background
Several researchers have done significant research to predict energy consumption in residential buildings by deploying various machine learning and deep learning techniques [16]. Some authors have used data clustering techniques to analyze energy consumption patterns and trends. The following subsection summarizes the latest energy prediction research using data clustering, machine learning, and hybrid techniques.
2.1 Energy prediction: cluster-based approaches
Few authors have employed data clustering algorithms to get meaningful insights out of the energy consumption scenarios. Kaur and Bala [17] have proposed an energy prediction technique based on K-means clustering to fetch energy usage patterns of home appliances in residential buildings. RF model has been trained for predictive analysis using the climate conditions along with energy consumption data of home appliances. Chinthavali et al. [18] have identified similar weather day/weak pairs to compare the energy cost with and without applying optimization. Verma et al. [19] have proposed an energy consumption optimization approach for various home appliances grouped into clusters based on similar usage behavior. Further, Luo et al. [20] have performed feature extraction on weather data using K-means clustering and created weather clusters. Later, the authors predicted the week-ahead hourly energy consumption by employing GA-DNN. Season-wise cluster formation has been proposed by Bedi et al. [21] based hierarchical clustering algorithm. The extracted clusters have been used for energy prediction of different seasons of the year. Therefore, the extracted cluster data can be used to develop an energy prediction model using machine-learning approaches. The subsequent section explored various machine learning techniques to predict energy consumption.
2.2 Energy prediction: machine learning-based approaches
Several machine learning algorithms have been widely adopted to predict the energy consumption of residential as well as other buildings. Jain et al. [10] have proposed an energy forecasting model based on the SVM algorithm for multi-family buildings and concluded that the spatial and temporal features improved the predictive performance. They also suggested the necessity of the installation of smart meters to get high-resolution energy consumption data. The authors, Wahid et al. [22], have developed an energy consumption prediction for residential buildings using MLP and RF for appliance classification. They analyzed the on-off times of home appliances based on electrical usage data. Huber et al. [23] also analyzed the on-off times of home appliances and predicted the energy using histograms, pattern search, and Bayesian algorithms. Tiwari et al. [2] have deployed logistic regression, decision tree, Support Vector Machine (SVM), naive Bayes, RF, and k-nearest neighbor algorithms for energy prediction of smart grids and determined that SVM outperformed in accuracy.
Besides traditional machine learning algorithms, the authors [24] have proposed a neural network-based energy prediction model. They have optimized the neural networks using the shark smell optimization algorithm. The hybrid prediction model has been used to estimate the energy load of small-scale buildings. Fan et al. [25] have proposed deep learning-based models to construct the features automatically and applied fully connected and convolutional autoencoders to improve energy predictions. Bourhnane et al. [7] have implemented an energy prediction and scheduling approach for smart buildings using ANN and genetic algorithms. A big data analytics-based energy prediction model has been proposed by Kumari et al. [26]. The LSTM model and the genetic algorithm have been applied to estimate the energy consumption of residential buildings. Furthermore, for individual household appliances, Kaur et al. [27] have proposed an intelligent energy prediction and optimization approach based on an LSTM model and genetic algorithm.
2.3 Energy prediction: hybrid approaches
Some authors have integrated the data decomposition techniques with the prediction model to achieve optimal performance. The effectiveness of the decomposition techniques can be seen in their results [14, 28]. For instance, An et al. [29] have deployed an Empirical Mode Decomposition (EMD) and Feedforward Neural Network (FNN) model to forecast the future energy demand in the residential sector. Liu et al. applied EMD to decompose the non-stationary time series data and developed SVR models for each decomposed signal. The hybrid EMD-SVR technique produced better results than the SVR model. Bedi et al. [13] combined EMD with the LSTM model to predict the real-time electricity consumption of buildings. The EMD algorithm decomposed time series signals into various Intrinsic Mode Functions (IMFs), prepared an individual prediction model for each IMF, and added them to produce aggregated energy predictions.
Even though the EMD improved the prediction performance, but reconstructed signal or the aggregated predictions include residual noise. To resolve the issue, Wu and Huang [30] have proposed an Ensemble Empirical Mode Decomposition (EEMD) method in which white noise was added to eliminate the mode mixing problem. However, EEMD suffers from high computational time. Colominas et al. [31] proposed CEEMDAN with improved decomposition ability and reduced computational time. It adds an adaptive noise at each level of decomposition. Chai et al. [15] have proposed a hybrid feature-driven ensemble forecasting model based on extreme learning machine and particle swarm optimization. The time-series data has been decomposed and reconstructed by Variational Mode Decomposition (VMD) and sample entropy algorithm. Karijadi et al. [14] utilized CEEMDAN to decompose the non-stationary time series signals. Next, RF and LSTM models have been deployed to predict each extracted IMF.
The above literature review has emphasized the significance of improving energy prediction performance. However, the energy prediction of real-time residential buildings becomes critical due to non-linear fluctuating energy consumption patterns. Moreover, seasonal variations, usage patterns, and the number of occupants have mainly influenced energy consumption in buildings. The research challenges and novel contributions of the proposed work are described as follows:
2.4 Research challenges and our contributions
-
Several authors have implemented clustering to observe the energy consumption scenarios in the residential sector [17, 21, 32]. Still, the impact of seasonal variations of energy consumption needs to be explored using a real-time environment. In this paper, real-time data clustering has been done to analyze the effect of climatic conditions on electricity consumption patterns in residential buildings.
-
The non-linear and fluctuating nature of the time series dataset makes the energy prediction task challenging [14]. The present work handles the load fluctuations and non-linearity by decomposing the original real-time dataset into a set of Intrinsic Mode Functions (IMFs) using an improved CEEMDAN method. For each extracted mode components
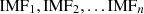 , the autoencoder model is deployed to reconstruct the decomposed signal.
, the autoencoder model is deployed to reconstruct the decomposed signal. -
Further, the reconstructed data provided by the autoencoder model is used by the LSTM model to learn the non-linear features and underlying patterns accurately to improve its prediction performance [13]. The proposed work integrates the LSTM model with an improved CEEMDAN method. The sliding window approach has been used to generate an input window and feed it into the LSTM model to address long-term data dependencies.
-
Most authors have adopted noise-free static, benchmark, or public energy consumption datasets to evaluate prediction models [11, 33]. The proposed work exploits the real-time electricity consumption dataset to evaluate the hybrid prediction model.
3 Proposed methodology
The proposed work aims to predict the energy demand of residential buildings using real-time electricity consumption data. Electricity demand prediction is driven by the correctness and reliability of historical data. Real-time electricity data collection is affected by smart meters malfunctioning, changing weather conditions, communication issues, etc. These factors may create undesired noise and uncertainties in the electricity consumption dataset. The present work considers the seasonality of data and identifies similar energy consumption patterns using Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH) clustering, which preprocesses and summarizes the whole dataset. Further, the proposed work deploys an I-CEEMDAN-based noise removal approach to decompose the electricity consumption signals into sub-signals. For each extracted sub-signal, the autoencoder model performs the reconstruction of the decomposed input signal. Ultimately, the LSTM neural network model will be applied to estimate the electricity demand. The methodology to implement the proposed research is illustrated in Figure 2. Each module of the proposed work is detailed in the following subsections.
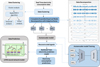 |
Figure 2 Proposed electricity consumption forecasting approach for residential buildings. |
3.1 Real-time dataset description and preprocessing
The proposed work has exploited real-time data for estimating future electricity demand. Real-time data is more actionable and reliable and exhibits unpredictable events, weather changes, and changing user behavior [16]. The prediction models developed for real-time data are more adaptive to a wide range of scenarios. The real-world residential buildings’ electricity consumption dataset has been taken from Punjab State Power Corporation Limited (PSPCL), Punjab, India [34]. The dataset recorded the actual energy consumed (kWh) by consumers of residential buildings for a period of 1 year. The dataset consists of multi-family and single-family residential buildings. While the selected buildings exhibit heterogeneous consumption patterns and trends, as seen in Figure 3. The data exploration shown in Figure 3 reveals that each building exhibits non-linear and non-stationary energy consumption scenarios.
 |
Figure 3 Real-time electricity consumption data of five residential buildings. |
Data preprocessing is crucial before developing a deep learning model, though it can significantly affect prediction accuracy. The electricity consumption dataset may contain missing values. The following data preprocessing steps are applied to the electricity dataset:
-
The set of missing values is interpolated using the mean of the previous year’s data values for the same time interval. Linear interpolation is adopted to estimate the missing values in the time-series data that calculates the unknown values in the same increasing or decreasing order as the previous values.
-
The electricity consumption measurements need to be normalized on the same scale. The Min–Max scalar is applied for feature scaling of electricity load data. The scalar converts the electricity measurements column into the range of 0, and 1 [35]. For the electricity load feature
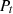 , the new normalized feature
, the new normalized feature 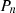 is given by equation (1):
is given by equation (1):
The geographical and semitropical location of the state is the reason behind substantial temperature variation between different months. In the following section, seasonal clusters have been extracted for real-time residential buildings.
3.2 Data clustering
In order to perform accurate and efficient forecasting of electricity consumption patterns, cluster analysis would be helpful to provide a deep understanding of usage by examining the seasonal variation. For the given real-world scenarios, the prevailing climatic conditions are characterized by intense heat and extremely cold temperatures. As a result, the degree of variation and fluctuation can be observed in the electricity consumption of households. The present work employs a hierarchical clustering technique called BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies) [36] to fetch seasonal electricity consumption patterns. BIRCH can handle a large amount of historical energy consumption data and is suitable when data points are not uniformly distributed [37]. In order to identify the overall trends and patterns of data, it attempts to determine the dense and sparse regions. Using BIRCH, the individual data points are not evaluated, but a dense region of data points is treated as a single cluster.
BIRCH involves grouping the data points into compact summaries called Clustering Features (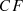 ), which are further grouped into even more compact clusters known as
), which are further grouped into even more compact clusters known as 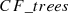 [38].
[38]. 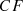 is a vector of three values with the values
is a vector of three values with the values 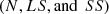 , where N denotes the time series length, LS is the linear sum, and SS is the squared sum of the data points.
, where N denotes the time series length, LS is the linear sum, and SS is the squared sum of the data points.
Algorithm 1 is used to create the seasonal clusters using a real-time electricity consumption dataset. Firstly, the threshold value is initialized, and input data is scanned. The algorithm begins with a default threshold value, screens the data, and puts data points to the tree. The initial 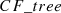 is constructed, but if it runs out of memory, the CF_tree is rebuilt by increasing the threshold value. If the number of data points is within a certain range, group dense sub-clusters into larger ones, resulting in a smaller CF_tree. Two disjoint adjacent time series are merged by adding clustering features
is constructed, but if it runs out of memory, the CF_tree is rebuilt by increasing the threshold value. If the number of data points is within a certain range, group dense sub-clusters into larger ones, resulting in a smaller CF_tree. Two disjoint adjacent time series are merged by adding clustering features 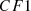 and
and 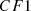 . The adjacent cluster merging is repeated until it reaches the end of the time-series data. Eventually, when the clustering ends and the sub-sequence
. The adjacent cluster merging is repeated until it reaches the end of the time-series data. Eventually, when the clustering ends and the sub-sequence  is merged into cluster vector
is merged into cluster vector 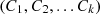 where k is the number of clusters and
where k is the number of clusters and 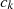 is the newly created cluster. Hence, the output of the clustering algorithm is further used for seasonal analysis and trend analysis.
is the newly created cluster. Hence, the output of the clustering algorithm is further used for seasonal analysis and trend analysis.
Input: Time series dataset (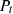 as
as 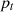 ) and C = data points in each cluster, K = Max clusters
) and C = data points in each cluster, K = Max clusters
Output: Season-wise energy clusters
Begin
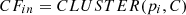
if 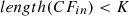 then
then
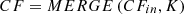
else
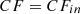
else if
End
function cluster 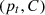
CFin = ϕ, i = 1, j = 1
if 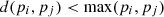 then
then

else
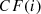 =
=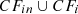
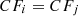
else if 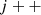
end function
function merge(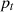 ,
, 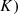
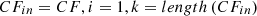
while 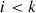 do
do
calculate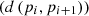
end while
while  do
do

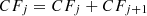
Delete 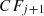 from
from 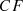
update 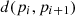 and
and 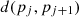
end while
end function
3.3 Decomposition and reconstruction
The real-time electricity consumption data exhibits complex seasonal variations, and therefore, it is necessary to extract essential features prior to modeling. The present work applies data decomposition on the electricity time-series data using I-CEEMDAN. The objective is to effectively capture the temporal dynamics and seasonality inherent in the data [31]. I-CEEMDAN has addressed EEMD’s mixing mode issue and reduced computation time to a certain level, including white noise adaptively during decomposition. The original non-stationary time series energy dataset is divided into stationary components by I-CEEMDAN, known as IMFs, to enhance prediction accuracy. I-CEEMDAN divides the original time series signals using the estimated local means of time series plus noise signals. Further, it finds the difference between the average local means and current residues to minimize the residual noise. The time-series decomposition problem is described using the following steps:
- 1.
The electricity time series is represented as P(t) where t is the time-stamp.
- 2.
Create the different ensemble series and for each ensemble series P(t), add white noise w i using equation (2)
- 3.
For each
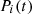 apply Empirical Mode Decomposition into IMFs using (3) and the residual noise using equation (4):
apply Empirical Mode Decomposition into IMFs using (3) and the residual noise using equation (4):
- 4.
Step 3 is repeated for
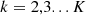 until the residual r(t) contain non-stationary series. The final residual R(t) can be obtained by equation (5):
until the residual r(t) contain non-stationary series. The final residual R(t) can be obtained by equation (5):
To ensure the completeness of the decomposition method, the original data is reconstructed using the following equation (6)
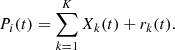 (6)
(6)
The decomposition performed by the I-CEEMDAN method obtained 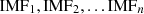 mode components. The first mode component IMF1 contains error, irregularity, and redundancy that must be addressed for accurate predictive performance. Therefore, this paper adopted the autoencoder model to train and reconstruct the original sub-signal. Autoencoders are a kind of neural network developed to map the input signal data into latent space representation and reconstruct the original input signal from encoded data [39]. The architecture of the autoencoder is split into two parts, as shown in Figure 2, namely the encoder and decoder network:
mode components. The first mode component IMF1 contains error, irregularity, and redundancy that must be addressed for accurate predictive performance. Therefore, this paper adopted the autoencoder model to train and reconstruct the original sub-signal. Autoencoders are a kind of neural network developed to map the input signal data into latent space representation and reconstruct the original input signal from encoded data [39]. The architecture of the autoencoder is split into two parts, as shown in Figure 2, namely the encoder and decoder network:
-
Encoder: It is trained to encode the IMFs into lower dimensional latent space representation, given by:
-
Decoder: It is trained to reconstruct the original input from the encoded representation, given by:
where we, wd are weight values, b1, b2 are bias values for encoder and decoder networks respectively. The autoencoder model training extracts and reconstructs the mode components generated by the I-CEEMDAN algorithm. During the encoding–decoding process, the redundant features, noise, and irregular patterns have been removed.
3.4 Data prediction
To predict the electricity consumption of residential buildings, a neural network model LSTM is adopted as it can effectively deal with time-series data. The LSTM model is extensively employed in the domain of time-series prediction problems since it can learn from preceding time steps [21]. It is capable of modeling long-term sequential dependencies between the time-series data using the concept of gates into the cell states [14]. The architecture of LSTM consists of four neural network components: forget gate, input gate, cell, and output gate [40]. In the first step, it calculates the activation value of the forget gate ft using input Pt to determine the irrelevant information and remove the information that is no longer useful in the previous cell state 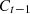 . It is represented by equation (9) given below [40]:
. It is represented by equation (9) given below [40]: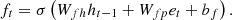 (9)
(9)
To update and produce an updated cell state Ct, a vector of new candidate values 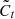 is used. The cell is responsible for retaining the information for a long time, and the formula is given below in equations (10) and (11) [14, 40]:
is used. The cell is responsible for retaining the information for a long time, and the formula is given below in equations (10) and (11) [14, 40]: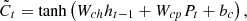 (10)
(10)
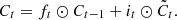 (11)
(11)
The input gate it decides which information should be entered into the memory cell at the timestamp i, and its equation is given by equation (13). The updated hidden state is obtained by equation (12) [40]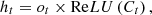 (12)
(12)
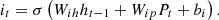 (13)
(13)
The output gate ot manages the output values of the cell state and contains a sigmoid layer to filter the output. Further, the updated cell state Ct is forwarded to tanh, which normalizes the values between (−1) and (1). The final output of the cell has been obtained by multiplying the output and new cell state that is given by equation (14) below [14]![$$ {o}_t=\sigma \left({W}_{{oh}}\left[\overrightarrow{{h}_t},\overleftarrow{{h}_t}\right]+{b}_o\right). $$](/articles/stet/full_html/2024/01/stet20230153/stet20230153-eq58.gif) (14)
(14)
In the above equations, Pt depicts the input value while ot is the output value at the current time t. The weight matrices (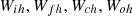 ) represent input gate, forget gate, cell state, and output gate, respectively. Whereas, (
) represent input gate, forget gate, cell state, and output gate, respectively. Whereas, (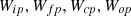 ) denotes the input weight matrices and (
) denotes the input weight matrices and (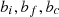 ) represents the corresponding bias values.
) represents the corresponding bias values.
The procedure to implement the proposed hybrid prediction algorithm has been stated in Algorithm 2. Using the Algorithm, LSTM models have been trained for reconstructed electricity time-series produced by I-CEEMDAN and autoencoder model. The general approach is to build an LSTM model using a one-dimensional array (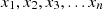 ) to predict the data points. However, this input format is not valid for predicting the time series data. Accordingly, input data has been transformed into a three-dimensional input matrix (P,T,D) where P indicates the input data points, T denotes the series length, and
) to predict the data points. However, this input format is not valid for predicting the time series data. Accordingly, input data has been transformed into a three-dimensional input matrix (P,T,D) where P indicates the input data points, T denotes the series length, and 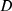 indicates input features. The three-dimensional dataset
indicates input features. The three-dimensional dataset 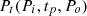 has been prepared where
has been prepared where 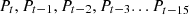 where Pi denotes the number of input samples, tp indicates the historical timestamp and Po depicts the prediction output. Certainly, the lagged parameters play a vital role in historical datasets with seasonality to get accurate predictions. Apart from this, the hyperparameters should be selected very carefully because these can impact the performance of the LSTM model.
where Pi denotes the number of input samples, tp indicates the historical timestamp and Po depicts the prediction output. Certainly, the lagged parameters play a vital role in historical datasets with seasonality to get accurate predictions. Apart from this, the hyperparameters should be selected very carefully because these can impact the performance of the LSTM model.
-
Hyper-parameters selection: The LSTM model consists of several hyperparameters and the appropriate values are determined such as two LSTM layers having 64 neuron units, a dense layer, 100 epochs, 64 batch size, and tanh as activation function. However, these hyperparameters are chosen while training the LSTM model iteratively until it gets accurate predictions. The hidden neuron values 16, 32, and 64 were tested, but it concluded that 64 neuron units gave better results. An adaptive learning-based optimization algorithm, ADAM optimizer [41], is used to train the proposed prediction model with a 0.01 learning rate. ADAM optimizer has fast computation time and performs better than other optimizers.
-
Sliding window size: The optimal input/output window size must be chosen to achieve precise predictions. The input and output window size is based on the prediction horizon. In the proposed work, input_window size is 15, and output_window size is 1; although different input_window sizes such as 7, 10, and 30 have been verified, optimal results have been obtained with 15.
Input: Time series reconstructed data provided by autoencoder 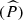
Output: Electricity demand predictions [1]
1: Initialize LSTM hyperparameters
2: apply sliding_window approach
3: 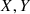 = partition_data(train_x,window_size)
= partition_data(train_x,window_size)
4: split into train and test sets
5: for 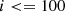 do
do
6: train LSTM model
7: Calculate fitness_score  MAE
MAE
8: end for
9: model.predict(test_x)
10: Calculate loss = MAE
The proposed work applied sliding window approach [42] that provides the previous timestamp values to the LSTM model by splitting the time series data (size N) into (N − out_window − in_window) subsequences of length (out_window + in_window). The sliding window moves over the entire dataset subsequently, and this process of iterating over input_window and out_window goes on until it reaches the last window.
3.5 Performance metrics
The proposed multi-step prediction model is assessed using state-of-the-art statistical measures such as Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE). The performance metrics are computed using the following equations (15)–(17):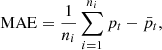 (15)
(15)
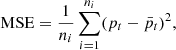 (16)
(16)
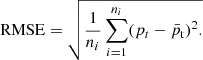 (17)where ni is the number of power measurements, pt is the actual values in the test set and
(17)where ni is the number of power measurements, pt is the actual values in the test set and 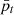 is the predicted electricity of residential buildings.
is the predicted electricity of residential buildings.
4 Experimental results
The proposed work has been implemented on a real-time electricity dataset provided by PSPCL, Punjab. The electricity consumption dataset is stored in a Comma-Separated-Value (CSV) file format. The training and testing experiments are performed on an Intel Core i5 with 16 GB RAM and Windows 10 operating system.
4.1 Cluster analysis
To achieve precise and realistic predictions of energy consumption trends, data clustering has been performed to extract more detailed and specific information pertaining to electricity usage. The aim of cluster analysis is to provide a better understanding of data during different days, weeks, and months of the year. Data clustering has explored seasonal variation in electricity consumption due to changing weather conditions throughout the year. The results and findings of the proposed data clustering approach have been discussed below.
-
Seasonal analysis: The data clustering phase extracted three (summer, rain, and winter) weather clusters. The cluster distribution throughout the year is shown in Figure 4. It represents that cluster 1 (winter season cluster) is mainly distributed in October end, November, December, January, February, and the beginning of March. Meanwhile, cluster 2 (summer season cluster) is distributed between early March, April, May, and June. However, cluster 3 (rainy season cluster) is spread across July, August, September, and mid-October. This analysis signifies that the weather conditions are heterogeneous throughout the year, influencing energy consumption predictions.

Figure 4 Season-wise cluster analysis of electricity consumption in residential buildings where C1-cluster 1, C2-cluster 2 and C3-cluster 3.
-
Cluster-wise trend analysis: The output of the clustering algorithm has been used to depict the energy consumption patterns within each cluster. This paper considers individual residential buildings for trend analysis of electricity usage during different months of the year, as shown in Figure 5. It is evident from Figure 5 that the energy consumption trend varies according to changing weather conditions throughout the year.

Figure 5 Cluster analysis of electricity consumption patterns in residential buildings during different seasons of the year.
In the subsequent stage, cluster analysis results were used to extract different frequency components from electrical consumption data.
4.2 Decomposition and reconstruction analysis
After performing seasonal and cluster analysis, the next step is to decompose the electricity time series data into several sub-signals and residuals using the I-CEEMDAN algorithm. Data decomposition revealed the underlying patterns and trends in load time series data as shown in Figure 2. It separated the seasonal patterns, trends, and residual noise, which is essential for prediction accuracy. The decomposition algorithm has been implemented using the pyEMD [43] package. The data decomposition process obtained seven sub-signals 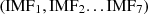 , and an example decomposition is shown in Figure 2, arranged from highest to lowest frequency range. The first mode component IMF1 shows highly irregular patterns, while IMF2 to IMF8 represents periodic patterns, and the last IMF9 depicts the general trend of energy consumption. Next, the autoencoder model is built and trained to reconstruct the original signal for the extracted mode components. The autoencoder model merges the meaningful sub-signals and obtains a noise-free series of electricity consumption features. The aforementioned process is repeated for five residential buildings’ electricity consumption datasets.
, and an example decomposition is shown in Figure 2, arranged from highest to lowest frequency range. The first mode component IMF1 shows highly irregular patterns, while IMF2 to IMF8 represents periodic patterns, and the last IMF9 depicts the general trend of energy consumption. Next, the autoencoder model is built and trained to reconstruct the original signal for the extracted mode components. The autoencoder model merges the meaningful sub-signals and obtains a noise-free series of electricity consumption features. The aforementioned process is repeated for five residential buildings’ electricity consumption datasets.
4.3 Prediction results and analysis
The objective of the present work is to predict the daily electricity consumption of residential buildings. LSTM-based prediction model has been built and trained for the given decomposed and seasonal data. To demonstrate the effectiveness of the multi-step prediction approach, four other state-of-the-art models have been trained to predict the electricity consumption of individual residential buildings. The widely used statistical measures such as MAE, RMSE, and MSE have been used to verify the prediction performance. Figure 6 visually represents the predicted electricity consumption in individual residential buildings where the x-axis and y-axis denote the number of data points and electricity consumption values, respectively. The orange line shows estimated electricity demand, whereas the blue line indicates actual consumption. Table 1 presents the prediction performance of five models on five residential buildings’ datasets. The experimental results show that the proposed I-CEEMDAN-LSTM approach obtained a minimum MAE of 0.114 kWh, while the MAE of SVR, RF, RNN, and LSTM models are 0.195 kWh, 0.162 kWh, 0.137 kWh, and 0.131 kWh respectively while estimating the electricity demand of RB-4. For other residential buildings, like RB-1, and RB-5, the proposed model attained accurate electricity load predictions and achieved the MAE of 0.115 kWh. For residential building (RB-2), the prediction error is slightly higher than the other buildings because data points are more densely concentrated for some days and also show sudden fluctuations, as shown in Figure 3. The comparative analysis shows that the proposed multi-step prediction approach outperformed in terms of MAE, MSE, and RMSE predicting energy consumption in residential buildings. The accuracy of the proposed approach has been evaluated with state-of-the-art prediction models using the percentage improvement formula. The following equations have been used to calculate the percentage improvement of MAE, RMSE, and MSE between any two prediction models: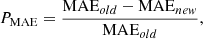 (18)
(18)
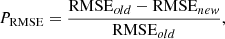 (19)
(19)
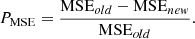 (20)
(20)
 |
Figure 6 Predicted and actual electricity consumption of residential buildings using hybrid improved CEEMDAN-LSTM approach. |
Performance of proposed I-CEEMDAN-LSTM model using real-world electricity dataset in Punjab, India (where RB is Residential Building).
Compared to other state-of-the-art models, the percentage error improvement attained by the proposed I-CEEMDAN-LSTM model has been presented in Table 2, which is discussed in the following subsection.
Improved percentage results of the proposed I-CEEMDAN-LSTM model compared to the state-of-the-art model in terms of MAE, RMSE, and MSE values.
4.4 Discussion
The performance improvement of the proposed multi-step model is also compared with three state-of-the-art prediction models, namely, SVR, RF, and RNN. The following inferences can be drawn from the prediction results obtained by the proposed I-CEEMDAN-LSTM approach, and other state-of-the-models have been listed in Tables 1 and 2.
-
Electricity consumption load exhibits fluctuating and non-linear behavior, making it challenging to predict using a single machine learning-based model accurately. Therefore, the proposed hybrid prediction approach outperformed the given real-time scenarios.
-
The influence of seasonal variation on electricity consumption and cluster analysis indicates that energy consumption positively correlates with changing climatic conditions and possesses heterogeneous consumption patterns. The RNN model performed better, achieving the lowest MAE (0.137 kWh) compared to the SVR model (MAE: 0.192 kWh) and RF model (0.162 kWh). The decomposition and reconstruction model incorporation improved the prediction accuracy of the LSTM model compared to direct prediction approaches. The aim of the comparison between LSTM and the hybrid I-CEEMDAN-LSTM model is to depict the effectiveness of the proposed I-CEEMDAN-LSTM model. The proposed model attained excellent predictive performance on MAE, RMSE, and MSE during the testing phase, and the lowest values are 0.114 kWh, 0.141 kWh, and 0.125 kWh, respectively. Therefore, the proposed multi-step prediction model could be used as a prediction and analysis tool for residential buildings.
-
The incorporation of historical dependencies and seasonal variations allowed the LSTM model to memorize patterns across previous time steps. Therefore, the proposed approach attained better accuracy than the SVR model, with an improvement in the MAE percentage of 56.85% for RB-3. Compared to the RF model, MAE percentage improvement is 51.88% for RB-5; further, compared to the RNN model, the MAE percentage improvement is 43.19% for RB-2. The results indicate that the proposed multi-step model has achieved a lower error rate (MAE: 0.114 kWh) in comparison to the work conducted by Karijadi et al. [14]. The authors [14] utilized a hybrid RF-LSTM model based on CEEMDAN to predict the electricity demand of five buildings inside a University campus, and the reported MAE values were 1.369 kWh, 1.014 kWh, 0.57 kWh, 0.43 kWh, and 0.299 kWh, respectively.
4.5 Implications and limitations
Real-time residential buildings’ electricity consumption data has been exploited to generate the historical dataset for the proposed multi-step prediction model. The electricity consumption in real-time residential buildings shows non-linear and non-stationary trends. Once the proposed prediction model has been well-trained and tested, adopting the real-time dataset, it could be deployed by the electricity distribution sector as a prediction and analytical tool. It would also be helpful to raise awareness among consumers through daily energy consumption patterns, and the consumer can link their present usage with the future cost. Incorporating cluster analysis and data decomposition provided significant findings in real-world scenarios. The effectiveness of the proposed work relies significantly on the quantity and quality of the dataset. The quality of real-time data should be evaluated to ensure its completeness and consistency. The benchmark or simulated dataset taken from reliable sources can be utilized where real-time data collection is not feasible.
5 Conclusion
This paper proposed a deep learning-based multi-step approach to predict electricity consumption in the residential sector. In the first step, seasonal trend analysis has been performed to obtain season-based temporal data. The second step applied an improved CEEMDAN method to decompose the electricity consumption time series into IMFs, which removes irregular patterns, noise, and non-stationary components. Then, an autoencoder model has been implemented to reconstruct the original series using IMFs. Subsequently, the LSTM network model has been developed and trained by considering the historical, seasonal, and temporal data dependencies. The effectiveness of the proposed approach has been verified using real-time residential buildings in Punjab, India. The experimental results revealed that the proposed hybrid I-CEEMDAN-LSTM approach supports improved prediction error (MAE: 0.114) compared to the existing RF-LSTM model based on the CEEMDAN method (MAE: 0.299). Further, the proposed prediction model could also be used for other time series data that exhibit non-linear and non-stationary characteristics. The influential factors, such as building design features, time-based pricing, operational hours, and user behavior, show potential for future research and analysis.
Conflict of interest
The authors declare no conflict of interest in preparing this article.
Author contributions
All the authors made substantial contributions in preparing this manuscript, including the conception, design, data analysis, and article drafting.
Data availability statement
The electricity consumption dataset that supports the findings of this research work is available at https://sites.google.com/thapar.edu/electricity-dataset/home.
Funding
The authors have no financial or proprietary interests in any material discussed in this article.
References
- IEA (2022) World energy outlook, International Energy Agency. Report https://www.iea.org/reports/world-energy-outlook-2022. [Google Scholar]
- Tiwari S., Jain A., Ahmed N.M.O.S., Alkwai L.M., Dafhalla A.K.Y., Hamad S.A.S. (2022) Machine learning-based model for prediction of power consumption in smart grid-smart way towards smart city, Expert Syst. 39, 5, e12832. [CrossRef] [Google Scholar]
- Chou J.-S., Tran D.-S. (2018) Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders, Energy 165, 709–726. [CrossRef] [Google Scholar]
- Goudarzi S., Anisi M.H., Kama N., Doctor F., Soleymani S.A., Sangaiah A.K. (2019) Predictive modelling of building energy consumption based on a hybrid nature-inspired optimization algorithm, Energy Build. 196, 83–93. [CrossRef] [Google Scholar]
- Wang Z., Wang Y., Zeng R., Srinivasan R.S., Ahrentzen S. (2018) Random forest based hourly building energy prediction, Energy Build. 171, 11–25. [CrossRef] [Google Scholar]
- Ferrández-Pastor F.-J., Mora H., Jimeno-Morenilla A., Volckaert B. (2018) Deployment of IoT edge and fog computing technologies to develop smart building services, Sustainability 10, 11, 3832–3855. [CrossRef] [Google Scholar]
- Bourhnane S., Abid M.R., Lghoul R., Zine-Dine K., Elkamoun N., Benhaddou D. (2020) Machine learning for energy consumption prediction and scheduling in smart buildings, SN Appl. Sci. 2, 2, 297–307. [CrossRef] [Google Scholar]
- Amarasinghe K., Marino D.L., Manic M. (2017) Deep neural networks for energy load forecasting, in 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), IEEE, pp. 1483–1488. [CrossRef] [Google Scholar]
- Gardner M.W., Dorling S.R. (1998) Artificial neural networks (the multilayer perceptron) – a review of applications in the atmospheric sciences, Atmos. Environ. 32, 14–15, 2627–2636. [CrossRef] [Google Scholar]
- Jain R.K., Smith K.M., Culligan P.J., Taylor J.E. (2014) Forecasting energy consumption of multi-family residential buildings using support vector regression: investigating the impact of temporal and spatial monitoring granularity on performance accuracy, Appl. Energy 123, 168–178. [CrossRef] [Google Scholar]
- Sajjad M., Khan Z.A., Ullah A., Hussain T., Ullah W., Lee M.Y., Baik S.W. (2020) A novel CNN-GRU-based hybrid approach for short-term residential load forecasting, IEEE Access 8, 143759–143768. [CrossRef] [Google Scholar]
- Gaur M., Makonin S., Bajić I.V., Majumdar A. (2019) Performance evaluation of techniques for identifying abnormal energy consumption in buildings, IEEE Access 7, 62721–62733. [CrossRef] [Google Scholar]
- Bedi J., Toshniwal D. (2018) Empirical mode decomposition based deep learning for electricity demand forecasting, IEEE Access 6, 49144–49156. [CrossRef] [Google Scholar]
- Karijadi I., Chou S.-Y. (2022) A hybrid RF-LSTM based on CEEMDAN for improving the accuracy of building energy consumption prediction, Energy Build. 259, 111908. [CrossRef] [Google Scholar]
- Chai S., Zhang Z., Zhang Z. (2021) Carbon price prediction for China’s ETS pilots using variational mode decomposition and optimized extreme learning machine, Ann. Oper. Res. 1–22. [Google Scholar]
- Kaur S., Bala A., Parashar A. (2022) Intelligent energy aware approaches for residential buildings: state-of-the-art review and future directions, Cluster Comput. 16, 1–18. [Google Scholar]
- Kaur J., Bala A. (2019) A hybrid energy management approach for home appliances using climatic forecasting, in Building Simulation, Vol. 12, Springer, pp. 1033–1045. [CrossRef] [Google Scholar]
- Chinthavali S., Tansakul V., Lee S., Tabassum A., Munk J., Jakowski J., Starke M., Kuruganti T., Buckberry H., Leverette J. (2019) Quantification of energy cost savings through optimization and control of appliances within smart neighborhood homes, in Proceedings of the 1st ACM International Workshop on Urban Building Energy Sensing, Controls, Big Data Analysis, and Visualization, pp. 59–68. [Google Scholar]
- Verma M., Bhambri S., Buduru A.B. (2019) Making smart homes smarter: optimizing energy consumption with human in the loop. arXiv preprint arXiv:1912.03298. [Google Scholar]
- Luo X.J., Oyedele L.O., Ajayi A.O., Akinade O.O., Owolabi H.A., Ahmed A. (2020) Feature extraction and genetic algorithm enhanced adaptive deep neural network for energy consumption prediction in buildings, Renewable and Sustainable Energy Reviews 131, 109980. [CrossRef] [Google Scholar]
- Bedi J., Toshniwal D. (2020) Energy load time-series forecast using decomposition and autoencoder integrated memory network, Appl. Soft Comput. 93, 106390. [CrossRef] [Google Scholar]
- Wahid F., Ghazali R., Fayaz M., Shah A.S. (2017) A simple and easy approach for home appliances energy consumption prediction in residential buildings using machine learning techniques, J. Appl. Environ. Biol. Sci 7, 3, 108–119. [Google Scholar]
- Huber P., Gerber M., Rumsch A., Paice A. (2018) Prediction of domestic appliances usage based on electrical consumption, Energy Inform. 1, 1, 265–271. [Google Scholar]
- Mohammadi M., Talebpour F., Safaee E., Ghadimi N., Abedinia O. (2018) Small-scale building load forecast based on hybrid forecast engine, Neural Process. Lett. 48, 1, 329–351. [CrossRef] [Google Scholar]
- Fan C., Sun Y., Zhao Y., Song M., Wang J. (2019) Deep learning-based feature engineering methods for improved building energy prediction, Appl. Energy 240, 35–45. [CrossRef] [Google Scholar]
- Kumari S., Kumar N., Rana P.S. (2021) Big data analytics for energy consumption prediction in smart grid using genetic algorithm and long short term memory, Comput. Inform. 40, 1, 29–56. [CrossRef] [MathSciNet] [Google Scholar]
- Kaur S., Bala A., Parashar A. (2023) GA-BiLSTM: an intelligent energy prediction and optimization approach for individual home appliances, Evol. Syst. 1–15. [Google Scholar]
- Liu D., Yang Q., Yang F. (2020) Predicting building energy consumption by time series model based on machine learning and empirical mode decomposition, in 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), IEEE, pp. 145–150. [CrossRef] [Google Scholar]
- An N., Zhao W., Wang J., Shang D., Zhao E. (2013) Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting, Energy 49, 279–288. [CrossRef] [Google Scholar]
- Zhaohua W., Huang N.E. (2009) Ensemble empirical mode decomposition: a noise-assisted data analysis method, Adv. Adapt. Data Anal. 1, 1, 1–41. [CrossRef] [Google Scholar]
- Colominas M.A., Schlotthauer G., Torres M.E. (2014) Improved complete ensemble EMD: a suitable tool for biomedical signal processing, Biomed.l Signal Process. Control 14, 19–29. [CrossRef] [Google Scholar]
- Torabi M., Hashemi S., Saybani M.R., Shamshirband S., Mosavi A. (2019) A hybrid clustering and classification technique for forecasting short-term energy consumption, Environ. Prog. Sustain. Energy 38, 1, 66–76. [CrossRef] [Google Scholar]
- Hafeez G., Alimgeer K.S., Khan I. (2020) Electric load forecasting based on deep learning and optimized by Heuristic algorithm in smart grid, Appl. Energy 269, 114915–114933. [CrossRef] [Google Scholar]
- Kaur S., Bala A., Parashar A. (2023) Electricity consumption dataset. https://sites.google.com/thapar.edu/electricity-dataset/home. [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M., Duchesnay E. (2011) Scikit-learn: machine learning in Python, J. Mach. Learn. Res. 12, 2825–2830. [MathSciNet] [Google Scholar]
- Yu T., Liu Y., Li Z. (2010) Online segmentation algorithm for time series based on BIRCH clustering features, in 2010 International Conference on Computational Intelligence and Security, IEEE, pp. 55–59. [Google Scholar]
- Zhang T., Ramakrishnan R., Livny M. (1996) BIRCH: an efficient data clustering method for very large databases, ACM SIGMOD Rec. 25, 2, 103–114. [CrossRef] [Google Scholar]
- Nhon VLQ, Anh DT (2012) A birch-based clustering method for large time series databases, in New Frontiers in Applied Data Mining: PAKDD 2011 International Workshops, Shenzhen, China, May 24–27, 2011, Revised Selected Papers 15, Springer, pp. 148–159. [Google Scholar]
- Sheu M.-H., Jhang Y.-S., Chang Y.-C., Wang S.-T., Chang C.-Y., Lai S.-C. (2022) Lightweight denoising autoencoder design for noise removal in electrocardiography, IEEE Access 10, 98104–98116. [CrossRef] [Google Scholar]
- Yang M., Wang J. (2022) Adaptability of financial time series prediction based on BiLSTM, Procedia Comput. Sci. 199, 18–25. [CrossRef] [Google Scholar]
- Kingma D.P., Ba J. (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- Norwawi N.M. (2021) Sliding window time series forecasting with multilayer perceptron and multiregression of COVID-19 outbreak in Malaysia, in Data Science for COVID-19, Elsevier, pp. 547–564. [Google Scholar]
- Laszuk D. (2017) Python implementation of empirical mode decomposition algorithm. https://github.com/laszukdawid/PyEMD. [Google Scholar]
- IEA (2021) India energy outlook, IEA, Paris, International Energy Agency. Report https://www.iea.org/reports/india-energy-outlook-2021. [Google Scholar]
All Tables
Performance of proposed I-CEEMDAN-LSTM model using real-world electricity dataset in Punjab, India (where RB is Residential Building).
Improved percentage results of the proposed I-CEEMDAN-LSTM model compared to the state-of-the-art model in terms of MAE, RMSE, and MSE values.
All Figures
 |
Figure 1 Sector-wise energy consumption in India (IEA report on India Energy Outlook, 2022) [44]. |
| In the text | |
 |
Figure 2 Proposed electricity consumption forecasting approach for residential buildings. |
| In the text | |
 |
Figure 3 Real-time electricity consumption data of five residential buildings. |
| In the text | |
 |
Figure 4 Season-wise cluster analysis of electricity consumption in residential buildings where C1-cluster 1, C2-cluster 2 and C3-cluster 3. |
| In the text | |
 |
Figure 5 Cluster analysis of electricity consumption patterns in residential buildings during different seasons of the year. |
| In the text | |
 |
Figure 6 Predicted and actual electricity consumption of residential buildings using hybrid improved CEEMDAN-LSTM approach. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.