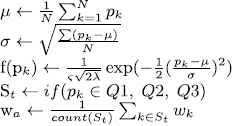| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Emerging Advances in Hybrid Renewable Energy Systems and Integration
|
|
|---|---|---|
| Article Number | 85 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.2516/stet/2024060 | |
| Published online | 23 October 2024 | |
Regular Article
Enhancing energy consumption prediction in smart homes: a convergence-aware federated transfer learning approach
1
Department of Electronic Engineering, Kyung Hee University, Yongin 17104, Republic of Korea
2
Department of Computer Engineering, Jeju National University, Jeju 63243, Republic of Korea
3
Faculty of Computing and IT, Sohar University, Sohar 311, Oman
4
Department of Mechanical Engineering, College of Engineering, Alfaisal University, Takhassusi St., Al Maather Road, P.O. Box 50927, Riyadh 11533, Saudi Arabia
5
Department of Information Technology, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia
* Corresponding author: geatteiaallah@pnu.edu.sa
Received:
16
June
2024
Accepted:
24
July
2024
Achieving accurate energy consumption prediction can be challenging, particularly in residential buildings, which experience highly variable consumption behavior due to changes in occupants and the construction of new buildings. This variability, combined with the potential for privacy breaches through conventional data collection methods, underscores the need for novel approaches to energy consumption forecasting. The proposed study suggests a new approach to predict energy consumption, utilizing Federated Learning (FL) to train a global model while ensuring local data privacy and transferring knowledge from information-rich to information-poor buildings. The proposed method learns the transferable knowledge from the source building without any privacy leakage and utilizes it for target buildings. Since the performance of the global model could be negatively affected by some participating nodes with poor performance due to noisy or limited data, we propose a client selection strategy on the server based on the normal distribution for choosing the best possible participants for the global model. Our method enables clients to participate selectively in the aggregation procedure to avoid model divergence due to poor performance. The proposed model is evaluated and conducts in-depth analyses of energy consumption patterns. We validate the performance by comparing its Mean Absolute Error (MAE), Mean Square Error (MSE), and R2 values to those of existing traditional and ensemble models. Our findings indicate that the proposed FL-based model with selective client participation outperforms its counterpart methods regarding predictive accuracy and robustness. The source code is available on GitHub (https://github.com/atifrizwan1/TFL-PP).
Key words: Federated Learning / Energy consumption forecasting / Energy management / Smart buildings / Partial client participation
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The generation of electricity is a significant contributor to greenhouse gas emissions, constituting approximately two-thirds of total emissions, as stated by [1]. Global organizations are striving to mitigate the negative impact of carbon emissions by establishing aspiring goals; for instance, the European Union (EU) aims to minimize 40% of the carbon emissions by 2030 to achieve 27% higher energy efficiency than before [2]. However, energy demand is rising, making energy management a critical aspect in mitigating environmental effects and keeping up with rising energy needs [3]. The process of load forecasting is crucial to energy management because it allows for more accurate design of power infrastructure, scheduling of electricity generation, and maintenance of a stable demand/supply ratio. Additionally, the monetary gains from accurate load forecasting can be substantial; for instance, Xcel Energy saved 2.5 M$ by decreasing forecasting error from 15.7% to 12.2% [3].
Across the globe, smart meters are installed to enhance energy efficiency and offer consumers greater control over their energy usage. The combination of advanced metering infrastructure and the extensive deployment of smart meters has enabled utilities to monitor energy consumption on both broad temporal and spatial scales. For instance, nearly 15 million smart meters are currently used in the United Kingdom’s residential sector alone [4]. The substantial volume of data generated by these smart meters has unveiled previously unattainable insights into energy consumption patterns and facilitated accurate load forecasting at the individual household level.
To facilitate the training of a Machine Learning (ML) model for accurate load forecasting, sensor-based techniques utilize historical load data obtained from smart meters, often combined with meteorological information. Typically, the data collected from these smart meters is uploaded to a centralized server for storage and utilization in ML model training. These centralized training approaches can be categorized broadly into two types: In the first approach, distinct models are trained using smart-meter data from individual residential dwellings, resulting in distinct energy consumption forecasts for each household. In the second approach, a singular model is trained on the central server using data gathered from multiple smart meters, yielding aggregated consumption forecasts [5]. Both of these centralized training methods yield favorable outcomes; however, they are computationally intensive, necessitating the transfer of all data to a central hub, which could potentially strain network resources [6]. Additionally, centralized training is not aligned with the stringent guidelines of the EU General Data Protection Regulation (GDPR) [7]. This is due to the requirement of sharing local data with the central server, thereby raising concerns related to security and privacy.
Federated Learning (FL), an emerging paradigm, can provide a solution to these problems by collaboratively training a ML model without the need to share or store the data in a centralized location [8]. In FL, the edge devices collaborate to improve a centralized ML model by receiving a global model update of the centralized model and subsequently training it on their own private data. Then, the local model parameters are shared with the aggregator server, where local model parameters are aggregated into a single global model without sharing privacy-sensitive data. When compared to traditional, expensive centralized ML systems, FL is a major paradigm shift towards distributed ML exploiting a wide variety of decentralized processing resources. Meanwhile, the learning takes place locally on each device, privacy is preserved, and network resource utilization is improved [9] since only model updates are exchanged rather than the original data.
Federated learning presumes that a global model can discern client-level patterns. In load forecasting, this involves a global model generating electric load forecasts for individual consumers. However, given the high variability in consumer consumption patterns, a singular global model may not capture the nuances of each smart meter’s consumption forecast accurately, leading to potential inaccuracies. To enhance the accuracy and robustness of the global model, this study introduces a normal distribution-based client selection method. This approach ensures the inclusion of the most suitable participants in the global model, mitigating model divergence caused by nodes with noisy or limited data. By selectively involving clients in the aggregation process, this method addresses a significant FL challenge: data heterogeneity across clients.
Previous studies have explored FL for knowledge transfer but have not adequately considered the quality of the transferred knowledge. There is a risk that source clients might include malicious entities, potentially compromising the target models and diverging the globally trained model. Our proposed study addresses this by first applying a normal distribution to select high-quality models for the global model, subsequently transferring knowledge to target clients. This dual-step approach ensures both the integrity and the efficacy of knowledge transfer in FL environments.
To address this challenge, we proposed FL framework for energy consumption prediction using data provided by a research institute. We introduce Fed-LSTM and Fed-DNN as our learning models. Our study leverages LSTM networks and DNNs due to their proven ability to generalize across diverse data distributions, which is essential for accurate energy consumption forecasting. The robustness of these models in capturing complex temporal patterns ensures that our findings, though based on a dataset of 11 buildings, have broader applicability. This methodology supports the scalability of our research, making it promising for future expansion to include a more varied set of buildings and thereby enhancing the generalizability of our results. Additionally, LSTM and DNN models are widely adopted in the energy forecasting domain for their capacity to map spatial and temporal correlations in time-series data.
The core contributions of the proposed work are as follows:
-
A global model is trained on the server by receiving the local models from remotely deployed clients using Transmission Control Protocol (TCP). FL allows training a global model while safeguarding local data privacy and transferring knowledge across different buildings.
-
To choose the most suitable models for aggregation on the federated server, a method based on the normal distribution is introduced for client selection.
-
The proposed FL-based approach focuses on learning transferable knowledge from source buildings without compromising data privacy, utilizing this knowledge for predicting energy consumption in target buildings.
The rest of the paper is organized as follows: Section 2 discusses the related work of the proposed study and provides a critical analysis of existing studies. Section 3 presents the proposed methodology, which includes data collection and preparation, federated transfer learning (FTL) mechanisms, and a normal distribution-based client selection method. Section 4 presents the results of the proposed study, comparing them with existing state-of-the-art methods. Finally, Section 5 concludes the proposed study and suggests some future directions.
2 Related work
Federated Learning provides a collaborative learning framework to train a ML model exploiting locally available data and computing resources. This framework supports collaborative learning of ML models providing distributed optimization to handle large datasets [10]. FL is an emerging learning paradigm with significant possibilities in many industrial and engineering domains, including but not limited to image processing [11], medicine and healthcare [12, 13] autonomous vehicles [14], sentiment analysis [15], and name a few [16]. For speech-based model training, Leroy et al. [17] suggested a method based on FL. The proposed system employed an adaptive averaging technique that required fewer communication rounds. FedVision was introduced by Liu et al. [18] as a collaborative object-detection framework based Convolutional Neural Network (CNN). Chen et al. [19] proposed FedHealth to allow for the privacy-preserving training of individual ML models using health data. For their study, Briggs et al. [20] developed and integrated an FL scheme with Hierarchical Clustering (FLHC). In [21] MOCHA, a federated paradigm is proposed. The proposed work incorporated multi-task learning with FL [24, 25] while considering heterogeneous data distribution on each client.
A considerable drop in FL accuracy occurs when data is not independent and identically distributed (IID). For this reason, Zhao et al. [22] proposed that all nodes share a small data subset. This method, however, increased privacy and security concerns. Mohri et al. [23] present a new optimization method called agnostic FL, which updates the global model by averaging the gradients from individual clients.
It is important to note that none of the reviewed FL works [17–24] have been applied to the field of collaborative energy consumption prediction; hence their potential for electric consumption forecasting specifically is yet to be explored. Furthermore, while FL can collaboratively train a single global model, it may suffer from accuracy degradation if it is applied to data with widely varying distributions and energy consumption patterns, as measured by individual smart meters. In this research, we propose a fair client selection-based FL scheme for energy consumption forecasting in smart buildings and assess the advantages of FedAVG over a centralized method and standalone ML models for comparison.
Previous solutions formulated for energy consumption forecasting applied both simple as well as complex models. A detailed survey of recent developments in energy consumption forecasting is presented in [25]. It is evident from the findings of existing studies that Support Vector Machine (SVM), Artificial Neural Networks (ANN) [26], Deep Learning [27], Autoregressive (AR) [28], Moving Average (MA) and some regression models among others are extensively applied to the domain of energy forecasting [29, 30]. Simpler models such as AR and MA [31] employ a mathematical function assuming time series as stationary and are generally well suited for short-term load forecasts however suffer from severe performance degradation in the case of long-term forecasts. These models only take account of recent past happenings, ignoring the pattern of data that happened long ago in the past. On the other hand, regression-based solutions possess simpler architecture and are easy to implement. The ability of ANN to deal with complex patterns in time-series electric consumption data has made them one of the most appropriate choices in the field of energy consumption forecasting [32].
Recently DL frameworks have been widely employed for energy consumption prediction [10]. Long Short-Term Memory Networks (LSTM) hold a unique architecture that can handle long-term dependencies in data using gating structures [11]. Contemporary surveys on energy consumption forecasting supported the idea of using DL frameworks to improve the model’s predictive performance [12]. Article [13] presented a comparative analysis of seven commercial building energy load forecasting techniques. The experiment result of the study suggests that ANN outperformed SVM by achieving higher accuracy. However, due to many trainable parameters, ANN often suffers from getting stuck into local minima, which are unable to handle the complex load patterns that exist in residential contexts. Therefore, exploiting additional information such as energy end-use behavior and occupant intrinsic activities and routines helps improve model accuracy. Deep learning models are widely applied for energy consumption prediction due to their performance and ability to handle temporal correlation in complex time-series data. Some recent developments include the application of the Conditional Restricted Boltzmann Machine (CRBM) to forecast energy consumption [36]. In [2], the authors proposed an ensemble prediction model based on the Gated Recurrent Unit (GRU) and LSTM-RNN framework for short-term energy consumption forecasting.
The major limitation of conventional and AI-based solutions applied to energy consumption forecasting lies in centralized data placement that gives rise to issues such as security, privacy, unacceptable latency, and overloaded networks [37].
Despite the success of the investigated works [5, 38–40] for electric consumption forecasting, it is computationally expensive to train a single ML model for a single or group of smart meters due to a large number of the model’s trainable parameters. Furthermore, these methods require sharing data to a cloud or server for centralized training, which raises both network traffic and latency. These solutions introduce security and privacy issues since energy consumption data is uploaded to a centralized server. For instance, critical applications such as energy demand-response programs involve sensitive energy consumption data that translates into the smart home occupants’ end-use behaviors and intrinsic routines. Revealing such information can cause serious damage to the privacy of consumers. Clearly, the vulnerabilities of centralized training architectures have not been fully understood and mitigated yet. Taïk et al. [6] applied federated averaging for short-term load forecasting as a means to overcome these concerns. While Li et al. [41] applied weighted averaging to benefit from the FL. To anticipate power grid demand at EV charging stations, Saputra et al. [42] suggested combining FL with clustering. Initial attempts to introduce FL to the domain of energy consumption forecasting reviewed research [6, 41–43]. However, more research into FL’s strengths and weaknesses is required.
Instead, we propose a fair FL scheme using a performance-based weight aggregation mechanism involving clients with diverse data distribution. Regarding client participation, the server primarily performs two types of aggregation;
Full device participation: This method aggregates the weights of all registered clients without evaluating their performance. However, this approach can significantly degrade the global model’s performance. For instance, in a FL network with ten clients, if two clients exhibit poor performance, their inclusion in the collaborative training process negatively impacts the global model.
Partial device participation: In contrast, this method selects clients based on a variety of performance indicators. By aggregating weights only from high-performing clients, this approach aims to improve the overall quality of the global model. This selective aggregation is more pragmatic compared to full participation, as it mitigates the detrimental effects of underperforming clients. The proposed work employs a client selection technique based on a normal distribution. More specifically, we analyze the FL system behavior based on two client selection schemes: full participation and partial participation, and perform a comparison between the two FL approaches using FedAVG.
3 Methodology
3.1 Data preparation
The proposed work involved gathering data from eight residential buildings, which served as the source, and three other buildings as the target. Once the model was aggregated on the server, the knowledge obtained from the eight source buildings was transferred to the target buildings. When we collect data from sensors, there are chances of outliers due to sensor faults. To ensure the quality and reliability of the data, we utilized the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm to identify and remove outliers, thus cleaning the data. In each building, a Raspberry Pi device was deployed as a client to store and process the local data, which mainly included energy consumption and environmental parameters. Before using the data in our study, we preprocessed it by removing anomalies with the help of DBSCAN. This algorithm is particularly well-suited for our scenario as it takes into consideration the dense and sparse areas of the space, allowing us to effectively detect anomalies in the data. Moreover, temperature and humidity sensors were deployed on the constrained devices to provide real-time measurements of environmental parameters. Since all the residential buildings were located in the same area, sensors were only deployed on the server to obtain the environmental parameters for the entire region.
Furthermore, the electricity consumption for each apartment has an hourly temporal granularity, and additional temporal aspects, such as the time of day, month of the year, and year, are derived from preexisting features. The list of the features used in the experiments is shown in Table 1.
Extracted and existing features of energy dataset.
In federated transfer learning, multiple clients contribute their data to a central server where a global model is trained on the combined data. The global model is then sent back to the clients where it is fine-tuned on their local data to improve the model’s performance. The distribution of the data on each client is important in federated transfer learning, as it affects the quality of the global model and the fine-tuning process. Information about the distribution of data among various clients can be found in Table 2. According to the Table 2, the first 8 clients are considered source clients and are information-rich because they have more samples as compared to the target client. The source clients are used to train the global model in the initial stage, which is then fine-tuned on the data from the target client to improve its performance on the target building. The target building’s data is used to fine-tune the global model because it represents the real-world scenario and helps the model adapt to the specific characteristics of the target building. The fine-tuning process ensures that the global model is optimized for the target building, which results in accurate energy consumption prediction.
Data distribution details for each FL source and target client.
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of mean absolute error.
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of mean squared error.
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of R2 score.
Results of proposed model on target clients in terms of MAE, MSE, and R2 score.
The server is designed to send the initial configuration to the clients, as shown in Figure 1. The user sets the initial configuration by informing the server of the IP addresses and ports of the registered clients. Additionally, the user sets the configuration for FL, including the number of server rounds, local epochs, data to be used, and the model to be used in the FL process. The server receives the configuration file from the user and generates separate configuration files for all registered clients, as depicted in Figure 1. The server is connected to the clients via the TCP protocol to send and receive model weights. Each client is assigned a unique ID to differentiate the received model and send back the aggregated models. The architecture of the initial model is also designed on the server because the used data is IID (independent and identically distributed). To configure the training parameters, a JSON file is dispatched to each client, which is then utilized by the clients.
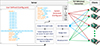 |
Fig. 1 Configuration of the clients and communication protocol between server and clients. |
Each FL client represents a building with its private data. All clients use their local privacy-sensitive data to train the model and share their local updates with the server based on the horizontal FL setting. In horizontal FL, data is distributed across different devices or clients, each holding a subset of the data. This distribution is termed horizontal because each client has a different set of data samples rather than a different set of features, as seen in vertical FL.
The process begins with the registration of FL clients to the server using their IP addresses and ports. Each client device has a unique IP address that enables communication with the server in the FL setup.
Figure 2 shows the pipeline of the proposed model where firstly (1) the energy consumption data collection from the smart meter. Each smart home collects data on energy consumption from its own smart meter. Secondly (2) the data collected by smart homes is stored in the building-level datalog. After that, clients share metadata with the server in order to train a model using local data. In turn, (3) the server shares the initial global model architecture with the clients. Model architecture refers to the model’s structure and design, including the number of layers, type of layers, and number of units in each layer. Sharing the model architecture with the clients can assist in protecting the confidentiality of the data used to train the models since the data does not need to be sent to the server. After receiving the initial global model, (4) the clients start the local training using the privacy-sensitive data. When model training is complete, (5) the resulting local model weights are uploaded to the server in a compacted JSON format. The server will wait until all client local updates are received. After the server has received models from all currently registered clients, (6) it will filter out weak models and begin the model aggregation process (7). The performance of the weak model needs to be improved in terms of accuracy and other evaluation criteria. In an FL arrangement, the performance of the final model can be impacted by the performance of the local models. The goal of the proposed system is to filter out local models with lower performance such that their contribution is minimal in the global aggregation process. After aggregation using federated averaging, each client will receive an update of the global model. After receiving global updates, all clients fine-tune the model, and this process continues until the convergence of the global model.
 |
Fig. 2 Proposed FL model for energy consumption prediction. |
Federated transfer learning is a concept where knowledge from one group of clients is transferred to another group of clients. A federated server aggregates the received model and sends it back to the registered clients, who then train the received model for a specified number of epochs and send it back to the server. This process continues for a set number of server rounds. In FTL, after each aggregation, the server sends the model to both registered source and target clients. The target clients validate the performance of the received model on their local data. Figure 3 illustrates the knowledge transfer process from the source building to the target building. Each source building denoted as S1, S2, …, Sn possesses its own localized data that is utilized to train the local model partially. Subsequently, these locally trained models’ weights are transmitted to a central server. The server employs a client selection strategy (explained in Sect. 3.2), followed by model aggregation exclusively on the chosen models. The resultant aggregated model is then broadcasted to both source and target clients (T1, T2, …, Tn). The source clients accept the received model and initiate a retraining process for a defined number of epochs, subsequently transmitting the retrained model weights back to the server. In contrast, the target clients exclusively perform validation on the received models using dedicated validation data, culminating in the selection of the most superior model from the collection of previously received iterations.
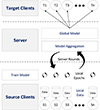 |
Fig. 3 Federated Transfer Learning: Transferring the information from source client to target client. |
3.2 Client participation
Client participation based on performance evaluation guarantees high-quality model updates from all participating devices, thereby significantly boosting the quality of the trained model in FL. In the proposed work, the metric selected for client selection is a normal distribution-based performance evaluation. The term “normal distribution” is used in the context of measuring performance because it represents a probability distribution where a given variable tends to fall around the middle of a bell-shaped curve. The normal distribution is selected to select the best model based on its placement on the bell curve of the normal distribution. To select the top-performing models for global model aggregation, the normal distribution is utilized. It creates a bell curve that depicts the mean and standard deviation of the given set of values. This curve is divided into four quarters, and based on their performance, the best clients are chosen for participation in the global model aggregation process. The normal distribution is employed to select the optimal model based on its placement along the bell curve. Models located within a valid quartile of the bell curve will be chosen for aggregation.
The local models are aggregated using the following weight update formulation: 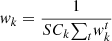 where SC represents the selected clients for kth round of the server based on the normal distribution-based client’s selection scheme given as:
where SC represents the selected clients for kth round of the server based on the normal distribution-based client’s selection scheme given as: 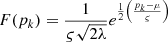 . Here pk represents the client’s performance and
. Here pk represents the client’s performance and 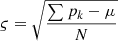 is quantified as the standard deviation of all client’s performance. Algorithm 1 shows the client’s local training and sending of the partially trained model to the server. The procedure gets the local data as input and trains the local model. Firstly, the configuration parameters for the FL framework are initialized. This includes the activation of both sender and receiver components, specification of the number of epochs and rounds, and the establishment of the local model’s architecture. Secondly, the local training procedure unfolds over a series of r rounds. Within each round, the local model is trained for a designated number of local epochs, denoted as e. The loss function, represented as l(.;.), is computed, and the resultant local model, along with its corresponding loss, is conveyed to the central server using the TCP sender mechanism. Each client’s model contributes to the server’s aggregation process with its respective weight. Upon reception of the updated aggregated weights denoted as wa through the TCP receiver, these weights are incorporated into the model. This triggers the retraining process, enhancing the model’s performance based on the aggregated knowledge.
is quantified as the standard deviation of all client’s performance. Algorithm 1 shows the client’s local training and sending of the partially trained model to the server. The procedure gets the local data as input and trains the local model. Firstly, the configuration parameters for the FL framework are initialized. This includes the activation of both sender and receiver components, specification of the number of epochs and rounds, and the establishment of the local model’s architecture. Secondly, the local training procedure unfolds over a series of r rounds. Within each round, the local model is trained for a designated number of local epochs, denoted as e. The loss function, represented as l(.;.), is computed, and the resultant local model, along with its corresponding loss, is conveyed to the central server using the TCP sender mechanism. Each client’s model contributes to the server’s aggregation process with its respective weight. Upon reception of the updated aggregated weights denoted as wa through the TCP receiver, these weights are incorporated into the model. This triggers the retraining process, enhancing the model’s performance based on the aggregated knowledge.
Data: Local Dataset (x1, y1), (x2, y2), … (xn, yn)
Result: (Local Model)
Initialization;
Register Client on Server (config.json)
rsvr ← (Activate Receiver)
// Initial Configuration
conf ← rsvr.receiveConfig();
sndr
← PrepareSender(conf.serverIP, conf.serverPort)
dataset ← conf.dataset
e ← conf.local_epochs
// Get model for server
model ← getModel(conf.model);
t,r ← 0
while r<conf.server_rounds do
t ← r × e
// Train local model of specified epochs
model.train(dataset,e)
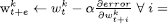
1, 2, …, e // where k is client number
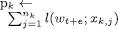 //n is number of samples for k client and l(.;.) is loss function
//n is number of samples for k client and l(.;.) is loss function
sndr.send 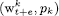
// Wait for server to complete aggregation
…
wa ← rsvr.receive_weights
model.setWeights(wa)
round++;
end
Algorithm 2 shows how the client’s model is received at the server and how the partial clients participate in global model aggregation. Similar to the client-side procedure, the server activates its receiver and sender functionalities to accept local models from clients and broadcast the global model respectively. The server begins by acquiring the profiles of all registered clients, denoted as clientsconfig, to facilitate the dissemination of global models. It then enters a waiting state, monitoring the training progress of all clients as they train their respective local models and transmit them to the server. This synchronization occurs for a predefined number of rounds, r. Upon reception of the locally trained models through the TCP receiver, the server uses the performance metrics of these models to identify the best-performing candidates using the normal distribution method. The selected models, represented as St, are subsequently aggregated to produce a global model, and the resulting aggregated weights denoted as wa are distributed to the registered clients via the TCP sender mechanism.
Data: Local Partially Trained Models
(m1 ,m2, …, mn)
Results: Aggregated weights waf
Initialization;
rsvr ← (Activate Receiver)
sndr ← (Prepare Sender)
// User defined Configuration config.json
clients_confign [] ←
prepare_clients_config (config.json) Figure 1
sndr.broadcast(clients_confign)
// Initial Server Configuration
server_conf
← getServerConfiguration(config.json);
rounds ← 0
while rounds<conf.serverRounds do
// Wait for clients to complete partial training
…
while ! allModelsReceived do
all_models ← rsvr.getModel()
end
wk ← all_models.paramaeters ∀ k = (1,2,…,N)
pk ← all_models.p ∀ k = (1,2,…,N)
// Where pk is performance of client k
sndr.broadcast(wa)
round++;
end
One of the most important characteristics of the normal distribution is that it is symmetrical around its mean, which means that values on either side of the mean have an equal probability of occurring. It has been found that the normal distribution is helpful in performance evaluation when trying to understand how performance scores are distributed. In the case of a normally distributed set of performance scores, one might, for instance, calculate the fraction of clients who achieved a specific score or compare the performance of different participating clients. For each server round, the loss distribution is calculated, and clients are chosen based on a certain quartile-based threshold. The quartiles of a normal distribution are numbers that divide the performance scores of clients into four equal portions, each containing 25% of the data. The first quartile, often known as the lower quartile or Q1, is the value that divides the bottom 25% of the performance scores from the top 75%. The second quartile, often known as the median, is a value that divides the lowest and highest 50% of the performance scores. The third quartile, usually referred to as the upper quartile or Q3, is a value that divides the bottom 75% of the performance scores from the top 25%. Quartiles can efficiently evaluate the performance of clients in FL. For instance, if we want to evaluate the performance of two clients If a client’s first quartile is much lower than the second client’s first quartile, it is indicative of poor performance on the part of the first client and vice-versa.
4 Results
4.1 Evaluation metrics
The following metrics are used to evaluate the model performance.
Mean absolute error
Mean absolute error (MAE) is the absolute difference between actual yi and observed values 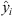 as shown in equation.
as shown in equation.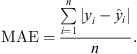 (1)
(1)
Mean square error
Mean square error (MSE) is the square of the difference between actual yi and predicted 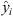 values as shown in the equation below
values as shown in the equation below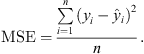 (2)
(2)
R2 score
The R2 score measures the accuracy of the model in fitting the data. The higher value of R2 indicates the accuracy of the model. The best possible value of R2 is 1 and it can also be negative. The equation below shows the R2 score from Sum of Squares Residual (SSR) 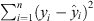 and Sum of Squares Total (SST)
and Sum of Squares Total (SST) 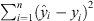 , where y − i is the actual value and
, where y − i is the actual value and 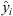 is the predicted value.
is the predicted value.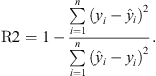 (3)
(3)
4.2 Performance evaluation of proposed model
The proposed model is being compared with existing ML regression models and ensemble regression models for source buildings, while the federated full participation and partial participation are being compared for target buildings. The results are compared in terms of MAE, MSE, and R2 to show the effectiveness of the proposed model. Table 3 shows the results of proposed and state-of-the-art ML models in terms of mean absolute error for source buildings. The results show that the proposed model outperforms as compared to other models. The existing model is implemented from the sklearn library of Python, while the proposed model is implemented from scratch. The source code is available on GitHub (https://github.com/atifrizwan1/TFL-PP). The average column displays the model’s average performance across all clients. The globally trained model is utilized by the clients after training. In simpler terms, the average performance reflects the final global model’s performance. The performance indicates that the proposed FedLSTM, with partial participation, outperforms its counterparts. The DNN model, with both partial and full participation, shows better performance compared to state-of-the-art ML models. The local models are trained for 5 epochs and 100 server rounds. The default parameters of LSTM and DNN models are used. No individual early stopping criteria are applied to the models. Instead, we use server-based early stopping criteria for the global model. Training is halted when the global model converges.
By using the client selection model, we compared the results with those of DL models for source buildings that employed full participation and independent training. While full participation sometimes deteriorated the global model in certain server rounds, the exclusion of models from the aggregation process improved the accuracy of the global model. From the start of the art ML models, Linear Regression (LR) is the model simplest regression model that maps a linear line on the data and predicts future values. The Light Gradient-Boosting Machine (LGBM) model is based on decision tree regression and gradient boosting techniques. This model uses the AutoML pipeline to train various DT models and predict the value of the target attribute. The results of the LGBM regressor are better than some other models for some clients. As, the decision tree model, is based on the rules, so the rules can be more accurate for less data. So, when the data is divided into clients, the LGBM model performs well as compared to others.
Extreme Gradient Boosting (XGBoost) is a widely used and efficient implementation of the gradient boosting algorithm for decision tree ensembles. It can be applied to regression (XGBRegressor) and classification (XGBClassifier) tasks. Gradient boosting is a ML technique that combines multiple weak models, such as decision trees, to form a stronger model. The process involves training a new model to predict the residual error of the previous model and then adding the predictions of the new model to the predictions of the previous model, thereby incrementally improving the overall model performance.
The machine learning approach of gradient boosting merges several relatively weak models (such as decision trees) into a single, more robust model. The process involves training a second model to forecast the first model’s residual error and then combining the two sets of predictions. This procedure is repeated until an appropriate model is created. The optimal weights are used to develop a model that is a weighted sum of all the individual models. Further CatBoost (Category Boosting) is a regressor that performs gradient boosting on ensembles of decision trees. CatBoost is developed by Yandex and is ideal for processing categorical information. CatBoost, similar to XGBoost, has regression and classification components (CatBoostRegressor and CatBoostClassifier, respectively). The automatic handling of missing values and categorical variables by CatBoost is a notable advantage that can substantially reduce the need for preprocessing, resulting in time savings. Moreover, the model incorporates various hyper-parameters, including the learning rate, tree depth, and number of trees in the ensemble, which may be fine-tuned to improve the performance of the model. Another optimization method known as Stochastic Gradient Descent (SGD) is both easy to implement and highly accurate when applied to linear regression. The functioning of the SGD involves the iterative adjustment of the model weights in a manner that minimizes the loss function. This adjustment is carried out by utilizing the gradient of the loss function with respect to the weights.
The utilization of ensemble regressors is implemented to predict energy consumption in intelligent buildings. These prediction results are then compared with the results obtained from a DL model that has been developed for a federated environment. The mean squared error comparison of ensemble models, DL models, and proposed FL models is presented in Table 4. The presented results also include the average performance of all models, which indicates that the proposed model with partial client engagement exhibits enhanced performance in comparison to both full participation and state-of-the-art ML models.
Table 5 shows the performance of the proposed model and state-of-the-art ML models in terms of R2 score. The higher value of R2 shows the better performance of the model. The results show that the proposed model outperforms as compared to existing models. The partial participation of SL nodes in the aggregation process shows better performance as compared to full participation for source buildings. The results are computed after each server round and the average results are reported. The average performance of the final global model is also shown in Table 5. With an R2 score of 88.68 for LSTM and 87.85 for DNN, the global model’s performance with partial participation is the highest.
The global loss is defined as the loss of all the clients on each server round. The average loss of all clients on the server is considered as a global loss. The global loss of the DNN and LSTM models is shown in Figures 4 and 5. After completing a set number of local epochs, aggregation is conducted on the server to obtain the global model. Figures 4 and 5 clearly illustrate that upon receiving the model from clients, the error of the local model increases. This occurs due to the aggregation of knowledge from all or a subset of selected clients, resulting in changes to the weights of the resultant global model. Hence, it is necessary to perform more fine-tuning on the weights. Following multiple iterations of this procedure, the global model reaches convergence. Figures 4 and 5 show the convergence of the global model on the server, with respect to source buildings. After achieving satisfactory convergence, the global model is subsequently transmitted to the target buildings for additional training.
 |
Fig. 4 Convergence of global DNN model on 50 server rounds. a) Mean absolute error; b) Mean square error. |
 |
Fig. 5 Convergence of global LSTM model on 50 server rounds. a) Mean absolute error; b) Mean square error. |
In the realm of FL, the computation of the global loss involves consolidating the individual losses incurred by all the clients on the server. The global loss reflects the model’s performance on the entire dataset and is used to track convergence as training progresses. Once the global model achieves convergence for the source buildings, it is exported to facilitate the training process for the target buildings.
Federated transfer learning leverages data from one group of devices to enhance the training process of another group. This enhancement improves training efficiency and reduces data requirements on the target devices by transferring the converged model to them. Subsequently, the aggregated global model is distributed to the clients, enabling them to build an optimal model for the desired structures. After each server iteration, the designated clients validate the global model against their datasets. Upon completing the training process, each target client adopts the best model based on the received training history.
The results of the global model on the validation data of the target clients are presented in Table 6. The performance of the model utilized by the target clients reveals that LSTM with partial participation shows superior outcomes compared to other models, demonstrating better results with an average of 88.92 for DNN and 88.15 for LSTM.
The results of the proposed study show that the partial participation of clients for aggregation in the global model performs better as compared to full client participation. Moreover, the knowledge transferred to a target building from best-selected clients is better as compared to full participation.
5 Conclusion
To forecast energy consumption, many forecasting models have been extensively studied in the literature for residential, commercial, and industrial buildings. However, training personalized models for densely populated and heavily dynamic urban areas is challenging. Furthermore, concerns about the privacy of fine-grained energy consumption data in residential buildings make it difficult to gather the necessary data. To address these challenges, we propose a privacy-preserving collaborative FL framework that enables learning a uniform model across many residential buildings. Our approach leverages state-of-the-art DL methods incorporating environmental factors and spatial and temporal energy consumption to forecast energy consumption accurately. We thoroughly investigate the impact of temporal and spatial granularity on the predictive power of the privacy-preserved FL framework. We proposed a normal distribution-based client selection method to choose the best clients for aggregation. By dividing the region into four quartiles and selecting the clients in the first three quartiles, we ensure that bad models do not negatively impact the global model or affect the performance of all clients. We compare the performance of our method with those of full and partial participation DL models for both DNN and LSTM models. Federated Transfer Learning in our approach facilitates the transfer of knowledge from information-rich buildings to information-poor buildings. Our results demonstrate that partial participation in the global model is effective in optimizing performance for each client, including the target clients. Specifically, FedLSTM with partial participation achieved an average R2 score of 88.68 for source buildings and 88.15 for target buildings. Additionally, we visualize the convergence of the global model across all server rounds. This study contributes to the field of energy consumption forecasting by introducing a novel approach that addresses data heterogeneity and privacy concerns in FL settings.
In future work, this study can be extended by implementing a partial model transfer approach, where a portion of the model is transferred and the remaining part is trained on the target client. This method allows for personalization while retaining generalization capabilities from the source model. Additionally, the scope of the experiments can be broadened to encompass a larger dataset of buildings, further validating the robustness and scalability of the proposed framework.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0454.
Funding
Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funded this research work through project number RI-44-0454.
Conflicts of interest
The authors declare no competing interests.
Data availability statement
The results reported in this study are reproducible and the source code is available on GitHub (https://github.com/atifrizwan1/TFL-PP).
Author contribution statement
Conceptualization, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H., R.A.; methodology, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H., R.A.; validation, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H., R.A.; formal analysis, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H., R.A.; investigation, A.R., A.N.K., R.A., G.A., H.Z.H., R.A.; resources, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H.; data curation, A.R., A.N.K., R.A.,; writing – original draft preparation, A.R., A.N.K., R.A., G.A., N.A.S., H.Z.H., R.A.; writing – review and editing, A.R., A.N.K., R.A., G.A., H.Z.H., R.A.; visualization, A.R., A.N.K., G.A., N.A.S., H.Z.H., R.A.; supervision, R.A., G.A and H.Z.H.; project administration, R.A., G.A.; funding acquisition, R.A. and G.A. All authors have read and agreed to the published version of the manuscript.
References
- Khan A.N., Iqbal N., Ahmad R., Kim D.H. (2021) Ensemble prediction approach based on learning to statistical model for efficient building energy consumption management, Symmetry 13, 3, 405. https://doi.org/10.3390/sym13030405. [CrossRef] [Google Scholar]
- Khan A.N., Iqbal N., Rizwan A., Ahmad R., Kim D.H. (2021) An ensemble energy consumption forecasting model based on spatial-temporal clustering analysis in residential buildings, Energies 14, 11, 3020. https://doi.org/10.3390/en14113020. [CrossRef] [Google Scholar]
- Notton G., Voyant C. (2018) Chapter 3 – Forecasting of intermittent solar energy resource, in: Yahyaoui I. (ed), Advances in renewable energies and power technologies, Elsevier, pp. 77–114. https://doi.org/10.1016/B978-0-12-812959-3.00003-4. [CrossRef] [Google Scholar]
- Hurst W., Montañez C.A.C., Shone N. (2020) Time-pattern profiling from smart meter data to detect outliers in energy consumption, IoT 1, 92–108. https://doi.org/10.3390/iot1010006. [CrossRef] [Google Scholar]
- Arif A., Javaid N., Anwar M., Naeem A., Gul H., Fareed S. (2020) Electricity load and price forecasting using machine learning algorithms in smart grid: a survey, in: Barolli L., Amato F., Moscato F., Enokido T., Takizawa M. (eds), Web, artificial intelligence and network applications, Springer International Publishing, Cham, pp. 471–483. https://doi.org/10.1007/978-3-030-44038-1_43. [CrossRef] [Google Scholar]
- Taïk A., Cherkaoui S. (2020) Electrical load forecasting using edge computing and federated learning, in: ICC 2020 – 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June, IEEE, pp. 1–6. https://doi.org/10.1109/ICC40277.2020.9148937. [Google Scholar]
- Truong N., Sun K., Wang S., Guitton F., Guo Y. (2021) Privacy preservation in federated learning: An insightful survey from the GDPR perspective, Comput. Secur. 110, 102402. https://doi.org/10.1016/j.cose.2021.102402. [CrossRef] [Google Scholar]
- Bonawitz K., Eichner H., Grieskamp W., Huba D., Ingerman A., Ivanov V., Kiddon C., Konečný J., Mazzocchi S., McMahan B. (2019) Towards federated learning at scale: System design, Proc. Mach. Learn. Syst. 1, 374–388. https://doi.org/10.48550/arXiv.1902.01046. [Google Scholar]
- Yang Q., Liu Y., Chen T., Tong Y. (2019) Federated machine learning: Concept and applications, ACM Trans. Intell. Syst. Technol. 10, 2, 1–19. https://doi.org/10.48550/arXiv.1902.04885. [Google Scholar]
- Ahmed K.M., Imteaj A., Amini M.H. (2021) Federated deep learning for heterogeneous edge computing, in: 2021 20th IEEE International Conference on Machine Learning and Applications (ICMLA), Pasadena, CA, USA, 13–16 December, IEEE, pp. 1146–1152. https://doi.org/10.1109/ICMLA52953.2021.00187. [Google Scholar]
- Liu W., Chen L., Chen Y., Zhang W. (2020) Accelerating federated learning via momentum gradient descent, IEEE Trans. Parallel Distrib. Syst. 31, 8, 1754–1766. https://doi.org/10.48550/arXiv.1910.03197. [CrossRef] [Google Scholar]
- Wu X., Liang Z., Wang J. (2020) Fedmed: a federated learning framework for language modeling, Sensors 20, 14, 4048. https://doi.org/10.3390/s20144048. [CrossRef] [PubMed] [Google Scholar]
- Brisimi T.S., Chen R., Mela T., Olshevsky A., Paschalidis I.C., Shi W. (2018) Federated learning of predictive models from federated electronic health records, Int. J. Med. Inform. 112, 59–67. https://doi.org/10.1016/j.ijmedinf.2018.01.007. [CrossRef] [Google Scholar]
- Pokhrel S.R., Choi J. (2020) Federated learning with blockchain for autonomous vehicles: analysis and design challenges, IEEE Trans. Commun. 68, 8, 4734–4746. https://doi.org/10.1109/TCOMM.2020.2990686. [CrossRef] [Google Scholar]
- Wang Y., Tong Y., Shi D. (2020) Federated latent dirichlet allocation: a local differential privacy based framework, Proc. AAAI Conf. Artif. Intell. 34, 4, 6283–6290. https://doi.org/10.1609/aaai.v34i04.6096. [Google Scholar]
- Li L., Fan Y., Tse M., Lin K.Y. (2020) A review of applications in federated learning, Comput. Ind. Eng. 149, 106854. https://doi.org/10.1016/j.cie.2020.106854. [CrossRef] [Google Scholar]
- Leroy D., Coucke A., Lavril T., Gisselbrecht T., Dureau J. (2019) Federated learning for keyword spotting, in: ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May, IEEE, pp. 6341–6345. [Google Scholar]
- Liu Y., Huang A., Luo Y., Huang H., Liu Y., Chen Y., Feng L., Chen T., Yu H., Yang Q. (2020) Fedvision: an online visual object detection platform powered by federated learning, Proc. AAAI Conf. Artif. Intell. 34, 8, 13172–13179. https://doi.org/10.48550/arXiv.2001.06202. [Google Scholar]
- Chen Y., Qin X., Wang J., Yu C., Gao W. (2020) Fedhealth: a federated transfer learning framework for wearable healthcare, IEEE Intell. Syst. 35, 4, 83–93. https://doi.org/10.48550/arXiv.1907.09173. [CrossRef] [Google Scholar]
- Briggs C., Fan Z., Andras P. (2020) Federated learning with hierarchical clustering of local updates to improve training on non-IID data, in: 2020 International Joint Conference on Neural Networks, IJCNN 2020, Glasgow, United Kingdom, 19–24 July, IEEE, pp. 1–9. https://doi.org/10.48550/arXiv.2004.11791. [Google Scholar]
- Smith V., Chiang C.-K., Sanjabi M., Talwalkar A.S. (2017) Federated multi-task learning, in: Guyon I., Von Luxburg U., Bengio S., Wallach H., Fergus R., Vishwanathan S., R. Garnett (eds), Advances in neural information processing systems, vol. 30, Curran Associates, Inc. Available at https://proceedings.neurips.cc/paper_files/paper/2017/file/6211080fa89981f66b1a0c9d55c61d0f-Paper.pdf. [Google Scholar]
- Zhao Y., Li M., Lai L., Suda N., Civin D., Chandra V. (2018) Federated learning with non-IID data. Preprint. https://doi.org/10.48550/arXiv.1806.00582. [CrossRef] [Google Scholar]
- Mohri M., Sivek G., Suresh A.T. (2019) Agnostic federated learning, in: Chaudhuri K., Salakhutdinov R. (eds), Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June, PMLR, pp. 4615–4625. https://doi.org/10.48550/arXiv.1902.00146. [Google Scholar]
- Konečný J., McMahan B., Ramage D. (2015) Federated optimization: distributed optimization beyond the datacenter, Preprint. https://doi.org/10.48550/arXiv.1511.03575. [Google Scholar]
- Yildiz B., Bilbao J.I., Dore J., Sproul A.B. (2017) Recent advances in the analysis of residential electricity consumption and applications of smart meter data, Appl. Energy 208, 402–427. https://doi.org/10.1016/j.apenergy.2017.10.014. [CrossRef] [Google Scholar]
- Kaytez F., Taplamacioglu M.C., Cam E., Hardalac F. (2015) Forecasting electricity consumption: a comparison of regression analysis, neural networks and least squares support vector machines, Int. J. Electr. Power Energy Syst. 67, 431–438. https://doi.org/10.1016/j.ijepes.2014.12.036. [CrossRef] [Google Scholar]
- Amasyali K., El-Gohary N.M. (2018) A review of data-driven building energy consumption prediction studies, Renew. Sustain. Energy Rev. 81, 1192–1205. https://doi.org/10.1016/j.rser.2017.04.095. [CrossRef] [Google Scholar]
- Gajowniczek K., Ząbkowski T. (2017) Electricity forecasting on the individual household level enhanced based on activity patterns, PLoS One 12, 4, e0174098. https://doi.org/10.1371/journal.pone.0174098. [CrossRef] [PubMed] [Google Scholar]
- Raza M.Q., Khosravi A. (2015) A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings, Renew. Sustain. Energy Rev. 50, 1352–1372. https://doi.org/10.1016/j.rser.2015.04.065. [CrossRef] [Google Scholar]
- Rizwan A., Khan A.N., Ahmad R., Kim D.H. (2022) Optimal environment control mechanism based on ocf connectivity for efficient energy consumption in greenhouse, IEEE Internet Things J. 10, 6. https://doi.org/10.1109/JIOT.2022.3222086. [Google Scholar]
- Mahia F., Dey A.R., Masud M.A., Mahmud M.S. (2019) Forecasting electricity consumption using ARIMA model, in: 2019 International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 24–25 December, IEEE, pp. 1–6. https://doi.org/10.1109/STI47673.2019.9068076. [Google Scholar]
- Li K., Hu C., Liu G., Xue W. (2015) Building’s electricity consumption prediction using optimized artificial neural networks and principal component analysis, Energy Build. 108, 106–113. https://doi.org/10.1016/j.enbuild.2015.09.002. [CrossRef] [Google Scholar]
- Briggs C., Fan Z., Andras P. (2021) Federated learning for short-term residential energy demand forecasting, Preprint. https://doi.org/10.48550/arXiv.2105.13325. [Google Scholar]
- Wei N., Li C., Peng X., Zeng F., Lu X. (2019) Conventional models and artificial intelligence-based models for energy consumption forecasting: a review, J. Pet. Sci. Eng. 181, 106187. https://doi.org/10.1016/j.petrol.2019.106187. [CrossRef] [Google Scholar]
- Edwards R.E., New J., Parker L.E. (2012) Predicting future hourly residential electrical consumption: a machine learning case study, Energy Build. 49, 591–603. https://doi.org/10.1016/j.enbuild.2012.03.010. [CrossRef] [Google Scholar]
- Mocanu E., Nguyen P.H., Gibescu M., Kling W.L. (2016) Deep learning for estimating building energy consumption, Sustain. Energy Grids Netw. 6, 91–99. https://doi.org/10.1016/j.segan.2016.02.005. [CrossRef] [Google Scholar]
- Tun Y.L., Thar K., Thwal C.M., Hong C.S. (2021) Federated learning based energy demand prediction with clustered aggregation, in: 2021 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju Island, Korea (South), 17–20 January, IEEE, pp. 164–167. https://doi.org/10.1109/BigComp51126.2021.0003.9 [Google Scholar]
- Fekri M.N., Patel H., Grolinger K., Sharma V. (2021) Deep learning for load forecasting with smart meter data: online adaptive recurrent neural network, Appl. Energy 282, 116177. https://doi.org/10.1016/j.apenergy.2020.116177. [CrossRef] [Google Scholar]
- Sehovac L., Grolinger K. (2020) Deep learning for load forecasting: sequence to sequence recurrent neural networks with attention, IEEE Access 8, 36411–36426. https://doi.org/10.1109/ACCESS.2020.2975738. [CrossRef] [Google Scholar]
- Tian Y., Sehovac L., Grolinger K. (2019) Similarity-based chained transfer learning for energy forecasting with Big Data, IEEE Access 7, 139895–139908. https://doi.org/10.1109/ACCESS.2019.2943752. [CrossRef] [Google Scholar]
- Li J.B., Ren Y.Q., Fang S.W., Li K.C., Sun M.Y. (2020) Federated learning-based ultra-short term load forecasting in power internet of things, in: 2020 IEEE International Conference on Energy Internet (ICEI), Sydney, NSW, Australia, 24–28 August, IEEE, pp. 63–68. https://doi.org/10.1109/ICEI49372.2020.00020. [Google Scholar]
- Saputra Y.M., Hoang D.T., Nguyen D.N., Dutkiewicz E., Mueck M.D., Srikanteswara S. (2019) Energy demand prediction with federated learning for electric vehicle networks, in: 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December, IEEE, pp. 1–6. https://doi.org/10.48550/arXiv.1909.00907. [Google Scholar]
- Fekri M.N., Grolinger K., Mir S. (2022) Distributed load forecasting using smart meter data: federated learning with recurrent neural networks, Int. J. Electr. Power Energy Syst. 137, 107669. https://doi.org/10.1016/j.ijepes.2021.107669. [CrossRef] [Google Scholar]
All Tables
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of mean absolute error.
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of mean squared error.
Comparison of proposed FedDNN and FedLSTM models with existing models in terms of R2 score.
All Figures
 |
Fig. 1 Configuration of the clients and communication protocol between server and clients. |
| In the text | |
 |
Fig. 2 Proposed FL model for energy consumption prediction. |
| In the text | |
 |
Fig. 3 Federated Transfer Learning: Transferring the information from source client to target client. |
| In the text | |
 |
Fig. 4 Convergence of global DNN model on 50 server rounds. a) Mean absolute error; b) Mean square error. |
| In the text | |
 |
Fig. 5 Convergence of global LSTM model on 50 server rounds. a) Mean absolute error; b) Mean square error. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.