| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 70 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.2516/stet/2024069 | |
| Published online | 27 September 2024 | |
Regular Article
Research on optimization method of CCHP system coupled with renewable energy
1
School of Civil Engineering and Architecture, Hebei University of Science and Technology, 26 Yuxiang Street, Yuhua District, Shijiazhuang 050018, PR China
2
School of Energy, Power and Mechanical Engineering, North China Electric Power University, 2 Beinong Road, Huilongguan, Changping District, Beijing 102206, PR China
* Corresponding author: ligaikang@hebust.edu.cn
Received:
5
March
2024
Accepted:
16
August
2024
Renewable energy is widely used in combined cooling, heating and power (CCHP) systems. This is important for building a low-carbon, flexible, multi-energy complementary energy system. However, coupling different renewable energy sources can have a somewhat differentiated impact on the performance of the system. In this study, an approach combining a long short-term memory (LSTM) network with multiple optimization algorithms is proposed. Comparative performance analysis of CCHP systems coupling solar and wind subsystems is conducted. Firstly, the renewable energy output is predicted by LSTM. Then, the Pareto frontiers of the coupled renewable energy CCHP system are generated by the Non-dominated Genetic Sorting Algorithm. The results are fed into the distance between superior and inferior solution methods to arrive at a decision, completing the multi-objective optimization of the system. Results show that the CCHP system coupling photovoltaic (PV) and solar collector (ST) is superior to the CCHP system coupling photovoltaic-photovoltaic-thermal integrated device. The system performance can be further improved by adding wind turbines to the integrated system coupling PV and ST.
Key words: CCHP system / Renewable energy / LSTM / NSGA-II / TOPSIS
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The increasing global consumption of fossil energy has led to a series of environmental and ecological problems [1]. In the face of the impact of energy consumption and greenhouse gas emissions on human society, there is an urgent need to optimize the energy system and establish a more ecological and environmentally friendly energy system [2, 3]. The combined cooling, heating and power (CCHP) system enables the gradual utilization of energy and integrates multiple energy supply methods [4]. Traditional CCHP systems use natural gas as the primary energy source to power the system, which is not easy to maximize the advantages of energy saving and emission reduction [5, 6]. It is necessary to increase the penetration of renewable energy sources and to reduce carbon dioxide emissions [7].
In recent years, there has been a lot of research on the CCHP system of coupled solar energy, biomass energy, wind energy, geothermal energy and other renewable energy [8].
For example, in the research of CCHP systems with coupled solar energy are: Ma et al. [9] proposed an interval scheduling method for CCHP systems with coupled solar energy to optimize system performance. Jia et al. [10] proposed a novel CCHP system combining an organic Rankine cycle and a solar thermal (ST) to compare the CCHP system and the annual total cost-saving rate (ATCSR) under an electrical tracking strategy. Soheyli et al. [11] proposed a CCHP system including photovoltaic (PV), wind turbine (WT), and solid oxide fuel cell as prime movers using a multi-objective particle swarm optimization algorithm to determine the optimal number of each system component. Ren et al. [12] optimized and compared a hybrid CCHP system for three buildings under different operating strategies: In system A solar energy is converted to heat and electricity by ST and PV respectively, and solar energy in system B is converted to thermal and electrical energy by a photovoltaic thermal solar collector (PVT). Ge et al. [13] proposed a solar-assisted natural gas-distributed energy system with energy storage, designed three scenarios with different structures, and investigated their optimized configurations. Hassan et al. [14] modelled and analyzed devices that combined solar photovoltaic cells, wind turbines, micro-gas turbines and lithium-ion batteries to improve the utilization ratio of renewable energy. Huneke et al. [15] proposed a hybrid power system including PV, WT, diesel generator and batteries, which was optimized using linear programming methods. The results show that systems combining renewable energy with batteries can effectively reduce energy costs compared to stand-alone diesel generator sets. Stanek et al. [16] proposed a CCHP system equipped with a photovoltaic power plant and a biogas combustion engine to develop a more sustainable energy conversion system. Ruan et al. [17] proposed a novel operational strategy optimization model based on deep reinforcement learning to minimize the operational cost of an energy system consisting of CCHP, PV, and storage systems.
In the research of CCHP systems coupled with biomass energy are: Wang et al. [18] proposed co-firing of biomass and fossil energy as another way to use renewable energy in CCHP systems; Zhang et al. [19] proposed a renewable energy combined cooling, heating and electricity supply system powered by a biogas combustion engine and photovoltaic panels; Li et al. [20] proposed a novel CCHP system based on biomass gasification, which consists of a gas internal combustion engine, variable efficiency LiBr-H2O absorption refrigeration and a dehumidifying air conditioner with a dehumidifying heat exchanger. Wang et al. [21] proposed a CCHP system driven by biomass energy and assisted by solar collectors.
In the research of CCHP systems coupled with wind energy are: Xu et al. [22] proposed that CCHP system includes solar cells, diesel generators, wind turbines and backup energy storage. Buonomano et al. [23] proposed a CCHP system based on the combination of wind turbine and photovoltaic technology and coupled energy storage devices. Balali et al. [24] performed a cost and economic analysis for CCHP systems coupled with wind and solar power. Fang et al. [25] proposed an economic evaluation method for an integrated system that coupled wind energy and hydrogen energy to evaluate the economy of coupled renewable energy.
In the research of CCHP systems coupled with geothermal energy are: Kang et al. [26] proposed a new CCHP system, which is composed of a generator set, absorption chiller, heat storage tank and GSHP. Kang et al. [27] configured complementary cooling, heating, and electric organic Rankine circulation systems with ground source heat pumps to reduce variance and avoid excessive power or heat output. Ling et al. [28] comprehensively analyzed the effects of different variables on the efficiency of a CCHP system that relies on geothermal energy. Yang et al. [29] proposed that shallow geothermal energy be used as the cold source of the cooling system, which broadened the idea for the development and utilization of geothermal energy. Song et al. [30] used solar energy and geothermal energy as two kinds of renewable energy and realized the power generation of renewable energy by combining them with the power system.
Previous studies on renewable energy mainly focused on the utilization of solar, wind, geothermal, and other resources. However, there is relatively little research on the optimization of system performance. In this study, deep learning and optimization algorithms are used to further analyze the performance of CCHP systems coupled with renewable energy sources, respectively. The impact of coupled renewable energy CCHP systems on system performance under different scenarios is further investigated.
The main work of this paper on the optimization of CCHP system configuration for coupled renewable energy sources includes:
-
A CCHP system coupling solar and wind energy is constructed with the objective function of maximizing the comprehensive benefits of the system.
-
Taking energy, economic and environmental benefits as comprehensive evaluation indexes, the system multi-objective optimization algorithm is established.
-
By using a long short-term memory (LSTM) network to predict the output of renewable energy, the impact of energy uncertainty on system performance is reduced.
-
Comparison of the performance of CCHP systems coupled to PV and ST, and CCHP systems coupled to PVT for three types of buildings: office, residential, and hotel. The system performance changes with and without wind energy are further compared on this basis.
2 CCHP systems coupled with renewable energy sources
2.1 CCHP system
The structure of the CCHP system with the sub-supply system is shown in Figure 1. First, ICE consumes natural gas to supply the electrical loads of the building and the electricity required for the ground source heat pump (GSHP). The shortfall of electricity is supplemented by the grid and excess electricity is bought by the grid. In addition, the absorption units and heat exchangers are energized by recovered heat from ICE. The GSHP is employed to meet the insufficient cooling/heating loads. In a separate system, the electrical load of the building and GSHP is provided by the grid. The GSHP provides a cooling/heating load.
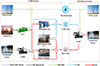 |
Fig. 1 CCHP system and separate system structure diagram. |
2.2 CCHP system coupled with solar subsystems
Solar energy can be coupled to CCHP systems in a variety of forms, such as PV, ST, and PVT. PV converts solar energy directly into electricity. ST utilizes solar heat for heating. PVT further provides dual benefits of electricity and heat by integrating photovoltaic and thermal energy conversion technologies.
2.2.1 CCHP systems coupled with PV and ST
As shown in Figure 2, first, PV is used to supply the electrical loads of the building and the electricity required for the GSHP. When electricity is low, the internal combustion engine (ICE) consumes natural gas for supplemental electricity supply. When electricity is still insufficient, it is supplemented by the grid and excess electricity is bought by the grid. In addition, the absorption unit absorbs heat generated by ST and heat generated when ICE is started to supply cooling/heating loads. The GSHP is employed to meet the insufficient cooling/heating load. In a separate system, the electrical load of the building and GSHP is provided by the grid. The GSHP provides a cooling/heating load.
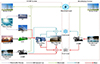 |
Fig. 2 PV and ST coupled CCHP system and separate system structure diagram. |
2.2.2 CCHP systems coupled with PVT
As shown in Figure 3, first, PVT is used to supply the electrical loads of the building and the electricity required for the GSHP. When electricity is low, ICE consumes natural gas for supplemental electricity supply. When electricity is still insufficient, it is supplemented by the grid, and excess electricity is bought by grid. In addition, the absorption unit absorbs heat generated by PVT and heat generated when ICE is started to supply cooling/heating loads. The GSHP is employed to meet the insufficient cooling/heating loads.
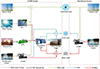 |
Fig. 3 PVT coupled CCHP system and separate system structure diagram. |
2.2.3 CCHP systems coupled with solar and wind subsystems
As shown in Figure 4, first, WT and PV are used to supply the electrical loads of the building and the electricity required for GSHP. When electricity is low, ICE consumes natural gas for supplemental electricity supply. When electricity is still insufficient, it is supplemented by the grid and excess electricity is bought by the grid. In addition, the absorption unit absorbs the heat generated by ST and the heat generated when ICE is started to supply cooling/heating loads. The GSHP is employed to meet the insufficient cooling/heating loads.
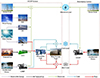 |
Fig. 4 Structural diagram of wind and solar subsystem coupled CCHP system and separate system. |
3 Mathematical models and evaluation indicators
3.1 Mathematical models
Renewable energy equipment in a CCHP system coupled with renewable energy includes: PV, ST, PVT and WT. Below are specific models of each device:
3.1.1 Mathematical model of PV
The amount of power generated by PV depends on the area laid, the solar radiation illumination and the outdoor temperature of the location.![$$ {E}_{\mathrm{PV}}={A}_{\mathrm{PV}}I{\eta }_{\mathrm{PV}}={A}_{\mathrm{PV}}I{\eta }_{\mathrm{ref}}\left[1-\beta \left({T}_b-{T}_{\mathrm{ref}}\right)+\gamma \mathrm{Log}I\right], $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq1.gif) (1)
(1)
 (2)where EPV is the amount of electricity generated by PV (kW); APV is the area of PV laid (m2); I is the amount of solar radiation in the area (W · m−2); ηPV is PV power generation efficiency (%); ηref is the efficiency of the reference module at a reference temperature Tref and solar irradiance I on the module equal to 1000 W · m−2, generally taken as 12.5%; β is the solar radiation coefficient of PV panel, typically 0.0045 °C−1; Tb is the temperature of the battery (℃); Tref is the reference temperature of the reference module, taken as 25 °C; γ is the temperature coefficient of PV, typically 0.12 °C−1; Ta is the ambient temperature (℃); To is the temperature of the battery when working underrated working condition, take 45 ℃.
(2)where EPV is the amount of electricity generated by PV (kW); APV is the area of PV laid (m2); I is the amount of solar radiation in the area (W · m−2); ηPV is PV power generation efficiency (%); ηref is the efficiency of the reference module at a reference temperature Tref and solar irradiance I on the module equal to 1000 W · m−2, generally taken as 12.5%; β is the solar radiation coefficient of PV panel, typically 0.0045 °C−1; Tb is the temperature of the battery (℃); Tref is the reference temperature of the reference module, taken as 25 °C; γ is the temperature coefficient of PV, typically 0.12 °C−1; Ta is the ambient temperature (℃); To is the temperature of the battery when working underrated working condition, take 45 ℃.
3.1.2 Mathematical model of ST
ST is converted to heat by absorbing solar energy and the heat produced is: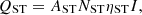 (3)
(3)
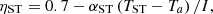 (4)where QST is the heat production of ST plate (kW); AST is the area of each ST plate, generally taken as 3.76 m2; NST is the number of slices laid on ST board; ηST is ST plate efficiency (%); αST is ST solar radiation coefficient, generally taken as 2.5 W · (m2 · k)−1; TST is ST plate temperature, which is 40 °C in winter and 70 °C in summer.
(4)where QST is the heat production of ST plate (kW); AST is the area of each ST plate, generally taken as 3.76 m2; NST is the number of slices laid on ST board; ηST is ST plate efficiency (%); αST is ST solar radiation coefficient, generally taken as 2.5 W · (m2 · k)−1; TST is ST plate temperature, which is 40 °C in winter and 70 °C in summer.
3.1.3 Mathematical model of PVT
PVT panels are a cogeneration device. It can convert solar energy into electricity and generate waste heat to provide thermal energy for the system. PVT panels generate electricity and heat as: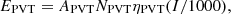 (5)
(5)
![$$ {Q}_{\mathrm{PVT}}={A}_{\mathrm{PVT}}\left[0.9\mathrm{I}\left(1-{\eta }_{\mathrm{PVT}}\right)-{\alpha }_{\mathrm{PVT}}\left({T}_{\mathrm{PVT}}-{T}_a\right)\right]/1000, $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq6.gif) (6)where EPVT is the amount of electricity generated by PVT panels (kW); APVT is the area of each PVT panel, generally taken as 1.6 m2; NPVT is the number of pieces of PVT board laid; ηPVT is PVT plate efficiency (%); QPVT is the heat production of PVT panels (kW); αPVT is the temperature coefficient of PVT plate, which is taken as 9.12 W · (m2 · k)−1; TPVT is PVT plate temperature (℃).
(6)where EPVT is the amount of electricity generated by PVT panels (kW); APVT is the area of each PVT panel, generally taken as 1.6 m2; NPVT is the number of pieces of PVT board laid; ηPVT is PVT plate efficiency (%); QPVT is the heat production of PVT panels (kW); αPVT is the temperature coefficient of PVT plate, which is taken as 9.12 W · (m2 · k)−1; TPVT is PVT plate temperature (℃).
The equations for ηPVT and TPVT are shown in (7) and (8):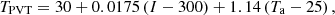 (7)
(7)
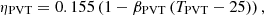 (8)where βPVT is PVT plate temperature coefficient, generally selected 0.43% · ℃−1.
(8)where βPVT is PVT plate temperature coefficient, generally selected 0.43% · ℃−1.
3.1.4 Mathematical model of WT
The performance of the WT is mainly affected by wind speed and power rating. The WT output is when the hub height is set to 36 m: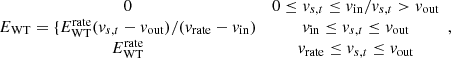 (9)where EWT is the WT generation capacity (kW);
(9)where EWT is the WT generation capacity (kW); 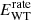 is the WT power rating, taken as 20 kW; vs,t is the wind speed (m · s−1); vout is the cut-out wind speed, set to 20 m · s−1; vrate is the rated wind speed, set at 8.5 m · s−1; vin is the cut-in wind speed, set at 2.75 m · s−1.
is the WT power rating, taken as 20 kW; vs,t is the wind speed (m · s−1); vout is the cut-out wind speed, set to 20 m · s−1; vrate is the rated wind speed, set at 8.5 m · s−1; vin is the cut-in wind speed, set at 2.75 m · s−1.
3.2 Evaluation indicators
In this study, energy benefits, economic benefits, and environmental benefits are used as comprehensive evaluation indexes of the system.
3.2.1 Energy benefit
Primary energy includes natural gas consumed by ICE and fossil energy consumed by purchased electricity. The primary energy savings rate (PESR) is calculated by the formula: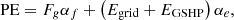 (10)
(10)
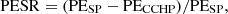 (11)where αf is the standard coal conversion factor for natural gas combustion (kJ · m−3); αe is the standard coal conversion factor (kJ · (kWh)−1) for power plant generation; Egrid is grid purchased power, excluding GSHP’s power purchased from the grid (kW); EGSHP is the power consumption (kW) for GSHP operation; PESP is the annual primary energy consumption of the separate system (kJ); PECCHP is the annual primary energy consumption of the CCHP system.
(11)where αf is the standard coal conversion factor for natural gas combustion (kJ · m−3); αe is the standard coal conversion factor (kJ · (kWh)−1) for power plant generation; Egrid is grid purchased power, excluding GSHP’s power purchased from the grid (kW); EGSHP is the power consumption (kW) for GSHP operation; PESP is the annual primary energy consumption of the separate system (kJ); PECCHP is the annual primary energy consumption of the CCHP system.
3.2.2 Economic benefit
The total annual cost includes the cost of purchased electricity, purchased gas, carbon tax and initial investment in equipment. The total annual cost is calculated by the formula: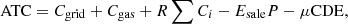 (12)
(12)
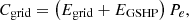 (13)
(13)
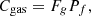 (14)where Cgrid is the grid power purchase cost, including the amount of power purchased to satisfy the electric load and EGSHP (CHY); Cgas is the cost of gas purchases (CNY); Esale is the feed-in tariff (kW); P is feed-in tariff (CNY · (kW)−1); μ is the carbon tax (CNY · (kg)−1); Pe is the grid purchase price of electricity (CNY · (kW)−1); Fg is ICE gas consumption(m3); Pf is the gas purchase price (CNY).
(14)where Cgrid is the grid power purchase cost, including the amount of power purchased to satisfy the electric load and EGSHP (CHY); Cgas is the cost of gas purchases (CNY); Esale is the feed-in tariff (kW); P is feed-in tariff (CNY · (kW)−1); μ is the carbon tax (CNY · (kg)−1); Pe is the grid purchase price of electricity (CNY · (kW)−1); Fg is ICE gas consumption(m3); Pf is the gas purchase price (CNY).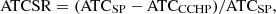 (15)where ATCSR is the annual total cost savings rate (%); ATCSP is the total annual cost of the separate system (CHY); ATCCCHP is the annual operating cost of the CCHP system(CNY).
(15)where ATCSR is the annual total cost savings rate (%); ATCSP is the total annual cost of the separate system (CHY); ATCCCHP is the annual operating cost of the CCHP system(CNY).
3.2.3 Environmental benefit
CO2 emissions include CO2 from burning natural gas and CO2 from power plants. The CO2 reduction rate is calculated as: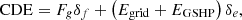 (16)
(16)
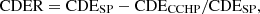 (17)where δf is the CO2 emission factor for natural gas combustion (kg · m−3); δe is the CO2 emission factor for power plant electricity generation (kg · m−3); CDER is the CO2 reduction rate(%); CDESP is the annual CO2 emissions from theseparate system (kg); CDECCHP is the annual CO2 emissions of the CCHP system.
(17)where δf is the CO2 emission factor for natural gas combustion (kg · m−3); δe is the CO2 emission factor for power plant electricity generation (kg · m−3); CDER is the CO2 reduction rate(%); CDESP is the annual CO2 emissions from theseparate system (kg); CDECCHP is the annual CO2 emissions of the CCHP system.
3.2.4 Combined benefits
Considering the influence of different performance evaluation indicators on the system, the weights of different indicators are calculated using the analytic hierarchy process (AHP). Figure 5 shows the hierarchy of composite indicators.
 |
Fig. 5 Hierarchy of composite indicators. |
The AHP obtains a judgment matrix based on the importance of the indicators. The meanings of the scales and the optimization parameters are shown in Tables 1 and 2, respectively.
AHP scale meaning.
AHP optimization parameters.
The comprehensive performance (CP) of the systems are: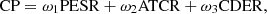 (18)where ω1 is the weight of the energy indicator; ω2 is the weight of the economy indicator; ω3 is the weight of the environment indicator. All three weights are calculated by AHP.
(18)where ω1 is the weight of the energy indicator; ω2 is the weight of the economy indicator; ω3 is the weight of the environment indicator. All three weights are calculated by AHP.
The corresponding weights of each indicator are calculated as ω1 = 0.1634, ω2 = 0.5396 and ω3 = 0.2907 respectively.
4 LSTM and optimization algorithms
There are two optimization efforts in this study: 1) LSTM-based renewable energy output prediction. 2) Multi-objective optimization based on non-dominated sorted genetic algorithm-II (NSGA-II) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS).
The multi-objective optimization process is shown in Figure 6. The NSGA-II algorithm is first used to generate the set of Pareto frontier solutions. TOPSIS is then used to calculate the distance between each solution and the ideal and anti-ideal solutions. Finally, the distance value obtained from the TOPSIS calculation is used to decide the optimal solution.
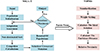 |
Fig. 6 Multi-objective optimization flowchart. |
4.1 LSTM
LSTM is a deep learning model that predicts time series data. By backpropagation and gradient descent algorithm, good performance is shown. LSTM can effectively mitigate the problem of gradient disappearance or gradient explosion by introducing a “gated cell” mechanism. LSTM cell structure consists of input gates (it), forget gates (ft), output gates (ot), and memory gates (ct). As shown in Figure 7.
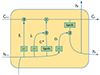 |
Fig. 7 LSTM cell structure. |
The forget gate is responsible for receiving Ct−1 and deciding which parts are retained and forgotten. It is represented by equation (19):![$$ {f}_t=\sigma \left({W}_f\cdot \left[{h}_{t-1},{X}_t\right]+{b}_f\right). $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq20.gif) (19)
(19)
The memory gate is responsible for screening new information to be stored in the cell state. It is represented by equations (20)–(22):![$$ {i}_{\mathrm{t}}=\sigma \left({W}_{\mathrm{i}}\cdot \left[{h}_{\mathrm{t}-1},{X}_{\mathrm{t}}\right]+{b}_{\mathrm{i}}\right), $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq21.gif) (20)
(20)
![$$ {{C}_t}^{\prime}=\mathrm{tanh}\left({W}_c\cdot \left[{h}_{t-1},{X}_t\right]+{b}_c\right), $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq22.gif) (21)
(21)
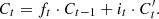 (22)
(22)
The output gate determines the output value according to the cell state. It is represented by equations (23) and (24):![$$ {o}_t=\sigma \left({W}_0\cdot \left[{h}_{t-1},{X}_t\right]+{b}_o\right), $$](/articles/stet/full_html/2024/01/stet20240073/stet20240073-eq24.gif) (23)
(23)
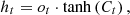 (24)where Xt is the input vector at moment t; Ct−1 is the cell state at moment t − 1; ht is the state of the cell at moment t; Ct is the hidden layer state at moment t; ht−1 is the module output at moment t − 1; σ is a sigmoid layer; ft is the output of the forget gate; Wt is the weight matrix; bf is biased; [ht−1, Xt] represents two matrices spliced together.
(24)where Xt is the input vector at moment t; Ct−1 is the cell state at moment t − 1; ht is the state of the cell at moment t; Ct is the hidden layer state at moment t; ht−1 is the module output at moment t − 1; σ is a sigmoid layer; ft is the output of the forget gate; Wt is the weight matrix; bf is biased; [ht−1, Xt] represents two matrices spliced together.
4.2 NSGA-II
The flow of NSGA-II is as follows:
-
Population initialization: Randomly generate a set of individuals. Each individual contains a set of values for the decision variables.
-
Fitness evaluation: Individual fitness is assessed and objective function values are calculated.
-
Non-dominated sorting: Based on the individual fitness value and the objective function value, the individuals are subjected to non-dominated sorting. Individuals are categorized into different non-dominated tiers that serve as domination frontiers.
-
Congestion calculation: Inter-individual congestion distances are computed in each dominant frontier.
-
Selection, crossover and mutation: A certain number of individuals are selected based on non-dominated sorting and congestion distance. Selected individuals are subjected to crossover and mutation operations to generate new individuals.
-
Renew population: The newly generated individuals and the original population are merged into a new population.
-
Repeat run: Repeat steps 2–6 until the specified termination condition is reached.
-
Output result: Extracting the Pareto Frontier from the final population. The Pareto front represents the set of optimal solutions under multiple objective functions.
The optimization parameters of NSGA-II algorithm are shown in Table 3.
NSGA-II optimized parameters.
4.3 TOPSIS
TOPSIS is a multi-criteria decision analysis method for selecting the best decision option. TOPSIS compares the distance between the decision solution and the ideal and anti-ideal solutions to determine the optimal or optimal approximate solution.
The basic steps of the TOPSIS method are as follows:
-
Standardization: identify guidelines for evaluating and comparing decisions. The performance metrics data for each decision are formed into a decision matrix and normalized.
-
Weight setting: Normalized matrix normalization. Indicator values are transformed into dimensionless relative weights.
-
Calculate the ideal solution: Ideal and anti-ideal solutions are determined based on the nature of each criterion.
-
Calculate the Euclidean distance: Calculate the Euclidean distance between each decision scheme and the ideal and anti-ideal solutions.
-
Relative closeness: the relative closeness of each decision scheme to the ideal solution is calculated based on the distance value. That is, the ratio of the distance of the decision scheme to the ideal solution to the sum of the distances to the ideal solution and the anti-ideal solution is calculated.
-
Sort: the decision options are ranked and the optimal or optimal approximate solution is determined from highest to lowest.
5 Results and discussion
5.1 Relevant data
Shijiazhuang, Hebei Province, China is in the temperate monsoon climate zone. It is hot in summer and cold in winter, and the transition season is extremely short. Figure 8 shows hourly climate change in Shijiazhuang for a typical year.
 |
Fig. 8 Hourly climate change in typical years in Shijiazhuang area. a) Outdoor temperature, b) Solar radiation, c) Wind speed. |
It can be seen from Figure 8a that outdoor temperature from May 1 to September 30 is significantly higher than other time periods. Therefore, in the following analysis, the period from May 1 to September 30 is defined as the cooling season. The rest of the year is defined as the heating season. According to Figure 8b, annual sunlight exposure ranges from 2200 to 3200 h. The average peak hours of sunlight exposure ranged from 1387 to 1854 h. Radiation levels ranged from 1393 to 1855 kWh · m−2. This creates ideal conditions for photovoltaic power generation in the Shijiazhuang area. According to Figure 8c, the maximum value of wind speed in Shijiazhuang is 12.2 m · s−1, which varies seasonally throughout the year. Between 2020 and 2030, Shijiazhuang’s developable capacity for wind power is estimated to be 2.1×106 kW, which could account for 3.33% of the province’s wind resources.
The loads of office, residential and hotel buildings are simulated using DeST software based on outdoor temperature and radiation. The results are shown in Table 4. As can be seen from Table 4, the public areas and guest rooms of hotel buildings have a higher demand, requiring longer energy use and a larger energy use area. Therefore, energy use is much higher than in office and residential buildings. Its maximum annual cooling, heating, and electrical loads are 1608.08 kW, 891.00 kW, and 220.00 kW, respectively. The cumulative cooling and heating load indicators for the year are 95.70 kW · m−2 and 83.19 kW · m−2, respectively. The cumulative cooling and heating loads for the year are 968,691 kW · m and 842,090 kW · m, respectively.
Building information.
5.2 Renewable energy output prediction
Forecasting renewable energy output scenarios can avoid the impacts of uncertainty on the CCHP system. The main influencing factors for solar and wind-powered subsystems are outdoor temperature, solar radiation and wind speed. They are predicted using LSTM. The output of PV, ST, PVT, and WT is then forecasted. Figures 9–11 show the comparison of the predicted values of outdoor temperature, solar radiation, and wind speed with the actual values and predicted errors.
 |
Fig. 9 Comparison of predicted and actual outdoor temperature values and prediction error. |
 |
Fig. 10 Comparison of predicted and actual values of solar radiation and prediction error. |
 |
Fig. 11 Comparison of wind speed prediction and actual value and prediction error. |
As shown in Figures 9–11, the predicted and actual curves show similar downward, upward and fluctuating trends. The error plots show that the error distribution is approximately normal. The root mean square error (RMSE) for outdoor temperature, solar radiation, and wind speed are 0.7337, 0.0469, and 0.3098, respectively.
Taking office buildings as an example, the output of PV, ST, PVT and WT are shown in Figure 12.
 |
Fig. 12 Comparison of actual and predicted equipment output. a) PV, b) ST, c) PVT, d) WT. |
As can be seen from Figure 12, the output forecasts of PV and ST, as well as the power generation and heating forecasts of PVT, are biased from the actual results between 6:00 and 18:00. The period when the predicted value and the actual value are significantly different is between 12:00 and 16:00. The error reaches its maximum at 15:00. The maximum error values are 14.10 kW, 27.54 kW, 6.83 kW, and 24.09 kW, respectively. The error is due to a significant decrease in solar radiation during this period. The predicted result of WT has little deviation from the actual result. The maximum error is reached at 24:00, and the maximum error value is only −1.97 kW.
The results show that the maximum error of LSTM model is 27.54 kW in the acceptable range. Therefore, applying it to day-ahead forecasting can effectively reduce the impact of renewable energy uncertainties on system performance.
5.3 Optimization of solar subsystem coupled CCHP system configuration
Figure 13 shows the Pareto frontier of the PVT-CCHP system and PV-ST-CCHP system by NSGA-II optimization.
 |
Fig. 13 Pareto frontier of the PVT-CCHP system and the PV-ST-CCHP System. |
As can be seen from Figure 13, the PESR, CDER, and ATCSR values of CCHP systems coupled to PV and ST are higher than those of CCHP systems coupled to PVT in the Pareto frontier obtained for office, residential, and hotel buildings. The results show that the Pareto frontier of the CCHP system coupled with PV and ST is better than that of the CCHP system coupled with PVT in terms of energy efficiency, environmental benefit and economic benefit. Moreover, the results of hotel buildings with two CCHP systems outperformed office buildings and residential buildings in terms of performance. To further verify results, the obtained Pareto frontiers are input into TOPSIS for decision-making. Table 5 shows the results of a comparison of equipment capacity between the PV-ST-CCHP system and the PVT-CCHP system for each building application.
Equipment capacity after TOPSIS decision.
Figure 14 shows a comparative analysis of economic, environmental and energy benefits of PV-ST-CCHP and PVT-CCHP systems for three types of buildings in this capacity configuration.
 |
Fig. 14 Performance analysis of the PVT-CCHP system vs. the PV-ST-CCHP system. |
As can be seen from Figure 14, for office, residential and hotel buildings, the ATCSR values of CCHP systems coupled with PV and ST are 4.93%, 4.15% and 5.96% higher than those coupled with PVT, respectively. The CDER values of CCHP systems coupled with PV and ST are 4.15%, 4.71% and 4.77% higher than those coupled with PVT, respectively. The PESR values of CCHP systems coupled with PV and ST are 4.60%, 5.86% and 5.87% higher than those coupled with PVT, respectively. The CP values of CCHP systems coupled with PV and ST are 4.62%, 4.57% and 5.56% higher than those coupled with PVT, respectively. The results show that the CCHP system coupled with PV and ST is better than CCHP system coupled with PVT in terms of energy benefit, environmental benefit, economic benefit and system comprehensive benefit.
5.4 Optimization of wind energy subsystem coupled CCHP system configuration
It is known that coupled PV and ST CCHP systems in three types of buildings have superior performance in terms of economy, environment, and energy. Therefore, this section further optimizes the wind subsystem coupled CCHP system based on the optimization results of the solar subsystem configuration. Figure 15 shows the Pareto frontier of the PV-ST-CCHP system and PV-ST-WT-CCHP system by NSGA-II optimization.
 |
Fig. 15 Pareto frontier for the PV-ST-WT-CCHP system vs. the PV-ST-CCHP system. |
As can be seen from Figure 15, the PESR, CDER and ATCSR values of the CCHP system coupled with PV, ST and WT are higher than those of the CCHP system coupled with PV and ST in the Pareto front obtained for office, residential and hotel buildings. The results show that the Pareto frontier of the CCHP system coupled with PV, ST and WT is better than that of the CCHP system coupled with PV and ST in terms of energy efficiency, environmental benefits, and economic benefits. Moreover, the results of hotel buildings with two CCHP systems outperformed office buildings and residential buildings in terms of performance. To further verify the results, the obtained Pareto frontiers are input into TOPSIS for decision-making. Table 6 shows a comparison of the equipment capacity of PV-ST-WT-CCHP system and PV-ST-CCHP system for each building application.
Equipment capacity after TOPSIS decision.
Figure 16 shows a comparative analysis of the economic, environmental, and energy benefits of PV-ST-WT-CCHP and PV-ST-CCHP systems for three types of buildings in this capacity configuration.
 |
Fig. 16 Performance analysis of the PV-ST-WT-CCHP system and the PV-ST-CCHP system. |
As can be seen from Figure 16, the ATCSR values of CCHP systems coupled with PV, ST and WT are 1.14%, 0.54% and 0.14% higher than those coupled with PV and ST, respectively, for office, residential and hotel buildings. CCHP systems coupled with PV, ST and WT have 1.46%, 0.69% and 0.51% higher CDER values than those coupled with PV and ST, respectively. The PESR values of CCHP systems coupled with PV, ST and WT are 1.85%, 0.82% and 0.59% higher than those coupled with PV and ST, respectively. The CP values of CCHP systems coupled with PV, ST and WT are 1.34%, 0.62% and 0.32% higher than those coupled with PV and ST, respectively. The results show that with the addition of coupled wind energy, the proportion of renewable energy increases. This makes CCHP system coupled with PV, ST and WT better than CCHP system coupled with PV and ST in terms of energy efficiency, environmental benefit, economic benefit and system comprehensive benefit.
6 Conclusion
A method based on the combination of LSTM and optimization algorithm is proposed for three types of buildings, office, residential and hotel, in Shijiazhuang area. The economic, environmental and energy performance of the CCHP system with coupled solar and wind subsystems are analyzed separately:
-
CCHP systems coupled with renewable energy sources can increase the energy efficiency of the system and reduce pollutant emissions. By integrating renewable energy sources such as solar and wind, the system to be more flexible in terms of energy supply. It also effectively reduces dependence on conventional energy sources, thereby improving the overall energy utilization efficiency of the system.
-
LSTM models can be applied to day-ahead forecasting to reduce the impact of renewable energy uncertainty on system performance. Its powerful time series analysis capabilities can better capture and understand the volatile nature of renewable energy production. The impact of such fluctuations on system operation is effectively minimized.
-
The performance of the CCHP system coupled to PVT is lower than that of the CCHP system coupled to PV and ST. It shows that independently heated and powered devices are more effective than PVT. This may be because stand-alone PV and ST systems perform better in terms of capacity and efficiency in a given situation. Perhaps the dual utilization of PVT systems in terms of heat and power conversion has not been as effective as expected under certain environmental conditions. Resulting in less overall performance than PV and ST systems.
-
The system performance of the CCHP system coupled with PV and ST can be further improved by adding wind energy. The solar subsystem has already injected some energy into the system. With the addition of wind energy, the system is more flexible in terms of energy supply and is better able to adapt to changes in energy sources under different environmental conditions.
References
- Wang Y.Z., Kang L.G., Zhang J., Zhao W., Zhu Y.L., Zhao J. (2021) Development history, typical from and future trend of integrated energy system, Acta Energ. Sol. Sin. 42, 8, 84–95. [Google Scholar]
- Yu L.S., Zeng Y., Li N.F., Wang B., Zhang S.R., Li H. (2023) Optimization of combined cooling, heating and power system using clean energy for low-carbon communities, Build. Sci. 39, 6, 197–205. [Google Scholar]
- Liu Y.R., Zhang R.P., Dong H.Y. (2023) Optimal scheduling of integrated energy systems in agricultural parks based on improved probability planning algorithm, Integr. Intell. Energy 45, 10, 35–43. [Google Scholar]
- Liu M., Shi Y., Fang F. (2014) Combined cooling, heating and power systems: A survey, Renew. Sustain. Energy Rev. 35, 1–22. [CrossRef] [Google Scholar]
- Lin J.H., Xi S.Y., Li M.S., Wu Q.H. (2023) Multi-time scales optimization of park-level integrated energy system, Mod. Electron. Tech. 46, 22, 137–143. [Google Scholar]
- Gao Y.F., Yun C.B., Kong F.P., Wang X.S. (2023) Optimization of integrated energy system coupled with power-to-gas and carbon capture equipment under demand response incentive, Electric Power 57, 1–9. [Google Scholar]
- Gao P.H., Dai Y.J., Tong Y.W., Dong P.W. (2015) Energy matching and optimization analysis of waste to energy CCHP (combined cooling, heating and power) system with exergy and energy level, Energy 79, 522–535. [CrossRef] [Google Scholar]
- Maraver D., Sin A., Royo J., Sebastian F. (2013) Assessment of CCHP systems based on biomass combustion for small-scale applications through a review of the technology and analysis of energy efficiency parameters, Appl. Energy 102, 1303–1313. [CrossRef] [Google Scholar]
- Ma D., Zhang L., Sun B. (2021) An interval scheduling method for the CCHP system containing renewable energy sources based on model predictive control, Energy 236, 121418. [CrossRef] [Google Scholar]
- Jia J.D., Chen H.W., Liu H.T., Ai T.C., Li H.Q. (2021) Thermodynamic performance analyses for CCHP system coupled with organic Rankine cycle and solar thermal utilization under a novel operation strategy, Energy Convers. Manag. 239, 114212. [CrossRef] [Google Scholar]
- Soheyli S., Mayam M.H.S., Mehrjoo M. (2016) Modeling a novel CCHP system including solar and wind renewable energy resources and sizing by a CC-MOPSO algorithm, Appl. Energy 184, 375–395. [CrossRef] [Google Scholar]
- Ren F., Wei Z., Zhai X. (2021) Multi-objective optimization and evaluation of hybrid CCHP systems for different building types, Energy 215, 119096. [CrossRef] [Google Scholar]
- Ge Y., Han J.T., Ma Q.Z., Feng J.H. (2022) Optimal configuration and operation analysis of solar-assisted natural gas distributed energy system with energy storage, Energy 246, 123429. [CrossRef] [Google Scholar]
- Hassan R., Das B.K., Al-Abdeli Y.M. (2022) Investigation of a hybrid renewable-based grid-independent electricity-heat nexus: impacts of recovery and thermally storing waste heat and electricity, Energy Convers. Manag. 252, 115073. [CrossRef] [Google Scholar]
- Huneke F., Henkel J., Gonzale J.A.B., Erdmann G. (2012) Optimisation of hybrid off-grid energy systems by linear programming, Energy Sustain. Soc. 2, 1, 1–19. [Google Scholar]
- Stanek W.W., Gazda W., Kostowski W. (2015) Thermo-ecological assessment of CCHP (combined cold-heat-and-power) plant supported with renewable energy, Energy 92, Part 3, 279–289. [CrossRef] [Google Scholar]
- Ruan Y.J., Liang Z.Y., Qian F.Y., Meng H., Gao Y. (2023) Operation strategy optimization of combined cooling, heating, and power systems with energy storage and renewable energy based on deep reinforcement learning, J. Build. Eng. 65, 105682. [CrossRef] [Google Scholar]
- Wang J.J., Mao T.Z., Sui J., Jin H.G. (2015) Modeling and performance analysis of CCHP (combined cooling, heating and power) system based on co-firing of natural gas and biomass gasification gas, Energy 93, Part 1, 801–815. [CrossRef] [Google Scholar]
- Zhang L., Li F., Sun B., Zhang C. (2019) Integrated optimization design of combined cooling, heating, and power system coupled with solar and biomass energy, Energies 12, 687. [CrossRef] [Google Scholar]
- Li X., Kan X., Sun X., Zhao Y., Ge T., Dai Y. (2019) Performance analysis of a biomass gasification-based CCHP system integrated with variable-effect LiBr-H2O absorption cooling and desiccant dehumidification, Energy 176, 961–979. [CrossRef] [Google Scholar]
- Wang Y., Feng H. (2019) Optimization of capacity of CCHP system coupled with solar and biomass energy, IOP Conf. Ser. Earth Environ. Sci. 371, 4, 042030. [CrossRef] [Google Scholar]
- Xu B., Wang J. (2024) Optimal energy optimization of the integrated hybrid energy system considering storage system performance, Multiscale Multidiscip. Model. Exp. Des. 7, 2, 705–710. [CrossRef] [Google Scholar]
- Buonomano A., Calise F., Vicidomini M. (2018) A hybrid renewable system based on wind and solar energy coupled with an electrical storage: dynamic simulation and economic assessment, Energy 155, 174–189. [CrossRef] [Google Scholar]
- Balali M.H., Nouri N., Omrani E., Nasiri A., Otieno W. (2017) An overview of the environmental, economic, and material developments of the solar and wind sources coupled with the energy storage systems, Int. J. Energy Res. 41, 1948–1962. [CrossRef] [Google Scholar]
- Fang R. (2019) Life cycle cost assessment of wind power–hydrogen coupled integrated energy system, Int. J. Hydrog. Energy 44, 29399–29408. [CrossRef] [Google Scholar]
- Kang L., Yang J., Deng S. (2016) Energy, economical, environmental evaluation of a CCHP-GSHP system based on carbon tax and electric feed in tariff, Energy Proc. 88, 510–517. [CrossRef] [Google Scholar]
- Kang L., Yang J., An Q., Deng S., Zhao J., Li Z. (2017) Complementary configuration and performance comparison of CCHP-ORC system with a ground source heat pump under three energy management modes, Energy Convers. Manag. 135, 244–255. [CrossRef] [Google Scholar]
- Ling W., Abed M.A., Farouk N. (2024) Modeling of geothermal tailored CCHP system with heat recovery centered thermal design/analysis; ANN-based optimization and economic study, Case Stud. Therm. Eng. 59, 104511. [CrossRef] [Google Scholar]
- Yang J., Song W., Wang Z. (2024) Direct/indirect optimal use of shallow geothermal energy in floor radiant cooling system coupled with air-handling system, J. Build. Eng. 89, 109206. [CrossRef] [Google Scholar]
- Song A., Zhu J., Zhang P. (2019) Experimental research on solar and geothermal energy coupling power generation system, Energy Proc. 158, 5982–5987. [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 CCHP system and separate system structure diagram. |
| In the text | |
 |
Fig. 2 PV and ST coupled CCHP system and separate system structure diagram. |
| In the text | |
 |
Fig. 3 PVT coupled CCHP system and separate system structure diagram. |
| In the text | |
 |
Fig. 4 Structural diagram of wind and solar subsystem coupled CCHP system and separate system. |
| In the text | |
 |
Fig. 5 Hierarchy of composite indicators. |
| In the text | |
 |
Fig. 6 Multi-objective optimization flowchart. |
| In the text | |
 |
Fig. 7 LSTM cell structure. |
| In the text | |
 |
Fig. 8 Hourly climate change in typical years in Shijiazhuang area. a) Outdoor temperature, b) Solar radiation, c) Wind speed. |
| In the text | |
 |
Fig. 9 Comparison of predicted and actual outdoor temperature values and prediction error. |
| In the text | |
 |
Fig. 10 Comparison of predicted and actual values of solar radiation and prediction error. |
| In the text | |
 |
Fig. 11 Comparison of wind speed prediction and actual value and prediction error. |
| In the text | |
 |
Fig. 12 Comparison of actual and predicted equipment output. a) PV, b) ST, c) PVT, d) WT. |
| In the text | |
 |
Fig. 13 Pareto frontier of the PVT-CCHP system and the PV-ST-CCHP System. |
| In the text | |
 |
Fig. 14 Performance analysis of the PVT-CCHP system vs. the PV-ST-CCHP system. |
| In the text | |
 |
Fig. 15 Pareto frontier for the PV-ST-WT-CCHP system vs. the PV-ST-CCHP system. |
| In the text | |
 |
Fig. 16 Performance analysis of the PV-ST-WT-CCHP system and the PV-ST-CCHP system. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




