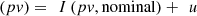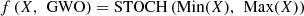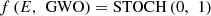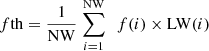| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 8 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.2516/stet/2024002 | |
| Published online | 06 February 2024 | |
Regular Article
EPCMSDB: Design of an ensemble predictive control model for solar PV MPPT deployments via dual bioinspired optimizations
VIT-AP University, 119-Central Block, Amravati 522237 Adhara Pradesh, India
* Corresponding author: agam.goswami@vitap.ac.in
Received:
25
May
2023
Accepted:
9
January
2024
With the increasing demand for renewable energy, solar power has emerged as a promising option for sustainable power generation. However, the effectiveness and efficiency of solar power systems rely on the ability to effectively manage their performance, making it essential to develop efficient control models. This paper proposes a novel ensemble predictive control model for solar deployments using bio-inspired optimizations to improve load-connected solar deployments’ performance. The proposed model integrates multiple control devices, including Maximum Power Point Tracker, Proportional-Integral-Derivative, Proportional-Integral, and Fuzzy Logic Controllers, to selectively control the solar Photovoltaic systems. The proposed model incorporates a predictive control operation utilizing an LSTM-GRU (Long Short-Term Memory-Gated Recurrent Unit) with the VARMA (Vector Auto-Regressive Moving Average) model, which can accurately predict the future power generation of the solar system. This feature can facilitate efficient energy management and increase the system’s performance for different use cases. Implement a SEPIC (Single Ended Primary Inductor Capacitor) converter design to improve the system’s overall efficiency levels. To validate the effectiveness of the proposed approach, the author conducted experiments using real-world data and compared the proposed results with other control strategies. The results demonstrate that the ensemble predictive control model based on bio-inspired optimizations outperforms the existing control models regarding accuracy, efficiency, and stability levels. The proposed model has the potential to significantly improve the performance of load-connected solar deployments, offering a more practical approach to solar power generation. The combination of predictive control operations with bio-inspired optimizations can facilitate the design of sustainable energy systems with higher efficiency and accuracy.
Key words: Solar Power / MPPT / PI / PID / Fuzzy / VARMA / LSTM / GRU
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abbreviations
MPPT: Maximum Power Point Tracker
PID: Proportional-Integral-Derivative
SEPIC: Single Ended Primary Inductor Capacitor
VARMA: Vector Auto-Regressive Moving Average
CSSI: Control Signal Smoothness Index
WPI: Weighted Performance Index
1 Introduction
In recent years, solar power has emerged as a promising option for sustainable power generation due to its environmental benefits and cost-effectiveness. The growing demand for renewable energy sources has led to an increase in the deployment of solar power systems, especially in load-connected applications [1]. However, the effectiveness and efficiency of solar power systems rely on effectively managing their performance [2], which makes it essential to develop efficient control models [3]. The author proposes a novel ensemble predictive control model for solar deployments using dual bio-inspired optimizations. Proposed model integrates multiple control devices, including Maximum Power Point Tracking (MPPT), Proportional-Integral-Derivative (PID), Proportional-Integral (PI), and Fuzzy Logic Controllers (FLC) [4], which are selectively controlled by a bio-inspired optimization technique to determine the optimal parameters and configurations [5]. Furthermore, Model incorporates a predictive control operation using a VARMA-GRU (Vector Auto-regressive Moving Average-Gated Recurrent Unit) with an LSTM (Long Short-Term Memory) model to accurately predict future power generation, which can facilitate more efficient energy management capabilities [6].
The proposed model offers a more comprehensive and efficient approach to control, significantly improving the performance of load-connected solar deployments. The author conducts experiments using real-world data to demonstrate the effectiveness of the proposed model compared to existing control strategies.
The remainder of this paper is organized as follows:
-
Section 2 provides an overview of the related work in the area of solar power control models.
-
Section 3 presents the proposed ensemble predictive control model, including the dual bio-inspired optimization technique, control devices, and predictive control operation.
-
Section 4 details the result in analysis and comparison.
-
Finally, conclude the paper in Section 5 with a summary of our findings and future work recommendations.
2 Review of existing control model
The optimization of solar power systems has been an active area of research in recent years due to the increasing demand for renewable energy sources [7]. Various control strategies have been proposed to improve the performance and efficiency of load-connected solar deployments [8, 9]. In this section, the author reviews some related work in solar power control models [10–12].
-
Fuzzy Logic Controllers (FLC) [22] have also been proposed for solar power systems [23, 24]. Fuzzy controllers use linguistic variables and rules to control the system, making them more robust to disturbances and noise than PID controllers. Fuzzy controllers [25] have been shown to improve the efficiency and performance of solar power systems [26].
-
Predictive control is another approach that has gained attention in recent years for different use cases [27, 28]. Predictive control methods use a model of the system to predict future behavior and optimize the control input accordingly for different scenarios [29]. The predictive control approach [30], has been shown to improve the performance of solar power systems, especially in situations with varying weather conditions [31, 32].
-
Bio-inspired optimization techniques have also been proposed for solar power systems [33]. These methods use algorithms to maximize available power from the solar panels by varying the duty cycle of the converters [14]. Various MPPT algorithms have been proposed, including Perturb.
-
MPPT is one of the most widely used control techniques for solar power systems [13]. MPPT methods aim to extract the maximum available power from the solar panels by varying the duty cycle of the converters.
-
PID controllers are another commonly used control technique for solar power systems Incremental Conductance (INC) [16], and Fractional Open Circuit Voltage (FOCV) [18]. PID controllers aim to maintain the output voltage or current at a desired value by adjusting the converter’s duty cycle based on the error between the desired and measured values and samples [19]. However, PID controllers are susceptible to noise and disturbances [20], which can affect their performance levels [21]. ired by natural processes, such as genetic algorithms, particle swarm optimization, and ant colony optimization, to optimize the control Perturb and Observe (P&O) [15, 17], among others parameters of the systems [34, 35]. Bio-inspired optimization techniques have been shown to improve the performance [36] and efficiency of solar power systems [37, 38].
This proposes a novel ensemble predictive control model for solar deployments [39, 40] using dual bio-inspired optimizations [41]. Our proposed model integrates multiple control devices, including MPPT, PID, PI, and Fuzzy controllers [42], which are selectively controlled [43] by a bio-inspired optimization technique to determine the optimal parameters and configurations [44]. Our model incorporates a predictive control operation using a VARMA-GRU with an LSTM model to predict future power generation accurately. The proposed model offers a more comprehensive and efficient control approach [45], significantly improving the performance of load-connected solar deployments [46].
3 Proposed design of an ensemble predictive control model for solar deployments via dual bio-inspired optimizations
As per the review of existing models for predictive control model for solar deployments, it can be observed that existing models are either highly complex or have lower efficiency for real-time scenarios. To overcome these issues, this text proposes designing an efficient novel ensemble predictive control model for solar deployments using dual bio-inspired optimizations, aiming to improve load-connected solar deployments’ performance. The author proposes a novel ensemble predictive control model for solar deployments using dual bio-inspired optimizations in this section. As per the flow of the model in Figure 1, it can be observed that the proposed model integrates multiple control devices, including [47],
-
MPPT,
-
PID,
-
PI,
-
FLC.
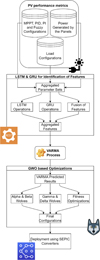 |
Fig. 1 Design of the proposed model for optimization of Solar PV Deployments. |
To selectively control the solar PV systems [48, 49]. The suggested bio-inspired optimization strategy establishes each control device’s ideal parameters and configurations, making device control more comprehensive and efficient for varied scenarios. Moreover, the proposed model incorporates a predictive control operation utilizing a VARMA-GRU with LSTM method, which can accurately predict the future power generation of the connected solar PV systems. This feature can facilitate efficient energy management and increase the system’s performance for different use cases. Additionally, the researcher implements a SEPIC (Single Ended Primary Inductor Capacitor) converter design to improve the system’s overall efficiency levels. This section is segregated into different sub-sections to elaborate on the proposed design. Each sub-section describes a different component of the design process.
3.1 Conversion of collected samples into multi-modal feature sets
The proposed model uses a fusion of LSTM and GRU for converting the collected configurations of power, load, and controller parameters into multi-modal feature sets. Variables of LSTM are:
-
Cell State (Ct)
It is a memory of LSTM.
-
Hidden State (ht)
It is an output of LSTM. It is a combination of current input (Xt) and cell state (Ct)
-
Tan h Function (tan h)
It is used to regulate/Squish the values between 1 and −1.
-
Sigmoid Function (δ)
It is used to regulate/Squish the value between 0 and 1. Sigmoid is used to Update or forget data. If the value is zero then it is used for the forgotten value. (It considers it as not important data). If the value is 1 then it is used for Kept as it is value (It considers it as important data). Values come out from Sigmoid between 0 and 1. The closer to 0 means to Forget. The closer to 1 means Kept.
There are three different gates that regulate the information flow in LSTM.
-
Forget Gate (ft): This gate decides what information should be thrown away or kept. The forget gate is a combination of the previous hidden state (ht − 1) and current input (Xt).
-
Input Gate (It): This gate decides what information should be updated or not updated. The input gate is a combination of the hidden state (ht − 1) and current input (Xt). The input gate is multiplication with the candidate cell (Ct).
-
Output Gate (Ot): This gate decides what the next hidden state should be. The output gate is a combination of the previous hidden state (ht − 1) and current input (Xt). The input gate is multiplication with tan h (C t ).
Similarly, GRU also has various components such as: especially GRU has two extra gates:
-
Reset gate (rt): The reset gate is used to decide how much past information to forget.
-
Update Gate (Ut): The update gate is used to decide what information to add or throw/remove.
The process of this conversion is iterative and can be observed in Figure 2.
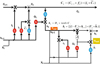 |
Fig. 2 Conversion of power, control, and load parameters into multi-modal feature sets. |
To perform this conversion, all the collected feature sets are initially represented by an input feature vector (i), which is estimated via equation (1):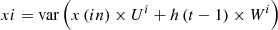 (1)where x(in) is a collection of input feature samples, U and W represent constants of the LSTM process, while h represents the kernel matrix, which must be tuned for maximization of variance levels. These levels are estimated via equation (2):
(1)where x(in) is a collection of input feature samples, U and W represent constants of the LSTM process, while h represents the kernel matrix, which must be tuned for maximization of variance levels. These levels are estimated via equation (2):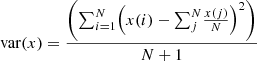 (2)where N is the total count of input samples. Similar to the input vector, a set of three different vectors, namely functional (f), output (o), and convolutional (c) features, are also estimated via equations (3)–(5) as follows:
(2)where N is the total count of input samples. Similar to the input vector, a set of three different vectors, namely functional (f), output (o), and convolutional (c) features, are also estimated via equations (3)–(5) as follows: (3)
(3)
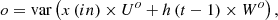 (4)
(4)
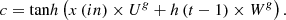 (5)
(5)
All these operators are fused to estimate an augmented temporal feature vector via equation (6), (6)
(6)
Based on these feature sets, the kernel matrix is updated via equation (7),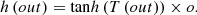 (7)
(7)
These features are further processed via equations (8) and (9), where an augmented set of forgetting (z) and retaining (r) features are estimated as follows,![$$ z=\mathrm{var}\left(W(z)\times \left[h\left({out}\right)\times T\left({out}\right)\right]\right) $$](/articles/stet/full_html/2024/01/stet20230110/stet20230110-eq8.gif) (8)
(8)
![$$ r=\mathrm{var}\left(W(r)\times \left[h\left({out}\right)\times T\left({out}\right)\right]\right). $$](/articles/stet/full_html/2024/01/stet20230110/stet20230110-eq9.gif) (9)
(9)
These vectors are fused via equations (10) and (11) to identify output feature vector sets.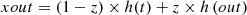 (10)
(10)
![$$ h(t)=\mathrm{tan}h\left(W\times \left[r\times h\left({out}\right)\times \enspace {T}\left({out}\right)\right]\right). $$](/articles/stet/full_html/2024/01/stet20230110/stet20230110-eq11.gif) (11)
(11)
The value of h(t) is used to iteratively calculate LSTM features, which are used to calculate GRU features. This process is repeated till the convergence criteria of equation (12) are satisfied, (12)
(12)
After condition (12) is satisfied, the process converges, and selected features are used to predict PV outputs. An error of less than 1% is ideally used for matching these value sets. These outputs are predicted by a VARMA Model, which is discussed in the next section of this text.
3.2 Design of the VARMA model for prediction of PV outputs
VARMA (Vector Auto-regressive Moving Average) models are commonly used in time-series analysis and forecasting, including for predicting Photovoltaic (PV) outputs. To perform this task, the proposed model uses a fusion of VARMA(p, q) with VARMAX(p, q) models. The VARMA(p, q) The model is represented via equation (13),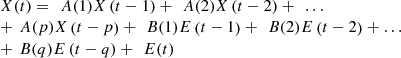 (13)where X(t) is a vector of p time-series variables, in this case, the temporal LSTM and GRU PV outputs and features. A(1), A(2), …, A(p) are p × p matrices of coefficients that measure the impact of X(t − i) on X(t), where i = 1, 2, …, p
(13)where X(t) is a vector of p time-series variables, in this case, the temporal LSTM and GRU PV outputs and features. A(1), A(2), …, A(p) are p × p matrices of coefficients that measure the impact of X(t − i) on X(t), where i = 1, 2, …, p
 while B(1), B(2), …, B(q) are p × p matrices of coefficients that measure the impact of the q past forecast errors (E(t − 1), E(t − 2), …, E(t − q)) on X(t), E(t) is a vector of white noise error terms, assumed to be normally distributed with mean zero and constant variance levels. Similarly, the VARMAX(p, q) model is represented via equation (14),
while B(1), B(2), …, B(q) are p × p matrices of coefficients that measure the impact of the q past forecast errors (E(t − 1), E(t − 2), …, E(t − q)) on X(t), E(t) is a vector of white noise error terms, assumed to be normally distributed with mean zero and constant variance levels. Similarly, the VARMAX(p, q) model is represented via equation (14),![$$ \begin{array}{c}X(t)=\enspace f\left(X,\enspace \mathrm{GWO}\right)\times \left[\begin{array}{ll}& A(1)X\left(t-1\right)+\enspace \\ & A(2)X\left(t-2\right)+\enspace \\ & \dots \enspace +\enspace A(p)\mathrm{X}\left(t-p\right)\\ & \end{array}\right]+\\ f\left(E,\enspace \mathrm{GWO}\right)\times \left[\begin{array}{ll}& B(1)\mathrm{E}\left(t-1\right)+\enspace \\ & B(2)\mathrm{E}\left(t-2\right)+\enspace \\ & \dots \enspace +\enspace B(q)E\left(t-\mathrm{q}\right)\\ & \end{array}\right]+\\ C\left(\mathrm{z}\right)+\enspace E(t)\end{array} $$](/articles/stet/full_html/2024/01/stet20230110/stet20230110-eq15.gif) (14)where C is a vector of constants that capture the long-term trend or other factors that affect the PV outputs, and z is a vector of exogenous variables (such as weather data or other factors that may affect PV outputs) that are included in the model via LSTM and GRU feature sets. Based on output value X(t), the MPTT, PID, PI, and Fuzzy controllers are deployed, f(X, GWO) and f(E, GWO) represent the tuning factors for X and E variable sets, which are extracted via GWO operations. To perform these control tasks, an augmented set of controllers is needed, each of which is discussed in the following sub-section of this text.
(14)where C is a vector of constants that capture the long-term trend or other factors that affect the PV outputs, and z is a vector of exogenous variables (such as weather data or other factors that may affect PV outputs) that are included in the model via LSTM and GRU feature sets. Based on output value X(t), the MPTT, PID, PI, and Fuzzy controllers are deployed, f(X, GWO) and f(E, GWO) represent the tuning factors for X and E variable sets, which are extracted via GWO operations. To perform these control tasks, an augmented set of controllers is needed, each of which is discussed in the following sub-section of this text.
3.3 Design of different controllers
-
MPPT is a technique used to optimize the power output of PV systems by finding and maintaining the maximum power point (MPP) of the PV array. Different control algorithms can be used for MPPT, but one common approach is using a Perturb and Observe (P&O) algorithm, which works as per the following operations.
1. Calculate the PV power via equation (15),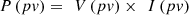 (15)
(15)
where,
P(pv) is the power generated by the PV array,
V(pv) is the PV voltage, and I(pv) represents the PV current levels.
2. Perturb the PV voltage via equation (16),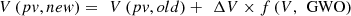 (16)
(16)
where,
V(pv, new) is the new PV voltage,
V(pv, old) is the previous PV voltage,
ΔV is a small increment in the PV voltage,
f(V, GWO) represents the voltage tuning factor which is decided by the GWO process.
3. Measure the new PV power via equation (17),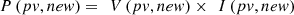 (17)
(17)
where,
I(pv, new) are the new PV current levels.
4. Calculate the power change via equation (18),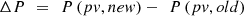 (18)
(18)
where,
P(pv, old) represents the previous PV power levels.
5. Determine the scope of the power change as follows,
If ΔP > 0, the perturbation was in the proper scope (toward the MPP), and the voltage should be increased further, while if ΔP < 0, the perturbation was in the wrong scope (away from the MPP), and the voltage should be decreased for different input types.
6. Adjust the PV voltage via equation (19),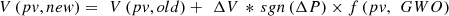 (19)where, sgn() is the sign function, which returns −1 for negative values and +1 for positive values under real-time scenarios, while f(pv, GWO) is the optimization constant for pv which is tuned via GWO operations.
(19)where, sgn() is the sign function, which returns −1 for negative values and +1 for positive values under real-time scenarios, while f(pv, GWO) is the optimization constant for pv which is tuned via GWO operations.
7. Repeat steps 2–6 until the MPP is reached for different input types.
The above equations can be implemented in a micro-controller or a dedicated MPPT controller to continuously track the MPP of the PV array and maximize the power outputs.
-
Similarly, PID control is a commonly used feedback control strategy in many industrial applications, including PV systems. The following operations do this,
Figure 3 work flow can be implemented in a microcontroller or a dedicated PID controller to regulate the PV voltage and maintain it at the desired set points. Kp, Ki, and Kd gains can be tuned based on the system dynamics and the desired performance levels.
-
PI control is a feedback control strategy commonly used in PV systems to regulate the PV voltage and maintain it at an augmented set of desired set points. This works as per the following operations,
 |
Fig. 3 PID controller work flow chart. |
Figure 4 processes were implemented on a micro-controller to regulate and maintain the PV voltage at the desired set points. The gains Kp and Ki were tuned based on the GWO Operations based on the system dynamics and the desired performance levels. PI control is more superficial than PID control, but it may not provide enough damping for systems with high dynamics or disturbances.
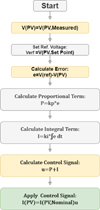 |
Fig. 4 PI controller work flow chart. |
• Similarly, Fuzzy control, a type of feedback control strategy that uses fuzzy logic to regulate the PV voltage in photovoltaic PV systems, is also used to perform control operations. This process works via the following operations,
-
Define the input variables sets,
-
PV voltage error (e).
-
Change in PV voltage error
 .
.
-
-
Define the output variable for control operations,
-
A control signal (u).
-
-
Define the fuzzy sets for the input variables under real-time scenarios,
-
PV voltage error: Negative Large (NL), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Large (PL).
-
Change in PV voltage error: Negative (N), Zero (Z), Positive (P).
-
-
Define the fuzzy sets for the output variables under different conditions,
-
Control signal: Negative Large (NL), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Large (PL).
-
-
Define the fuzzy rules as follows,
-
If e is NL and
 is N, then u is PL.
is N, then u is PL. -
If e is NL and
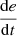 is Z, then u is PM.
is Z, then u is PM. -
If e is NL and
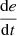 is P, then u is PS.
is P, then u is PS. -
If e is NM and
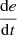 is N, then u is PM.
is N, then u is PM. -
If e is NM and
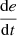 is Z, then u is PS.
is Z, then u is PS. -
If e is NM and
 is P, then u is Z.
is P, then u is Z. -
If e is NS and
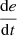 is N, then u is PS.
is N, then u is PS. -
If e is NS and
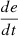 is Z, then u is Z.
is Z, then u is Z. -
If e is NS and
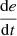 is P, then u is NS.
is P, then u is NS. -
If e is Z and
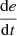 is N, then u is PS.
is N, then u is PS. -
If e is Z and
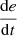 is Z, then u is Z.
is Z, then u is Z. -
If e is Z and
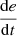 is P, then u is NS.
is P, then u is NS. -
If e is PS and
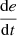 is N, then u is Z.
is N, then u is Z. -
If e is PS and
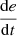 is Z, then u is NS.
is Z, then u is NS. -
If e is PS and
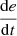 is P, then u is NM.
is P, then u is NM. -
If e is PM and
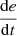 is N, then u is NS.
is N, then u is NS. -
If e is PM and
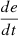 is Z, then u is NM.
is Z, then u is NM. -
If e is PM and
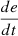 is P, then u is NL.
is P, then u is NL. -
If e is PL and
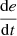 is N, then u is NM.
is N, then u is NM. -
If e is PL and
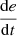 is Z, then u is NL.
is Z, then u is NL. -
If e is PL and
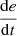 is P, then u is NL.
is P, then u is NL.
-
-
Apply the fuzzy inference method to determine the control signals
-
Determine the degree of membership of the input variables in their respective fuzzy sets using the membership functions.
-
Apply the fuzzy rules to determine the degree of membership of the output variable in its fuzzy sets using the minimum operator for the AND operation and the maximum operator for the OR operation.
-
Defuzzify the output variable to obtain a crisp value for the control signal using a defuzzification method such as the centroid or the max-average method.
-
-
Apply the control signal via equation (20),
where,
I(pv) is the PV current,
I(pv, nominal) is the nominal PV current,
u is the set of control signals.
Thus, MPPT, PID, PI, and fuzzy PV control can be expressed by defining the input and output variables, fuzzy sets, fuzzy rules, fuzzy inference methods, and control signal operations. The control signal is obtained by applying the fuzzy logic to the input variables and the fuzzy rules and then defuzzifying the output variable sets. The control signal is then added to the nominal PV current to generate the actual PV current levels. The internal constants of these controllers are tuned by a GWO-based optimization process, which is discussed in the next section of this article.
3.4 Design of the GWO model for optimizing these controllers
Once the LSTM, GRU, and VARMA Models have selected the control operations, an efficient GWO-based optimization model is used to identify optimal tuning constants. These constants are estimated via the following process.
-
Initially, an augmented set of NW Wolves is generated, each of which contains stochastic values of control constants.
-
These control constants are estimated via equations (21)–(25) as follows,
where,
Min(X) and Max(X) represents minimum and maximum values for X,
Min(V) and Max(V) represents minimum and maximum output voltage levels,
Min(P) and Max(P) represents minimum and maximum power values for individually connected loads,
while STOCH represents a stochastic process.
-
Using these values, the VARMA, GRU, and LSTM processes are executed, along with the control operations, and a SEPIC Converter is used for simulations. Converter design can be observed in Figure 5, where different circuit components are displayed along with respective load sets.
-
Based on the execution, Wolf fitness is estimated via equation (26),
 |
Fig. 5 The SEPIC converter used for simulation operations. |
where,
EER represents the Energy Efficiency Ratio and is estimated via equation (27),
CSP represents the Cost Savings Percentage and is estimated via equation (28),
CSSI represents the Control Signal Smoothness Index and is represented via equation (29),
WPI represents the Weighted Performance Index and is estimated via equation (30),
TS represents the Settling Time, and is the time taken for the system output to settle within a specified range around the desired set-points,
RI represents the Robustness Index and is estimated via equation (31) as follows,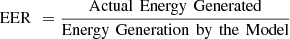 (27)
(27)
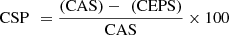 (28)where, CAS is the Cost with Alternative Strategy, while CEPS is the Cost with Ensemble Predictive Control operations.
(28)where, CAS is the Cost with Alternative Strategy, while CEPS is the Cost with Ensemble Predictive Control operations.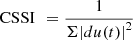 (29)where, du(t) is the change in control action at timestamp t for different input scenarios.
(29)where, du(t) is the change in control action at timestamp t for different input scenarios.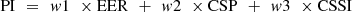 (30)where w1, w2, and w3 are weights assigned to each performance parameter for different input conditions.
(30)where w1, w2, and w3 are weights assigned to each performance parameter for different input conditions.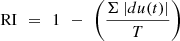 (31)where T is the total simulation time for different simulation use cases.
(31)where T is the total simulation time for different simulation use cases.
-
This fitness is estimated for each of the Wolves, and based on these fitness levels, a fitness threshold is estimated via equation (32),
where LW is the Learning Rate for different Wolves and is tuned as per their types.
• Based on this threshold, Wolves are Marked as per the following conditions,
– If fw > 2 × fth, then Wolf is marked as “Alpha” and is used to train “Beta” Wolf Sets.
– If fw > fth, then Wolf is marked as “Beta” and is used to train “Gamma” Wolf Sets. The learning rate of these Wolves is tuned via equation (33), (33)
(33)
– If fw > LW × fth, then Wolf is marked as “Gamma” and is used to train “Delta” Wolf Sets. The learning rate of these Wolves is tuned via equation (34),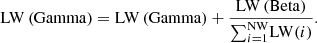 (34)
(34)
– Other Wolves are Marked as “Delta”, and their learning rate is modified via equation (35), (35)
(35)
– This process is repeated for NI iterations, and different Wolf configurations are generated in each set of Iterations.
Due to these optimizations, the model can improve Energy Efficiency Ratio, Cost Savings Percentage, Control Signal Smoothness Index, Weighted Performance Index, TS, and Robustness Index for different scenarios. These parameters are evaluated for different circuit conditions and compared with existing models in the next section of this text.
3.5 Discussion about fusion of the proposed models
Multiple control techniques, including PI, PID, and FLC, are utilized and integrated into the ensemble predictive control model proposed for solar PV MPPT deployments. Here is a detailed explanation of how these control strategies are employed and combined:
-
Combining the Control Techniques: The proposed ensemble predictive control model incorporates and combines the PI, PID, and FLC to reap the benefits of these control techniques. Each controller has a distinct function within the overall control strategy, allowing the system to adapt to various operating conditions and enhance performance. The control methods were combined via an efficient hybrid control scheme, where the PI or PID controller functions as the principal controller for normal operating conditions, while the Fuzzy Logic controller handles specific scenarios or non-linearity. The transition between controllers may be governed by predefined conditions or imprecise rules that evaluate the state or performance criteria of the system.
By integrating these control techniques in the ensemble predictive control model, the proposed method can capitalize on the advantages of each technique to improve the performance of the PV system. The use of PI, PID, and FLC enables the system to manage various operating conditions, enhance tracking accuracy, and reduce the impact of uncertainties and non-linearity, resulting in more efficient and reliable solar PV MPPT deployments.
3.6 Need of VARMA, GRU, and LSTM
The inclusion of the predictive control features through the use of VARMA-GRU and LSTM models in the proposed ensemble predictive control model for solar PV MPPT deployments is essential for the reasons listed below:
Solar power generation is influenced by a number of variables, including weather conditions, solar irradiance, and demand variations. Traditional control models frequently function in a reactive manner, adjusting based on current measurements or sensor feedback. In contrast, the predictive control function provided by VARMA-GRU and LSTM models enables proactive decision-making. These models are capable of analyzing historical data, identifying patterns, and predicting future trends in power generation. Using these predictions, the control model is able to proactively optimize power generation and load management, resulting in enhanced system performance and efficiency.
3.7 Experimental setup
-
Simulation Environment: The experiments in this work were conducted using MATLAB/Simulation, a widely used simulation environment for system-level modeling and simulation.
-
SEPIC and Controller Simulation: The SEPIC converter and the ensemble predictive control model were simulated in MATLAB/Simulation. The SEPIC converter’s behavior was modeled using circuit equations and control algorithms implemented within Simulation blocks.
-
Converter Parameters: The specific parameters of the SEPIC converter used in the simulations were as follows:
-
Inductor values: L1 = 100 μH, L2 = 200 μH
-
Capacitor values: C1 = 100 μF, C2 = 220 μF
-
Switching frequency: 50 kHz
-
Duty cycle range: 0.2–0.8
-
-
Ideal Components and Control Laws: In this study, ideal components and control laws were considered to focus on the evaluation of the proposed control scheme’s performance. Non-idealistic, such as component losses and control system imperfections, were not taken into account.
-
PV Model and Solar Data: The simulations utilized the single-diode PV model, a widely used model for simulating PV panel behavior. The model includes parameters such as the short-circuit current (Isc), open-circuit voltage (Voc), diode ideality factor (n), and series and shunt resistances.
Solar data from a particular location were used to represent the solar irradiance and environmental conditions. For example, a solar dataset from the National Renewable Energy Laboratory (NREL) for a specific location could be utilized. Values for different components,
-
Inductor values: L1 = 100 μH, L2 = 200 μH.
-
Capacitor values: C1 = 100 μF, C2 = 220 μF.
-
Switching frequency: 50 kHz.
-
Duty cycle range: 0.2–0.8.
-
Short-circuit current (Isc): 6 A.
-
Open-circuit voltage (Voc): 25 V.
-
Diode ideality factor (n): 1.2.
-
Series resistance: 0.1 Ω.
-
Shunt resistance: 10 Ω.
Based on these values different simulation experiments were conducted, and their results are analyzed in the next section of this text.
4 Result in analysis and comparison
The proposed model uses a variety of control mechanisms, such as PID, MPPT, PI, and fuzzy controllers, to control solar PV systems selectively. The optimal parameters and configurations for each control device are found using the proposed bio-inspired optimization technique, resulting in a more thorough and effective method of controlling these devices for various scenarios. Our model includes a predictive control operation that uses a VARMA-GRU with an LSTM model, which can precisely forecast the solar system’s future power generation scenarios. This feature can improve the system’s overall performance for various use cases and enable more effective energy management under different use cases. This model was simulated for different conditions, and values for the Energy Efficiency Ratio, Cost Savings Percentage, Control Signal Smoothness Index, Weighted Performance Index, TS, and Robustness Index were estimated during these simulations. These simulation conditions are described as follows.
It can be observed that the proposed model is able to hold on to maximum power levels as observed in Figure 6, which makes it useful for high-performance applications. This is possible due to the use of high efficiency MPPT selection and control circuits, thereby improving the circuit’s response to varying radiation levels.
 |
Fig. 6 Power characteristics of the proposed model. |
It can be observed that the proposed model is able to maintain maximum power levels for different duty cycles as observed from Figure 7, which makes it useful for high-performance applications. This is possible due to the use of the high efficiency VARMA process, which improves the circuit’s response to varying radiation levels.
 |
Fig. 7 Power characteristics for different duty cycles of the proposed model. |
Due to dynamic changes in duty cycles, the voltage and current levels across the switch are maintained under dynamic load changes. This makes the model highly effective for real-time scenarios observed from Figure 8.
 |
Fig. 8 Current and voltage levels due to varying duty cycles. |
-
Solar Deployment Configuration:
-
Total number of solar panels: 3.
-
Solar panel capacity: 350 watts each.
-
-
Environmental Data:
-
Solar irradiance: Hourly data for a specific location (e.g., measured or simulated values).
-
Ambient temperature: Hourly data for the same location.
-
-
Control Parameters:
-
Prediction horizon: 24 h (divided into multiple time steps).
-
Control horizon: 6 h (number of time steps for which control actions are determined).
-
Control intervals: 1 h (time intervals at which control actions are updated).
-
Ensemble size: 5 (number of individual predictive control models in the ensemble).
-
-
Optimization Algorithm:
-
GWO.
-
Objective functions: Maximize energy generation, minimize cost, and maintain system stability.
-
-
Simulation Time:
-
Total simulation time: 7 days (168 h).
-
Time step size: 1 h.
-
-
Performance evaluation metrics:
-
Energy Efficiency Ratio (EER).
-
Cost Savings Percentage (CSP).
-
Control Signal Smoothness Index (CSSI).
-
Weighted Performance Index (WPI).
-
Settling Time (TS).
-
Robustness Index (RI).
-
-
Comparison Models:
Based on these conditions, the results were measured for STC (standard Temperature Conditions) and compared with those of the existing models. A sample of these simulation conditions (SCs) mentioned radiation in w/m2 and Temperature in °C, and various parametric evaluation metrics such as Energy Efficiency Ratio, Cost Savings Percentage, Control Signal Smoothness Index,Weighted Performance Index, Settling Time (in seconds), and Robustness Index observed in Table 1.
Simulation conditions (SCS) and parametric evaluations as per model.
Based on this analysis and Figure 9, it can be observed that the proposed model can improve the energy efficiency by 3–8% when compared with existing models under different simulation conditions. This is possible because on low-complexity feature extraction and optimization models improve the energy performance under different simulation conditions.
 |
Fig. 9 Energy Efficiency Ratio (EER) for different simulation conditions. |
Based on this analysis and Figure 10, it can be observed that the proposed model can improve the cost-saving percentage by 4.0–8.5% when compared with existing models under different simulation conditions. This is possible due to the use of GWO for tuning and VARMA for predictive analysis, which assists in improving the cost savings even under different simulation conditions.
 |
Fig. 10 Cost Savings Percentage (CSP) for different simulation conditions. |
Based on this analysis and Figure 11, it can be observed that the proposed model can optimize the CSSI levels by 8.3–10.4% when compared with existing models under different simulation conditions. This is possible due to the use of multiple control models for fine-tuning system outputs, which assist in smoothing the scontrol signal outputs even under different simulation conditions.
 |
Fig. 11 Control Signal Smoothness Index (CSSI) for different simulation conditions. |
Based on this analysis and Figure 12, it can be observed that the proposed model can optimize the WPI levels by 4–18% when compared with existing models under different simulation conditions. This is possible due to the use of multiple control models with VARMA for fine-tuning system outputs, which assist in smoothing control signal outputs and enhancing efficiency levels even under different simulation conditions.
 |
Fig. 12 Weighted Performance Index (WPI) for different simulation conditions. |
Based on this analysis and Figure 13, it can be observed that the proposed model can reduce the delay needed for the output to settle by 4–15% when compared with existing models under different simulation conditions. This is possible due to using VARMA with LSTM and GRU for fine-tuning system outputs, which assist in faster-settling output levels even under different simulation conditions.
 |
Fig. 13 Settling Time (Ts) for different simulation conditions. |
Based on this analysis and Figure 14, it can be observed that the proposed model can improve the robustness index by 3–8% when compared with existing models under different simulation conditions. This is possible due to the use of GWO Optimizations for multiple control units and use of VARMA with LSTM and GRU for fine-tuning system outputs, which assist in faster settling of output levels even under different simulation conditions. Due to these optimizations, the proposed model can be deployed in various real-time scenarios.
 |
Fig. 14 Robustness index for different simulation conditions. |
5 Conclusion
In this paper, using two bio-inspired optimizations, the author proposed an ensemble predictive control model for solar deployments. The findings show that model performs better than the existing models in terms of energy efficiency improving by 3–8%, cost savings improve by 4–8.5%, optimizing control signal smoothness by 8.3–10.4%, performance index by 4–18%, settling time by 4–15%, and robustness improve by 3–8% under various simulation conditions. Low-complexity feature extraction methods, optimization models like the GWO, and VARMA models for predictive analysis are combined to produce these improvements.
-
The necessity for cost-effective solar energy solutions drives this endeavor. As solar deployment grows, advanced control systems that maximize energy output, decrease costs, and ensure system stability are required. We present an ensemble predictive control model that improves solar resource used in different sectors.
-
This research affects several disciplines. Solar installations’ environmental effect and sustainability are reduced by our model’s energy efficiency. Energy generation optimization maximizes solar resource usage and reduces dependence on conventional energy. Second, our model’s cost reductions make solar installations more economically viable for people and enterprises. This may accelerate renewable energy adoption.
-
The proposed ensemble predictive control approach offers a broad variety of applications. It may be utilized in utility-scale solar farms, industrial complexes, commercial buildings, and residential solar systems. By improving energy efficiency, cost savings, and resilience, our model helps stakeholders make informed solar system design, operation, and optimization choices.
6 Future work
The proposed ensemble predictive control model for solar deployments will be further improved, validated, and expanded in this paper’s future work. Exciting new opportunities for research and practical applications in the field of solar energy optimization are made possible by the integration of advanced machine learning techniques, hybrid energy systems, energy storage optimization, adaptive control strategies, demand-side management, smart grid technologies, cost-benefit analysis, scalability, and integration with building energy management systems.
Conflict of interest
The authors declare that there is no conflict of interest.
References
- Pérez Guzmán R.E., Rivera M., Wheeler P.W., Mirzaeva G., Espinosa E.E., Rohten J.A. (2022) Microgrid power sharing framework for software defined networking and cybersecurity analysis, IEEE Access 10, 111389–111405. https://doi.org/10.1109/ACCESS.2022.3215434. [CrossRef] [Google Scholar]
- Li Y., Diao F., Zhao Y. (2021) Simplified two-stage model predictive control for a hybrid multilevel converter with floating h-bridge, IEEE Trans. Power Electron. 36, 4, 4839–4850. https://doi.org/10.1109/TPEL.2020.3018956. [CrossRef] [Google Scholar]
- Alhosaini W., Diao F., Mahmud M.H., Wu Y., Zhao Y. (2021) A virtual space vector-based model predictive control for inherent dc-link voltage balancing of three-level t-type converters, IEEE J. Emerg. Sel. Top. Power Electron. 9, 2, 1751–1764. https://doi.org/10.1109/JESTPE.2020.3002192. [CrossRef] [Google Scholar]
- Silva J.J., Espinoza J.R., Rohten J.A., Pulido E.S., Villarroel F.A., Torres M.A., Reyes M.A. (2020) MPC algorithm with reduced computational burden and fixed switching spectrum for a multilevel inverter in a photovoltaic system, IEEE Access 8, 77405–77414. https://doi.org/10.1109/ACCESS.2020.2988627. [CrossRef] [Google Scholar]
- Khan K., Shukla S., Singh B. (2020) Improved performance design realization of a fractional kilowatt induction motor with predictive current control for water pumping, IEEE Trans. Ind. Appl. 56, 4, 4575–4587. https://doi.org/10.1109/TIA.2020.2968014. [Google Scholar]
- Dutta A., Ganguly S., Kumar C. (2022) MPC-based coordinated voltage control in active distribution networks incorporating CVR and DR, IEEE Trans. Ind. Appl. 58, 4, 4309–4318. https://doi.org/10.1109/TIA.2022.3163108. [CrossRef] [Google Scholar]
- Li Y., Diao F., Zhao Y. (2022) A phase-disposition pwm-enabled model predictive control for a nine-level inner-interleaved hybrid multilevel converter, IEEE J. Emerg. Sel. Top. Power Electron. 10, 6, 6784–6796. https://doi.org/10.1109/JESTPE.2021.3130056. [CrossRef] [MathSciNet] [Google Scholar]
- Li Y., Diao F., Zhao Y., Mantooth H.A. (2022) A hybrid model predictive control for a seven-level hybrid multilevel converter with independent low-frequency and high-frequency stages, IEEE Trans. Power Electron. 37, 5, 5256–5271. https://doi.org/10.1109/TPEL.2021.3132629. [CrossRef] [MathSciNet] [Google Scholar]
- Tarnate W.R.D., Ponci F., Monti A. (2022) Uncertainty-aware model predictive control for residential buildings participating in intraday markets, IEEE Access 10, 7834–7851. https://doi.org/10.1109/ACCESS.2022.3140598. [CrossRef] [Google Scholar]
- Ahmad S.S., Al-Ismail F.S., Almehizia A.A., Khalid M. (2020) Model predictive control approach for optimal power dispatch and duck curve handling under high photovoltaic power penetration, IEEE Access 8, 186840–186850. https://doi.org/10.1109/ACCESS.2020.3030100. [CrossRef] [Google Scholar]
- Zhou L., Preindl M. (2023) Hierarchical software-defined control architecture with mpc-based power module to interface renewable sources and motor drives, IEEE Trans. Sustain. Energy 14, 1, 83–96. https://doi.org/10.1109/TSTE.2022.3202957. [CrossRef] [Google Scholar]
- Qiu Y., Lin J., Liu F., Song Y., Chen G., Ding L. (2020) Stochastic online generation control of cascaded run-of-the-river hydropower for mitigating solar power volatility, IEEE Trans. Power. Syst. 35, 6, 4709–4722. https://doi.org/10.1109/TPWRS.2020.2991229. [CrossRef] [Google Scholar]
- Poonahela I., Bayhan S., Abu-Rub H., Begovic M.M., Shadmand M.B. (2021) An effective finite control set-model predictive control method for grid integrated solar PV, IEEE Access 9, 144481–144492. https://doi.org/10.1109/ACCESS.2021.3122325. [CrossRef] [Google Scholar]
- Tang L., Xu W., Wang X., Dong D., Xiao X., Zhang Y. (2021) Weighting factors optimization of model predictive control based on fuzzy thrust constraints for linear induction machine, IEEE Trans. Appl. Supercond. 31, 8, 1–5. https://doi.org/10.1109/TASC.2021.3103704. [CrossRef] [Google Scholar]
- Villarroel F.A., Espinoza J.R., Pérez M.A., Baier C.R., Rohten J.A., Ramírez R.O., Pulido E.S., Silva J.J. (2022) A predictive shortest-horizon voltage control algorithm for non-minimum phase three-phase rectifiers, IEEE Access 10, 107598–107615. https://doi.org/10.1109/ACCESS.2022.3212731. [CrossRef] [Google Scholar]
- Tuan H.D., Nasir A.A., Savkin A.V., Poor H.V., Dutkiewicz E. (2021) MPC-based uav navigation for simultaneous solar-energy harvesting and two-way communications, IEEE J. Sel. Areas Commun. 39, 11, 3459–3474. https://doi.org/10.1109/JSAC.2021.3088633. [CrossRef] [Google Scholar]
- Abdel-Rahim O., Wang H. (2020) A new high gain DC-DC converter with model-predictive-control based MPPT technique for photovoltaic systems, CPSS Trans. Power. Electron. Appl. 5, 2, 191–200. https://doi.org/10.24295/CPSSTPEA.2020.00016. [CrossRef] [Google Scholar]
- Mahfuz-Ur-Rahman A.M., Islam M.R., Muttaqi K.M., Sutanto D. (2020) Model predictive control for a new magnetic linked multilevel inverter to integrate solar photovoltaic systems with the power grids, IEEE Trans. Ind. Appl. 56, 6, 7145–7155. https://doi.org/10.1109/TIA.2020.3024352. [CrossRef] [Google Scholar]
- Fonseca A.D.N., Gómez J.S., Llanos J., Rute E., Sáez D., Sumner M. (2021) Distributed predictive control strategy for frequency restoration of microgrids considering optimal dispatch, IEEE Trans. Smart Grid 12, 4, 2748–2759. https://doi.org/10.1109/TSG.2021.3053092. [CrossRef] [Google Scholar]
- Elmorshedy M.F., Habib H.U.R., Ali M.M., Sathik M.J., Almakhles D.J. (2022) Improved performance of hybrid pv and wind generating system connected to the grid using finite-set model predictive control, IEEE Access 10, 110344–110361. https://doi.org/10.1109/ACCESS.2022.3214996. [CrossRef] [Google Scholar]
- Vanti S., Bana P.R., D’Arco S., Amin M. (2022) Single-stage grid-connected pv system with finite control set model predictive control and an improved maximum power point tracking, IEEE Trans. Sustain. Energy 13, 2, 791–802. https://doi.org/10.1109/TSTE.2021.3132057. [CrossRef] [Google Scholar]
- Cuzmar R.H., Pereda J., Aguilera R.P. (2021) Phase-shifted model predictive control to achieve power balance of chb converters for large-scale photovoltaic integration, IEEE Trans. Ind. Electron. 68, 10, 9619–9629. https://doi.org/10.1109/TIE.2020.3026299. [CrossRef] [Google Scholar]
- Zhao B., Zhao Z., Huang M., Zhang X., Li Y., Wang R. (2021) Model predictive control of solar pv-powered ice-storage air-conditioning system considering forecast uncertainties, IEEE Trans. Sustain. Energy 12, 3, 1672–1683. https://doi.org/10.1109/TSTE.2021.3061776. [CrossRef] [Google Scholar]
- Bai Y., Hu S., Yang Z., Zhu Z., Zhang Y. (2022) Model predictive control for four-switch buck–boost converter based on tuning-free cost function with smooth mode transition, IEEE J. Emerg. Sel. Top. Power Electron. 10, 6, 6607–6618. https://doi.org/10.1109/JESTPE.2021.3133837. [CrossRef] [Google Scholar]
- Yin J., Leon J.I., Perez M.A., Franquelo L.G., Marquez A., Li B., Vazquez S. (2021) Variable rounding level control method for modular multilevel converters, IEEE Trans. Power Electron. 36, 4, 4791–4801. https://doi.org/10.1109/TPEL.2020.3020941. [CrossRef] [Google Scholar]
- Leomanni M., Bianchini G., Garulli A., Quartullo R. (2022) Sum-of-norms periodic model predictive control for space rendezvous, IEEE Trans. Control Syst. Technol. 30, 3, 1311–1318. https://doi.org/10.1109/TCST.2021.3095390. [CrossRef] [Google Scholar]
- Laib A., Krama A., Sahli A., Kihal A., Abu-Rub H. (2022) Reconfigurable model predictive control for grid connected PV systems using thirteen-level packed e-cell inverter, IEEE Access 10, 102210–102222. https://doi.org/10.1109/ACCESS.2022.3208106. [CrossRef] [Google Scholar]
- Yin J., Leon J.I., Perez M.A., Franquelo L.G., Marquez A., Vazquez S. (2021) Model predictive control of modular multilevel converters using quadratic programming, IEEE Trans. Power Electron. 36, 6, 7012–7025. https://doi.org/10.1109/TPEL.2020.3034294. [CrossRef] [Google Scholar]
- Groß A., Wille-Haussmann B., Wittwer C., Achzet B., Diehl M. (2023) Stochastic nonlinear model predictive control for a switched photovoltaic battery system, IEEE Trans. Control Syst. Technol. 31, 2, 969–976. https://doi.org/10.1109/TCST.2022.3208822. [CrossRef] [MathSciNet] [Google Scholar]
- Su H.-Y., Liu T.-Y., Hong H.-H. (2020) Adaptive residual compensation ensemble models for improving solar energy generation forecasting, IEEE Trans. Sustain. Energy 11, 2, 1103–1105. https://doi.org/10.1109/TSTE.2019.2931154. [CrossRef] [MathSciNet] [Google Scholar]
- Maqueda E., Toledo S., Caballero D., Gavilan F., Rodas J., Ayala M., Delorme L., Gregor R., Rivera M. (2021) Speed control of a six-phase im fed by a multi-modular matrix converter using an inner PTC with reduced computational burden, IEEE Access 9, 160035–160047. https://doi.org/10.1109/ACCESS.2021.3130786. [CrossRef] [Google Scholar]
- Ingalalli A., Kamalasadan S. (2023) Decentralized state estimation-based optimal integral model predictive control of voltage and frequency in the distribution system microgrids, IEEE Trans. Smart Grid 14, 3, 1790–1803. https://doi.org/10.1109/TSG.2022.3220714. [CrossRef] [Google Scholar]
- Li Y., Diao F., Zhao Y. (2021) A generic two-vector model predictive control for hybrid multilevel converters, IEEE J. Emerg. Sel. Top. Power Electron. 9, 5, 6008–6018. https://doi.org/10.1109/JESTPE.2021.3079927. [CrossRef] [Google Scholar]
- Singh S., Veda S., Singh S.P., Jain R., Baggu M. (2021) Event-driven predictive approach for real-time Volt/VAR control with CVR in solar PV rich active distribution network, IEEE Trans. Power. Syst. 36, 5, 3849–3864. https://doi.org/10.1109/TPWRS.2021.3057656. [CrossRef] [Google Scholar]
- Rehman S., Habib H.U.R., Wang S., Büker M.S., Alhems L.M., Al Garni H.Z. (2020) Optimal design and model predictive control of standalone HRES: a real case study for residential demand side management, IEEE Access 8, 29767–29814. https://doi.org/10.1109/ACCESS.2020.2972302. [CrossRef] [Google Scholar]
- Lupangu C., Justo J.J., Bansal R.C. (2020) Model predictive for reactive power scheduling control strategy for PV-battery hybrid system in competitive energy market, IEEE Syst. J. 14, 3, 4071–4078. https://doi.org/10.1109/JSYST.2020.2968926. [CrossRef] [Google Scholar]
- Bao P., Zhang W., Zhang Y. (2021) Secondary frequency control considering optimized power support from virtual power plant containing aluminum smelter loads through VSC-HVDC link, J. Mod. Power Syst. Clean Energy 11, 1, 355–367. https://doi.org/10.35833/MPCE.2021.000072. [Google Scholar]
- Yaru Z., Qinglong L., Ming X., Yunfeng D. (2021) An integrated simulation system for operating solar sail spacecraft, J. Syst. Eng. Electron. 32, 5, 1200–1211. https://doi.org/10.23919/JSEE.2021.000102. [CrossRef] [Google Scholar]
- Ouammi A. (2021) Peak loads shaving in a team of cooperating smart buildings powered solar PV-based microgrids, IEEE Access 9, 24629–24636. https://doi.org/10.1109/ACCESS.2021.3057458. [CrossRef] [Google Scholar]
- Kang J., Zhu Z.H. (2023) Passivity-based model predictive control for tethered despin of massive space objects by small space tug, IEEE Trans. Aerosp. Electron. Syst. 59, 2, 1239–1248. https://doi.org/10.1109/TAES.2022.3197097. [Google Scholar]
- Chen W.-H., You F. (2022) Semiclosed greenhouse climate control under uncertainty via machine learning and data-driven robust model predictive control, IEEE Trans. Control Syst. Technol. 30, 3, 1186–1197. https://doi.org/10.1109/TCST.2021.3094999. [CrossRef] [Google Scholar]
- Heydari R., Young H., Flores-Bahamonde F., Vaez-Zadeh S., González-Castaño C., Sabzevari S., Rodríguez J. (2022) Model-free predictive control of grid-forming inverters with LCL filters, IEEE Trans. Power Electron. 37, 8, 9200–9211. https://doi.org/10.1109/TPEL.2022.3159730. [CrossRef] [Google Scholar]
- Bairami S., Salimi M., Mirabbasi D. (2023) A novel method for maximum power point tracking of the grid-connected three-phase solar systems based on the PV current prediction, Chin. J. Electron. 32, 2, 353–364. https://doi.org/10.23919/cje.2021.00.218. [CrossRef] [Google Scholar]
- Mahdavi S., Panamtash H., Dimitrovski A., Zhou Q. (2021) Predictive coordinated and cooperative voltage control for systems with high penetration of PV, IEEE Trans. Ind. Appl. 57, 3, 2212–2222. https://doi.org/10.1109/TIA.2021.3064910. [CrossRef] [Google Scholar]
- Sun Q., Li Y., Ma D., Zhang Y., Qin D. (2022) Model predictive direct power control of three-port solid-state transformer for hybrid AC/DC zonal microgrid applications, IEEE Trans. Power Deliv. 37, 1, 528–538. https://doi.org/10.1109/TPWRD.2021.3064418. [CrossRef] [Google Scholar]
- Hole S.R., Goswami A.D. (2022) Quantitative analysis of DC–DC converter models: a statistical perspective based on solar photovoltaic power storage, Energy Harvest Syst. 9, 1, 113–121. https://doi.org/10.1515/ehs-2021-0027. [CrossRef] [Google Scholar]
- Liang J., Li T., Zhang R., Dong L. (2023) Reactive voltage control strategy of distribution network considering the reliability of photovoltaic power supply, Sci. Technol. Energy Transit. 78, 34. https://doi.org/10.2516/stet/2023032. [CrossRef] [Google Scholar]
- Muller D.C., Selvanathan S.P., Cuce E., Kumarasamy S. (2023) Hybrid solar, wind, and energy storage system for a sustainable campus: a simulation study, Sci. Technol. Energy Transit. 78, 13. https://doi.org/10.2516/stet/2023008. [CrossRef] [Google Scholar]
- Hole S.R., Goswami A.D. (2023) Design of an efficient MPPT optimization model via accurate shadow detection for solar photovoltaic, Energy Harvest Syst. 10, 2, 377–383. https://doi.org/10.1515/ehs-2022-0151. [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Design of the proposed model for optimization of Solar PV Deployments. |
| In the text | |
 |
Fig. 2 Conversion of power, control, and load parameters into multi-modal feature sets. |
| In the text | |
 |
Fig. 3 PID controller work flow chart. |
| In the text | |
 |
Fig. 4 PI controller work flow chart. |
| In the text | |
 |
Fig. 5 The SEPIC converter used for simulation operations. |
| In the text | |
 |
Fig. 6 Power characteristics of the proposed model. |
| In the text | |
 |
Fig. 7 Power characteristics for different duty cycles of the proposed model. |
| In the text | |
 |
Fig. 8 Current and voltage levels due to varying duty cycles. |
| In the text | |
 |
Fig. 9 Energy Efficiency Ratio (EER) for different simulation conditions. |
| In the text | |
 |
Fig. 10 Cost Savings Percentage (CSP) for different simulation conditions. |
| In the text | |
 |
Fig. 11 Control Signal Smoothness Index (CSSI) for different simulation conditions. |
| In the text | |
 |
Fig. 12 Weighted Performance Index (WPI) for different simulation conditions. |
| In the text | |
 |
Fig. 13 Settling Time (Ts) for different simulation conditions. |
| In the text | |
 |
Fig. 14 Robustness index for different simulation conditions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.