| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 6 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.2516/stet/2023044 | |
| Published online | 16 January 2024 | |
Regular Article
Optimizing PV integration: Addressing energy fluctuations through BIPV and rooftop PV synergy
National Institute of Technology Patna (NIT Patna), Bihar 800005, India
* Corresponding author: saketsaur@gmail.com
Received:
29
July
2023
Accepted:
20
December
2023
The widespread availability and affordability of photovoltaic (PV) systems are driving the future of demand-side generation towards end-user-based PV plants. Building-integrated PV systems offer an additional source of electrical energy, but their power output depends on external factors like solar insolation, weather conditions, geographical location, and earth’s rotation, causing non-constant energy generation, even in ideal weather conditions. In grid-connected systems, this variability leads to fluctuations in grid demand. Both BIVP and rooftop PV systems are photovoltaic-based, but their installation differences result in distinct energy generation characteristics. To address this, we propose an innovative approach to optimally integrate BIPV and rooftop PV systems by leveraging their contradictory energy generation nature. By employing mathematical and evolutionary algorithms to design an optimal system and develop a multi-objective optimization model, we address practical design issues. The outcome of these single and multi-objective systems helps minimize fluctuations in grid dependency throughout the year. The proposed system is validated on the IEEE-33 bus radial distribution network using the B&R X20CP1586 PLC, confirming its effectiveness in ensuring a stable and reliable grid performance while mitigating energy fluctuation impacts.
Key words: PV / BIPV / Roof-top / Optimization / Genetic algorithm / Renewable-energy
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the years to come, there will be a rise in energy demand as a result of urbanisation and major growth in the building infrastructure of both commercial and residential buildings. The percentage of people living in cities is expected to reach 65 per cent by the year 2050 [1–3], which would result in a 52 per cent rise in the demand for energy worldwide between 2018 and 2040. Already, 30–40 per cent of the world’s energy consumption is accounted for by buildings [4], and this proportion is growing at a pace of 2.7 per cent annually [5]. The rising demand for energy poses a threat to energy security, puts strain on the system, and increases GHG emissions, which in turn risks global warming [6, 7]. As the price of photovoltaic cells falls [8, 9], the installation of solar panels on rooftops is becoming increasingly frequent. However, the amount of space required for installation is greater, and this space is typically in short supply in contemporary cities. By installing BIPV modules on the exterior of buildings, the disadvantage of putting solar panels on rooftops can be significantly mitigated [10].
PV solar panels installed on the building’s façade are capable of combining the generation of electricity with other activities [11]. Solar photovoltaic (PV) applications in urban areas are advancing at a rapid rate, which has led an increasing number of nations to prioritise the incorporation of PV into the building industry [12]. For instance, the solar photovoltaic (PV) system can balance peak electricity output from coal and gas, saving traditional energy [13]. PV systems with power-saving capabilities are essential in today’s buildings [14]. PV is now more expensive than power from the grid by a factor of five; nonetheless, it is anticipated that PV will play a significant role in the generation of mainstream electricity during the next century [15].
The use of photovoltaic, or PV, technology to collect solar energy is an attractive and effective method [16]. In the future, applications of solar photovoltaics will place an emphasis on efficiency, building-integrated photovoltaics (BIPV), cost reduction, and the development of a storage system. Using the BIPV product, we may convert our building into an energy generator.
For optimal performance, the product and the BIPV technology must be integrated together [17]. BIPV devices have multiple applications, including usage on roofs, facades, and skylights [17]. Additionally, the BIPV product offers protection against the elements, thermal insulation, and a reduction in noise.
A normal photovoltaic (PV) system does not offer the same benefits that a building-integrated photovoltaic (BIPV) system does in terms of making the most of the building’s structure. This is one of the primary advantages of a BIPV system.
When applied to a high-rise building, the installation of a photovoltaic (PV) system that is built on the building’s facade will be beneficial since it will solve the issue of dealing with a limited quantity of roof space.
The global market for BIPV products is massive, and there is a significant opportunity for expansion in this industry. In recent years, there has been an increase in the total expansion of BIPV, which currently stands at roughly 2000 MW of installations that have been completed [18].
Intermittence of PV generation is a major issue for its future [19, 20]. Additional installation of the BIPV system will further increase the potential generation capacity, but it will also introduce more issues with the fluctuation in actual energy generation. Due to intermittency, the power grid is restricting the maximum injection for its stability [21, 22]. In some locations, the grid operators restrict the end user from injecting any power into the main grid. If this trend is going to continues, even if we are able to install large PV plants, will not able to harvest the potential of its generation capacity.
To resolve this issue of the fluctuations in the generation capacity, in this paper, the authors proposed a novel approach to utilize the roof-top and BIPV systems’ per-day energy characteristics. It is observed by the authors that in a range of geographical locations, the per-day energy production profile of facade-based BIPV systems and rooftop PV is contradictory. During the peak energy season of the rooftop, the BIPVs are generating a minimum energy and vice-versa.
The highlights of this research are: (1) Mathematical model development for BIPV and rooftop integration. (2) Optimal PV plant sizing for a flat energy generation profile. (3) Optimal sizing via mathematical and evolutionary optimization. (4) Multi-objective optimization for a more practical design approach to provide multiple options to power system designers for project implementation. (5) Validation of the proposed mathematical model with real field data, which confirms the applicability of the proposed approach.
The organization of this paper is as follows: the following section starts with mathematical modelling of an earth’s geometry-dependent generic PV panel’s electrical output. A solar irradiation model with a PV panel output model has been developed. In Section 3, problem formulation is defined with theoretical as well as mathematical model-based approaches. In the current section, the single-objective and multi-objective optimization fitness functions are defined. The following section gives a description of the test system which is considered in the research paper. The result and discussion of both the objective functions for different test systems are given in Section 5. Finally, the conclusion section ends with the concluding comments and future prospects of this research work.
2 Mathematical model
2.1 PV panel power generation
In a PV system, the solar panels are the fundamental building block for the electricity generation system. The solar panels produce electricity when a photon strikes the surface of the panels. The kinetic energy of photons is converted into the flow of electrons in the PV cells. The PV cells are arranged into mesh form for converting this small voltage and current level to the required level.
To mathematically model the PV panels’ output, we need to model the PV panel input dependencies. The input to the PV panel is solar irradiation, which is a time-dependent and environment-dependent parameter. The PV panel output is related to the solar irradiance incident on it at any moment of time. The solar irradiance model requires information regarding the earth’s relative position with respect to the sun, the location where the PV panels are installed, the inclination of the PV panels, etc.
2.1.1 Global normal irradiance
For formulating the irradiance model [23, 24] on the surface of the earth, first we need to model the solar irradiance above the earth’s atmosphere, which is called global normal irradiance (GNI). The earth revolves around the sun in an elliptical orbit. Due to the earth’s motion, the amount of sunlight received on the earth varies with the day of the year. This variation of the irradiance can be characterised by equation (1) and Figure 2.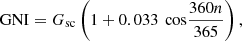 (1)
where,
(1)
where,
GNI = extra terrestrial global normal radiation (kW/m2).
G sc = solar constant (1.367 kW/m2).
n = day of the year (1–365 starting from Jan 1).
 |
Figure 1 Roof top solar panel. |
 |
Figure 2 Global extra terrestrial irradiance. |
 |
Figure 3 BIPV facade based PV system. |
2.1.2 Global Horizontal Irradiance (GHI)
The irradiation that is provided by the sun will vary from one region of the world to another. Because the earth is spherical, the component of the sun’s irradiance that hits the surface of the solar panel is the horizontal component of the GNI. This component is known as the Global Horizontal Irradiance (GHI) [25], and it may be defined as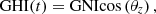 (2)where,
(2)where,
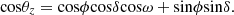
θ z = solar Zenith angle.
ϕ = latitude.
δ = sun declination angle.
ω = hour angle,
t = time.
In this paper, the mathematical model is done in a discrete time domain thus the continuous time model of equation (2) needs to be converted into a discrete time interval model. The time discretisation is considered as 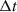 . The conversion of equation (2) is taking the average value of the GHI (i.e. AGHI) over the time interval (
. The conversion of equation (2) is taking the average value of the GHI (i.e. AGHI) over the time interval (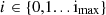 ), which can be calculated by equation (3)
), which can be calculated by equation (3)
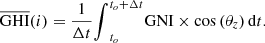 (3)
(3)
2.2 Solar irradiation on the surface of earth
The Hay–Davies–Klucher–Reindl (HDKR) [26, 27] model calculates the global irradiation incident on a PV array according to the following equation![$$ {\bar{G}}_T=\left({\bar{G}}_b+{\bar{G}}_d{A}_i\right){R}_b+{\bar{G}}_d\left(1-{A}_i\right)\frac{1+\mathrm{cos}\left(\beta \right)}{2}\left[1+f{\mathrm{sin}}^3\frac{\beta }{2}\right]+\widehat{G}{\rho }_g\frac{1-\mathrm{cos}\beta }{2}. $$](/articles/stet/full_html/2024/01/stet20230135/stet20230135-eq7.gif) (4)
(4)
The degree to which the atmosphere is free of cloudiness is indicated by a number known as the clearness index. It refers to the amount of solar energy that is able to penetrate the earth’s atmosphere and reach its surface. It is a number with no dimensions that range from 0 to 1 and is defined as the ratio of the radiation from the surface to the extraterrestrial radiation value. When there is little to no cloud cover, the clearness index will register a high number, and when there is a lot of cloud cover, it will register a low value. The beam radiation on the PV panel is a function of the global horizontal index and the clearness index (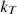 ) [28].
) [28].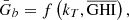 (5)where,
(5)where,
A i = anisotropy index.
ρ = the ground reflection, which is also called as albedo.
β = the slope of the surface.
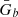 = beam radiation.
= beam radiation.
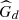 = diffused radiation (kW/m2) [29].
= diffused radiation (kW/m2) [29].
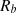 = ratio of beam radiation of the tilted surface to the beam radiation on the horizontal surface.
= ratio of beam radiation of the tilted surface to the beam radiation on the horizontal surface.
2.3 PV panel electrical power
The photovoltaic solar panel electrical output can be estimated by the following formula [30]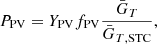 (6)where,
(6)where,
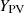 = the rated capacity of the PV array at standard test condition (kW).
= the rated capacity of the PV array at standard test condition (kW).
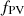 = PV derating factor (fraction).
= PV derating factor (fraction).
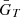 = solar irradiance incidence on the surface of earth.
= solar irradiance incidence on the surface of earth.
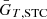 = incident radiation at standard test condition (1 kW/m2).
= incident radiation at standard test condition (1 kW/m2).
STC = standard test conditions.
3 Problem formulation
A building-integrated photovoltaic (BIPV) is basically a PV system integrated with the building structure. When compared with roof-top PV systems, the facade-based BIPVs are installed at a much steeper angle.
Since the BIPV model is the same as normal PV, all the mathematical models developed in Section 2 are applicable to BIPV modules. The facade-based BIPV system is installed on the outer wall of a building at an inclination that is able to vary from 80° to 90°. The PV power output model is the same as the rooftop system. The close similarities between these two systems only differ in solar irradiation level. The steep angle of the solar irradiation received by BIPV mainly constitutes diffused or reflected components of the sun’s irradiation on the surface of the earth. Further, the steep angle of the system makes it very difficult to direct sunlight.
Based upon the mathematical model developed in Section 2 equation (4) is used to simulate the variation of electrical energy production. The PV plant location is taken at 25.618201° north and 85.183081° east. Electrical energy production of a PV panel throughout the year varies. The per-day energy generation profile differs from with PV’s panel inclination angle. Figure 4 is a mathematical output of the PV production. The simulation results confirm the dramatic variation of per day energy production when the PV inclination angle is increased from 0° to 90°. From the plant’s perspective, the lower inclination angle corresponds to the rooftop system, and the higher and steep inclination angle can be considered as the BIPV system.
 |
Figure 4 Energy production at different inclination angle. |
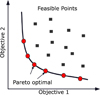 |
Figure 5 Pareto optimal curve in a multi-objective optimization. |
 |
Figure 6 The maximum number of PV that can be installed on roof-top and facade. |
The behaviour of the PV and BIPV systems is quite contradictory. This behaviour is only valid when both systems are located between 30° north and 30° south of the equator. From the figure, it can be concluded that the energy generation capability of the root-top system is not constant throughout the year. The amount of power that can be made changes depending on the angle of the PV panels and how the earth moves around the sun.
The energy output characteristics of BIPV and rooftop systems are opposite in nature. Based on this behaviour, the authors propose a novel approach to utilise the BIPV-based system to compensate for the loss in the generation capability of rooftop-based PV systems. Because the loss in the rooftop system can be compensated for by the addition of a facade-based PV system, An optimal sizing of the two types of PV systems, i.e., rooftop and BIPV, has a strong synergy between them and can be exploited during the project planning period.
3.1 Optimization model
The above-mentioned problem of finding the optimal size of PV and BIPV modules such that the energy production of the solar system installed in a home is least affected throughout the year can be modelled as an optimization problem. The power output of each rooftop (RT) and BIPV varies with the day-by-day scenario, so the energy output will vary. A single objective optimization to compensate for the PV output loss is modelled as the minimization of the peak-to-average ratio of the energy output of the total solar installed capacity.
In this paper, the authors have considered multiple test cases to validate the proposed application of the BIPV system. Case 1 is modelled as a single objective minimization problem of variation in energy production of RT and BIPV. This problem can be represented by the objective function defined in equation (7).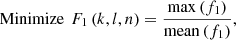 (7)
(7)
where,
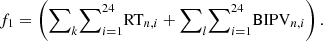
 = day in a year.
= day in a year.
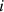 = hour in a day.
= hour in a day.
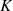 and
and 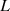 are the maximum number of RT and BIPV modules that can be installed.
are the maximum number of RT and BIPV modules that can be installed.
The primary goal of a PV installation is to provide the most power possible from the available infrastructure resources. The optimal value of equation (7) may not be necessary to the point of maximum PV plant size which leads to under-utilisation of building infrastructure. Thus, a second case study is considered to study these effects on the installation capacity. The maximum PV power output depends upon the maximization of installed capacity, which combines both the rooftop and BIPV installations. This problem of maximum PV output from the available resources can be modelled as the maximization problem, as given in equation (8).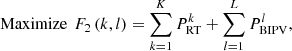 (8)
(8)
where,
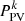 = maximum power output of kth installed rooftop panel.
= maximum power output of kth installed rooftop panel.
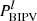 = maximum power output of lth installed BIPV panel.
= maximum power output of lth installed BIPV panel.
In a PV plant, it is generally observed that only one type and size of PV panels are used to avoid any compatibility issues. Mixing of different sizes of PV panels will lead to an imbalance in string voltage, which may lead to stress on the different PV strings if multiple strings are connected in parallel. If the ratings of all the PV panels are equal, then equation (8) can be rewritten as equation (9).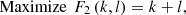 (9)
(9)
where,
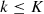 .
.
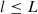 .
.
3.2 Optimization algorithm
In this paper, the optimization problem is of two types, which are single-objective and multi-objective optimization. The single objective problem is solved using mathematical non-linear programming and the single objective genetic algorithm. On the other hand, the multi-objective optimization is solved using the non-dominated genetic algorithm (NSGA-II).
3.2.1 Single objective optimization algorithm
Non-linear programming (NLP) is a method of solving an optimization problem when some constraints or objective functions are non-linear. (10)
(10)
The optimization of the objective function  in NLP entails calculating the extrema (maxima, minima, or stationary points) of over a set of unknown real variables
in NLP entails calculating the extrema (maxima, minima, or stationary points) of over a set of unknown real variables 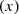 and is dependent on the satisfaction of a system of inequalities
and is dependent on the satisfaction of a system of inequalities 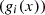 and equalities
and equalities 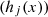 .
.
On the other hand, the genetic algorithm is a method for solving optimization problems that is based on natural selection, the process that causes biological evolution. This method can be used to solve optimization problems that have constraints as well as those that do not have constraints.
An existing population of individual problems is subjected to the genetic algorithm’s iterative editing process. At each stage of the process, the genetic algorithm chooses members of the existing population to serve as parents, and then employs those individuals to produce the offspring that will comprise the following/next generation.
A population “evolves” toward a problem that can be solved most effectively as time passes and new generations are born. We can use the genetic algorithm to solve a variety of optimization problems that are not well-suited for standard optimization algorithms. These problems include problems in which the objective function is discontinuous, non-differentiable, stochastic, or highly non-linear. These problems can all be solved by applying the genetic algorithm. The evolutionary algorithm can be used to solve problems that arise in mixed integer programming, which is a type of programming in which certain components are required to have integer values.
3.2.2 Multi-objective genetic algorithm
In multi-objective optimization problems, resolving competing objectives is one of the primary focuses. This means that while one objective improves, another must become less important. There is not one one answer that can be used everywhere; rather, there is a collection of answers. In addition to this, the problem is constrained by a number of different inequality and equality considerations. Furthermore, an upper and/or lower bound is linked with each variable, depending on the context. The term “feasible points” refers to a solution that satisfies all of the requirements placed on it as well as the limits placed on the variables involved. The non-dominated sorting genetic algorithm II (NSGA-II) program is an example of an evolutionary algorithm. The traditional direct and gradient-based methods have the following issues when working with non-linearities and complicated interactions; therefore, evolutionary algorithms were developed as a solution to these issues.
The initial solution that is selected has a direct bearing on whether or not the system will converge on the best possible solution. The vast majority of algorithms have a strong propensity to become mired in a solution that is less than ideal. The NSGA-II is an example of an evolutionary algorithm, and it possesses all three of the following characteristics:
It operates on the basis of an elitist principle, which states that the most successful members of a population should be given the opportunity to pass on their traits to subsequent generations. It does this by employing a mechanism for explicitly preserving diversity known as crowding distance, and it places an emphasis on solutions that are not dominated. The two different objectives are considered in this paper for multi-objective optimization. The fitness functions are; minimization of electrical energy variation equation (7) and maximum utilisation of PV installation area equation (9).
4 Test system
This research work is concentrated on the feasibility of PV system installation in urban buildings. Thus, considering the different sizes of buildings is very important to validate the proposed application. A developing country locality is mainly targeted where the house sizes vary from small to big. The different sizes of the houses will determine the rooftop area and the facade area for BIPV installation. In other words, the building structure and size will be the determining criterion of the PV system installation capabilities.
Therefore, ten types of test cases are considered, which are based on house sizes. The house’s size determines the maximum rooftop area as given Table 1, which will ultimately define the PV plant installation size. The floor area requirement for PV panels is taken from (needed citation). For different test cases, the maximum PV plant size is calculated, which also determines the number of PV panels that can be installed in any given test case.
Roof-top area.
The maximum number of PV panels will determine the variable bonds of the optimization model. The optimizer will search for the optimal solution that corresponds to the integer number of the PV panels that can be installed. Here, in this research work, each PV panel considered is rated as 330 Watts of mono-crystalline passivated emitter and rear cell (mono-perc) panels.
The optimization results are validated on the IEEE-33 bus system Figure 7. The PV system is installed in a radial distribution network node. The PV installation node is not considered fixed as given in the figure. In the test system, the PV installation point is optimally selected to improve the voltage profile and minimise the distribution network power loss.
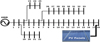 |
Figure 7 Modified IEEE-33 bus radial distribution network. |
The test setup is implemented as control hardware in loop (CHIL) on a PLC. In the current test system, the ABB-B&R X20CP1586 is used as controller hardware to implement in real time. To validate the results, the system needs to be run for the project’s lifetime. To accelerate this process, a time quantization of 1000 ms is considered 1 h in real time. Thus, the whole controller can emulate the project in accelerated mode.
5 Results and discussion
5.1 Mathematical model validation
The mathematical model to simulate the PV electrical output was developed in Section 2. To confirm the validity of the model, the simulated output is compared with the field data recorded. A 1 kW rooftop system Figure 8 installed at 25.618201° north and 85.183081° east. The system has mono-crystalline panels and a dedicated micro-inverter with an aggregated data logger. Monitoring data is securely stored locally and in the cloud for redundancy. The inclination angle of the PV system is 10°. The installed PV has a fixed inclination and is without any tracking system. This setup is similar to the generally available rooftop system, which we can expect in a normal house.
 |
Figure 8 Roof-top panels and the data logging system. |
Figure 9 shows the maximum, minimum, and an average of PV generation data logged. It is observed that the minimum generation is zero, which represents load shedding of the locality and the PV system installed is a grid-connected system. By getting rid of the load-shedding samples from the observations, the effect of load-shedding on the generation data is taken away.
 |
Figure 9 Roof-top PV generation data. |
The PV system is equipped with a data logger system which can record the PV generation data every 15 min. The recorded power data is post-processed to convert it into per day energy production data. In Figure 10, daily energy production data is compared to a mathematical simulation.
 |
Figure 10 Energy generated per recorded data vs generated sample. |
Figure 10 shows recorded data in red colour and the green solid line shows the simulated PV energy production variation per-day basis. The blue dashed line in the figure represents the average energy production throughout the day. The mean value of the generated sample is 3.1561 kWh and the mean value of the measured data is 3.1422 kWh. The box plot of the two data sets is shown in Figure 11. The close spread of the field data and the generated samples confirms the validity of the mathematical model.
 |
Figure 11 Box plot of sample generated vs real field data. |
5.2 Test study
From Figure 4 it is observed that the PV production is at its peak in the middle of the year when the inclination angle is low. When the inclination angle is increased, the peak PV energy output starts to decrease. At a steep inclination angle, the PV output attains a minimum value in the time period when the lower inclination PV panels reach their maximum value. This counters the behaviour of the PV panel, which shows the rooftop PV panels, which are at a lower inclination angle, and the BIPV system, which are at a higher inclination angle. With the current model of PV production, the optimization models equations (7) and (8) are tested to validate the proposed model.
5.2.1 Single objective study
The proposed research is based upon the utilisation of BIPV system to minimise the variation of the per-day energy production of the PV system. To validate the effectiveness and optimal size of the rooftop system and BIPV for proper integration, the objective function developed in 7 is tested for different rooftop areas. Various test cases which are considered in the research work are given in Section 4.
The objective function defined in equation (7) is solved using two optimization methods. One method is the evolutionary genetic algorithm and another is mathematical non-linear programming. The solution of the genetic algorithm fails to converge to a better solution for test cases 1–3 and 7. The test cases 1–3 consists of small rooftop areas. The mathematical optimization method produces better results as compared to the evolutionary method. A comparison between the two optimization methods is given in Figure 12.
 |
Figure 12 Single objective convergence. |
Thus, the mathematical method is used for solving the single objective problem of minimization of the peak-to-average ratio of the energy production for different test cases. The per-day energy production shown in Figure 10 which varies greatly. The stochastic behaviour creates a large fluctuation, and the optimization function may not converge. The optimal number of PV panels will be decided in the design phase. Therefore, the decision problem is based on the expected value of the energy produced. A sample of mean energy production at any hour is generated while considering the average clarity index at the given PV plant location. In the current test case, the plant location is given in Section 3. The optimal point is validated with the stochastic variation in the clarity index.
The optimization results of the test cases 1–10 are given in Table 1 and Figure 13.
 |
Figure 13 Optimal roof top panels for different test cases. |
As the installation size increases, it is discovered that the optimal choice of roof-top PV and BIPV is not in exact proportion. An increase in the rooftop and facade area leads to a non-linear variation in energy production. A polynomial data fitting is done on the PV panels data set given in Table 2. It is observed that the root mean square error (RMSE) is 0.5682 at first order and the error decreases to 0.5654 when polynomial order increases to 2. Further, an increase in polynomial order also increases the RMSE to 0.6005. Thus, the relation between the number of roof top vs BIPV can be approximated with second-order polynomial (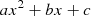 ) where, a = 0.002145, b = 1.401 and c = 0.8097.
) where, a = 0.002145, b = 1.401 and c = 0.8097.
Optimal number of PV panels for BIPV and roof-top system.
The per-day energy production for different test cases is given in Figure 14. The result confirms that with the optimal choice of the BIPVs and the roof-top modules, a flat energy production profile is achieved. The peak and the valley in the result correspond to the only roof-top system and the only BIPV system installation, respectively. These are the two extremes, unoptimized cases of system installation. Thus, the optimal choice of the module number leads to optimal generation throughout the year. This optimum choice provides a reliable energy production capacity on a daily basis.
 |
Figure 14 Test cases 1–10 for fixed cleanness index. |
In the real world, the flat energy production result of an ideal PV installation might not be ideal. PV production is stochastic, which can lead to dynamic variation in the production of electrical energy. Thus, to validate the applicability of the proposed simplified method for PV system installation, the authors tested the result with a stochastic variation. The cleanness index’s stochastic variation reflects pollution, cloudy or rainy days, and so on. These variations are not in the control of human beings, and they will affect the PV generation. The result of the optimal choice for different installation areas under stochastic conditions is shown in Figure 15.
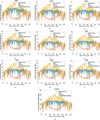 |
Figure 15 Test cases 1–10 for variable cleanness index. |
5.2.2 Multi-objective study
In the single objective decision, the best choice of roof-mounted PV and BIPV was much less than the installation capability of the building infrastructure. In the real world, the decision on PV installation size cannot be determined, only by equation (7). To mitigate the issues of a single objective approach, a multi-objective decision criterion is considered, which can provide multiple optimal choices to the designer for PV installation. The two different objectives are; the minimization of electrical energy variation and maximum utilization of PV installation area. Pareto-optimal results for different test cases are given in Figure 16. The y-axis represents increased rooftop utilisation, while the x-axis represents the minimisation of peak-to-average ratio (Fig. 16). From the result, it can be confirmed that any improvement in any of the two objective values leads to a decrease in the other fitness values. This confirms the non-domination of the solution to equation (8).
 |
Figure 16 Pareto optimal results for different test cases. |
From the observed result, it can be confirmed that with an increase in the rooftop installation area, the optimum set of the non-dominated solution shrinks. Furthermore, the peak-to-average ratio range begins to narrow, resulting in fewer options for installation size. Overall, it can be safely stated that with an increase in the size of PV plants leads to poor performance of objective 1, i.e., the variation in per-day energy production will increase.
This non-dominated behaviour can provide guidelines to designers if the project installation is in different phases. The system operation can still operate in an optimal region. The benefit of this approach is that a large plant installation project can be split into multiple phases. Each phase size can be selected from the Pareto-optimal curve. In this way, the project of PV installation can operate in an optimal region even if the system requirements do not need to be fulfilled on an urgent basis.
5.2.3 Radial distribution network test
After validating the PV generation model in the previous section, the proposed solution must be validated in a test distribution network. This test aims to verify the applicability and proposed benefit of the BIPV and rooftop system in a real-life scenario. To validate this, a plant and controller model is implemented on a programmable logic controller (PLC).
A human-machine interface (HMI), as shown in Figure 17 is developed to monitor the roof-top and BIPV performance during the operation period. The PlC’s analogue measurement block is used to measure and log the power output, energy import, voltage, and angle of the local node of the BIPV and rooftop systems. The HMI provides a very simple and intuitive visual interface for the end user to interact with the PV plant. The load profile of the distribution network is considered a mixture of 30% industrial and 70% domestic load. A 24-hour load profile with an hourly variation of 10% and 10% day-to-day variation is considered. Seasonal effects are also taken into account during the winter and summer seasons.
 |
Figure 17 B&R automation studio human machine interface (HMI). |
The installation types of PV i.e. roof-top-only (RTO), BIPV-only (BIO), and optimal BIPV+roof-top (OBIRT) are tested on the IEEE-33 bus. Figure 18 depicts the per-day electrical energy import from the grid to the local load. It is observed that when the PV installation type is roof-top only, then the grid dependency for the end user is minimal. The grid dependency is the same for all RTOs (BIO and OBIRT) at the start of the year. Due to the angular inclination orientation of the sun with respect to the installation location, the grid import for the BIO installation began increasing in the middle of the year, while the grid import for the RTO installation began decreasing. This result is in agreement with the results shown in Figure 15. The nodal voltage fluctuates with the PV generation. The minimum and maximum nodal voltages are 0.9–1.0, which is within an acceptable range of nodal voltage deviation.
 |
Figure 18 Grid dependency. |
The energy import from the main grid is minimal for an RTO type of installation, but the system installation size is very large to achieve grid independence. The utilization of installed capacity is not done properly. Most PV generation is either injected into the grid or curtailed. In the current situation, the PV is operating in load-following mode, where the power output of the PV is adjusted to satisfy the local load demand. The PV power injection is not acceptable for grid stability reasons. Thus, zero power injection mode restricts the PV installation’s capacity reduction. In this situation, the OBIRT is performing as a trade-off between PV utilisation and grid dependency.
Figure 19 depicts the PV power curtailment in zero grid injection mode. The BIO installation will have maximum utilisation since the generation capability of the system is less than local demand. It can be observed that the BIO’s power is curtailed at the beginning and end of the year, when its power output is at its maximum. The RTO system will be reduced for the majority of the year. The fluctuation in the curtailment is due to load demand variation and PV generation uncertainties. Overall, it can be easily concluded that the RTO type of installation is beneficial to the end-user when the gird-import is acceptable, but uncertainty in the PV production will create a stability issue for the gird. The optimal combination of BIPV and a roof-top system, on the other hand, will produce a trade-off solution that minimises grid dependency while increasing installation costs throughout the year due to less curtailment.
 |
Figure 19 PV power curtailment. |
6 Conclusion
PV is becoming an increasingly important component of the electric energy requirements. The movement of the earth around the sun has an impact on PV energy production. This motion of the earth leads to a variation in electrical energy throughout the year. The roof-top PV plant and facade-based BIPV system are not free from this inherent issue.
In this paper, the authors investigated this issue of energy production over a year and proposed a solution to minimise this effect. The proposed solution is tested on the IEEE-33 bus radial distribution system. An optimal integration of BIPV and roof-top PV systems minimizes the issue of energy production variation. A smooth energy production profile is obtained, which minimises the grid dependency of the end user and maximizes the PV installation.
In this paper, the PV installation is targeted based on the rooftop area of the end user. The grid injection from the end user into the grid is not considered. Further work can be done to include the grid injection by the end user, which can further add benefit to the user. The flat energy profile will help the user store energy in small spaces and could save them money.
References
- Franco S., Mandla V.R., Rao K.R.M. (2017) Urbanization, energy consumption and emissions in the indian context a review. Renew. Sust. Energy Rev. 71, 898–907. [CrossRef] [Google Scholar]
- Li M., Shan R., Hernandez M., Mallampalli V., Patiño-Echeverri D. (2019) Effects of population, urbanization, household size, and income on electric appliance adoption in the chinese residential sector towards 2050. Appl. Energy 236, 293–306. [CrossRef] [Google Scholar]
- Han J., Fontanos P., Fukushi K., Herath S., Heeren N., Naso V., Cecchi C., Edwards P., Takeuchi K. (2012) Innovation for sustainability: toward a sustainable urban future in industrialized cities. Sustain. Sci. 7, 1, 91–100. [CrossRef] [Google Scholar]
- Saygin D., Kempener R., Wagner N., Ayuso M., Gielen D. (2015) The implications for renewable energy innovation of doubling the share of renewables in the global energy mix between 2010 and 2030. Energies 8, 6, 5828–5865. [CrossRef] [Google Scholar]
- Keramidas K., Diaz Vazquez A., Weitzel M., Vandyck T., Tamba M., Tchung-Ming S., Soria-Ramirez A., Krause J., Van Dingenen R., Chai Q., Fu S. (2020) Global energy and climate outlook 2019: electrification for the low-carbon transition, Publications Office of the European Union, Joint Research Center, Luxembourg. [Google Scholar]
- Sterner M. (2009) Bioenergy and renewable power methane in integrated 100% renewable energy systems. Limiting global warming by transforming energy systems, vol. 14, Kassel University Press GmbH. [Google Scholar]
- Tang J., Ye B., Lu Q., Wang D., Li J. (2014) Economic analysis of photovoltaic electricity supply for an electric vehicle fleet in Shenzhen, China. Int. J. Sustain. Transp. 8, 3, 202–224. [CrossRef] [Google Scholar]
- Alqahtani N., Balta-Ozkan N. (2021) Assessment of rooftop solar power generation to meet residential loads in the city of Neom, Saudi Arabia. Energies 14, 13, 3805. [CrossRef] [Google Scholar]
- Sahu A., Yadav N., Sudhakar K. (2016) Floating photovoltaic power plant: a review. Renew. Sust. Energy Rev. 66, 815–824. [CrossRef] [Google Scholar]
- Freitas S., Brito M.C. (2019) Solar façades for future cities. Renew. Energy Focus 31, 73–79. [CrossRef] [Google Scholar]
- Shukla A.K., Sudhakar K., Baredar P., Mamat R. (2018) BIPV based sustainable building in South Asian countries. Sol. Energy 170, 1162–1170. [CrossRef] [Google Scholar]
- Asif M., Hassanain M.A., Nahiduzzaman K.M., Sawalha H. (2019) Techno-economic assessment of application of solar PV in building sector: a case study from Saudi Arabia. Smart Sustain. Built Environ. 8, 1, 34–52. https://doi.org/10.1108/SASBE-06-2018-0032. [CrossRef] [Google Scholar]
- Denholm P., Margolis R.M. (2007) Evaluating the limits of solar photovoltaics (PV) in traditional electric power systems. Energy Pol. 35, 5, 2852–2861. [CrossRef] [Google Scholar]
- Chauhan R.K., Gonzalez-Longatt F., Rajpurohit B.S., Singh S.N. (2018) DC microgrid in residential buildings. DC Distrib. Syst. Microgrids 115, 367–387. [CrossRef] [Google Scholar]
- Jackson T., Oliver M. (2000) The viability of solar photovoltaics. Energy Pol. 28, 14, 983–988. [CrossRef] [Google Scholar]
- Green M.A. (2000) Photovoltaics: technology overview. Energy Pol. 28, 14, 989–998. [CrossRef] [Google Scholar]
- Eiffert P. (2000) Building-integrated photovoltaic designs for commercial and institutional structures: a sourcebook for architects, Diane Publishing. [Google Scholar]
- Kjellsson E. (2000) Potential for building integrated photovoltaics–a study for Sweden. IEA-PVPS Task, pp. 2–4. [Google Scholar]
- Moriarty P., Honnery D. (2016) Can renewable energy power the future? Energy Pol. 93, 3–7. [CrossRef] [Google Scholar]
- Azarpour A., Suhaimi S., Zahedi G., Bahadori A. (2013) A review on the drawbacks of renewable energy as a promising energy source of the future. Arab. J. Sci. Eng. 38, 2, 317–328. [CrossRef] [Google Scholar]
- Crăciun B.-I., Kerekes T., Séra D., Teodorescu R. (2012) Overview of recent grid codes for PV power integration, in: 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), IEEE, pp. 959–965. [CrossRef] [Google Scholar]
- Kenneth A.P., Folly K. (2014) Voltage rise issue with high penetration of grid connected PV. IFAC Proc. Vol. 47, 3, 4959–4966. [CrossRef] [Google Scholar]
- Ye S., Xue P., Fang W., Dai Q., Peng J., Sun Y., Xie J., Liu J. (2021) Quantitative effects of PM concentrations on spectral distribution of global normal irradiance. Sol. Energy 220, 1099–1108. [CrossRef] [Google Scholar]
- Hulstrom R., Bird R., Riordan C. (1985) Spectral solar irradiance data sets for selected terrestrial conditions. Sol. Cells 15, 4, 365–391. [CrossRef] [Google Scholar]
- Zamfir E., Oancea C., Badescu V. (1994) Cloud cover influence on long-term performances of flat plate solar collectors. Renew. Energy 4, 3, 339–347. [CrossRef] [Google Scholar]
- Stanciu C., Stanciu D. (2014) Optimum tilt angle for flat plate collectors all over the world–a declination dependence formula and comparisons of three solar radiation models. Energy Convers. Manag. 81, 133–143. [CrossRef] [Google Scholar]
- Chwieduk D.A. (2009) Recommendation on modelling of solar energy incident on a building envelope. Renew. Energy 34, 3, 736–741. [CrossRef] [Google Scholar]
- Graham V., Hollands K., Unny T. (1988) A time series model for KT with application to global synthetic weather generation. Sol. Energy 40, 2, 83–92. [CrossRef] [Google Scholar]
- Erbs D., Klein S., Duffie J. (1982) Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 28, 4, 293–302. [CrossRef] [Google Scholar]
- Graham V., Hollands K. (1990) A method to generate synthetic hourly solar radiation globally. Sol. Energy 44, 6, 333–341. [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Figure 1 Roof top solar panel. |
| In the text | |
 |
Figure 2 Global extra terrestrial irradiance. |
| In the text | |
 |
Figure 3 BIPV facade based PV system. |
| In the text | |
 |
Figure 4 Energy production at different inclination angle. |
| In the text | |
 |
Figure 5 Pareto optimal curve in a multi-objective optimization. |
| In the text | |
 |
Figure 6 The maximum number of PV that can be installed on roof-top and facade. |
| In the text | |
 |
Figure 7 Modified IEEE-33 bus radial distribution network. |
| In the text | |
 |
Figure 8 Roof-top panels and the data logging system. |
| In the text | |
 |
Figure 9 Roof-top PV generation data. |
| In the text | |
 |
Figure 10 Energy generated per recorded data vs generated sample. |
| In the text | |
 |
Figure 11 Box plot of sample generated vs real field data. |
| In the text | |
 |
Figure 12 Single objective convergence. |
| In the text | |
 |
Figure 13 Optimal roof top panels for different test cases. |
| In the text | |
 |
Figure 14 Test cases 1–10 for fixed cleanness index. |
| In the text | |
 |
Figure 15 Test cases 1–10 for variable cleanness index. |
| In the text | |
 |
Figure 16 Pareto optimal results for different test cases. |
| In the text | |
 |
Figure 17 B&R automation studio human machine interface (HMI). |
| In the text | |
 |
Figure 18 Grid dependency. |
| In the text | |
 |
Figure 19 PV power curtailment. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.