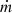| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Power Components For Electric Vehicles
|
|
|---|---|---|
| Article Number | 23 | |
| Number of page(s) | 17 | |
| DOI | https://doi.org/10.2516/stet/2024019 | |
| Published online | 01 April 2024 | |
Regular Article
Thermal management of Li-ion batteries in electric vehicles by nanofluid-filled loop heat pipes
Université de Carthage, Institut National des Sciences Appliquées et de Technologie (INSAT), Laboratoire Matériaux, Mesures et Applications (MMA, LR11ES25), Centre Urbain Nord, 1080 Tunis, Tunisia
* Corresponding author: chaker.zaghdoudi@insat.rnu.tn
Received:
3
November
2023
Accepted:
29
February
2024
An analytical model is developed to determine the thermal performance of a Loop Heat Pipe filled (LHP) with copper oxide–water and alumina–water nanofluids for battery thermal management in electric vehicles. The thermal performances of the LHP are predicted for different heat loads and nanoparticle concentrations. It is demonstrated that for fast charging operation corresponding to a heat load of 150 W, the LHP ensures evaporator temperatures of less than 60 °C for a heat sink temperature of 40 °C. The heat transport capacity of the LHP is enhanced and the evaporator temperature is deceased by augmenting the nanoparticle concentration. The water–CuO nanofluid-filled LHP performs better than the water–Al2O3 nanofluid-filled one. The addition of the nanoparticles increases the LHP total pressure drop and the driving capillary pressure. The capillary limit of the water–CuO nanofluid-filled LHP is hardly affected by CuO nanoparticle concentration until 6% beyond which the capillary limit starts decreasing. For the water–Al2O3 nanofluid-filled LHP, the capillary limit decreases when Al2O3 nanoparticle concentration increases. Beyond 6% Al2O3 nanoparticle concentration, the capillary limit of the Al2O3-filled LHP becomes lower than the water-filled one.
Key words: Loop heat pipes / Lithium-ion battery / Electric vehicles / Nanofluids / Electronics cooling / Modeling / Heat transfer enhancement
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
cpl : Liquid specific heat, J/kg·K
F : Friction coefficient, s/m4
g : Gravity acceleration, m/s2
h : Heat transfer coefficient, W/m2·K
K : Overall heat transfer coefficient, W/m2·K
Kg : Permeability of the grooves, m−2
Kw : Permeability of the wick, m−2
Sg : Spacing between the grooves, m
Tb,fb : Fluid base boiling temperature, °C
Tb,np : Nanoparticle boiling temperature, °C
Greek symbols
ΔPll : Capillary driving pressure, Pa
ΔPll : Liquid pressure drop in the liquid line, Pa
ΔPg : Hydrostatic pressure drop, Pa
ΔPvg : Vapor pressure drop in the groove, Pa
ΔPvl : Vapor pressure drop in the vapor line, Pa
ΔPw : Liquid pressure drop in the wick, Pa
ϕ : Mass concentration of nanoparticles
λ : Thermal conductivity, W/m·K
Subscripts
axw: Axial conduction through the wall
ambcc: Ambient-compensation chamber wall
ambev: Ambient-evaporator wall
R: Compensation chamber (reservoir)
Ri: Compensation chamber inlet
Abbreviations
BTMS: Battery Thermal Management System
FCM: Variable Conductance Mode
VCM: Variable Conductance Mode
1 Introduction
To reduce environmental pollution by decarbonizing road transport, the automotive industries focused on electric vehicle production using batteries, which are considered the heart of these systems. The Lithium-ion (Li-ion) battery is now the main energy storage technology for the automotive industry due to its high energy density, long endurance, and low self-discharge [1]. However, Battery Thermal Management System (BTMS) is important for the electric vehicle industry because it ensures high reliability and safety. Indeed, because of the high recharge power of recent electrical vehicles, the battery’s temperature increases rapidly during charging and can reach high values in some vehicle systems, especially under high-temperature environments. Therefore, Li-ion batteries can risk short circuits, combustion, and explosion. Improving thermal management to ensure battery longevity remains one of the main challenges in developing next-generation vehicles and ensuring sufficient heat transfer from the battery to its environment to maintain an efficient temperature range.
Li-ion batteries must operate at an appropriate temperature range between 25 °C and 60 °C to maintain good cyclic efficiency, state of charge, and overall lifetime [2–4]. Below 25 °C, the Li-ion batteries need to be heated, and above 60 °C, the cells need to be cooled efficiently. Nowadays, battery thermal management is ensured by classical techniques based on heat transfer by conduction and convection, which cannot maintain the battery temperature within the tolerable range. Hence, efforts are focused on active thermal management-based water single-phase cooling systems such as cold plates and air convection. In addition, Research is oriented toward passive two-phase cooling systems such as gravity-assisted heat pipes (thermosyphons) [5], capillary heat pipes including wicks (grooves, screen meshes, or sintered metal power) [6], and oscillating heat pipes [7], vapor chambers [8, 9], and Loop Heat Pipes (LHP) [10–16]. Recent works now focus on hybrid cooling techniques mixing cold plates and heat pipes or loop heat pipe technologies [17].
The LHPs are very efficient cooling systems that can operate at any orientation. They are composed of an evaporator, a vapor line, a condenser, a liquid line, and a compensation chamber (Fig. 1). In a heat pipe, the capillary structure occupies the entire length between the sections of the evaporator and the condenser for which the flows of the liquid and vapor phases are in counter-current. However, in an LHP, the capillary structure occupies the section of the evaporator, which is separated from the condenser thus causing flows of the liquid and vapor phases separated in liquid and vapor lines. Hence, in an LHP, the evaporator is the most important component that includes a capillary wick that creates the necessary capillary driving pressure to ensure liquid return from the condenser to the evaporator through the liquid line. The LHP operation depends on several operating conditions [18, 19]. Many techniques are proposed to increase the two-phase heat transfer within the LHP evaporator. Among them, we can distinguish the porosity and the material of the capillary structure and the working fluid that must be compatible with the LHP materials. The proposed arrangement for the thermal management of the batteries in the electric vehicle is shown in Figure 2. The LHP evaporator absorbs the heat generated by the battery. It is connected to the electric vehicle’s heat ventilation and air conditioning system [14].
1.1 Battery thermal management systems including LHPs
Hong et al. [10] tested three ultra-thin LHPs that differ from each other by the length between the evaporator and the condenser and by the shape of the groove used in the evaporator section. It was demonstrated that all the prototypes allow for an average evaporator temperature below 60 °C under a heat load range between 20 and 80 W. Reducing the evaporator-condenser length and modifying the groove shape lead to a decrease in the evaporator temperature.
Putra et al. [11] conducted an experimental study on the thermal performance of an LHP filled with three different fluids (water, alcohol, and acetone) for three heat fluxes of 0.48, 0.96, and 1.61 W/cm2. They demonstrated that acetone provides the lowest evaporator temperature that remains below 50 °C whatever the imposed heat flux. The temperature of the evaporator obtained with water is the highest and reaches about 60 °C for the maximum heat flux. The evaporator temperatures obtained with alcohol are close to those obtained for water for heat fluxes of 0.48 and 0.96 W/cm2 while they are similar to those obtained with acetone for the heat flux of 1.96 W/cm2.
Ariantara et al. [12] tested an LHP including a capillary structure composed of sintered copper powder. Three heat loads are considered (20 W, 30 W, and 40 W). The experimental results show that for a heat input of 20 W, the battery surface temperature can be kept under 50 °C. For heat input powers of 30 W and 40 W, the battery surface temperature is 60 °C and 68 °C, respectively.
Bernagozzi et al. [13] tested an LHP filled with ethanol and water to validate a numerical code they developed for the BTMS they proposed. The experimental results carried out under highway or fast charging conditions (0.2–0.8 SOC in 10 min) showed that the proposed BTMS is more efficient in reducing the maximum temperature than conventional liquid cold plates. A peak temperature of 31.5 °C is reached when ethanol is used as working fluid, constituting a 3.6 °C temperature reduction compared to cold plates.
Bernagozzi et al. [14] proposed an innovative cooling system comprising graphite sheets and a LHP, filled with NovecTM 649. An experimental demonstrator of a three-cell module was built to compare the thermal performance of the cooling system filled with NovecTM 649 to those obtained with the same cooling system filled with ethanol. Testing on a fast charge drive cycle showed that NovecTM 649 gave faster start-up and a slightly higher maximum temperature, showing that the safety gains and reduction in environmental impact brought by the use of NovecTM 649 came without reducing the thermal performance of the cooling system. Finally, the LHP was tested under three different charging speeds (1C, 2C, and 3C), resulting in maximum temperatures of 28.4 °C, 36.3 °C, and 46.4 °C, respectively, which remain lower at the safety threshold of 60 °C.
Singh and Nguyen [15] tested two types of LHP designs. A miniature version, with a flat disc evaporator, to cool the electronic control unit with a 70 W chipset to keep the source temperature below 100 °C. Two larger versions with cylindrical evaporators were tested for power electronics and battery cooling, with carrying capacities over 500 W.
Hashimoto et al. [16] proposed using the LHP concept as a heating device. The evaporator is heated to start the LHP operation and the condenser absorbs the heat dissipated by the battery, and as the vapor temperature in the condenser section is higher than that of the battery surface, condensation happens, and the condensate flows back to the evaporator by the driving capillary pressure. This enables to heat the battery in harsh weather conditions in winter when the temperature in many countries is below 0 °C.
The operating conditions in the previously mentioned experimental works are listed in Table 1. We can conclude that the LHP-based BTMS allows for battery surface temperature lower than 60 °C for heat loads up to 150 W, cooling temperature range between 20 °C and 30 °C. The LHP thermal resistance varies between 0.1 K/W and 1 K/W, and the LHP is filled with water, alcohol, acetone, Novec 649. Only Hashimoto et al. found battery temperature higher than 60 °C with an LHP filled with R134a.
Main experimental studies on BTMS including LHPs.
1.2 Nanofluid-filled LHPs
A new issue is to improve the thermal properties of the working fluid by suspending small solid particles in the fluid so-called nanofluids. Hence, the nanofluids’ thermal conductivity and heat capacity are higher than those of common fluids. There is a lot of experimental research on using nanofluids in the automotive industry [20]. The percentage of the experimental works according to automobile components is as follows: automobile radiator coolant (45.7%), engine fuel (25.8%), automobile engine lubricant (20.8%), air conditioning system lubricant (5%), shock absorber (1.6%), and brake fluid (1.6%). Note that experimental studies dealing with the use of nanofluids in battery thermal management are scarce [21]. Pure metal oxide nanofluids are the most used in battery thermal management systems and the most used base fluid is water [21].
Gunnasergaran et al. [22] tested a flat LHP with vapor and liquid lines made of transparent tubes to visualize the working fluid flow patterns. In their experimental studies, they evaluated the thermal performances of an LHP using (SiO2–H2O) nanofluid and compared them with pure water for heat input ranging between 20 W and 100 W. The results indicate that the nanofluid-filled LHP total thermal resistance decreases by 28–44% when compared to a pure water-filled LHP by suspending a SiO2 mass concentration of 3%.
Gunnasergaran et al. [23] tested an LHP filled with Al2O3–H2O with nanoparticle mass concentrations ranging from 0% to 3%. The experimental results reveal that the thermal resistance of the LHP filled with nanofluid with nanoparticle concentrations of up to 1% decreases by 5.5% compared to that of the LHP filled with pure water. However, no further decrease was observed with nanoparticle concentration above 1% and it was concluded that the optimum nanoparticle concentration is 1%.
Putra et al. [24] tested an LHP including biomaterial (Collar) and sintered powder metal capillary structures filled with Al2O3–H2O nanofluid or pure water. The experimental results showed that the temperature difference between the evaporator and condenser is lowered by using the biomaterial when compared to that obtained with sintered powder. The utilization of nanofluid also decreases the temperature difference.
Gunnasergaran et al. [25] conducted experiments on an LHP filled with water-based SiO2 nanofluid. The tests reveal that there exists an optimum mass concentration equal to 0.5% for which the LHP thermal resistance is minimum whatever the heat input power. Design-Expert software demonstrated that the optimal nanoparticle mass concentration and heat input power are 0.48 and 60 W, respectively.
Wan et al. [26] tested a water-based Cu nanofluid. It was demonstrated that 12.8% and 21.7% reductions in wall evaporator temperature and LHP thermal resistance, respectively are obtained, and the optimum mass concentration is 1.5%.
Tharayil et al. [27] used graphene water in a miniature LHP. The results showed a lower thermal resistance and evaporator interface temperature compared to pure water at 380 W for the optimum mass concentration of graphene.
Gunnasergaran et al. [28] studied the effect of Fe2NiO4–H2O nanofluid on the heat transfer enhancement of an LHP installed in a real desktop PC CPU. Experimental investigations indicate that the core temperature of the CPU is lowered by 5.7 °C when the nanofluid-filled LHP is used instead of the water-filled LHP. Besides, it is demonstrated that the optimal mass concentration of Fe2NiO4 that enables obtaining the optimal thermal performance is about 1%.
Gunnasergaran et al. [29] tested LHP charged with diamond–H2O nanofluid with nanoparticle mass concentrations ranging from 0% to 3%. They have proven that the evaporator temperature decreases when using this nanofluid if compared to that charged with pure water for heat input ranging from 20 W to 60 W. Besides, the steady-state evaporator temperature for the diamond–H2O-filled LHP is reached rapidly when compared to that for the water-filled LHP. They conclude that using the nanofluid reduces the response time of the LHP.
Akshay et al. [30] conducted experimental investigations on LHP filled with Al2O3–H2O nanofluid. It was concluded that adding the alumina nanoparticles in water causes a decrease in the evaporator temperature for heat input powers ranging from 30 W to 310 W.
Wang et al. [31] carried out experiments on an LHP filled with Cu–H2O nanofluid. For a nanoparticle mass concentration of 1.5%, the experimental results showed that a high reduction in the LHP thermal resistance is obtained for low heat loads less than 25 W when compared to that obtained from a pure water-filled LHP. For high heat input powers, the decrease in the nanofluid-filled LHP thermal resistance is lowered. In addition, increasing the nanoparticle concentration above 1.5% deteriorates the nanofluid-filled LHP thermal performance when compared to the pure water-filled LHP.
Stephen et al. [32] have carried out a comparative study of the heat transfer performance of a compact LHP using pure water, Al2O3–H2O, and Ag–H2O nanofluids as working fluids. The tests demonstrate that LHP thermal resistance reductions of 34.7% and 20.2% were obtained for 0.12% in volume concentration of Ag and Al2O3, respectively. The suspension of a small amount of Ag nanoparticles in the base fluid improved the operating temperature range by 15% when compared with that of alumina nanofluid.
Bin Harun et al. [33] conducted experiments on an LHP filled with three types of nanofluids (diamond–H2O, Al2O3–H2O, and SiO2–H2O). The results reveal that the LHP thermal resistance decreases when augmenting the nanoparticle concentration for diamond–H2O and Al2O3–H2O nanofluids. However, for SiO2–H2O nanofluid, the opposite trend was observed. All the tested nanofluids give better LHP thermal performance when compared to those of the LHP filled with pure water. Moreover, the diamond nanofluid allows for a better thermal enhancement with a 1.19% mass concentration.
Riehl and Murshed [34] tested an LHP filled with NiO–H2O nanofluid. The results indicated that a slight heat transfer improvement is obtained when suspending nanoparticles in water. However, the water-filled LHP gave better results when compared to the NiO–water-filled LHP for low heat loads.
Veeramachaneni et al. [35] tested an LHP filled with a copper–graphene–H2O hybrid nanofluid with two ratios (30:70 and 70:30) and two volume nanoparticle concentrations were considered (0.01% and 0.02%). The results reveal that the suspension of hybrid nanoparticles in water increases the capillary limit by up to 37% and decreases the thermal resistance and evaporator temperature by up to 24.4% and 10%, respectively.
Table 2 lists the main experimental studies on nanofluid-filled LHPs. From this overview, the following conclusions can be drawn
-
The nanoparticles that are considered in the studies are Al2O3, Ag, Cu, Diamond, Fe2NiO4, Graphene, Cu, Graphene, NiO, and SiO2 with mass concentrations up to 3.5%.
-
Heat loads up to 500 W are envisaged in these studies.
-
Reduction in thermal resistance ranges from 3% [33] to 60% [31].
-
Reduction in evaporator temperature ranges from 10% [35] to 12.8% [26].
-
An increase in capillary limit up to 37% is measured [35].
-
The LHP thermal performance is altered above an optimal mass concentration [26, 28, 31].
Main experimental studies on nanofluid-filled LHPs.
1.3 BTMS Based on nano-filled LHPs and paper goal
The use of nanofluids in two-phase cooling systems (heat pipes and loop heat pipes) for BTMS is under active research. If experimental studies concerning the use of nanofluids in LHPs are scarce, those concerning the use of nanofluids in LHPs with a view to an application for BTMS have not yet been published to our knowledge as it is indicated in Section 1.1. Likewise, studies focusing on the modeling of LHPs filled with nanofluids are scarce [36, 37].
In this study, a complete analytical steady-state model of an LHP is developed to determine the influence of nanofluids on the thermal performance of a flat loop heat pipe proposed for lithium-ion battery thermal management (LF173F163B) of which the technical, thermal, and geometrical characteristics are provided in Table 3. The LHP must ensure an operating temperature below 60 °C for fast charging powers. The proposed arrangement is that of Figure 3. The LHP absorbs heat below the battery cells to release it into the cold source (air or water). The work aims to study the effect of the concentration of nanoparticles on the thermal and hydraulic performances of the LHP to satisfy the thermal operating conditions of the battery cell. Two nanofluids are considered: H2O–CuO nanofluid, which is not experimented yet on LHP operation, and H2O–Al2O3 nanofluid, which was widely used in experiments on LHP.
 |
Fig. 3 Schematic of the envisaged solution for battery cooling with LHPs. |
Technical, thermal, and geometrical characteristics of the battery LF173F163B.
2 Description of the modeled loop heat pipe
The LHP is composed of a flat evaporator with a compensation chamber placed aside and connected to the heat source (Fig. 2), a condenser to dissipate the heat load, and vapor and liquid lines to transport the working fluid between both components. The wick is made of sintered copper powder and rectangular grooves. The evaporator is oval and flat; its dimensions are such that they fit those of the battery cells. The vapor and water-cooled condenser lengths with an inner diameter of 4 mm are 305 mm and 160 mm, respectively. The liquid line has a length of 810 mm and an inner diameter equal to 3 mm. The wick is made of sintered copper powder with a pore radius of 27 μm, and its porosity is equal to 46%. A cooling plastic jacket through which water is pumped is used to ensure the cooling of the condenser [18].
3 Mathematical formulation of the model
The capillary pressure created in the core of the evaporator must exceed the summation of all pressure drops occurring in each component of the LHP according to [18]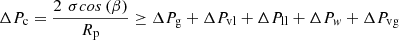 (1)ΔPc is the capillary driving pressure and β is the contact angle. Rp is the pore radius of the wick. ΔPg is the hydrostatic pressure drop and ΔPvl and ΔPll represent the viscous pressure drops in the vapor and liquid lines, respectively. ΔPw represents the liquid pressure drop in the wick, and ΔPvg is the vapor pressure drop in the grooves. When the capillary pressure is equal to or greater than the summation of these pressure losses, the capillary structure can ensure the return of the liquid from the condenser to the evaporator. On the other hand, when the capillary pressure cannot overcome all the pressure losses, the porous structure becomes starved, and dry-out occurs.
(1)ΔPc is the capillary driving pressure and β is the contact angle. Rp is the pore radius of the wick. ΔPg is the hydrostatic pressure drop and ΔPvl and ΔPll represent the viscous pressure drops in the vapor and liquid lines, respectively. ΔPw represents the liquid pressure drop in the wick, and ΔPvg is the vapor pressure drop in the grooves. When the capillary pressure is equal to or greater than the summation of these pressure losses, the capillary structure can ensure the return of the liquid from the condenser to the evaporator. On the other hand, when the capillary pressure cannot overcome all the pressure losses, the porous structure becomes starved, and dry-out occurs.
The hydrostatic pressure is expressed as follows [18]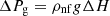 (2)
ρnf is the nanofluid density, ΔH is the height between the condenser and the evaporator, and g is the acceleration gravity.
(2)
ρnf is the nanofluid density, ΔH is the height between the condenser and the evaporator, and g is the acceleration gravity.
The following expressions give the pressure losses in the vapor and liquid phases [18]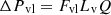 (3)
(3)
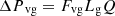 (4)
(4)
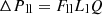 (5)
(5)
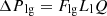 (6)
Lv, Lg, and Ll are the lengths of the vapor line, groove, and liquid line. Fv and Fvg, are the vapor friction coefficients in the vapor line and the grooves. Fll and Flg are the liquid friction coefficients in the liquid line and the grooves, and Q is the heat input power. The expressions of Fvl, Fvg, Fll
, and Flg are given in [18].
(6)
Lv, Lg, and Ll are the lengths of the vapor line, groove, and liquid line. Fv and Fvg, are the vapor friction coefficients in the vapor line and the grooves. Fll and Flg are the liquid friction coefficients in the liquid line and the grooves, and Q is the heat input power. The expressions of Fvl, Fvg, Fll
, and Flg are given in [18].
Darcy’s law calculates the liquid pressure losses in the wick according to [18]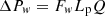 (7)
Lp is the length of the porous structure, and Fw is the liquid friction factor in the porous structure. The expression of Fw is given in [18].
(7)
Lp is the length of the porous structure, and Fw is the liquid friction factor in the porous structure. The expression of Fw is given in [18].
At the evaporator, the heat input power, Qi, is divided into three parts (Fig. 4). The first one, Qaxial, is transferred axially through the evaporator wall by conduction to the compensation chamber; the second one, Qev, is transferred transversally to the interface liquid–vapor at the wick level, and the last one, Qamb, is lost to the ambient if the evaporator is not thermally insulated. Hence, the energy balance at the evaporator can be written as [18]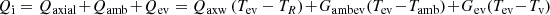 (8)
Tev, TR, Tv, and Tamb are the wall evaporator, the compensation chamber (reservoir), the vapor, and the ambient temperatures, respectively. Gaxw represents the thermal conductance due to axial conduction through the wall between the heated side of the LHP and the compensation chamber. Gev is the thermal conductance between the outer evaporator wall and the vaporization interface at the porous wick surface. Gambev is the thermal conductance between the evaporator wall and the ambient. The expressions of Gaxw, Gev, and Gambev are detailed in [18].
(8)
Tev, TR, Tv, and Tamb are the wall evaporator, the compensation chamber (reservoir), the vapor, and the ambient temperatures, respectively. Gaxw represents the thermal conductance due to axial conduction through the wall between the heated side of the LHP and the compensation chamber. Gev is the thermal conductance between the outer evaporator wall and the vaporization interface at the porous wick surface. Gambev is the thermal conductance between the evaporator wall and the ambient. The expressions of Gaxw, Gev, and Gambev are detailed in [18].
 |
Fig. 4 Heat transfer path in the LHP evaporator and condenser. |
The third term on the right of equation (8) is divided into three parts. The first one represents the latent heat that serves the liquid evaporation, the second one is the sensible heat that serves the heating of the liquid that comes into the evaporator from the compensation chamber, and finally, the third one is the heat transferred to the compensation chamber through the primary wick. Hence, we can write [18]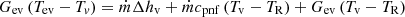 (9)
(9)
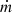 is the mass flow rate circulating through the LHP, ∆hv is the vaporization latent heat, and cpnf is the nanofluid-specific heat. Gcv represents the conductive–convection thermal conductance, calculated using the nanofluid’s energy balance within the porous structure [18].
is the mass flow rate circulating through the LHP, ∆hv is the vaporization latent heat, and cpnf is the nanofluid-specific heat. Gcv represents the conductive–convection thermal conductance, calculated using the nanofluid’s energy balance within the porous structure [18].
At the compensation chamber, a part of the heat flux rate, transported axially by conduction within the evaporator wall and transversally within the porous medium, is transferred by convection to the ambient, and the other part heats the liquid at the entrance of the reservoir, thus we can write [18] (10)
TRi is the condensate temperature at the compensation chamber inlet. Gambcc is the thermal conductance between the compensation chamber and the ambient [18].
(10)
TRi is the condensate temperature at the compensation chamber inlet. Gambcc is the thermal conductance between the compensation chamber and the ambient [18].
The condenser is subdivided into a condensation zone and a sub-cooled zone where the condensate is cooled under the condensation temperature. The energy balance overall of the condenser can be written as [18]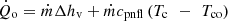 (11)
Tc is the condensation temperature and Tco is the condensate temperature at the condenser outlet.
(11)
Tc is the condensation temperature and Tco is the condensate temperature at the condenser outlet.
For the condensation zone, the energy balance is [18]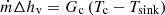 (12)
Gc is the overall thermal conductance between the condensate in the condensation zone and the heat sink, and Tsink is the heat sink temperature [18].
(12)
Gc is the overall thermal conductance between the condensate in the condensation zone and the heat sink, and Tsink is the heat sink temperature [18].
For the sub-cooled zone, the energy balance is expressed as [18]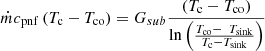 (13)
Gsub is the thermal conductance between the condensate and the heat sink in the sub-cooled zone [18].
(13)
Gsub is the thermal conductance between the condensate and the heat sink in the sub-cooled zone [18].
The energy balance at the liquid line is written as [18]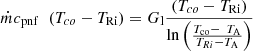 (14)
TRi is the liquid temperature at the inlet of the compensation chamber. Gl is the overall thermal conductance representing the heat transfer between the liquid and the ambient [18].
(14)
TRi is the liquid temperature at the inlet of the compensation chamber. Gl is the overall thermal conductance representing the heat transfer between the liquid and the ambient [18].
The thermal conductivity of the nanofluid, λnf, is a function of the thermal conductivity of the base fluid, λfb, and that of the nanoparticles, λnp, according to Maxwell equation [39]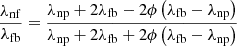 (15)
ϕ is the mass concentration of the nanoparticles.
(15)
ϕ is the mass concentration of the nanoparticles.
The Krieger–Dougherty model is used to calculate the dynamic viscosity, μnf, according to [40]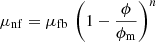 (16)
μfb is the dynamic viscosity of the base fluid.
(16)
μfb is the dynamic viscosity of the base fluid.
Different values of n have been proposed in the literature, from −1 to −4. The exponent n = −2, is the most commonly reported value, and ϕm = 0.64 for the spherical particles.
The density of the nanofluids, ρnf, is calculated from the mixing law in which the nanofluid is assumed homogeneous [41]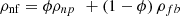 (17)
ρfb and ρnp are the base fluid and nanoparticle densities, respectively.
(17)
ρfb and ρnp are the base fluid and nanoparticle densities, respectively.
To determine the specific heat of nanofluids, the model based on the hypothesis of thermal equilibrium between the particles and the base fluid is considered according to [42] (18)
cpfb and cpnp are the base fluid and nanoparticle heat capacities, respectively.
(18)
cpfb and cpnp are the base fluid and nanoparticle heat capacities, respectively.
The effect of the base fluid and nanoparticles’ boiling temperatures has been considered in the expression of the nanofluid enthalpy of vaporization according to [43]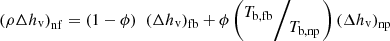 (19)
Tb
,fb and Tb
,np are the fluid base and nanoparticle boiling temperatures.
(19)
Tb
,fb and Tb
,np are the fluid base and nanoparticle boiling temperatures.
The surface tension, σnf, is calculated according to the model proposed by Venkatachalapathy et al. [44]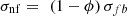 (20)
σfb is the surface tension of the base fluid.
(20)
σfb is the surface tension of the base fluid.
This equation originates from the study of Venkatachalapathy et al. [44] who carried out experiments on a water–CuO nanofluid and demonstrated that the liquid–vapor surface tension decreases with the nanoparticle mass concentration. The authors showed that the contact angle decreases, which is synonymous with an increase in the wettability of the surface, and consequently, the driving capillary pressure increases. Sefiane et al. [45] who studied an ethanol–Al nanofluid demonstrated that the surface tension is not affected by the presence of the aluminum nanoparticles and the contact angle increases with Al nanoparticle concentration. It should be noted that the research work that is interested in the problem of wettability of surfaces in the presence of nanofluids has considered flat surfaces. This is not the case in heat pipes and LHP applications. Thus, the problem of the effect of the addition of nanoparticles on the wettability of surfaces remains a research perspective, particularly in the fields of heat pipes with grooved capillary structures and LHPs. Hence further research should be undertaken to predict the surface tension and contact angles as a function of the nature of the base fluid-nanoparticle combination, the concentration of the nanoparticles, and their sizes. The modeling results presented in this study do not consider variations in the contact angle as a function of the nanofluid.
4 Results and discussion
In this section, we present the results obtained for CuO (ρnp = 6450 kg/m3, cpnp = 561 J/kg·K, λnp = 20 W/m·K) and Al2O3 (ρnp = 3960 kg/m3, cpnp = 561.5 J/kg·K, λnp = 37.1 W/m·K) under different nanoparticle concentrations. The main parameters presented are the variations of the LHP evaporator temperatures, the LHP thermal resistance, the total pressure losses, the capillary pumping pressure, and the capillary limit. They are compared to those obtained with pure water filled-LHP. The following operating conditions are considered: the ambient temperature Tamb = 20 °C, the heat sink temperature Tsink = 40 °C, and the heat transfer coefficient hamb = 10 W/m2·K, and the heat transfer coefficient between the condenser wall and the heat sink is hsink = 12,000 W/m2·K. The main characteristics of the modeled copper-water LHP are listed in Table 4.
Main characteristics of the modeled copper–water LHP.
4.1 Evaporator temperature
The variations of the evaporator wall temperatures are depicted in Figure 5 as a function of the heat input power, for pure water and nanofluids with different CuO and Al2O3 mass concentrations. For both nanofluids and a given nanoparticle concentration, the curves exhibit similar shapes. We distinguish two operation modes: the Variable Conductance Mode (VCM) for which the thermal conductance of the LHP is variable, and the Fixed Conductance Mode (FCM) for which the thermal conductance of the LHP is constant. The curves exhibit minima for a particular heat load so-called transition heat load, which is not affected by nanoparticle concentration and it is equal to nearly 100 W for both nanofluids. The augmentation of CuO and Al2O3 nanoparticle concentration causes a decrease in the evaporator temperature. The effect of the addition of CuO and Al2O3 is more pronounced for the FCM mode than for the VCM mode. Thus, the increase of the nanoparticle concentration induces the decrease of the LHP thermal resistance and provides better performance.
 |
Fig. 5 Variations in the evaporator temperature, Tev, as a function of the heat load, Q: (a) CuO–water nanofluid, (b) Al2O3–water nanofluid. |
For pure water, the evaporator temperature is 60 °C for a heat load of 200 W. This demonstrates that the LHP ensures a lower evaporator temperature than the safety threshold temperature of 60 °C for fast charging operation for which the dissipated heat load is estimated to be in the order of 150 W [17]. When adding CuO nanoparticles, the heat load, for which the threshold temperature of 60 °C is reached, shifts to nearly 250 W, which is obtained for an 8% mass concentration of CuO. For the heat load of 150 W (fast charging heat load), the evaporator temperatures are 56.8 °C and 54.5 °C for water-filled and water–CuO-filled LHP with an 8% mass concentration of CuO, respectively. For water–Al2O3-filled LHP, the heat load, for which the threshold temperature of 60 °C is attained, reduces to approximately 200 W for an 8% mass concentration of Al2O3. For a heat load of 150 W, the evaporator temperature is 55.2 °C instead of 56.8 °C and 54.5 °C obtained with pure water-filled and water–CuO-filled LHP, respectively.
The variations in the difference between the evaporator temperatures of an LHP filled with pure water and that of an LHP filled with the H2O–CuO nanofluid or the H2O–Al2O3 nanofluid are presented in Figure 6 as a function of the heat input power. For the two nanofluids, the difference decreases with the heat load for the VCM mode whatever the nanoparticle concentration while for the FCM mode; it increases with the heat input power. Likewise, for a given power, the temperature difference increases with the concentration of the nanoparticles. This indicates that the addition of CuO or Al2O3 nanoparticles further reduces the evaporator temperature. When the LHP is filled with the water–CuO nanofluid, the temperature reduction is greater. Thus, for the same power of 450 W and the same concentration of nanoparticles, the reduction in the evaporator temperature is approximately 6 °C compared to that obtained with pure water (Fig. 6a). For the water–Al2O3 nanofluid, and the same power, the evaporator temperature decreases by approximately 3.5 °C compared to that obtained for a pure water-filled LHP when the nanoparticle mass concentration of Al2O3 is 8% (Fig. 6b).
 |
Fig. 6 Variations in the temperature difference: (a) Tev(water)–Tev(water–CuO), (b) Tev(water)–Tev(water–Al2O3), and (c) Tev(water–Al2O3)–Tev(water–CuO). |
The variations in the difference between the evaporator temperatures of the LHP filled with the water–Al2O3 and water–CuO nanofluids are presented in Figure 6c. As already noted, the evaporator temperature of the water–Al2O3 nanofluid is higher than that of the water–CuO nanofluid whatever the imposed power and the concentration of the nanoparticles, indicating that the LHP filled by the water–Al2O performs less than that filled by water–CuO nanofluid. The difference decreases with the power in the VCM mode-operating zone (Q < 100 W) while it increases with the power in the FCM operating zone (Q > 100 W). Furthermore, we note that this temperature difference is hardly affected by the nanoparticle concentration whatever the heat load. Thus, for a power of 550 W and a nanoparticle mass concentration of 8%, the evaporator temperature of the LHP filled with water–Al2O3 is higher than that of the LHP filled with the water–CuO nanofluid by 3.3 °C.
4.2 LHP thermal resistance
The variations in the thermal resistance of the LHP are depicted for the water–CuO nanofluid in Figure 7a, and water–Al2O3 nanofluid in Figure 7b, as a function of the imposed power. The thermal resistance of the LHP filled with nanofluid is lower than that filled with pure water. It decreases sharply in the VCM operating zone; while in the FCM operating zone, it remains practically constant. The effect of nanoparticle concentration is more visible in the VCM operating zone than in the FCM operating zone. For the LHP filled with water–CuO nanofluid, the decrease in thermal resistance compared to that of the LHP filled with pure water increases with the concentration of the CuO nanoparticles and it is minimal for the VCM-FCM transition power (Fig. 8a). Thus, for a nanoparticle concentration of 8%, it varies between 13.3% and 21.2%. For the LHP filled with water–Al2O3 nanofluid, the reduction in thermal resistance compared to that of the LHP filled with pure water also increases with the mass concentration of the Al2O3 nanoparticles and it is less significant than that of the LHP filled with the H2O–CuO nanofluid (Fig. 8b). It is minimal for the transition power and varies between 7.2% and 10.4% for an Al2O3 mass concentration of nanoparticles of 8%. The difference between the thermal resistances of the LHP filled with water–CuO and that of the LHP filled with the water–Al2O3 nanofluid increases with the nanoparticle concentration and it is minimal for the transition power. The LHP filled with water–CuO allows the best improvement in thermal performance compared to that of the LHP filled with water–Al2O3 nanofluid, which varies between 3.6% and 14.4% for a nanoparticle mass concentration of 8% (Fig. 9).
 |
Fig. 7 Variations in the LHP thermal resistance: (a) filled with water–CuO, (b) filled with water–Al2O3. |
 |
Fig. 8 Reduction in nanofluid-filled LHP thermal resistance compared to water-filled LHP thermal resistance: (a) when using water–CuO nanofluid, (b) when using water–Al2O3 nanofluid. |
 |
Fig. 9 Reduction in water–CuO-filled LHP thermal resistance compared to water–Al2O3-filled LHP thermal resistance. |
4.3 Pressure drop
The variations in the total pressure drop are depicted in Figure 10 for both nanofluids. The pressure drop increases with power. This increase is greater for the VCM operating mode than for the FCM operating mode. For water–CuO nanofluid, the concentration of the nanoparticles hardly affects the total pressure drop for a given heat load (Fig. 10a). However, for water–Al2O3 nanofluid, the pressure drop increases with the nanoparticle concentration (Fig. 10b).
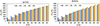 |
Fig. 10 Variations in pressure drop: (a) for water–CuO filled LHP, (b) for water–Al2O3 filled LHP. |
The variations in the difference between the total pressure drops obtained in the case of an LHP filled with water and that filled with water–CuO nanofluid are depicted in Figure 11a as a function of the imposed power. In the power range [50 W–300 W], the difference decreases with the power and practically disappears for Q = 300 W. In this interval, the difference is positive indicating that the total pressure drop in a water-filled LHP is greater than that filled with the water–CuO nanofluid. However, it depends little on the concentration of the CuO nanoparticles. Thus, in this power range, the LHP filled with water has more hydraulic resistance than that filled with water–CuO nanofluid but the difference in hydraulic resistances diminishes with the power and depends little on the concentration of the CuO nanoparticles. For imposed powers greater than 300 W, the total pressure drop of the LHP filled with water–CuO nanofluid becomes greater than that of an LHP filled with pure water (negative difference). Under these conditions, the effect of the concentration of the CuO nanoparticles is more significant and the difference between the total pressure drops widens further with the imposed power but remains lower than that obtained for low powers (Q < 150 W). This indicates that for imposed powers greater than 300 W, the LHP filled with water–CuO nanofluid presents more hydraulic resistance than that filled with water and this hydraulic resistance strongly depends on the concentration of the nanoparticles. With the LHP filled with water–Al2O3 nanofluid (Fig. 11b), we obtain similar trends, namely a greater hydraulic resistance for an LHP filled with pure water for imposed powers ranging between 50 W and 200 W. In this power range, the difference with the hydraulic resistance of an LHP filled with pure water decreases with the power and depends little on the concentration of the Al2O3 nanoparticles to cancel out (equality) for a power of 200 W. Then, a reversal of trend is observed beyond this power, namely a greater hydraulic resistance for a LHP filled with water–Al2O3 nanofluid whose difference with the hydraulic resistance of a water-filled LHP filled increases sharply with the power and concentration of the Al2O3 nanoparticles.
 |
Fig. 11 Variations in (a) ΔPtot(H2O)–ΔPtot(water–CuO), (b) ΔPtot(H2O)–ΔPtot(water–Al2O3), (c) ΔPtot(water–Al2O3)–ΔPtot(water–CuO). |
The difference between the total pressure drop in an LHP filled with water–Al2O3 nanofluid and that in an LHP filled with water–CuO nanofluid increases with the imposed power and the concentration of the nanoparticles (Fig. 11c). It should be noted that the concentration of the nanoparticles considerably affects the total pressure drop in the LHP for high powers. The total pressure drop in the LHP filled with the water–Al2O3 nanofluid is greater than that in the LHP filled with water–CuO nanofluid. This indicates that the LHP filled with water–Al2O3 nanofluid exhibits greater hydraulic resistance and explains the inferiority of its performance compared to that of the LHP filled with the water–CuO nanofluid.
4.4 Capillary pumping
The variations in the difference between the driving capillary pressures of the LHP filled with pure water and that of the LHP filled with water–CuO and water–Al2O3 are presented in Figures 12a and 12b, respectively. This difference is positive demonstrating that the nanofluids provide a higher driving capillary pressure. This difference is not very sensitive to the power but is strongly affected by the concentration of the nanoparticles. Indeed, the difference decreases with the concentration of the nanoparticles showing that the superiority of the nanofluid-filled LHP driving capillary pressure attenuates with the concentration. The driving capillary pressure provided by water–CuO nanofluid is slightly higher than that obtained with water–Al2O3 nanofluid. Indeed, the difference between these two driving capillary pressures is less than 11 Pa for all powers and concentrations of nanoparticles. It increases slightly with concentration, and it diminishes slightly with the power in the VCM operating zone but it increases slightly in the FCM operating zone (Fig. 12c).
 |
Fig. 12 Variations in (a) ΔPc(water–CuO)–ΔPc(H2O), (b) ΔPc(water–Al2O3)–ΔPc(H2O), (c) ΔPc(water–CuO)–ΔPc(water–Al2O3). |
4.5 Capillary limit
The capillary pressure obtained with water is lower than that obtained by adding the nanoparticles. However, the surface tension of the nanofluid is lower than that of water if we take into account equation (20). This is mainly explained by the effect of temperature on the surface tension, which is predominant compared to that of the nanoparticle concentration. Indeed, the temperature levels obtained with water are higher than those obtained with the nanofluid. This leads to a decrease in surface tension greater than that obtained with the addition of nanoparticles. Furthermore, it is observed that the increase in nanoparticles increases the total pressure drop and the capillary driving pressure (Figs. 11 and 12) compared to that obtained with water. Thus, compared to the case of water, the capillary limit (Eq. (1)) increases with the addition of nanoparticles as shown in Figure 13 (intersection of the curve representing the variations of the capillary pressure with that representing the variations of total pressure drop). Thus, it goes from 450 W in the case of water to 550 W for the water–CuO nanofluid with 2% (Fig. 13a), 4% (Fig. 13b), and 6% (Fig. 13c) CuO mass concentrations. However, for 8% CuO mass concentration (Fig. 13d), the capillary limit decreases and it is about 500 W. This shows that increasing further the CuO mass concentration beyond 8% could lead to a decrease in the capillary limit below that obtained with pure water. For water–Al2O3 nanofluid, the capillary limit is higher than that obtained with pure water (Fig. 14). It decreases with the concentration of Al2O3 nanoparticles. Thus, it goes from 550 W for a mass concentration of 2% (Fig. 14a) to 400 W for a mass concentration of 8% (Fig. 14d) (500 W for 4% (Fig. 14b), 450 W for 6% (Fig. 14c)). This shows that the capillary limit becomes lower than that obtained with pure water for mass concentrations greater than 6% in Al2O3.
 |
Fig. 13 Variations of the pressure and the capillary pressure versus heat load: (a) water, (b) 2% CuO, (c) 4% CuO, (d) 6% CuO, and (e) 8% CuO. |
 |
Fig. 14 Variations of the pressure and the capillary pressure versus heat load: (a) 2% Al2O3, (b) 4% Al2O3, (c) 6% Al2O3, and (d) 8% Al2O3. |
5 Conclusion
An analytical model is developed to study the thermal performance of a copper-nanofluid-filled Loop Heat Pipe (LHP) with a flat evaporator operating in steady-state operation in the range of heat loads from 5 to 600 W at a horizontal position. The nanofluids considered in this study are CuO and Al2O3. The LHP is considered for the thermal management of lithium-ion batteries for electric vehicles.
The following conclusions can be drawn:
-
The results indicate that the nanofluid-filled loop heat pipe decreases the evaporator temperature compared to the water-filled loop heat pipe. For the water–CuO-filled LHP, the evaporator temperature reduction is greater than that obtained with water–Al2O3 nanofluid-filled LHP.
-
The threshold safety temperature of 60 °C is reached for Q = 200 W when the LHP is filled with water and Q = 250 W for a LHP charged with water–CuO nanofluid and it is attained for the same heat load (Q = 200 W) as water when the LHP is filled with water–Al2O3 nanofluid.
-
Up to 21% and 10.4% reduction in the LHP thermal resistance are reached with water–CuO and water–Al2O3 nanofluids, respectively. Water–CuO nanofluid allows for the best heat transfer enhancement whatever the heat input power and nanoparticle concentration. It reaches up to 14.4% for a mass nanoparticle concentration of 8%.
-
The CuO mass nanoparticle concentration hardly affects the pressure drop. However, the Al2O3 mass concentration affects sharply the pressure drop in the LHP. Depending on the heat input power range, the pressure drop in a nanofluid-filled LHP can be higher or less than the water-filled LHP pressure drop. The effect of the nanoparticle concentration plays an important role for water–Al2O3 nanofluid rather than water–CuO nanofluid. The pressure drop in a water–Al2O3-filled LHP is greater than that in a water–CuO-filled LHP.
-
The capillary limit is augmented when nanoparticles are added to water. For water–CuO-filled LHP, it increases from 450 W to 550 W when the nanoparticle concentration increases to 6%. Beyond this concentration, the capillary limit is decreased and becomes lower than that of a water-filled LHP for CuO mass concentrations higher than 8%. For water–Al2O3-filled LHP, the capillary limit decreases and becomes lower than that obtained in water-filled LHP when Al2O3 mass concentration is higher than 6%.
The results obtained in this study confirm the magnitudes and trends found in the literature. Specifically, the thermal resistance of the LHP filled with a water–Al2O3 nanofluid is reduced by approximately 10.4% under optimal conditions. This reduction is comparable to the results obtained by Gunnasergaran et al. (5.5%) [23], Stephen et al. (20.2%) [32], and Bin Harun et al. (3%) [33], but not comparable to the findings of Akshay et al. (up to 60% reduction) [30]. It is worth noting that there are no published experiments with water–CuO nanofluid.
Additionally, this study reveals the existence of an optimal nanoparticle concentration that provides the best capillary limit. For the water–CuO nanofluid, the optimal concentration is 8%, while for the water–Al2O3 nanofluid, it is 6%. These values are higher compared to the experimental findings for different nanofluids, which range between 1% and 1.5%. This difference may be attributed to the neglect of surface tension variations with the nature of the nanoparticles due to the lack of data in the literature. The model used in this study considers the effect of nanoparticles on surface wettability through the contact angle, which depends on the nature, size, and concentration of the nanoparticles. The impact of nanoparticles on the evaporation phenomenon and their use in heat pipes and loop heat pipes are important research areas that require further investigation.
References
- Ali M.U., Zafar A., Nengro S.H., Hussain S., Junaid Alvi M., Kim H.-J. (2019) Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation, Energies 12, 3, 446. [CrossRef] [MathSciNet] [Google Scholar]
- Previati G., Mastinu G., Gobbi M. (2022) Thermal management of electrified vehicles-A review, Energies 15, 4, 1326. [CrossRef] [Google Scholar]
- Zhang X., Li Z., Luo L., Fan Y., Du Z. (2022) A review on thermal management of batteries for electric vehicles, Energy 238, 121652. [CrossRef] [Google Scholar]
- Ghaeminezhad N., Wang Z., Ouyang Q. (2023) A review on lithium-ion battery thermal management system techniques: A control-oriented analysis, Appl. Therm. Eng. 219, 119497. [CrossRef] [Google Scholar]
- Wang T., Tan S., Guo C., Su H., Guo C., Jiang Y. (2021) Experimental study on U-shape flat thermosyphon for thermal management of power battery, J. Mech. Sci. Technol. 35, 9, 4193–4200. [CrossRef] [Google Scholar]
- Nasir F.M., Abdullah M.Z., Isamail M.A. (2023) Effect of heat pipe’s configuration in managing the temperature of EV battery, CFD Lett. 15, 3, 22–34. [CrossRef] [Google Scholar]
- Zhou Z., Lv Y., Qu J., Sun Q., Grachev D. (2021) Performance evaluation of hybrid oscillating heat pipe with carbon nanotube nanofluids for electric vehicle battery cooling, Appl. Therm. Eng. 196, 117300. [CrossRef] [Google Scholar]
- Gou J., Liu W. (2019) Feasibility study on a novel 3D vapor chamber used for Li-ion battery thermal management system of electric vehicle, Appl. Therm. Eng. 152, 362–369. [CrossRef] [Google Scholar]
- Liu W., Jia Z., Luo Y., Xie W., Deng T. (2019) Experimental investigation on thermal management of cylindrical Li-ion battery pack based on vapor chamber combined with fins, Appl. Therm. Eng. 132, 114272. [CrossRef] [Google Scholar]
- Hong S., Zhang X., Wang S., Zhang Z. (2015) Experimental investigation on the characters of ultra-thin loop heat pipe applied in BTMS, Energy Procedia 75, 3192–3200. [CrossRef] [Google Scholar]
- Putra N., Ariantara B., Pamungkas R.A. (2016) Experimental investigation on the performance of lithium-ion battery thermal management system using flat plate loop heat pipe for electric vehicle application, Appl. Therm. Eng. 99, 784–789. [CrossRef] [Google Scholar]
- Ariantara B., Putra N., Supriadi S. (2018) Battery thermal management system using loop heat pipe with LTP copper capillary wick, IOP Conf. Ser.: Earth Environ. Sci., 105, 012045. [CrossRef] [Google Scholar]
- Bernagozzi M., Charmer S., Georgoulasa A., Malavasi I., Michè N., Marengo M. (2018) Lumped parameter network simulation of a Loop Heat Pipe for energy management systems in fully electric vehicles, Appl. Therm. Eng. 141, 617–629. [CrossRef] [Google Scholar]
- Bernagozzi M., Miché N., Georgoulas A., Rouaud C., Marengo M. (2021) Performance of an environmentally friendly alternative fluid in a loop heat pipe-based battery thermal management system, Energies 14, 22, 7738. [CrossRef] [Google Scholar]
- Singh R., Nguyen T. (2022) Loop heat pipes for thermal management of electric vehicles, J. Therm. Sci. Eng. Appl. 14, 6, 061010. [CrossRef] [Google Scholar]
- Hashimoto M., Akizuki Y., Sato K., Ueno A., Nagano H. (2022) Proposal, transient model, and experimental verification of loop heat pipe as heating device for electric-vehicle batteries, Appl. Therm. Eng. 211, 118432. [CrossRef] [Google Scholar]
- Singh R., Lappa G., Velardo J., Long P.T., Mochizuki M., Akbarzadeh A., Date A., Mausolf K., Busse K. (2021) Battery cooling options in electric vehicle with heat pipes, Front. Heat Mass Transf. 16, 2. [CrossRef] [Google Scholar]
- Gabsi I., Maalej S., Zaghdoudi M.C. (2018) Thermal performance modeling of loop heat pipes with the flat evaporator for electronic cooling, J. Microelectron. Reliab. 84, 37–47. [CrossRef] [Google Scholar]
- Gabsi I., Maalej S., Zaghdoudi M.C. (2021) Modeling of loop heat pipe thermal performance, J. Adv. Res. Fluid Mech. Therm. Sci. 8, 1, 41–72. [CrossRef] [Google Scholar]
- Patel J., Soni A., Barai D., Bhanvase B. (2023) A minireview on nanofluids for automotive applications: Current status and future perspectives, Appl. Therm. Eng. 219, Part A, 119428. [CrossRef] [Google Scholar]
- Can A., Selimefendigil F., Öztop H.F. (2022) A review on soft computing and nanofluid applications for battery thermal management, J. Energy Storage 53, 105214. [CrossRef] [Google Scholar]
- Gunnasegaran P., Abdullah M.Z., Shuaib N.H. (2013) Influence of nanofluid on heat transfer in a loop heat pipe, Int. Commun. Heat Mass Transfer 47, 82–91. [CrossRef] [Google Scholar]
- Gunnasegaran P., Abdullah M.Z., Yussuf M.Z. (2014) Effect of Al2O3–H2O nanofluid concentration on heat transfer in a loop heat pipe, Proc. Mater. Sci. 5, 137–146. [CrossRef] [Google Scholar]
- Putra N., Saleh R., Septiadi W.N., Okta A., Hamid Z. (2014) Thermal performance of biomaterial wick loop heat pipes with water-base Al2O3 nanofluids, Int. J. Therm. Sci. 70, 128–136. [CrossRef] [Google Scholar]
- Gunnasegaran P., Abdullah M.Z., Yusoff M.Z., Abdullah S.F. (2015) Optimization of SiO2 nanoparticle mass concentration and heat input on a loop heat pipe, Case Stud. Therm. Eng. 6, 238–250. [CrossRef] [Google Scholar]
- Wan Z., Deng J., Li B., Xu Y., Wang X., Tang Y. (2015) Thermal performance of a miniature loop heat pipe using water-copper nanofluid, Appl. Therm. Eng. 78, 712–719. [CrossRef] [Google Scholar]
- Tharayil T., Asirvatham L.G., Ravindran V., Wongwises S. (2016) Thermal performance of miniature loop heat pipe with graphene-water nanofluid, Int. J. Heat Mass Transf. 93, 957–968. [CrossRef] [Google Scholar]
- Gunnasegaran P., Abdullah M.Z., Yusoff M.Z. (2017) Heat transfer in a loop heat pipe using Fe2NiO4-H2O nanofluid, MATEC Web Conf. 109, 05001. [CrossRef] [EDP Sciences] [Google Scholar]
- Gunnasegaran P., Abdullah M.Z., Yusoff M.Z., Kanna R. (2018) Heat transfer in a loop heat pipe using diamond-H2O nanofluid, Heat Transf. Eng. 39, 13–14, 1117–1131. [CrossRef] [Google Scholar]
- Akshay J., Aswin J.J., Jibin J., Rajesh B. (2018) Enhancement of the thermal performance of a loop heat pipe using alumina-water nanofluid: An experimental investigation, IOP Conf. Ser.: Mater. Sci. Eng. Conf. 396, 7p. [Google Scholar]
- Wang X.-W., Wan Z.-P., Tang Y. (2018) Thermodynamic and experimental study on heat transfer mechanism of miniature loop heat pipe with water-copper, Phys. Fluids 30, 027102. [CrossRef] [Google Scholar]
- Stephen E.N., Asirvatham L.G., Kandasamy R., Solomon B., Kondru G.S. (2019) Heat transfer performance of a compact loop heat pipe with alumina and silver nanofluid, J. Therm. Anal. Calorim. 136, 211–222. [CrossRef] [Google Scholar]
- Bin Harun M.A., Gunnasegaran P., Che Sidik N.A., Beriache M., Ghaderian J. (2021) Experimental investigation and optimization of loop heat pipe performance with nanofluids, J. Therm. Anal. Calorim. 144, 1435–1449. [CrossRef] [Google Scholar]
- Riehl R.R., Murshed S.M.S. (2022) Performance evaluation of nanofluids in loop heat pipes and oscillating heat pipes, Int. J. Thermofluids 14, 100147. [CrossRef] [Google Scholar]
- Veeramachaneni S., Pisipaty S.K., Vedula D.R., Brusly Salomon A., Harsha V.S. (2022) Effect of copper-graphene hybrid nanoplatelets in a miniature loop heat pipe, J. Therm. Anal. Calorim. 147, 5985–5999. [CrossRef] [Google Scholar]
- Jose J., Baby R. (2019) Enhancement of the thermal performance of a loop heat pipe using silica-water nanofluid, J. Phys. Conf. Ser. 1355, 1–6, 012010. [CrossRef] [Google Scholar]
- Gabsi I., Saad I., Maalej S., Zaghdoudi M.C. (2022) Modeling of thermal performance of a nanofluid-filled loop heat pipe for battery thermal management in electric vehicles, in 2022 IEEE International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), IEEE, Tunisia, pp. 1–6. [Google Scholar]
- Maxwell J.C. (1881) A treatise on electricity and magnetism, Vol. 1, 2nd edn., Clarendon Press, 13 Oxford, UK. [Google Scholar]
- Einstein A. (1906) Eine neue bestimmung der moleküldimensionen, Ann. Phys. 19, 289–306. [CrossRef] [Google Scholar]
- Krieger I.M., Dougherty T.J. (1959) A mechanism for non-Newtonian flow in the suspension of rigid spheres, J. Trans. Soc. Rheol. 3, 137–152. [CrossRef] [Google Scholar]
- Pak B., Cho Y.I. (1998) Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particle, Exp. Heat Transfer 11, 51–170. [Google Scholar]
- Xuan Y.M., Roetzel W. (2000) Conceptions for heat transfer correlation of nanofluids, Int. J. Heat Mass Transfer 43, 19, 3701–3707. [CrossRef] [Google Scholar]
- Mehregan M., Moghiman M. (2014) Propose a correlation to approximate nanofluids enthalpy of vaporization – a numerical study, Int. J. Mater. Mech. Manuf. 2, 1, 73–76. [Google Scholar]
- Venkatachalapathy S., Kumaresan G., Suresh S. (2015) Performance analysis of cylindrical heat pipe using nanofluids – an experimental study, Int. J. Multiph. Flow 72, 188–197. [CrossRef] [Google Scholar]
- Sefiane K., Bennacer R. (2009) Nanofluids droplets evaporation kinetics and wetting dynamics on rough heated substrates, Adv. Colloid Interf. Sci. 147–148, 263–271. [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Components of the LHP [18]. |
| In the text | |
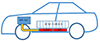 |
Fig. 2 LHP arrangement in the electrical vehicle (reproduced from [14]). |
| In the text | |
 |
Fig. 3 Schematic of the envisaged solution for battery cooling with LHPs. |
| In the text | |
 |
Fig. 4 Heat transfer path in the LHP evaporator and condenser. |
| In the text | |
 |
Fig. 5 Variations in the evaporator temperature, Tev, as a function of the heat load, Q: (a) CuO–water nanofluid, (b) Al2O3–water nanofluid. |
| In the text | |
 |
Fig. 6 Variations in the temperature difference: (a) Tev(water)–Tev(water–CuO), (b) Tev(water)–Tev(water–Al2O3), and (c) Tev(water–Al2O3)–Tev(water–CuO). |
| In the text | |
 |
Fig. 7 Variations in the LHP thermal resistance: (a) filled with water–CuO, (b) filled with water–Al2O3. |
| In the text | |
 |
Fig. 8 Reduction in nanofluid-filled LHP thermal resistance compared to water-filled LHP thermal resistance: (a) when using water–CuO nanofluid, (b) when using water–Al2O3 nanofluid. |
| In the text | |
 |
Fig. 9 Reduction in water–CuO-filled LHP thermal resistance compared to water–Al2O3-filled LHP thermal resistance. |
| In the text | |
 |
Fig. 10 Variations in pressure drop: (a) for water–CuO filled LHP, (b) for water–Al2O3 filled LHP. |
| In the text | |
 |
Fig. 11 Variations in (a) ΔPtot(H2O)–ΔPtot(water–CuO), (b) ΔPtot(H2O)–ΔPtot(water–Al2O3), (c) ΔPtot(water–Al2O3)–ΔPtot(water–CuO). |
| In the text | |
 |
Fig. 12 Variations in (a) ΔPc(water–CuO)–ΔPc(H2O), (b) ΔPc(water–Al2O3)–ΔPc(H2O), (c) ΔPc(water–CuO)–ΔPc(water–Al2O3). |
| In the text | |
 |
Fig. 13 Variations of the pressure and the capillary pressure versus heat load: (a) water, (b) 2% CuO, (c) 4% CuO, (d) 6% CuO, and (e) 8% CuO. |
| In the text | |
 |
Fig. 14 Variations of the pressure and the capillary pressure versus heat load: (a) 2% Al2O3, (b) 4% Al2O3, (c) 6% Al2O3, and (d) 8% Al2O3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.