| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Emerging Advances in Hybrid Renewable Energy Systems and Integration
|
|
|---|---|---|
| Article Number | 71 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.2516/stet/2024075 | |
| Published online | 30 September 2024 | |
Regular Article
Multi-objective cooperative optimization of communication base station and active distribution grid under dual carbon targets
Planning and Development Research Center, State Grid Shanxi Electric Power Company Economic and Technological Research Institute, Shanxi, 030000, China
* Corresponding author: edcftgbhu1234@163.com
Received:
25
July
2024
Accepted:
26
August
2024
To achieve “carbon peaking” and “carbon neutralization”, access to large-scale 5G communication base stations brings new challenges to the optimal operation of new power systems, but also provides new opportunities for the low-carbon development of distribution networks. This paper develops a method to consider the multi-objective cooperative optimization operation of 5G communication base stations and Active Distribution Network (ADN) and constructs a description model for the operational flexibility of 5G communication base stations. Based on this, a multi-objective cooperative optimization 5G communication base station operating model and active distribution network considering the system operation economy and minimum carbon emissions as the optimization objectives are established. In the above model, by encouraging 5G communication base stations to engage in Demand Response (DR), the Renewable Energy Sources (RES), and 5G communication base stations in ADN are concurrently scheduled, and the uncertainty of RES and communication load is described by using interval optimization method. Finally, the problem is solved by combining the equivalent transformation based on interval analysis and the non-dominated sorting genetic algorithm. The analysis results of the example show that participation in grid-side dispatching through the flexible response capability of 5G communication base stations can enhance the power system’s renewable energy consumption and usage efficiency, resulting in significant low-carbon benefits.
Key words: Carbon emission reduction / 5G communication base station / Active distribution network / Multi-objective cooperative optimization
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
As a substantial carbon emitter, the power industry, how to improve the renewable energy source (RES) in the end energy consumption ratio and utilization efficiency, and constructs a new energy system where renewable energy serves as the primary component, aligning with China’s future “dual carbon” energy system goals. In the electricity distribution side, in recent years, the active power supply system has been the most important issue. On the distribution side, the proposed Active Distribution Network (ADN) technology has created good conditions for large-scale distributed RES to be connected to the grid in recent years [1]. However, due to the inherent limitations of the current distribution network structure and the intermittent nature of RES, to attain the objective of full utilization of RES and carbon emission reduction under the framework of ADN, appropriate technical means should be adopted. It is one of the technologies to harness a multitude of flexible resources to participate in the operation and scheduling of the power system [2], to smooth the impact of numerous RES power generation access on the power balance of the system.
Recently, 5G communication base stations have steadily evolved into a key developing load in the distribution network. During the operation process, scientific dispatching and management of power supply and consumption equipment in 5G communication base stations can fully leverage their interactive response potential. This can provide considerable flexibility support to the power grid, ultimately achieving the purpose of reducing the power consumption costs of the base stations themselves while improving the distribution grid for RES consumption and carbon emission reduction [3].
At present, a large number of research results have been made at home and abroad for the problem of optimal operation of ADN containing RES. For example, Reference [4] proposed an active distribution network day-ahead optimal scheduling and operation method considering the risk of operating overrun due to the uncertainty of scenic load and taking into account the scheduling economy and safety. Reference [5] established an ADN optimal scheduling model considering the charging requirements of electric vehicles. Reference [6] studied and proposed an ADN optimal scheduling method that takes into account the interests of different market participants. Reference [7] proposed an innovative decentralized optimization framework for ADN, leveraging the collaborative active and reactive power control capabilities of electric vehicles (EVs) to enhance efficiency and resilience. Reference [8] developed a multi-faceted, hierarchical model for expanding active distribution systems, integrating high-penetration renewable energy and energy storage systems (ESSs) to optimize multiple objectives. Reference [9] introduced a multi-objective ADN operational optimization strategy, emphasizing inter-regional RES consumption through orchestrated distributed generation (DG) active and reactive power control, energy storage equipment charging and discharging, and interruptible load. Reference [10] presented an ADN multi-objective planning framework integrating renewable distributed generation (RDG) and green additional electricity price (GAEP) collaborative optimization, incorporating Demand-side Response’s (DR) load influence and GAEP’s impact on RDG utilization into ADN operational modalities. However, the impact of 5G communication base stations and their flexibility potential is not addressed in any of the above studies. To effectively utilize 5G communication base stations’ low-carbon enabling potential in ADN operation, the impact of their information domain attributes (e.g., communication quality of service) on 5G communication base station operation must be considered in depth. At the same time, a refined descriptive model for the adjustable characteristics of 5G communication base station operation under energy-information multi-domain coupling must be established. In addition, to ensure the effectiveness of the resulting operation scheme, most of the existing studies use stochastic optimization or robust optimization methods to consider the uncertainties in ADN (e.g., fluctuations in RES output or load demand). For example, in [11], an ADN risk taking into account uncertainties is proposed using intelligent soft switches, on-load tap-changers, throwing capacitor banks, energy storage systems, and DR as regulation avoidance stochastic optimization dispatching methods. Reference [12] established an ADN distributed robust optimization dispatching model considering the uncertainty of renewable energy output. In practical applications, stochastic optimization must rely on extensive reliable historical data (sufficient to meet the statistical requirements for hypothesis testing) to extract an accurate description of the uncertainties. However, robust optimization generally focuses only on the uncertainty scenarios that are most detrimental to the achievement of system goals, and the resulting operating strategies are often too conservative. Therefore, the above methods are not well suited to meet the needs of ADN operation decisions with the primary goal of promoting RES utilization.
To address the above problems, this paper proposes a multi-objective interval optimization scheduling method that utilizes the operational flexibility of 5G communication base stations to enhance the low-carbon benefits of ADNs. The method integrates the flexibility of 5G communication base stations into ADN operation scheduling by considering their energy consumption management and the flexible scheduling capability of internal energy storage batteries. On this basis, employs the interval method to address RES output and communication load uncertainties, facilitating a synergistic optimization of the system economy and low-carbon benefits within the operational strategy. According to the characteristics of the proposed model, rewritten as a deterministic multi-objective problem utilizing interval sequential relationships and the possibility degree approach, and then solved by the NSGA-II algorithm. Simulation outcomes confirm the efficacy of the proposed approach.
The rest of this paper is structured as follows: Section 2 addresses the basic structure of 5G communication base station and analyzes its site-network interaction potential; Section 3 builds a multi-objective operational optimization model for active distribution network with 5G communication base stations; The NSGA-II solution method based on interval order relation and probability method is developed in Section 4; Extensive experiments and results under diverse scenarios are presented in Section 5, culminating in the conclusions of the paper.
2 Basic components of 5G communication base stations and potential for station-network interaction
Figure 1 illustrates the equipment composition of a typical 5G communication base station, which mainly consists of 2 aspects: a communication unit and a power supply unit. Among them, the former mainly includes an active antenna unit (AAU), baseband processing unit (BBU), and signal transmission equipment (e.g., optical fiber), while the latter mainly includes distribution grid access power and energy storage battery.
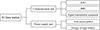 |
Fig. 1 Equipment composition of 5G communication base stations. |
Due to the characteristics of 5G communications, regarding power consumption and the count of base stations, 5G communication base stations exhibit a marked superiority over 4G base stations [13]; in addition to ensuring the reliability of communication services, 5G communication base stations are generally equipped with a certain capacity of energy storage batteries to serve as an emergency power source in case of power supply interruptions on the grid – the above factors provide a wide scope for 5G communication base stations to These factors provide a wide scope for 5G communication base stations to participate in grid interactions [14]. Specifically, on the one hand, 5G communication base station operators can adjust their own power consumption in real-time through various operational control tools [15] (e.g., arranging transceiver start/stop, power regulation, etc.) to engage in power DR; on the other hand, 5G communication base stations can also use their internal energy storage batteries to charge and discharge to engage in grid optimization and enhance the system’s ability to consume RES while ensuring their own power supply and communication service quality.
3 Multi-objective operational optimization model for active distribution network with 5G communication base stations
3.1 Modeling the operational characteristics of 5G communication base stations
3.1.1 Model of 5G communication base station energy consumption
Overall, 5G communication base stations’ energy consumption comprises static and dynamic power consumption [16]. Among them, static power consumption pertains to the reduction in energy required in 5G communication base stations that remains constant regardless of service load or output transmission power. It primarily stems from fixed losses within the power system, including energy consumption in BBU signal processing and cooling systems; dynamic power consumption, conversely, refers to the energy demand that varies with the 5G service load, directly proportional to the output transmission power of the 5G communication base station. In summary, a single 5G communication base station’s total power consumption can be expressed as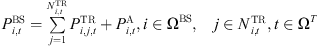 (1)where,
(1)where, 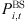 is the cumulative energy usage for the ith base station during timeslot t;
is the cumulative energy usage for the ith base station during timeslot t; 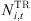 denotes the count of transceivers in an active state, directly correlated to the carrier configuration of the base station;
denotes the count of transceivers in an active state, directly correlated to the carrier configuration of the base station; 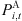 represents the combined power consumption of the power system and the cooling system, etc.; ΩBS is a collection of 5G communication base stations; Ω
T
is the set of time slots. In addition,
represents the combined power consumption of the power system and the cooling system, etc.; ΩBS is a collection of 5G communication base stations; Ω
T
is the set of time slots. In addition, 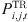 is the power consumption of the jth transceiver of the ith base station in time slot t. According to the literature [17], the formula estimates a transceiver’s energy usage
is the power consumption of the jth transceiver of the ith base station in time slot t. According to the literature [17], the formula estimates a transceiver’s energy usage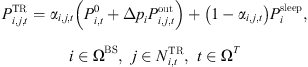 (2)where αi,j,t is the 0-1 variable indicating whether the transceiver is operating or not, and its value is 1 when it is running and 0 when it is sleeping;
(2)where αi,j,t is the 0-1 variable indicating whether the transceiver is operating or not, and its value is 1 when it is running and 0 when it is sleeping; 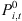 is the no-load power consumption; Δpi is the individual transceiver’s slope with respect to the dynamic power consumption of the load;
is the no-load power consumption; Δpi is the individual transceiver’s slope with respect to the dynamic power consumption of the load; 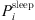 denotes the power usage of the individual transceiver when in sleep mode. In equation (2),
denotes the power usage of the individual transceiver when in sleep mode. In equation (2), 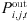 is the base station transceiver’s output transmission power, depends on both signaling and user data power, according to the literature [18], formulated as:
is the base station transceiver’s output transmission power, depends on both signaling and user data power, according to the literature [18], formulated as: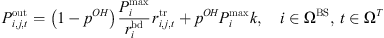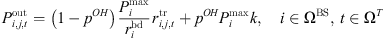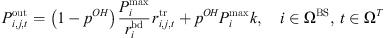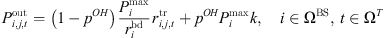 (3)where, p
OH is the proportion of transmitting power accounted for by fixed signaling signals;
(3)where, p
OH is the proportion of transmitting power accounted for by fixed signaling signals; 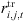 is the quantity of data transport bandwidths; k is a weighted factor reflecting the signaling power intensity of the base station across operational modes, linked to the transceiver’s state and the current bandwidth availability for data transmission [19].
is the quantity of data transport bandwidths; k is a weighted factor reflecting the signaling power intensity of the base station across operational modes, linked to the transceiver’s state and the current bandwidth availability for data transmission [19].
Due to equipment capacity constraints and transmission limitations, the maximum number of transceivers turned on and the number of data transmission broadband in a 5G communication base station should satisfy the following requirements during operation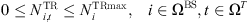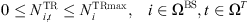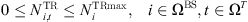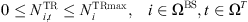 (4)
(4)
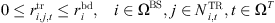 (5)where
(5)where 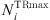 is the number of base station transceivers configured and
is the number of base station transceivers configured and 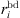 is a single transceiver’s maximum bandwidth utilization.
is a single transceiver’s maximum bandwidth utilization.
3.1.2 Communication service quality characteristics
To ensure the quality of communication services for users in the ADN area [20], the bandwidth capacity provided by the 5G communication base stations in the system needs to meet the required communication load of all users in the area in real-time, which is mathematically expressed as follows: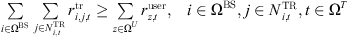 (6)where,
(6)where, 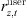 is the throughput demand of the zth user in the communication system at moment t, in Mbps; ΩBS is the set of all base stations in the communication network in the referred area; Ω
U
signifies the count of mobile users within the network area.
is the throughput demand of the zth user in the communication system at moment t, in Mbps; ΩBS is the set of all base stations in the communication network in the referred area; Ω
U
signifies the count of mobile users within the network area.
In addition, for a single 5G communication base station, there is a need to ensure that each user connected to it receives a satisfactory communication load, as shown in the following equation: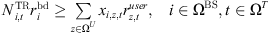 (7)where xi,j,t denotes the 0-1 variable of whether user z is connected to base station i in time slot t.
(7)where xi,j,t denotes the 0-1 variable of whether user z is connected to base station i in time slot t.
3.2 ADN multi-objective operation optimization model considering 5G communication base station access
3.2.1 Objective function
Based on the traditional ADN operation mode, this paper deeply considers the role of interactive response participation of 5G communication base stations in promoting the consumption of distributed RES, which is incorporated into the distribution network operation scheduling model as a flexible resource and determines the optimal coordinated operation strategy of distributed power supply and 5G load resources in the distribution network by combining the power supply cost, system’s operational safety and environmental impact in terms of carbon emissions. For distribution network operators, the optimal operation of ADN should not only reduce the economic cost of system operation but also increase the utilization of RES as much as possible to achieve the reduction of system carbon emissions. Under the current technological level and market conditions, due to the natural contradiction between the above-mentioned economy and the realization of carbon emission reduction objectives, the optimal ADN operation of 5G communication base stations can be summarized as a typical multi-objective optimization problem.
a) Minimization of system operating costs
The operating cost of ADN containing 5G communication base stations mainly includes the cost of power purchase from external markets, the cost of power purchase from internal distributed generation, and the cost of energy storage losses in 5G communication base stations, as calculated by the following equation:![$$ \mathrm{min}{C}^{\mathrm{OPT}}=\sum_{t\in {\mathrm{\Omega }}^T} \sum_{i\in {\mathrm{\Omega }}^{\mathrm{DG}}} {c}_t^{\mathrm{mdg}}{P}_{i,t}^{\mathrm{dg}}\Delta t+\sum_{t\in {\mathrm{\Omega }}^T} {c}_t^{\mathrm{grid}}{P}_t^{\mathrm{grid}}\Delta t+\sum_{t\in {\mathrm{\Omega }}^T} \sum_{i\in {\mathrm{\Omega }}^{\mathrm{BS}}} \left[{\sigma }^{\mathrm{ch}}({P}_{i,t}^{\mathrm{ch}}{)}^2+{\sigma }^{\mathrm{dis}}({P}_{i,t}^{\mathrm{dis}}{)}^2\right] $$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq19.gif) (8)where, ΩDG is the set of distributed power nodes;
(8)where, ΩDG is the set of distributed power nodes; 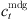 is the cost of purchased power of distributed power;
is the cost of purchased power of distributed power; 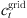 is the price of purchased power from external market;
is the price of purchased power from external market; 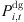 is the actual output value of RES power;
is the actual output value of RES power; 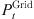 is the purchased power of distribution network; Δt is the duration of a single time period in hours; σ
ch and σ
dis are the loss costs when the energy storage batteries in 5G communication base stations are charged and discharged respectively, which are quadratic functions of charging and discharging power
is the purchased power of distribution network; Δt is the duration of a single time period in hours; σ
ch and σ
dis are the loss costs when the energy storage batteries in 5G communication base stations are charged and discharged respectively, which are quadratic functions of charging and discharging power 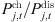 [21];
[21]; 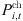 and
and 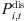 represent the charging and discharging power capacities of energy storage batteries in base stations, respectively and discharge power of the storage battery in the base station.
represent the charging and discharging power capacities of energy storage batteries in base stations, respectively and discharge power of the storage battery in the base station.
b) Minimization of system carbon emissions
To comprehensively capture the carbon emission reduction benefits conferred to the distribution system by 5G communication base stations engaging in DR, this paper takes the minimization of system carbon emissions as another goal of the optimized operation model. Among these, the system’s carbon emission is intimately linked to the consumption of fossil fuels regarding power production, and according to the literature [18], the CO2 emission in the operation and dispatch cycle is equal to its external market power purchase multiplied by the unit generating coal consumption factor and the carbon emission factor on the generation side, as calculated by the following equation: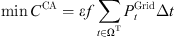 (9)where ε represents coal’s carbon footprint per unit; f represents the coal consumption factor, which is the amount of coal used to generate one unit of electricity in the external grid.
(9)where ε represents coal’s carbon footprint per unit; f represents the coal consumption factor, which is the amount of coal used to generate one unit of electricity in the external grid.
3.2.2 Constraint conditions
a) 5G communication base station operation constraint
The operational constraints of 5G communication base stations studied in this paper mainly include the energy consumption characteristics of the base stations themselves, the communication characteristics, and the operational constraints of their internal energy storage batteries. The models of the energy consumption and communication characteristics of the 5G communication base station have been given in the previous section, thus, this section centers on the modeling of the energy storage batteries utilized in 5G communication base stations.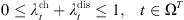 (10)
(10)
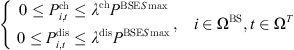 (11)
(11)
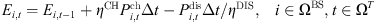 (12)
(12)
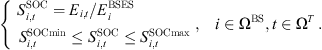 (13)
(13)
Equations (10) and (11) indicate that 5G base station’s energy storage units cannot simultaneously engage in charging and discharging activities during the same time period, and according to reference [18], equation (12) indicates the link between the present stored power of the energy storage devices in the 5G communication base station and the modification of the state of charge and discharge power in the previous period of time during the operation scheduling cycle. Equation (13) represents the constraints that need to be set for the state of charge (SOC) in order to ensure the energy storage battery’s operational life and prevent overcharging and discharging.
In addition, as an energy supply/consumption node in the ADN system, the 5G communication base station needs to satisfy the power equilibrium requirement internally, as shown in equation (14); meanwhile, the interaction power between the 5G communication base station and the distribution network needs to satisfy the constraint shown in equation (15) due to the capacity limitation of the low-voltage distribution substation.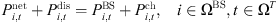 (14)
(14)
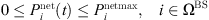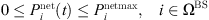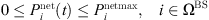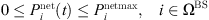 (15)where,
(15)where, 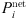 is the power injected from the distribution network to the base station;
is the power injected from the distribution network to the base station; 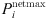 is the maximum limit of interactive power.
is the maximum limit of interactive power.
b) RES power output constraint
The actual power demanded from RES generation for any given time period must not exceed the maximum power capacity available during that period, leading to the imposition of the following constraints: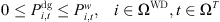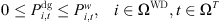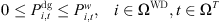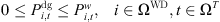 (16)
(16)
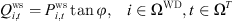 (17)where,
(17)where, 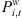 is the predicted value of generated power; ΩWD is the set of RES power composition in ADN, and φ is the power factor angle.
is the predicted value of generated power; ΩWD is the set of RES power composition in ADN, and φ is the power factor angle.
c) Distribution network tide constraints
Analogous to traditional distribution networks, the operation of distribution systems incorporating 5G communication base stations must adhere to active and reactive power flow constraints. Its tidal constraint is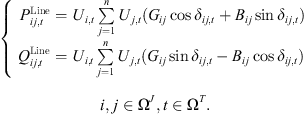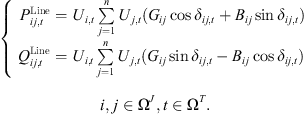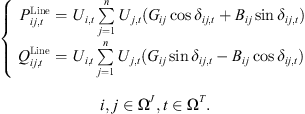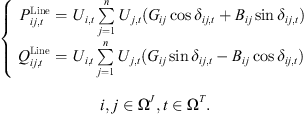 (18)where,
(18)where, 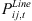 and
and 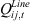 are the active and reactive power flowing from node i to node j at time t, respectively; Ui,t and Uj,t are the voltage amplitudes at node i and node j at time t; Gij and Bij are the conductance and conductance corresponding to line ij; δij,t is the voltage phase angle difference; Ω
J
is the set of distribution network nodes.
are the active and reactive power flowing from node i to node j at time t, respectively; Ui,t and Uj,t are the voltage amplitudes at node i and node j at time t; Gij and Bij are the conductance and conductance corresponding to line ij; δij,t is the voltage phase angle difference; Ω
J
is the set of distribution network nodes.
d) System operation security constraints
To ensure the operational security of ADNs containing 5G communication base stations, the following constraints need to be considered.
The node active/reactive power balance constraint is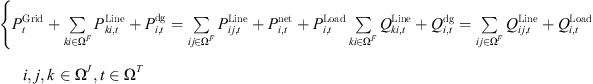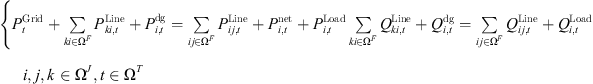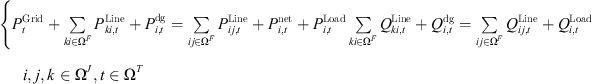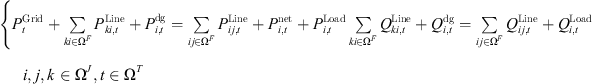 (19)where,
(19)where, 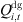 signifies the actual reactive power injected by wind power generation;
signifies the actual reactive power injected by wind power generation; 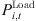 and
and 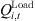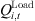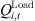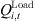 is the active and reactive power demands of the load; Ω
F
is the set of power lines in ADN.
is the active and reactive power demands of the load; Ω
F
is the set of power lines in ADN.
To ensure voltage quality compliance with national standards for end-users, limits need to be placed on the system node voltage excursions, so there are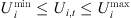 (20)where
(20)where 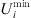 and
and 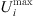 are the minimum and maximum values of the voltage amplitude at node j, respectively.
are the minimum and maximum values of the voltage amplitude at node j, respectively.
3.3 Uncertainty analysis
To address the above ADN multi-objective optimal dispatch model, the values of each parameter in the model need to be determined in advance. For some of these parameters, such as RES generation output and real-time communication load of users, it is often difficult to obtain accurate predicted values about these parameters in advance due to the limitations of prediction means and prediction accuracy, thus bringing significant uncertainties to the model solution. To address these problems, this paper adopts an interval approach to model each uncertainty factor in system operation.
4 Solving method
4.1 Model transformation
For the objective function yi(X, Z) of the multi-objective interval optimization model, the interval ![$ \left[\underline{{y}_i}(X),\overline{{y}_i}(X)\right]$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq49.gif) represents the interval of the objective function value corresponding to the action of the uncertain variable Z at the optimization variable X. Where,
represents the interval of the objective function value corresponding to the action of the uncertain variable Z at the optimization variable X. Where, 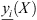 and
and 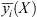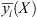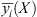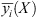 denote the lower and upper limits of the fluctuation of the objective function value, respectively, and can be derived from the following equation [22]:
denote the lower and upper limits of the fluctuation of the objective function value, respectively, and can be derived from the following equation [22]: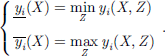 (21)
(21)
For the objective function containing interval parameters ![$ \underset{\mathrm{x}}{\mathrm{min}}\left[{y}_1(X,Z),{y}_2(X,Z)\right]$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq53.gif) , this paper uses the classical interval order relation method, which is equivalently transformed as follows:
, this paper uses the classical interval order relation method, which is equivalently transformed as follows:![$$ \begin{array}{c}\underset{X}{\mathrm{min}}\left[{y}_1\left(X,Z\right),{y}_2\left(X,Z\right)\right]\\ =\underset{X}{\mathrm{min}}\left[\left\langle {y}_1^m(X),{y}_1^w(X)\rangle,\left\langle {y}_2^m(X),{y}_2^w(X)\right\rangle\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq54.gif) (22)where
(22)where ![$ {y}_i^m(X)=\left[\underline{{y}_i}(X),\overline{{y}_i}(X)\right]/2$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq55.gif) and
and ![$ {y}_i^w(X)=\left[\overline{{y}_i}(X)-\underline{{y}_i}(X)\right]/2$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq56.gif) are the midpoint and radius values of the interval, illustrating anticipated advantages of the plan and its responsiveness to uncertainty factors, respectively. In order to satisfy the different tendencies of decision-makers between investment risk-return,
are the midpoint and radius values of the interval, illustrating anticipated advantages of the plan and its responsiveness to uncertainty factors, respectively. In order to satisfy the different tendencies of decision-makers between investment risk-return, 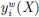 and
and 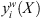 in Eq. (22) are processed by linear weighted summation method, from which the normalized objective function expressions are further obtained as follows:
in Eq. (22) are processed by linear weighted summation method, from which the normalized objective function expressions are further obtained as follows:![$$ \underset{X}{\mathrm{min}}\left[\begin{array}{c}{\phi }_1{y}_1^m(X)+\left(1-{\phi }_1\right){y}_1^w(X),\\ {\phi }_2{y}_2^m(X)+\left(1-{\phi }_2\right){y}_2^w(X)\end{array}\right]. $$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq59.gif) (23)
(23)
For constraints with interval parameters gi(X, Z), the set of values resulting from the action of the uncertain variable Z at the optimization variable X can be represented by the interval quantity ![$ [\underline{{g}_i}(X),\enspace \overline{{g}_i}(X)\enspace ]$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq60.gif) .
.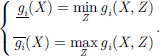 (24)
(24)
Using the interval likelihood approach, the previously discussed constraints with uncertainties are transformed into the following deterministic constraints.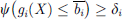 (25)where
(25)where ![$ \overline{{b}_i}=\left[{b}_i^{\mathrm{min}},{b}_i^{\mathrm{max}}\right]$](/articles/stet/full_html/2024/01/stet20240255/stet20240255-eq63.gif) is the value interval of the ith uncertainty constraint; ψ(·) is the interval probability; δi is the probability limit of the ith constraint.
is the value interval of the ith uncertainty constraint; ψ(·) is the interval probability; δi is the probability limit of the ith constraint.
Through the aforementioned method, the initial multi-objective interval optimization model is converted into a standard deterministic multi-objective optimization problem.
4.2 Algorithm flow
In this research, the standard NSGA-II algorithm is applied to address the issue, with Figure 2 detailing the procedure. The main steps of the algorithm are:
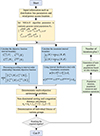 |
Fig. 2 Flowchart of solution procedures. |
Parameter Setup: System input data is loaded, and relevant NSGA-II parameters are configured, including population size, the maximum number of iterations, crossover probability, and mutation probability.
Initial Population Creation: The starting population, or initial solution set (X), is generated using a random function.
Boundary Calculation: The upper and lower limits of each objective function and the constraints are determined using the interval analysis method for different groups.
Calculation of Objective Functions and Constraints: The midpoint and range of the objective function are computed, along with the feasibility of all constraints, to convert the original model into a deterministic form.
Fitness Evaluation: For the deterministic multi-objective optimization problem, the fitness of various groups is assessed. In NSGA-II, fitness includes the number of non-dominated tiers and the crowding distance of individuals within each tier. The population is ranked using a fast non-dominated sorting method, and the crowding distance for each tier is calculated.
Convergence Verification: Convergence is checked to see if the maximum number of iterations has been achieved. If it has, the Pareto optimal solution set is produced. If not, selection, crossover, and mutation operations are conducted on the parent population to generate the offspring population. Using an elitist retention strategy, the next generation is formed based on individual fitness, and the process returns to Step 3.
5 Example analysis
5.1 Parameter setting
The effectiveness of the proposed approach is confirmed through simulation analysis with a modified IEEE-33 [23] bus distribution network as a case study. The issue is tackled using MATLAB R2019b software and solved with the Gurobi 10.0.0 optimizer on a system equipped with an Intel(R) Core(TM) i7-9700 3.0 GHz processor and 16 GB of memory.
According to Figure 3, wind turbines are installed at nodes 4, 10, 13, and 29, each with a capacity of 800 kW. The daily wind power output forecast curve is based on reference [24], with a forecast error of ±20%. Furthermore, 5G communication base stations with energy storage are located at nodes 6, 8, 15, and 31, each group containing 100 base stations, labeled as groups 1, 2, 3, and 4. The fundamental parameters of the base stations are listed in Table 1. The energy storage battery for each base station has a rated capacity of 18 kWh, a maximum charge/discharge power of 3 kW, a SOC range from 10% to 90%, and an efficiency of 0.85.
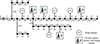 |
Fig. 3 Modified IEEE 33-bus distribution network. |
Basic parameters of 5G communication base stations.
For day-ahead scheduling, the daily variations of communication load and electricity consumption load in the system are shown in Figure 4 according to the reference [25, 26], and the prediction errors are set to ±10% and ±15%, respectively. In the optimization process, the system operation simulation period is taken to be 1 day (i.e., 24 periods) and t = 1 h.
 |
Fig. 4 Curve of system communication load and power load. |
5.2 Analysis of calculation results
5.2.1 Pareto optimal solution
The Pareto frontier set obtained based on the multi-objective interval optimization model in this paper is shown in Figure 5.
 |
Fig. 5 Pareto Frontier set. |
As seen in Figure 5, the carbon emissions are measured in tons, and the resulting optimized solution is well distributed and covers a wide range, which can provide an important reference basis for ADN operation strategy formulation. Further, it can be seen that the operating cost of ADN and carbon emission are closely related. As the economy of the system operating improves, the environmental benefits of the system will decrease. Conversely, when ADN operators pursue the optimal low-carbon benefits, the corresponding operating costs of the system increase. This indicates that the development and utilization of the flexible response potential of 5G communication base stations to promote the utilization of RES and reduce carbon emissions will inevitably lead to the loss of energy storage batteries and the increase of operation and management costs. Thus, the economic cost of system operation increases. Therefore, in actual operation, both of these factors need to be considered according to the needs of decision-makers to arrive at a scientific operation plan that meets the actual requirements.
5.2.2 Analysis of the impact of 5G communication base station flexibility on grid operational efficiency
To assess the impact of 5G communication base stations’ participation in interactive response on ADN benefits, this section contrasts scheduling scenarios with and without 5G base stations’ involvement in DR. In the scenario without DR, base stations do not partake in grid interaction during system scheduling, and their power consumption is managed solely based on their own usage needs.
For each scenario’s Pareto frontier, it is assumed that decision-makers have equal preferences for economic and low-carbon objectives. The unique compromise solution is determined using the approximate ideal solution ranking method [27]. The results of the relevant metrics calculation are presented in Table 2.
Comparison of system operation benefits for different scenarios.
The study indicates that when 5G communication base stations engage in grid optimization and dispatch, the system’s renewable energy source (RES) usage rises by 49.22%. Despite an increase in operational costs, the total carbon emissions decrease. This emission reduction is realized by boosting RES consumption through the flexible response of communication and energy storage systems, thus indirectly lowering the power purchased by the ADN from the main grid.
Figures 6 and 7 depict the system power balance and the curtailed wind power for the two scenarios. These figures demonstrate that 5G base stations optimize the system load profile for improved efficiency, achieving peak-shaving and valley-filling. This enhancement mitigates the mismatch between electricity supply and demand during high and low load periods compared to the scenario without demand response. Moreover, 5G base station flexibility boosts wind power integration, minimizing curtailment during peak generation.
 |
Fig. 6 System power balance. |
 |
Fig. 7 Wind power curtailment curve with and without interactions between 5G communication base stations and power grid. |
This phenomenon mainly arises because 5G communication base stations regulate their energy usage by adjusting their communication equipment, lowering peak load energy usage, and leveraging storage discharge for optimization during high demand and charge during low demand. This strategy boosts RES utilization and reduces power procurement from the main grid. Figures 8 and 9 illustrate the operational results before and after 5G base stations contribute to demand response initiatives.
 |
Fig. 8 Operation optimization results of each base station group. (a) Non-participation in DR operations (b) Participation in DR operations |
 |
Fig. 9 Transceiver scheduling results with interaction of base stations. |
As shown in the Figure 6, when 5G communication base stations do not participate in DR, they act as typical electrical loads. Once 5G base stations are integrated into the system, their energy storage batteries charge during high wind power generation periods to optimize RES usage. During low wind power generation periods, the energy storage batteries provide electricity to the base stations or the grid, minimizing external power procurement for ADN, and thereby curbing emissions from power generation.
As depicted in Figure 10, during peak power load periods, the base stations control the number of active transceivers while preserving communication service quality, significantly lessening 5G base station energy consumption. Integrates energy storage discharge to drastically cut down total power consumption across 5G base station clusters. This decrease inversely aligns with the total system load curve, effectively smoothing peaks and reducing the power purchased from the main grid, thereby improving operational efficiency.
 |
Fig. 10 Comparison results of different optimization schemes. |
5.2.3 Applicability of interval uncertainty analysis method
To demonstrate the superiority of the interval optimization model proposed in this study over traditional methods, this section contrasts the expected benefits of this approach with those of deterministic and robust optimization schemes under real-world conditions. The uncertain parameters are assumed to vary by ±5%, ±15%, and ±25% of the forecasted values, following a uniform distribution. Monte Carlo simulation was employed to generate the sample series for each uncertain variable through random sampling. Based on this, the system operational cost and carbon emissions for the three scenarios were calculated under the given conditions, with the results presented in Figure 10.
From the Figure 10, it is evident that the results obtained through deterministic optimization yield lower expected costs and reduced expected carbon emissions. However, this approach does not account for uncertainty. When examining the variation of actual cost and carbon emissions with uncertainty, it becomes apparent that the optimization targets derived from the deterministic optimization scheme are lower than the actual target values, and this discrepancy grows with increased uncertainty fluctuations.
Both interval and robust optimization methods incorporate operational uncertainty. The robust optimization scheme considers the worst-case scenario, resulting in higher expected costs and carbon emissions compared to actual values, making the results more conservative and less favorable for RES consumption. Conversely, the interval optimization method operates using the median value of uncertain parameters, balancing pessimistic and optimistic scenarios. Consequently, this optimization approach is more reasonable and effective in accounting for uncertainties.
5.2.4 Applicability of interval uncertainty analysis method
This section compares interval optimization with deterministic optimization and robust optimization. Robust optimization refers to the optimization scheme obtained in the worst scenario. Deterministic optimization believes that each element in the uncertain set is represented by the median value. Other parameter Settings in the model are the same as in the previous section, and the weight of the optimization objective remains unchanged.
It is assumed that ±5%, ±15%, and ±25% of the predicted values of uncertain parameters are selected as the variation interval, which conforms to uniform distribution. Monte Carlo random sampling was used to obtain the sample sequence of each uncertain variable, the random simulation times was 5000, and then the economic cost of operation and carbon emissions were calculated, and the results are shown in Table 3.
Comparison of optimal operation under different uncertain methods.
From the Table 3, it is evident that the results obtained through deterministic optimization have lower expected costs and smaller expected carbon emissions. However, this scheme does not account for uncertainty. When observing the actual cost and carbon emissions change with uncertainty, it becomes clear that the optimization targets derived from the deterministic optimization scheme are lower than the actual target values, with the gap widening as uncertainty fluctuations increase.
Interval and robust optimization methods, on the other hand, consider the influence of uncertain factors in operation. The robust optimization scheme, which accounts for the worst-case scenario, results in higher expected costs and carbon emissions compared to the actual situation, leading to conservative optimization results that are not favorable for RES absorption. Conversely, the interval optimization method uses the median value of uncertain parameters, balancing both pessimistic and optimistic scenarios, thus producing a more reasonable optimization scheme.
6 Conclusion
6.1 Concluding remarks
To improve the efficient use of RES resources within an ADN and reduce carbon emissions on the distribution network side, this paper introduces a multi-objective interval optimization method for ADN operations that integrates the low-carbon benefits of 5G communication base stations. Unlike previous studies, this research accounts for the uncertainties of both RES output and 5G communication load. Coordinates distributed power for ADN economic and low-carbon operational gains, the start-stop schedule of 5G communication base station equipment, and energy storage systems.
The analysis of the arithmetic examples leads to the following conclusions:
1) Conflict between economic cost and carbon emissions:
Within the current power generation framework, there is a distinct conflict between the operational economic cost and carbon emissions of an ADN incorporating 5G communication base stations. 5G base station flexibility boosts renewable energy efficiency and utilization for major low-carbon gains.
2) Influence of response characteristics:
The response characteristics of 5G communication base stations are affected by multiple factors, including the number of active transceivers and the operating parameters of energy storage batteries. By optimizing base station equipment and the operational status of energy storage batteries while ensuring the quality of user communication services, the distribution of ADN power flows can be enhanced, network losses reduced, and the grid’s capacity for RES integration expanded.
3) Advantages of interval optimization method:
The interval optimization method accommodates the subjective preferences of decision-makers, offering a decision scheme that balances optimality and risk mitigation. This approach shows significant engineering value due to its flexibility and robustness in achieving a balanced and resilient optimization result.
6.2 Limitations and future directions
While this study presents a comprehensive method for optimizing the operation of ADNs with integrated 5G communication base stations, several limitations need to be addressed in future research:
-
Scalability and applicability: The model needs to be tested and validated on larger, more complex ADNs with diverse RES and 5G base station deployments to ensure scalability and applicability.
-
Dynamic load variability: Future work may explore more detailed modeling of dynamic load variability and its impact on ADN operation, incorporating real-time data and machine learning techniques for improved accuracy.
Funding
This work was supported by the State Grid Shanxi Electric Power Company Science and Technology Project (520533220006).
Conflicts of interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Data availability statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
- Fan M.T., Zhang Z.P., Su A.X., Su J. (2013) Enabling technologies for active distribution systems, Pro. CSEE 33, 22, 12–18+5. [Google Scholar]
- Xu X.L., Song Y.Q., Yao L.Z., Yan Z. (2018) Source-load-storage distributed coordinative optimization of ADN (Part I): Consensus based distributed coordination system modeling, Proc. CSEE 38, 10, 2841–2848+3135. [Google Scholar]
- Yong P., Zhang N., Ci S., Kang C.Q. (2021) 5G communication base stations participating in demand response: key technologies and prospects, Proc. CSEE 41, 16, 5540–5552. [Google Scholar]
- Fatma F.A., Israfil K., Mustafa Ş. (2023) Optimal scheduling of active electricity distribution network at feeder scale under possible conditions and considering operating cost, Electr. Eng. 105, 6, 3533–3547. [CrossRef] [Google Scholar]
- Rajeshwari S., ManMohan S.R., Varun B. (2022) A multi-objective optimization scheduling method based on the genetic algorithm in cloud computing, Int. J. Cloud Appl. Comput. 12, 1, 1–21. [Google Scholar]
- Wen J., Qu X., Lin S.Y., Ding L., Jiang L. (2022) An optimization method of active distribution network considering time variations in load and renewable distributed generation, Int. Trans. Electr. Energy Syst. 2022, 1–21. [CrossRef] [Google Scholar]
- Xu G., Zhang B., Yang L., Wang Y. (2021) Active and reactive power collaborative optimization for active distribution networks considering bi-directional V2G behavior, Sustainability 13, 6489. [CrossRef] [Google Scholar]
- Zhang J.M., Liu J., Liu D.F., Wang T. (2023) Coordinated scheme for expansion planning of transmission system with active distribution system flexibility provision, Energy Rep. 9, S1, 87–97. [CrossRef] [Google Scholar]
- Zhang J.R., Li Z.Y., Wang B.B. (2021) Within-day rolling optimal scheduling problem for active distribution networks by multi-objective evolutionary algorithm based on decomposition integrating with thought of simulated annealing, Energy 223, 120027. [CrossRef] [Google Scholar]
- Cui Q.S., Bai X.M., Zhu S.Z., Li N. (2016) ADN multi-objective planning considering collaborative optimization of RDG and GAEP, in: 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, NSW, Australia, 28 September–01 October, IEEE, pp. 1–7. [Google Scholar]
- Xu C.B., Yang X.D., Zhang Y.B. (2021) Stochastic operation optimization method for active distribution networks with soft open point considering risk management and control, Autom. Electr. Power Syst. 45, 11, 68–76. [Google Scholar]
- Li M., Furifu C., Ge C., Zheng Y.P. (2023) Distributed robust optimal dispatch for the microgrid considering output correlation between wind and photovoltaic, Energy Eng. 120, 8, 1775–1801. [CrossRef] [Google Scholar]
- Renga D., Hassan H., Meo M., Nuaymi L. (2018) Energy management and base station on/off switching in green mobile networks for offering ancillary services, IEEE Trans. Green Commun. Netw. 2, 3, 868–880. [CrossRef] [Google Scholar]
- Zeng B., Yang Y., Duan J., Zeng M., Ouyang S., Li C. (2015) Key issues and research prospects for demand-side response in alternate electrical power systems with renewable energy sources, Autom. Electr. Power Syst. 39, 17, 10–18. [Google Scholar]
- Liu Y., Wang Q., Zeng Q., Ye Y., Liu C., Xu L.X. (2021) Key technologies and prospects of energy consumption management for 5G network in background of energy internet, Autom. Electr. Power Syst. 45, 12, 174–183. [Google Scholar]
- Ali N., Ali M.J., Yazdan A. (2023) Injecting cognitive intelligence into beyond-5G networks: A MAC layer perspective, Comput. Electr. Eng. 108, 108717. [CrossRef] [Google Scholar]
- Fisusi A., Grace D., Mitchell P. (2017) Energy saving in a 5G separation architecture under different power model assumptions, Comput. Commun. 105, 89–104. [CrossRef] [Google Scholar]
- Guo W., Mao Y., Chen Y., Zhang X. (2022) Multi-objective optimization model of micro-grid access to 5G base station under the background of China’s carbon peak shaving and carbon neutrality targets, Front. Energy Res. 10, 1032993. [CrossRef] [MathSciNet] [Google Scholar]
- Vineet S., Mohammad K., Shivani B. (2022) Optimizing storage for energy conservation in tracking wireless sensor network objects, Comput. Syst. Sci. Eng. 45, 2, 1211–1231. [Google Scholar]
- Wang Q., Zhao X., Lv Z.T., Ma X.Y., Zhang R.T., Lin Y. (2020) Optimizing the ultra-dense 5G base stations in urban outdoor areas: coupling GIS and heuristic optimization, Sustain. Cities Soc. 63, 102445. [CrossRef] [Google Scholar]
- Dou A., Cui F.F., Kang X. (2023) Optimal scheduling for charging and discharging of electric vehicles based on deep reinforcement learning, Front. Energy Res. 11, 1273820. [CrossRef] [Google Scholar]
- Jiang C., Han X., Xie H.C. (2017) Theory and method of interval uncertainty optimal design, Science Press, Beijing. [Google Scholar]
- Dolatabadi S.H., Ghorbanian M., Siano P., Hatziargyriou N.D. (2020) An enhanced IEEE 33 bus benchmark test system for distribution system studies, IEEE Trans. Power Syst. 36, 3, 2565–2572. [Google Scholar]
- Zeng B., Xu F.Q., Liu Y.X., Liu Y., Gong D.W. (2021) High-dimensional multiobjective optimization for multi-energy coupled system planning with consideration of economic, environmental and social factors, Proc. CSEE 36, 7, 1434–1445. [Google Scholar]
- Wang Y.W., Song M.H., Jia M.Y. (2023) Multi-objective distributionally robust optimization for hydrogen-involved total renewable energy CCHP planning under source-load uncertainties, Appl. Energy 342, 121212. [CrossRef] [Google Scholar]
- Lu Y., Dai Y., Ma W.Z., Wu X., Liu M.B., Lin S.J. (2019) Decentralized dynamic optimal power flow in distribution networks with distributed generation and energy storage devices, Power Syst. Technol. 43, 2, 434–442. [Google Scholar]
- Chen Q.H., He Y.H., Zeng Y.Z., Liu J., Li M.D. (2020) Application of TOPSIS method in the comprehensive evaluation of steam-air preheater on waste incineration boiler, Proc. CSEE 40, 4, 241–248+385. [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Equipment composition of 5G communication base stations. |
| In the text | |
 |
Fig. 2 Flowchart of solution procedures. |
| In the text | |
 |
Fig. 3 Modified IEEE 33-bus distribution network. |
| In the text | |
 |
Fig. 4 Curve of system communication load and power load. |
| In the text | |
 |
Fig. 5 Pareto Frontier set. |
| In the text | |
 |
Fig. 6 System power balance. |
| In the text | |
 |
Fig. 7 Wind power curtailment curve with and without interactions between 5G communication base stations and power grid. |
| In the text | |
 |
Fig. 8 Operation optimization results of each base station group. (a) Non-participation in DR operations (b) Participation in DR operations |
| In the text | |
 |
Fig. 9 Transceiver scheduling results with interaction of base stations. |
| In the text | |
 |
Fig. 10 Comparison results of different optimization schemes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




