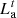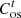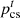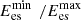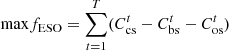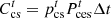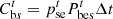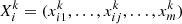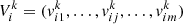| Issue |
Sci. Tech. Energ. Transition
Volume 80, 2025
Innovative Strategies and Technologies for Sustainable Renewable Energy and Low-Carbon Development
|
|
|---|---|---|
| Article Number | 44 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.2516/stet/2025024 | |
| Published online | 08 July 2025 | |
Regular Article
Low-carbon and economic optimization of a source-load-storage system based on Stackelberg game and chance constraints
1
State Grid Sichuan Economic and Technological Research Institute, Chengdu 610095, Sichuan Province, PR China
2
Sichuan New Electric Power System Research Institute, Chengdu 610095, Sichuan Province, PR China
* Corresponding author: ccntlc1@163.com
Received:
10
December
2024
Accepted:
12
May
2025
As energy demand grows and environmental pollution increases, low-carbon development has become a key focus in energy systems. To address the conflicting interests of the Source-Load-Storage System (SLSS), while also considering environmental benefits, this paper proposes an optimization model for the low-carbon economy of SLSS based on Stackelberg game theory and opportunity constraints. First, to ensure low carbon emissions and environmental protection, the carbon emissions of each entity in SLSS are constrained by a reward-penalty laddering carbon trading mechanism. Additionally, a demand response strategy is introduced on the user side, which accounts for both price and carbon compensation incentives. Next, considering the autonomy of the entities in SLSS, a decision-making model is developed based on the Stackelberg game. In this game-theoretic framework, the Power Management Operator acts as the leader, whereas the Power Generation Operator, Energy Storage Operator, and User serve as followers. This model also outlines the low-carbon interaction mechanisms among the various entities of SLSS. Finally, the model is solved using an improved particle swarm algorithm combined with the Gurobi optimization tool. Simulation results effectively validate the proposed model and method, showing that SLSS can rationally adjust its strategy within the low-carbon framework while balancing economic and environmental considerations.
Key words: Stackelberg game / Chance constraint programming / Source-load-storage / Low-carbon operation / The reward and penalty laddering-type carbon trading
© The Author(s), published by EDP Sciences, 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
SSLS: Source-load-storage system
PMO: Power management operator
PGO: Power generation operator
ISAC: Ice storage air conditioner
Parameters
γ : Random variable obeying a normal distribution
δp : Carbon emission allocations per unit of heat
Fc : Reward and punishment step-type carbon trading costs
Variables
DGPMO : Unpaid carbon subsidies for power purchased from the external grid
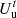 :
Indicator of user satisfaction
:
Indicator of user satisfaction
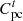 :
Penalty cost to be borne by cooling interruptions
:
Penalty cost to be borne by cooling interruptions
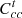 :
PMO carbon trading costs for purchasing electricity from the grid
:
PMO carbon trading costs for purchasing electricity from the grid
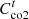 :
User carbon offset coefficients
:
User carbon offset coefficients
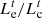 :
Customer-side electric and cold load
:
Customer-side electric and cold load
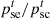 :
Price of electricity and energy sold by the PMO
:
Price of electricity and energy sold by the PMO
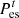 :
Power of electricity sold by the PMO to the PSO
:
Power of electricity sold by the PMO to the PSO
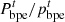 :
Power of electricity and the price of electricity purchased by the PMO from the PGO
:
Power of electricity and the price of electricity purchased by the PMO from the PGO
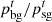 :
Price of electricity purchased and sold by the PMO from the grid
:
Price of electricity purchased and sold by the PMO from the grid
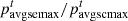 :
Average prices of electricity and cold energy sold
:
Average prices of electricity and cold energy sold
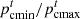 :
Minimum and Maximum prices of cold energy
:
Minimum and Maximum prices of cold energy
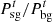 :
PMO sold and purchased electric power
:
PMO sold and purchased electric power
ηbes/ηces : Charging and discharging efficiencies of the storage device
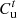 :
Price function paid for purchased energy
:
Price function paid for purchased energy
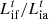 :
Fixed load and adjustable load
:
Fixed load and adjustable load
1 Introduction
As energy demand increases and the frequency of extreme weather events increases, low-carbon and cleaner energy have become the mainstream direction of energy development [1]. Low-carbon clean energy not only supports long-term economic growth but also reduces the use of fossil fuels [2], effectively mitigating global warming [3, 4]. In recent years, the synergistic planning technology of Integrated Energy System (IES) with smart grid as the core hub, combining power grid, natural gas network, and heat transmission network, has become a new research hotspot and cutting-edge [5]. IES can coordinate and optimise the production, transmission, and consumption of multiple energy sources, greatly reducing waste and achieving the goal of improving overall energy efficiency and renewable energy consumption [6], and effectively reducing carbon emissions [7], making IES an important example of an energy supply system.
IES focuses on the synergistic optimisation of the cogeneration system, and then gradually expands and enriches the system, involving the synergistic complementarity of multiple energy subsystems, such as electricity, heat, cold, and natural gas, in terms of their production, transmission, storage, use, and conversion [8]. Integration of multiple energy sources and collaborative scheduling of IES to achieve security, economy, and flexibility of multiple energy supplies require optimisation of IES operation. In recent years, the power demand side response theory has been gradually extended to the integrated demand response theory in the energy Internet. In Reference [9], considering the wind power prediction error and the demand response characteristics, a multi-timescale optimal scheduling model of the power system is established to construct the demand response with the minimum cost of the grid operation and to improve the system’s ability to consume wind power. Reference [10] proposed a two-level scheduling optimization model for virtual power plants, which can smooth out the fluctuation of new energy access and promote the grid integration of new energy sources such as wind and light. Reference [11] proposed an optimal scheduling model based on Combined Cooling, Heating and Power (CCHP) and carbon capture device, taking into account the demand response of cooling, heating, and power loads and the stepped carbon trading mechanism. Reference [12], a multilevel distributed demand response model for a multi-campus integrated energy system is proposed using a particle swarm optimisation algorithm and mixed integer linear programming. Reference [13], a demand response model for energy users is developed to solve the congestion cost sharing problem using a cooperative game pricing approach. A multi-objective optimisation model for the thermoelectricity of an IES based on a multi-objective bi-dynamic genetic algorithm was constructed in [14]. Reference [15] introduced a comprehensive three-stage optimisation methodology of “Day-ahead-Day-intra rolling-Real-time peak regulation and frequency modulation”, which systematically optimises the output schedule of the system at different stages. The above studies are all methods to optimise the operation of IES, but they do not take into account the conflict of interest between multiple subjects within IES, and how IES can ensure the benefits of each subject while operating efficiently is a problem that still needs to be solved.
The IES consists of multiple subjects of interest, and the operation of the IES relies on the coordination and coordination between multiple subjects [16]. Game theory, as a concept in the field of economics, is widely used in a variety of fields and is now well integrated into power markets, power system scheduling, power system control [17], etc. Game theory is an important method for resolving conflicts between subjects with different interests and is used to describe the interactive behaviour of different subjects. Reference [18] referred to the operating model of the sharing economy and constructs a Stackelberg model with IES operators as leaders and producers and consumers as followers. Reference [19] constructed a multi-leader multi-follower Stackelberg model for analysing the multi-energy trading problem in IES. Reference [20] investigated optimisation models incorporating shared energy storage systems, microgrid operators, electric vehicle power stations, and multiple users on aggregation, integrating a two-way Stackelberg-Nash game optimisation model. Reference [21] focused on the interaction of multiple energy types in the IES to achieve stable operation, economic, and environmental improvements for each subject and the region as a whole. Reference [22] proposed a joint planning methodology for integrated multi-park energy systems based on cooperative games for efficient energy use and economic efficiency. The above study investigated the interaction of interests of multiple subjects in IES through a game but failed to fully consider the interaction between the supply and demand sides, and failed to reflect the role of the energy management side for optimal scheduling. Therefore, it is necessary to make a more detailed division of each stakeholder in IES and do more in-depth research on the energy coupling and co-optimisation of multi-stakeholders.
IES is equally effective in achieving peak carbon and carbon-neutral targets. Reference [23] constructed a two-tier optimal scheduling framework for integrated community energy participation to reduce carbon emissions and effectively balance total operating costs. Reference [24] proposed an optimal scheduling method for the two-way flow of electricity and carbon in transmission and distribution networks, taking into account seasonal carbon trading. Reference [25] analysed carbon source loading uncertainty, modelling uncertain parameters using uncertainty sets. Reference [26] proposed a carbon-integrated energy pricing strategy based on non-cooperative game theory, modelling carbon emission flows. The reward-punishment ladder carbon trading model effectively achieves the goals of carbon conservation and emission reduction through a clear mechanism of rewards and penalties. Reference [27] integrates a laddered reward-punishment system and introduces a probabilistic, data-driven approach to optimize operations. Reference [28] applies the reward-punishment ladder carbon trading mechanism to develop an operational strategy for energy hubs, avoiding the reliance on fixed carbon prices and considering the incentive potential of carbon trading. However, most current studies overlook the impact of carbon emissions on system pollution. This study, therefore, takes into account not only the environmental impact of carbon emissions but also their effect on the system in a multi-interest game scenario.
Aiming at the above problems, this paper proposes a research method of source-load-storage multi-body two-layer scheduling optimisation considering the Stackelberg game. The contributions of this paper are as follows:
-
This paper introduces a reward-and-penalty ladder-based carbon trading mechanism and develops a corresponding cost calculation model. By comprehensively accounting for the carbon emissions of each entity, it further proposes a demand response strategy that leverages dual incentive electricity pricing and carbon compensation. This approach enhances the green regulatory role of all stakeholders and promotes the coordinated development of both power and carbon markets.
-
Utilizing Stackelberg game theory, the Power Management Operator (PMO) acts as the leader, while the Power Generation Operator (PGO), Energy Storage Operator (ESO), and users serve as followers. By guiding participants through appropriate price signals, the model achieves coordinated and optimised dispatch of multiple energy sources across various stakeholders, while accounting for both economic and environmental benefits.
2 Source-load-storage multi-body game and carbon trading mechanism
2.1 Source-load-storage structure
The structure of SLSS with multiple forms of energy is shown in Figure 1.
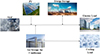 |
Fig. 1 The structure of SLSS. |
In Figure 1, the SLSS structure contains three forms of energy: cooling, electricity, and gas. Among them, SLSS can purchase electricity externally to meet the electricity demand. Photovoltaic is an energy supply device, Ice Storage Air Conditioner (ISAC) is an energy conversion device.
2.2 Carbon price mechanism with laddered rewards and penalties
The reward and penalty laddering-type carbon trading provides economic incentives for SLSS to make a profit from the sale of excess carbon allowances [29], which helps to reduce the cost of carbon trading, and analyses the parameters of the carbon trading price, where an increase in the price of carbon trading leads to an increase in the proportion of low-carbon energy sources and a reduction in carbon emissions in SLSS, keeping the system economical and environmentally friendly. The initial allocation of carbon credits in this paper is for purchased electricity. Purchased power generates carbon trading costs that are part of the PMO.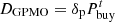 (1)
(1)
where DGPMO and δp are unpaid carbon subsidies for power purchased from the external grid and carbon emission allocations per unit of heat, respectively.
To stimulate the main motivation of the main body to reduce carbon emissions, the construction of reward and punishment step-type carbon trading costs Fc. Give incentives when the PMO carbon emission Dr is lower than the free carbon credit Df, and conversely, require the purchase of shortfalls.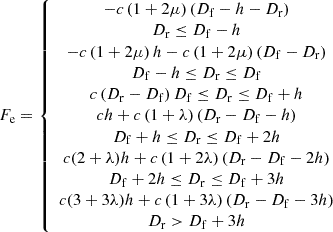 (2)
(2)
where μ and λ represent incentive and penalty coefficients, respectively. c is a carbon trading price. n is the length of the carbon emission interval.
2.3 Demand response strategy considering dual incentives
The demand response strategy that considers both price and carbon offset incentives is as follows:
-
When the load is in the valley, the PMO guides the customer to increase energy consumption. When the price of energy sales is in the valley, the customer adjusts the energy consumption strategy according to their satisfaction index. Based on the price incentive, the amount of change in electricity and cooling load increased by users in response to the price incentive will be converted into carbon compensation and rewarded to users to adjust the optimal adjustable load range of users.
-
When the load is in the ordinary period, the users only have less carbon compensation or almost no carbon compensation incentive, and the actual energy load of the users is close to the demand load.
-
When the load is in peak hours, PMO sets a higher energy sales price to guide users to actively reduce energy consumption, users adjust their energy consumption strategy according to their satisfaction indicators, and the amount of electricity and cooling load changes reduced in response to the price incentives are converted into carbon compensation incentives for users, stimulating users to adjust the optimal adjustable load range.
2.4 Source-load-storage multi-body game interaction model
The source-load-storage multi-subject game interaction model is shown in Figure 2.
 |
Fig. 2 The source-load-storage multi-subject game. |
The source-load-storage multi-subject Stackelberg game is shown in Figure 2. PMO is the leader, responsible for dominating and coordinating the SLSS energy market, and also assumes responsibility for balancing source-load-storage power. PMO can interact with the grid and is an operator with bi-directional energy flow. When the energy purchased by the PMO from the PGO cannot meet the customer’s load, the PMO must purchase additional power from the grid and bear the corresponding carbon emission cost. There are three followers: PGO, PMO, and the user. PGO is centred on PV generation as a function of maximising the benefits and minimising the costs of energy sales. As an energy storage party with dual attributes of power source and load, ESO can solve the problem of rapid fluctuation of new energy output, provide the necessary inertia support, and improve the flexibility of SLSS. PGO optimises its own charging and discharging power by maximising the benefit of price information. The abundance of resources on the user’s side is utilized to achieve the promotion of energy efficiency, maintain the source-load-storage balance, promote the consumption of renewable energy, protect against the risk of accidents, and guide SLSS-friendly interaction while mitigating investment.
3 Decision-making models for each subject of the game
3.1 PMO’s decision-making model
The PMO coordinates the various entities and coordinates the output of various equipment and the energy needs of the users. The PMO coordinates the various subjects, coordinates the output of the various devices and the energy demand of the consumers, and determines the price of purchased and sold electricity according to the time-of-use tariffs. The objective function is: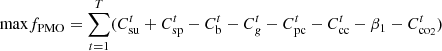 (3)
(3)
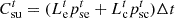 (4)
(4)
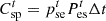 (5)
(5)
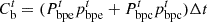 (6)
(6)
![$$ {C}_{\mathrm{g}}^t=\left[\begin{array}{c}\mathrm{max}\left({L}_{\mathrm{e}}^t-{P}_{\mathrm{bpe}}^t,\enspace 0\right){p}_{\mathrm{bg}}^t+\\ \mathrm{min}\left({L}_{\mathrm{e}}^t-{P}_{\mathrm{bpe}}^t,\enspace 0\right){p}_{\mathrm{sg}}^t\end{array}\right]\Delta t $$](/articles/stet/full_html/2025/01/stet20240453/stet20240453-eq25.gif) (7)
(7)
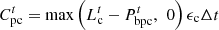 (8)
(8)
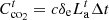 (9)where
(9)where 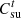 and
and 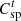 are the PMO’s revenue from energy sales to users and PSO, respectively;
are the PMO’s revenue from energy sales to users and PSO, respectively; 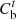 and
and 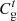 are the PMO’s interaction costs with PSO and grids, respectively;
are the PMO’s interaction costs with PSO and grids, respectively; 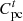 is the penalty cost to be borne by cooling interruptions;
is the penalty cost to be borne by cooling interruptions; 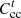 is the PMO’s carbon trading costs for purchasing electricity from the grid; β1 is the PMO’s weighting factor for assuming the users’ carbon offset coefficients; and
is the PMO’s carbon trading costs for purchasing electricity from the grid; β1 is the PMO’s weighting factor for assuming the users’ carbon offset coefficients; and 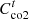 is the users’ carbon offset coefficients.
is the users’ carbon offset coefficients. 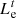 and
and 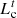 are the customer-side electric load and cold load, respectively;
are the customer-side electric load and cold load, respectively; 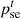 and
and 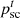 represent the price of electricity and cold energy sold by the PMO, respectively;
represent the price of electricity and cold energy sold by the PMO, respectively; 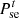 is the power of electricity sold by the PMO to the PSO;
is the power of electricity sold by the PMO to the PSO; 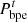 and
and 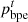 are the power of electricity and the price of electricity purchased by the PMO from the PGO, respectively;
are the power of electricity and the price of electricity purchased by the PMO from the PGO, respectively; 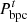 and
and 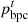 are the power of cold power and the price of cold purchased by the PMO from the PGO, respectively;
are the power of cold power and the price of cold purchased by the PMO from the PGO, respectively; 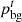 is the price of electricity purchased by the PMO from the grid; and
is the price of electricity purchased by the PMO from the grid; and 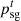 is the price of electricity sold by the PMO to the grid, ε1 is the penalty coefficient for the penalty for interruption of cooling supply;
is the price of electricity sold by the PMO to the grid, ε1 is the penalty coefficient for the penalty for interruption of cooling supply; 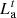 is the adjustable load of the user; T is the total time, which is 24 h.
is the adjustable load of the user; T is the total time, which is 24 h.
To ensure the synergistic operation of the subjects in the SLSS, the price of energy purchased and sold by the PMO should satisfy the following constraints.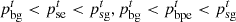 (10)
(10)
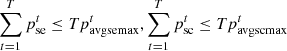 (11)
(11)
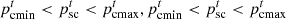 (12)
(12)
where 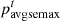 and
and 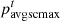 are the average prices of electricity and cold energy sold, respectively, and
are the average prices of electricity and cold energy sold, respectively, and 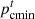 and
and 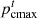 are the minimum and maximum prices of cold energy, respectively.
are the minimum and maximum prices of cold energy, respectively.
Meanwhile, the power constraints of the liaison line are as follows: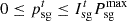 (13)
(13)
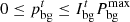 (14)
(14)
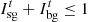 (15)
(15)
where 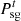 and
and 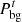 are the PMO sold and purchased electric power, respectively;
are the PMO sold and purchased electric power, respectively; 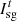 and
and 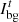 are both 0–1 variables, indicating the state of PMO selling or purchasing from the outsourced grid;
are both 0–1 variables, indicating the state of PMO selling or purchasing from the outsourced grid; 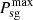 and
and 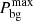 are the maximum value of PMO sold and purchased electric power, respectively.
are the maximum value of PMO sold and purchased electric power, respectively.
3.2 PGO’s decision-making model
After the PMO sets the energy price, the PGO makes its decisions based on the set price to maximise its profit with the following objective function: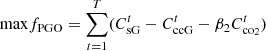 (16)where
(16)where 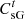 is the PGO’s interest in energy sales;
is the PGO’s interest in energy sales; 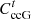 is the weighting factor for the PGO’s assumption of user carbon offsets; and β2 is the PGO’s carbon trading costs.
is the weighting factor for the PGO’s assumption of user carbon offsets; and β2 is the PGO’s carbon trading costs.
In the middle of time period t, the electric and cold power of PGO satisfies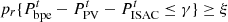 (17)
(17)
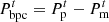 (18)where Pr{} is the probability of the event being established, γ is the random variable obeying a normal distribution, and ξ is the confidence level.
(18)where Pr{} is the probability of the event being established, γ is the random variable obeying a normal distribution, and ξ is the confidence level.
Energy constraints are described using opportunity constraints and converted to deterministic constraints by processing the opportunity constraints using a deterministic equivalence class approach: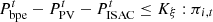 (19)
(19)
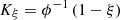 (20)where π
i,t
is the Lagrange multiplier corresponding to the inequality constraint; ϕ
−1 is the inverse function of the distribution function of the random variable ϕ. In the case where ϕ
−1 is multivalued, the maximum value is chosen:
(20)where π
i,t
is the Lagrange multiplier corresponding to the inequality constraint; ϕ
−1 is the inverse function of the distribution function of the random variable ϕ. In the case where ϕ
−1 is multivalued, the maximum value is chosen: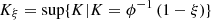 (21)where sup{} denotes the smallest upper bound of the set.
(21)where sup{} denotes the smallest upper bound of the set.
3.3 ESO’s decision-making model
where 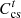 and
and 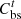 are the discharge revenue and charging cost of the ESO;
are the discharge revenue and charging cost of the ESO; 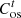 is the O&M cost of the ESO; and
is the O&M cost of the ESO; and 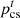 is the electricity sales price of the ESO.
is the electricity sales price of the ESO.
The energy storage state of the ESO should satisfy the following constraints: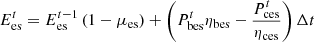 (25)
(25)
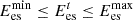 (26)
(26)
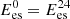 (27)where ηbes and ηces are the charging and discharging efficiencies of the storage device;
(27)where ηbes and ηces are the charging and discharging efficiencies of the storage device; 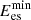 and
and 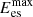 are the minimum and maximum values; and μes is the energy loss rate of the storage device itself.
are the minimum and maximum values; and μes is the energy loss rate of the storage device itself.
3.4 User’s decision-making model
The user’s optimisation objective function is: 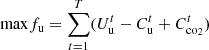 (28)
(28)
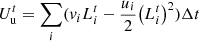 (29)
(29)
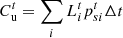 (30)where
(30)where 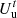 is an indicator of user satisfaction, and
is an indicator of user satisfaction, and 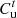 is the price function paid for purchased energy. In this paper, a quadratic function is used to characterise
is the price function paid for purchased energy. In this paper, a quadratic function is used to characterise 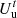 . Where i ∈ {e, c}, ν
i
and u
i
are preference coefficients for the consumption of electrical and cooling energy by users.
. Where i ∈ {e, c}, ν
i
and u
i
are preference coefficients for the consumption of electrical and cooling energy by users.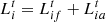 (31)
(31)
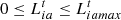 (32)
(32)
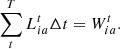 (33)
(33)
The user’s 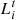 load consists of two parts: fixed load
load consists of two parts: fixed load 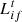 and adjustable load
and adjustable load 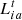 .
. 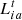 can be adjusted according to the price and is related to the customer’s satisfaction with the energy consumption.
can be adjusted according to the price and is related to the customer’s satisfaction with the energy consumption. 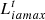 is the maximum value in time period t and
is the maximum value in time period t and 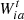 is the total transferable load of electric and cooling loads in time period t.
is the total transferable load of electric and cooling loads in time period t.
4 Multi-subject game interaction analysis
4.1 The equilibrium of the Stackelberg game for ESO
Multi-subject Stackelberg game is used to describe the decision-making process of PMO, PGO, ESO, and users in pursuit of the optimality of their own goals. In gaming, the leader is the PMO, and the followers are the PGO, ESO, and the user. The Stackelberg game model can be expressed as follows: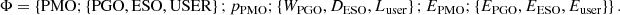
The model contains participants, strategies, and utilities. The participants include the leader PMO and the followers PGO, ESO, and users; the strategies include the PMO’s purchase and sale of energy price PPMO, the output power of the energy supply equipment in the PGO WPGO, the charging and discharging power in the ESO DESO, and the users’ adjustable electricity and cooling loads Luser; and the utility of each participant is the objective function of the aforementioned subjects of interest.
In the process of the game, when no subject of interest can unilaterally change the strategy of the equilibrium solution to gain, it means that the game reaches the Stackelberg equilibrium, i.e., it satisfies the conditions of the following equation, then (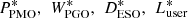 ) is the equilibrium of the Stackelberg game.
) is the equilibrium of the Stackelberg game.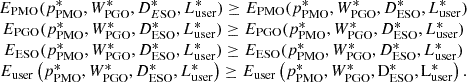
4.2 Game-solving method
The improved particle swarm algorithm, combined with the Gurobi solver, is used to solve the established multi-subject master-slave game model.
The algorithmic flow of PSO is shown in Figure 3.
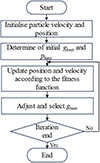 |
Fig. 3 The flow of the PSO algorithm. |
The upper layer algorithm is shown in Figure 3. The steps are as follows:
-
Initialise particle velocity and position.
-
Calculate and store the target vector value of the particle.
-
Determine the initial gbest and pbest of the particle.
-
Update particle positions and velocities according to the fitness function.
-
Adjust pbest and select gbest for particles.
The traditional PSO algorithm is prone to local optimal solutions and has poor diversity. Therefore, it is necessary to improve it to enhance the global search capability and improve the convergence. Before improving it, the following assumptions are made:
-
The search space is an n-dimensional space;
-
The number of particles is N. When the number of iterations is k, the position and velocity information of the ith particle are respectively:
where i denotes the ith particle and there are i ∈ [0, N]; j denotes the space dimension and there is j ∈ [0, n]; 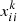 denotes the j-dimensional position component of particle i at iteration number k; superscript k and subscript ii denote the j-dimensional velocity component of particle i at iteration number k.
denotes the j-dimensional position component of particle i at iteration number k; superscript k and subscript ii denote the j-dimensional velocity component of particle i at iteration number k.
Further, the optimal solution Pbest encountered in the particle neighbourhood domain and the optimal solution gbest encountered by the current population are denoted as: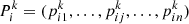 (36)
(36)
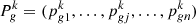 (37)where
(37)where 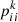 and
and 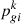 are the j-dimensional optimal position component and the global optimal component of particle i at the kth iteration, respectively.
are the j-dimensional optimal position component and the global optimal component of particle i at the kth iteration, respectively.
The position and velocity information of the i particle is computed: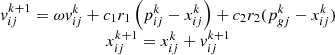 (38)where
(38)where 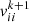 denotes the j-dimensional velocity component of particle i when the number of iterations is k + 1; c1, c2 are the learning factors representing the experience of the population and the degree to which the particles are influenced by the experience, respectively, and there are c1 > 0, c2 > 0; r1, r2 denote the uniformly distributed random numbers with the distribution range of [0, 1]; ω denotes the inertia weights, which mean that there is a change in the speed of an individual concerning the original speed difference that exists.
denotes the j-dimensional velocity component of particle i when the number of iterations is k + 1; c1, c2 are the learning factors representing the experience of the population and the degree to which the particles are influenced by the experience, respectively, and there are c1 > 0, c2 > 0; r1, r2 denote the uniformly distributed random numbers with the distribution range of [0, 1]; ω denotes the inertia weights, which mean that there is a change in the speed of an individual concerning the original speed difference that exists.
In general, the search direction of the particles is random and does not have any particular restriction, which brings unnecessary computational cost to the optimisation process. To keep the particle’s position and velocity within an acceptable range during its search, its search velocity is limited, i.e., the range of values of velocity [Vmin, Vmax], and the velocity is taken to be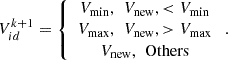 (39)
(39)
From this, the particle positions can be deduced: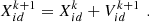 (40)
(40)
The inertia weights ω update formula in the PSO algorithm was modified: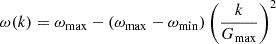 (41)where ωmax is the initial value of inertia weights; ωmin is the inertia weight of the last iteration; Gmax is the number of iterations.
(41)where ωmax is the initial value of inertia weights; ωmin is the inertia weight of the last iteration; Gmax is the number of iterations.
The lower layer algorithm uses Gurobi as a solution tool to calculate the optimal output of the PGO’s energy supply device, the optimal charging and discharging power of the ESO’s energy storage device, and the user’s adjustable loads for cooling and electricity, and sends the optimization results to the upper layer leader.
5 Case study
The simulation in this paper is based on MATLAB 2021a. Take a certain SLSS as an example. The customer demand load and PV forecast data for the region are shown in Figure 4.
 |
Fig. 4 The load and PV forecast curve. |
Let the user’s adjustable electric load be 20% of the total demanded electric load, and the adjustable cooling load be 10% of the total demanded cooling load. The constant coefficients of user preference for electricity and cooling energy ve, ue, vc, uc, are 1.6 0.0012 1.4 0.001, respectively.
It is assumed that the user’s adjustable electric load accounts for 20% of the total demanded electric load, and the adjustable heat and cooling load accounts for 10% of the total demanded heat and cooling load.
5.1 Stackelberg game equilibrium
The PMO pricing strategy after the game equilibrium is shown in Figure 5.
 |
Fig. 5 Iteration curve. |
Figure 6a shows the PMO’s tariff strategy and Figure 6b shows the PMO’s cold tariff strategy. As shown in Figure 6a, to prioritise the consumption of new energy in the system, the PMO adopts an electricity pricing strategy that always sets its pricing within the external grid pricing range, providing more competitive prices for both energy suppliers and energy users. At the same time, the PMO’s sales price is aligned with the external grid’s time-of-day tariffs, while the purchase price matches the trend of actual customer loads, providing incentives for customers to actively purchase power and support PGO generation. Similarly, as in Figure 6b, the pricing strategy of the cooling price is also similar to the logic of the electricity price, and the purchase price of cooling is consistent with the trend of the actual cooling load of the customers.
 |
Fig. 6 Energy price curve. a) PMO’s tariff strategy; b) PMO’s cold tariff strategy. |
The results of the Stackelberg game optimisation for electricity energy scheduling are shown in Figure 7.
 |
Fig. 7 Energy optimisation result. a) Electricity energy optimisation result; b) Cooling energy optimisation result. |
Considering environmental friendliness, PMO prioritises the consumption of PV, firstly, for the 23:00–07:00 time period, when the electrical and cooling loads are low and the tariffs are in the valley, the excess is stored by the ESO’s batteries by the PGO to make a profit. The cooling load demand is low and is mainly provided by ISAC. Secondly, during 08:00–10:00 and 14:00–17:00, with the gradual increase of electric and cooling loads, the PV output of the PGO is fully consumed, and the portion of the load demand that cannot be met by the PGO is supplemented by the PMO through purchased power. Cold loads are supplied by ISAC, which consumes less electricity, through air-conditioning mode and ice-melting refrigeration at the same time. Finally, during the 11:00–13:00 and 18:00–23:00 hours, when the electrical loads are at their peaks, the shortfalls in the consumers’ electricity are supplemented by battery discharges and purchased electricity from PMO.
To better illustrate the economic and environmental benefits of optimal scheduling in a multi-agent game framework, considering integrated demand response and the reward-penalty laddering carbon trading mechanism, we design the following strategies for comparison with those in this paper:
-
Consider the PMO, PGO, ESO, and users without integrated demand response.
-
Consider the PMO, PGO, ESO, and users with integrated demand response.
-
Consider the PMO, PGO, ESO, and users with integrated demand response and the conventional carbon trading mechanism.
The comparison results are presented in Tables 1 and 2.
Each subject profit.
Each subject carbon emission.
As shown in Tables 1 and 2, compared to Strategies 1 and 2, the benefits for the PGO and users in Strategy 2 increase by 6.8% and 8.6%, respectively, and carbon emissions are reduced by 7.4% compared to Strategy 1. This improvement is due to the consideration of integrated demand response in Strategy 2, which effectively smoothes the peak-to-valley difference in customer load and reduces carbon emissions by lowering the cost of purchased energy.
When comparing Strategy 2 with Strategy 3, the profit for the PGO and users in Strategy 3 increases by 6.1% and 13.4%, respectively, compared to Strategy 2. However, the PMO’s profit decreases by 2.8% in Strategy 3, as the PMO bears the carbon trading cost of purchased power. Meanwhile, the PGO increases its output, which reduces the PMO’s cost of purchasing power from external sources and lowers carbon emissions.
Compared to the strategy in this paper, the profit and total system emissions for the PGO in this paper’s strategy increased by 7.4% and decreased by 3%, respectively, compared to Strategy 3. This is because the PGO is rewarded for producing fewer carbon emissions than the required emissions allocation. As a result of the increased output from the PGO, the PMO reduces power purchases from external sources, further lowering carbon emissions.
Overall, the comparison demonstrates that the model used in this paper can more effectively enhance emission reduction.
6 Limitations of the study
Two aspects of our study require some caution when interpreting the results. First, an unstable energy supply is also a major reason for the difficulty of reducing carbon emissions. Especially, wind power and photovoltaic as representatives of clean energy; their output has a strong stochastic nature, which is greatly affected by environmental factors, and the output characteristics of new energy power plants in different regions are different, so how to accurately predict the output of new energy is very important. The prediction model constructed in this study performs well in specific scenarios, but its generalization ability needs to be improved when facing new energy power plants in different regions. Meanwhile, the current model can fit the new energy output well under most of the regular weather conditions, but the prediction error is still large for the drastic fluctuations caused by extreme weather.
Second, this study constructs a carbon trading cost calculation model with a ladder mechanism of rewards and penalties in the hope of truly reflecting the carbon cost pressure faced by enterprises at different emission levels. Price fluctuations in the actual carbon market are affected by a variety of factors such as supply and demand, trading strategies, and market manipulation, etc. This model treats the carbon price as a linear or segmented function, which makes it difficult to reflect its true market fluctuation characteristics and affects the accuracy of cost assessment. At the same time, the model defaults that enterprises are completely rational in carbon trading and will flexibly adjust their emission and trading strategies according to the cost changes, however, in reality, the behavior of enterprises is often affected by irrational factors such as organizational inertia, information asymmetry, and risk aversion, which leads to the deviation between the model and the actual behaviors.
7 Conclusion
This paper develops a Stackelberg-based low-carbon economic optimization model for SLSS, with PMO as the leader and PGO, ESO, and users as followers. The model integrates a reward-penalty ladder-type carbon trading mechanism, a demand response strategy, and opportunity constraints. It guides each entity’s contribution through a price signaling system, optimizes individual energy usage strategies, and achieves coordinated optimization of SLSS. The reward-penalty ladder-type carbon trading mechanism is introduced to analyze each stakeholder’s decision-making behavior under carbon constraints, while opportunity constraints are employed to characterize export uncertainty, thereby reflecting the low-carbon regulatory capabilities of each participant. Simulation results demonstrate that, with the implementation of the proposed carbon trading mechanism and demand response strategy, system carbon emissions and the peak-valley difference of consumer electricity loads are reduced by 3% and 7.4%, respectively. These findings indicate that the proposed approach can effectively enhance the overall benefits for multiple stakeholders while ensuring the environmental efficiency of SLSS.
Funding
This work was supported by the Science and Technology Project of State Grid Sichuan Electric Power Company [Grant No. 521996240004].
References
- Wang C., Lv C., Li P., Song G., Li S., Xu X., Wu J. (2018) Modeling and optimal operation of community integrated energy systems: a case study from China, Appl. Energy 230, 1242–1254. [CrossRef] [Google Scholar]
- Van Tran H. (2024) Asymmetric role of economic growth, globalization, green growth, and renewable energy in achieving environmental sustainability, Emerg. Sci. J. 8, 449–462. [CrossRef] [Google Scholar]
- Cruz-Pérez N., Rodríguez Alcántara J.S., Koronaiou V.L., Jančula A., Rodríguez-Martín J., García Gil A., Fontes J.C., Santamarta J.C. (2024) SWOT analysis of the benefits of hydropower energy in four archipelagos, Civ. Eng. J. 10, 2370–2383. [CrossRef] [Google Scholar]
- Koestoer R.H., Ligayanti T., Kartohardjono S., Susanto H. (2024) Down-streaming small-scale green ammonia to nitrogen-phosphorus fertilizer tablets for rural communities, Emerg. Sci. J. 8, 625–643. [CrossRef] [Google Scholar]
- Good N. (2019) Using behavioural economic theory in modelling of demand response, Appl. Energy 239, 107–116. [CrossRef] [Google Scholar]
- Liu X. (2023) Bi-layer game method for scheduling of virtual power plant with multiple regional integrated energy systems, Int. J. Electr. Power Energy Syst. 149, 109063. [Google Scholar]
- Chen X., Yang L., Dong W., Yang Q. (2024) Net-zero carbon emission oriented bi-level optimal capacity planning of integrated energy system considering carbon capture and hydrogen facilities, Renew. Energ 237, 121624. [Google Scholar]
- Wang Y., Ma Y., Song F., Ma Y., Qi C., Huang F., Xing J., Zhang F. (2024) Economic and efficient multi-objective operation optimization of integrated energy system considering electro-thermal demand response, Energy 205, 118022. [Google Scholar]
- Li C.Y., Chen X., Zhang P., Zhang Q. (2018) Multi-time-scale demand response dispatch considering wind power forecast error, Power Syst. Technol. 42, 487–494. [Google Scholar]
- Zhang L.H., He H., Li Q.Y., Jiao Y., Tan Z.F. (2017) A bi-level stochastic scheduling optimization model for virtual power plant connecting with wind-photovoltaic-gas-energy storage system with considering uncertainty and demand response, Appl. Energy 171, 184–199. [Google Scholar]
- Yang P., Jiang H., Liu C., Kang C., Wang C. (2023) Coordinated optimization scheduling operation of integrated energy system considering demand response and carbon trading mechanism, Int. J. Electr. Power Energy Syst. 147, 108902. [Google Scholar]
- Zhang G., Niu Y., Xie T., Zhang K. (2023) Multi-level distributed demand response study for a multi-park integrated energy system, Energy Rep. 9, 2676–2689. [CrossRef] [Google Scholar]
- Yang J., Yang M., Ma K., Dou C., Ma T. (2024) Distributed optimization of integrated energy system considering demand response and congestion cost allocation mechanism, Int. J. Electr. Power Energy Syst. 157, 109865. [Google Scholar]
- Luo Y., Yang S., Niu C., Hua Z., Zhang S. (2024) A multi-objective dual dynamic genetic algorithm-based approach for thermoelectric optimization of integrated urban energy systems, Energy Rep. 12, 4175–4183. [CrossRef] [Google Scholar]
- Qian J., Guo Y., Wu D., Liu A., Han Z., Liu Z., Zhang S., Yang X. (2024) Research on multi-time scale optimization of integrated energy system based on multiple energy storage, J. Energy Storage 102, 113892. [Google Scholar]
- MacCarty N.A., Bryden K.M. (2016) An integrated systems model for energy services in rural developing communities, Energy 113, 536–557. [CrossRef] [Google Scholar]
- He J., Li Y., Li H., Tong H., Yuan Z., Yang X., Huang W. (2020) Application of game theory in integrated energy system systems: a review, IEEE Access 8, 93380–93397. [CrossRef] [Google Scholar]
- Peng Q., Wang X., Kuang Y., Wang Y., Zhao H., Wang Z., Lyu J. (2021) Hybrid energy sharing mechanism for integrated energy systems based on the Stackelberg game, CSEE J. Power Energy Syst. 7, 911–921. [Google Scholar]
- Wei F., Jing Z.X., Wu P.Z., Wu Q.H. (2017) A Stackelberg game approach for multiple energies trading in integrated energy systems, Appl. Energy 200, 315–329. [CrossRef] [Google Scholar]
- Wang Y., Jin Z., Liang J., Li Z., Dinavahi V., Liang J. (2024) Low-carbon optimal scheduling of park-integrated energy system based on bidirectional Stackelberg-Nash game theory, Energy 305, 132342. [CrossRef] [Google Scholar]
- Fu Y., Sun Q., Wennersten R., Pang X., Liu W. (2024) Interactive scheduling optimization of regional multi-agent integrated energy systems considering uncertainties based on game theory, J. Clean. Prod. 449, 141697. [Google Scholar]
- Chen C., Liu C., Ma L., Chen T., Wei Y., Qiu W., Lin Z., Li Z. (2023) Cooperative-game-based joint planning and cost allocation for multiple park-level integrated energy systems with shared energy storage, J. Energy Storage 73, 108861. [Google Scholar]
- Liang N., He X., Tan J., Pan Z., Zheng F. (2023) Stackelberg game-based optimal scheduling for multi-community integrated energy systems considering energy interaction and carbon trading, Int. J. Electr. Power Energy Syst. 153, 109360. [Google Scholar]
- Huo S., Li Q., Pu Y., Xie S., Chen W. (2024) Low carbon dispatch method for hydrogen-containing integrated energy system considering seasonal carbon trading and energy sharing mechanism, Energy 308, 132794. [CrossRef] [Google Scholar]
- Chu X., Fu L., Liu Q., Yu S. (2024) Optimal allocation method of oxygen enriched combustion-carbon capture low-carbon integrated energy system considering uncertainty of carbon-source-load, Int. J. Electr. Power Energy Syst. 162, 110220. [Google Scholar]
- Yang J., Zhao B., Ma K., Zhong J., Xu W. (2024) A carbon integrated energy pricing strategy based on non-cooperative game for energy hub in seaport energy system, Energy 309, 133009. [CrossRef] [Google Scholar]
- Gao M., Xiang L., Zhu S., Lin Q. (2024) Scenario probabilistic data-driven two-stage robust optimal operation strategy for regional integrated energy systems considering ladder-type carbon trading, Renew. Energy 237, 121722. [Google Scholar]
- Wang H., Zhao A., Khan M.Q., Sun W. (2024) Optimal operation of energy hub considering reward-punishment ladder carbon trading and electrothermal demand coupling, Energy 286, 129571. [CrossRef] [Google Scholar]
- Luo Y., Hao H., Yang D., Zhou B. (2024) Multi-objective optimization of integrated energy systems considering ladder-type carbon emission trading and refined load demand response, J. Mod. Power Syst. Clean Enegy 12, 828–839. [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The structure of SLSS. |
| In the text | |
 |
Fig. 2 The source-load-storage multi-subject game. |
| In the text | |
 |
Fig. 3 The flow of the PSO algorithm. |
| In the text | |
 |
Fig. 4 The load and PV forecast curve. |
| In the text | |
 |
Fig. 5 Iteration curve. |
| In the text | |
 |
Fig. 6 Energy price curve. a) PMO’s tariff strategy; b) PMO’s cold tariff strategy. |
| In the text | |
 |
Fig. 7 Energy optimisation result. a) Electricity energy optimisation result; b) Cooling energy optimisation result. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.