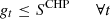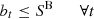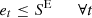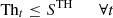| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Emerging Advances in Hybrid Renewable Energy Systems and Integration
|
|
|---|---|---|
| Article Number | 29 | |
| Number of page(s) | 15 | |
| DOI | https://doi.org/10.2516/stet/2024025 | |
| Published online | 07 May 2024 | |
Regular Article
Efficient economic energy scheduling in smart cities using distributed energy resources
1
Department of Computer Science, COMSATS University Islamabad, Islamabad 44500, Pakistan
2
Department of Engineering, University of Palermo, 90133 Palermo, PA, Italy
3
Faculty of Computing, Engineering and the Built Environment, Ulster University, BT37 0QB Newtownabbey, UK
4
Information & Computer Science Department King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Saudi Arabia
5
Faculty of Computing and Information Technology, Sohar University, Sohar 311, Oman
6
National University of Sciences and Technology (NUST), Islamabad 44500, Pakistan
* Corresponding author: hasan.alikhattak@acm.org
Received:
1
February
2024
Accepted:
3
April
2024
Machine learning provides a powerful mechanism to enhance the capabilities of the next generation of smart cities. Whether healthcare monitoring, building automation, energy management, or traffic management, use cases of capability enhancement using machine learning have been significant in recent years. This paper proposes a modeling approach for scheduling energy consumption within smart homes based on a non-dominated sorting genetic algorithm (NSGA). Distributed energy management plays a significant role in reducing energy consumption and carbon emissions as compared to centralized energy generation. Multiple energy consumers can schedule energy-consuming household tasks using home energy management systems in coordination to reduce economic costs and greenhouse gas emissions. In this work, such a home energy management system is used to collect energy price data from the electricity company via an embedded device-enabled smart meter and schedule energy consumption tasks based on this data. We schedule daily power consumption tasks using a multiobjective optimization method that considers environmental and economic sustainability. Two conflicting objectives are minimizing daily energy costs and reducing carbon dioxide emissions. Based on electricity tariffs, CO2 intensity, and the window of time during which electricity is consumed, energy consumption tasks involving distributed energy resources (DERs) and electricity consumption are scheduled. The proposed model is implemented in a model smart building consisting of 30 homes under 3 pricing schemes. The energy demand is spread out across a 24-hour period for points A2–A4 under CPP-PDC, which produces a more flattened curve than point A1. There are competing goals between electricity costs and carbon footprints at points B2–B4 under the CPP-PDC, where electricity demand is set between 20:00 and 0:00. Power grids’ peak energy demand is comparatively low when scheduling under CPP-PDC for points A5 and B5. Reducing carbon emissions, CPP-PDC reduces the maximum demand for electricity from the grid and the overall demand above the predetermined level. The maximum power demand from the grid is minimized for points A5 and B5, reducing up to 22% compared to A2. The proposed method minimizes both energy costs as well as CO2 emissions. A Pareto curve illustrates the trade-off between cost and CO2 emissions.
Key words: Micro grid / Demand response / Multiobjective optimization / Home energy management / Distributed energy resources / Non-dominated sorting genetic algorithm
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Power networks are considered the most comprehensive and complex energy systems ever made, and it is crucial to balance energy demand and supply continuously throughout the system to maintain a stable power supply [1, 2]. Due to increased electricity demand in recent years, conventional energy sources do not meet the increasing energy requirements [3]. Integration of renewable energy sources (RESs) alongside energy management systems (EMSs) and modern technology into the conventional grid may lower the excessive energy demand [4]. When connected with the loads, various RESs like photovoltaic (PV) and wind energy (WE) units make an MG. Additionally, this MG is converted into a smart microgrid (SMG) when incorporated with intelligent schemes [5] and mitigates various complex issues encountered in conventional electrical networks [6]. MGs are a satisfactory solution to meet consumers’ ever-increasing energy demands. MGs offered an emerging power system and shifted the traditional centralized power system towards a more localized and distributed generation system, particularly in urban areas. SMG enables two-way communication between utilities and end-users.
Developing effective demand response (DR) can be challenging, including integrating RESs, monitoring, intelligent sensors, and advanced control [7, 8]. DSM is a modern technology used for planning, directing, and coordinating utilities’ actions and behaviors [9, 10]. Using DSM combined with incentives, electricity rates, and punishments, energy consumption can be significantly increased. The power supply operation of a specific load is manually interrupted in a traditional power system during peak times. However, utilities offer DSM in order to reduce grid load during peak hours and avoid peak-to-average ratio (PAR) by encouraging end-users to shift their loads during on-peak hours. As a result of rescheduling the load, monetary advantages are gained at the end of the day, but end-user satisfaction may compromised [11, 12].
In other words, it is impossible to achieve electricity cost savings and user satisfaction simultaneously. Therefore, the constraints include everyday energy consumption, price signals, PAR, and end-user satisfaction. This has led to the development of smart EMS that can control a wide range of loads and respond to price changes [13–15]. The EMS is an essential technology for controlling future electricity distribution networks because it may move residential power usage away from peak consumption periods and minimize the amount of local generation that enters the distribution system. Due to this, they may also be able to deliver considerable cost reductions to household power consumers. Increased data interoperability, improved forecasting, and more excellent optimization of energy management systems are necessary to realize the full potential of the smart grid [16].
In the past few years, the use of RESs has been vital in minimizing global warnings. However, production is highly dependent on environmental conditions. This required an integrated and intelligent MG system to provide continuous power to the end-users [5]. Due to technological advancements, SMGs are monitored and controlled through intelligent and automated control schemes. These SMGs are small in size and offer integrated distribution networks. However, connecting the various loads, batteries, PVs, and WE to the system is vital for successfully implementing the SMGs. During this process, there exist fluctuations in power generation and usage due to the dynamic nature of the RESs. Thereby, the concept of optimal allocation of power in the home energy management system (HEMS) has a significant impact on the system. In this regard, several optimization-based and artificial intelligence-based approaches have been studied in the literature. These techniques have been designed to optimize the generation cost, pollution, and CO2 emissions subject to load balance and system constraints during scheduling time. The effective utilization and optimization of the SMGs’ components enhance system performance and provide a cost-effective distributed power generation system. The contributions of this work are highlighted below:
-
Considering the variations in power generation and consumption from RESs, it is essential to allocate power optimally in HEMS. This study aims to optimize generation cost, carbon emission, and pollution using an optimization-based approach while considering the load balance and system constraints.
-
This work implemented the NSGA, which effectively evaluates the Pareto front and offers a range of solutions that indicate trade-offs between contrasting objectives.
-
An economically distributed electrical power system is developed by the efficient use and optimization of SMG components, which also improves system reliability.
The paper is organized as follows: After a thorough introduction and forming the basis for our paper, Section 2 presents a detailed literature review of the state of the art. Section 3 discusses the proposed system model, and we show our problem statement based on the literature in Section 4. Section 5 presents experimental analysis and proposed optimization methodology. After discussing the results in Section 6, we present our conclusion and future directions in Section 7.
2 Related works
Over the past few decades, researchers worldwide have researched DR management and load scheduling in SMG. For instance, a few examples are included: in [17], a multiobjective model is used for scheduling MG status; in [18], authors worked on reducing energy consumption and waiting time of the power supply. Similarly, in [19], authors worked on improving the quality of the energy supply by using ant colony optimization approaches. The authors of [20] proposed an Adaptive Fuzzy Campus Placement Optimization Algorithm to solve both the single-objective and multiobjective optimization problems. The authors have defined an algorithm evaluated on 25 benchmark functions and then compared it with existing methods. Through results, we see that minimizing real and reactive power losses and voltage deviation, with consideration of improving voltage profiles, can be easily achieved. The non-dominated sorting genetic algorithm (NSGA) is used in [21] to address energy consumption cost and consumer satisfaction issues. The MG environment’s economic index and voltage stability problems are studied in [22] using a multiobjective optimization planning approach. In [23], load fluctuations and user satisfaction issues are addressed by using game-theoretical approaches. In addition, reference [24] used a genetic algorithm to solve demand and energy consumption issues, reference [25] worked on balancing energy demand and power supply in MG, and reference [26] proposed a multiobjective grasshopper optimization method to solve the load forecasting problem in MG.
Multiple smart homes with IoT are considered with their MGs to provide energy. MGs include distributed energy resources (DERs) such as boilers, CHP generators, as well as electrical and thermal storage systems. The DERs in a building are shared by all the homes. Authors [27] explore the integration of DERs within MGs to address energy challenges, employing a novel approach using the random forest (RF) machine learning algorithm. The experimental study considers historical data to optimize and improve DERs-based microgrid configuration, considering conflicting objectives like seasonal battery sizing and degradation, minimum generation cost, and, at the same time, reduced battery charging cost. Results are compared across various seasons with meta-heuristics and artificial intelligence methods, including particle swarm optimization and artificial neural networks.
Energy scheduling in MG can be optimized through the use of an enhanced adaptive bat algorithm (EABA) [28]. The EABA implements a system for information exchange and provides an adaptive weight to the speed of each bat in the previous generation. Furthermore, different search techniques are used to increase search performance in the early and late stages of the search. EABA’s performance is proven by scheduling the generation of distributed generators in a grid-off MG, which includes three wind power plants, two solar power plants, and a combined heat and power plant. In [29], an optimum power flow (OPF) issue is defined and addressed using the bird swarm algorithm (BSA), to reduce costs and reduce carbon emissions. The suggested solution is evaluated using an IEEE 30-bus testing system to determine the best settings while maintaining the specified limitations for active and reactive power, voltage stability, and line capacity in mind. In [30], the grey wolf optimizer (GWO), a robust swarm-based optimization algorithm inspired by the grey wolf lifestyle, is adapted to address the power scheduling problem in a smart home (PSPSH) as a multiobjective optimization problem that reduces the effect of constraints in obtaining optimal/near-optimal solutions under a set of constraints and a dynamic pricing scheme(s) produced by a power supplier company. In [31], an optimum hybrid energy system model utilizing existing PV and WE resources with battery storage to meet the electrical demands of rural communities in India. A firefly algorithm-based technique determines the best hybrid system configuration based on the lowest COE while meeting a set of reliability criteria indicated by the loss of load probability (LOLP) reliability index.
In [32], optimization of a component sizing of a grid-connected solar PV-fuel cell-based hybrid energy system to supply the electrical load demands of a small shopping complex was performed using three meta-heuristic algorithms, namely artificial bee colony, particle swarm optimization, and a hybrid of both. The trial findings from three algorithms were evaluated regarding the system’s cost-effectiveness. In [33], presents TG-MFO (Time-constrained Genetic-Moth Flame Optimization), a hybrid version of two bio-inspired heuristic algorithms, GA and moth-flame optimization (MFO), for an EMS in smart homes and buildings. Their performance in energy cost reduction, PAR minimization, and end-user discomfort minimization is examined and reviewed.
A hybrid version of two bio-inspired algorithms is proposed in [34] firefly algorithm (FA) and lion algorithm (LA) for energy scheduling to reduce the cost of energy and the waiting time of consumers or end-users in a smart home environment by categorizing all appliances into shiftable and non-shiftable appliances, and performing DSM. In [28], for optimum energy scheduling in an MG system, an EABA is suggested. EABA implements a system for information exchange and provides an adaptive weight to the speed of each bat in the previous generation.
Furthermore, different search techniques are used to increase search performance in the early and late stages of the search. EABA’s performance is proven by scheduling the generation of distributed generators in a grid-off MG, which includes three wind power plants, two solar power plants, and a combined heat and power plant. In [35], an OPF issue is defined and addressed using the bird’s swarm algorithm (BSA) to reduce costs and carbon emissions. The suggested solution is evaluated using an IEEE 30-bus testing system to determine the best settings while maintaining the limitations for active and reactive power, voltage stability, and line capacity.
In [36], the polar bear optimization (PBO) [37] strategy was used for handling the scheduling problem of demand-responsive appliances in a HEMS to reduce power consumption costs and PAR. Case studies demonstrate the approach’s usefulness for a home customer using various base loads and uninterruptible deferrable and interruptible appliances in a real-time energy price program. In [38], an energy management approach for grid-connected net zero energy buildings (NZEB) that assists in achieving a net-zero energy balance was presented, resulting in cost savings for the consumer’s net energy consumption and a lower carbon footprint. A single-objective DE optimization method is used for energy management to prune the demand for electrical energy via household appliance scheduling. In [39], the artificial ecosystem optimizer (AEO) method, inspired by energy flocking amongst living creatures in the ecosystem, is utilized for DSM as an optimization problem with restrictions on appliance start and stop times. The approach is tested on two distinct pricing schemes while considering two operating time intervals (OTI) to give the best scheduling pattern for smart homes. In [40], an artificial immune system (AIS) to solve demand response and schedule optimization. Opt-aiNet is a specific AIS that is used to solve a power system optimization problem for a domestic environment with various appliances connected to the network. At the same time, the Opt-aiNet algorithm is adapted to include complex constraints in the optimization problem and to work with many variables in this domestic environment.
In [22], the authors worked on optimal allocation and coordination by considering wind, solar, and batteries under renewable curtailment and battery degradation levels. The multiobjective optimization problem aims to maximize economic cost and voltage stability and minimize power losses during the power supply. Furthermore, the dynamic of wind and solar is handled using stochastic approaches. The proposed scheme is implemented on the IEEE 33-bus network. The simulation results demonstrated the effectiveness in maximizing the economic cost and voltage stability while the power losses were successfully reduced. In [41], authors worked on energy scheduling in the smart home environment. The two-objective optimization problem minimizes the operation cost of consumer comfort and emissions. This work is implemented on a 69-bus network and a 14-node gas network.
Furthermore, consumer demand, price, and RESs are considered uncertain entities. The simulation demonstrated the effectiveness of the scheme regardless of the operating seasons. In [18], authors worked on load scheduling in smart homes using a multiobjective optimization approach. In this work, flexible loads of AC appliances are considered. Moreover, four types of loads consisting of interruptible and deferrable loads with a combination of flexible AC loads are simulated. The simulation results demonstrated the scheme’s effectiveness for optimal scheduling of different dynamic loads. In [42], authors worked on modeling power scheduling and multi-type consumers. In this work, consumers are categorized into different groups, and energy costs and consumption levels are allocated to each group. Furthermore, the dynamic of energy and consumption is considered. The multiobjective optimization problem is used to minimize energy consumption and cost. The simulation results demonstrated that consumer satisfaction level is increased for all types of consumers.
By carefully reviewing the literature mentioned above, the following challenges and gaps have been identified and tried to address in this work. These challenges are listed below:
-
Handling multiobjective optimization: The challenge of achieving balanced conflicting objectives such as cost minimization, consumer satisfaction, and carbon reduction are challenging to solve [17].
-
Integrating renewable energy sources: Maintaining a balance between wind and solar curtailment and battery degradation while integrating renewable energy sources into microgrids [22].
-
Uncertainty management: To ensure robust scheduling and optimization, uncertainty in factors such as consumer demand, energy prices, and renewable energy sources must be addressed [41].
-
Dynamic pricing schemes: The development of strategies for optimizing energy scheduling under dynamic pricing schemes that consider varying costs and incentives during the energy scheduling process [30].
-
Modeling consumer behavior: Integrating dynamic consumer behavior models to predict and manage energy consumption optimally [42].
3 Proposed system model
This paper considers an IoT-enabled smart building with multiple smart homes and its own local MG as an energy provider. All the households, smart meters, and DERs are IoT-enabled. The MGs are comprised of DERs such as boilers and CHP generators with electrical and thermal storage systems. These DERs are shared among all homes in a building. Smart meters are electronic devices communicating between utilities and local communities through a communication link. Utility companies produce massive amounts of data, such as pricing signals, and transmit them to smart meters through a communication link. The smart meter can send this data to HEMS. The HEMS can gather data such as the appliance’s energy usage patterns, appliance’s on/off times, electricity generation data from DERs, and electricity price data from smart meters. HEMS then communicates with IoT-enabled smart appliances and performs the energy management process. Furthermore, the generated data can be stored in the data center and used on demand. All of the devices, as mentioned earlier, are IoT-enabled and connected via a communication link. The graphical representation of the proposed system model is shown in Figure 1. This work considers one CHP generator, boiler, electrical storage, and thermal storage unit. The output of CHP is 1.2 in terms of heat-to-power ratio. For electricity storage (ES), the charging and discharging efficiencies are assumed to be 95%.
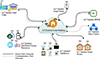 |
Fig. 1 The concept of IoT-enabled smart building EMS. |
The time is split into equal time-slots and there are 48 time intervals, each of half an hour. The appliances and their parameter are provided in Table 1. The operational constraints of this household must be fulfilled and must start their operations between between their request and end time. Based on the requirements, the system needs to determine the energy plan, start time of appliances, storage plans, and electricity bought from the grid. The objective is to find the optimum schedule for energy consumption and DER operations which minimizes electricity cost and CO2 emissions (Table 2). The details for carbon emission from CHP and boiler operations are considered to be constant (provided in Table 3). The carbon footprints of the system are estimated during the use phase, based on a functional unit of 1 kWh of electrical and thermal output for the CHP and boiler, respectively. The efficiencies for boiler and CHP are assumed to be 85% and 40%, respectively. CO2 details in Table 3 represent the total heat and electricity emissions generated by CHP based on power output. CHP has a heat-to-power ratio of 1.2 and produces 0.1821gCO2 kWh of electricity. The fuel cell for CHP is assumed to have a capacity of 10 kW with 40% electrical efficiency.
Appliances technical specifications including the rating power and time duration.
Technical parameters of DERs.
CO2 footprint for the CHP and the boiler.
Cost comparison with unscheduled scheme.
4 Problem formulation
A multiobjective optimization model of the energy consumption management problem is formulated as mixed integer linear programming that combines both economical and environmental sustainability in a multiobjective framework. The scheduling of everyday electrical appliances is based on their operating time slots, everyday electricity cost, and carbon emissions profile. The goal of this project is to lower everyday electricity costs, reduce carbon emissions, and cut off-peak power consumption. Energy costs and carbon emissions are reduced within the scope of relevant constraints, such as equipment sizing, energy demand, and thermal & electrical storage constraints.
Mathematical model of imposing constraints are:
4.1 Equipment sizing constraint
The output of each unit should remain within its designed size.
4.2 Thermal/electrical storage constraints
In a time t, the amount of energy stored is the amount of electricity stored at t − 1, plus/minus the amount of electricity charged/discharged. Here ηE is represented as a loss of electricity during the charging/discharging process. For instance, during the charging process, ηE δx
t
will be required for charging at any period δ. While in discharging, δy
t
/ηE of electricity is needed so that the customer can receive δy
t
.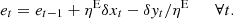 (5)
(5)
Here we assume that storing electricity is not allowed. Therefore, each storage unit must return to its original condition at the end of the day.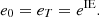 (6)
(6)
Equations (7) and (8) describe the rate of charge/discharge of electricity that is assumed to remain within the designed capacity of charging/discharging limits of the storage device.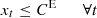 (7)
(7)
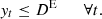 (8)
(8)
In a time t, the amount of heat stored is the amount of heat stored at t − 1, plus/minus the amount of heat charged/discharged. As in the case of electrical storage, ηTH is represented as heat loss during the charging/discharging process. At the end of each day, the stored heat must return to its original state. No heat can accumulate over the course of one day.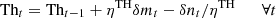 (9)
(9)
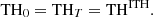 (10)
(10)
Based on the defined thermal storage capacity, the rate of charge and discharge of heat cannot exceed the design limit.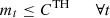 (11)
(11)
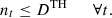 (12)
(12)
4.3 Mixed energy sources
Here, the energy demand is met by mixed energy sources such as energy generated from CHP generators, electrical storage devices, and the grid. Additionally, surplus energy is sent back to an electrical storage device. In equation (13), y
t
represents surplus energy with a minus sign. The minus sign indicates that energy is being sent to the storage device.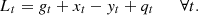 (13)
(13)
In order to satisfy heat demand, the CHP generator, boiler, heat obtained from thermal storage, and heat sent to thermal storage need to be used in combination. This is exactly similar to energy demand. As shown in equation (14), Surplus heat is represented as m
t
, and the minus sign indicates that heat is being sent to the thermal storage device.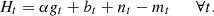 (14)
(14)
4.4 Appliance operational time constraint
All appliances must start/finish their operation within the starting/ending time. L
jit
indicates the binary variable where appliance i in a house j turns ON at time t. Each appliance must start/finish its working operation within the starting/ending time minus the appliance operational time.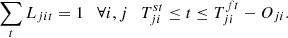 (15)
(15)
4.5 Extra charges constraint
The normal electricity price applies if, at any time, the internal grid load is below the agreed threshold value. Excess amounts are, however, accounted for and charged at a higher rate in equation (18). Moreover, the objective function has to be minimized, which implies that the β
t
value has to be minimized as well.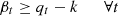 (16)
(16)
4.6 Objective function
Primarily, our objective is to reduce the overall cost of every day’s electricity. This includes the cost of purchasing electricity from the grid, the cost of electrical and thermal storage, and the cost of operating, and maintaining the CHP generator. It is mentioned that capital costs are not taken into account.![$$ {\psi }_1=\sum_t \left[\zeta (r{g}_t/{\eta }^{\mathrm{CHP}})+{a}_t{q}_t+r{b}_t/{\eta }^{\mathrm{B}}+{\mu }^{\mathrm{E}}{y}_t+{\mu }^{\mathrm{TH}}{n}_t\right]. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq17.gif) (17)
(17)
Whenever the electricity demand exceeds the agreed threshold, extra charges are taken into account in the original cost. If the demand falls below the threshold, there is no additional cost and the price reflects the real-time electricity price. Equation (18) is applied when extra electricity charges are included.![$$ {\psi }_1=\sum_t \left[\zeta (r{g}_t/{\eta }^{\mathrm{CHP}})+{a}_t{q}_t+r{b}_t/{\eta }^{\mathrm{B}}+{\mu }^{\mathrm{E}}{y}_t+{\mu }^{\mathrm{TH}}{n}_t+p{\beta }_t\right]. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq18.gif) (18)
(18)
Equation (19) includes the penalty value in the objective function for the maximum daily power demand.![$$ {\psi }_1=\sum_t \left[\zeta (r{g}_t/{\eta }^{\mathrm{CHP}})+{a}_t{q}_t+r{b}_t/{\eta }^{\mathrm{B}}+{\mu }^{\mathrm{E}}{y}_t+{\mu }^{\mathrm{TH}}{n}_t\right]+v{q}^{\mathrm{max}}. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq19.gif) (19)
(19)
Our second objective is to reduce the total CO2 emissions from three main sources such as emissions from traditional grid, CHP generators, and boiler plants.![$$ {\psi }_2=\sum_t \left[\zeta \left({\phi }^{\mathrm{CHP}}{g}_t+{\phi }^{\mathrm{G}}{q}_t+{\phi }^{\mathrm{B}}{b}_t\right)\right]. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq20.gif) (20)
(20)
We formulate the aforementioned two objectives as follows in a multiobjective problem: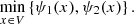 (21)
(21)
In the above equation, x represents decision variables and space V identifies feasible solutions.
5 Proposed optimization method
In this work, an enhanced fast NSGA algorithm is used to solve the multiobjective optimization problem. The proposed method was previously presented by [43] and further elaborated in our work for the understudy problem. The algorithm works through the estimation of special crowding distance, an improved binary tournament selection, an adaptive crossover scheme, and offspring generation. It is a well-known multiobjective optimization algorithm that is employed to find optimal decisions in complex decision-making problems. The workflow of the algorithm is listed below:
-
Initialization: As an initial step, the NSGA-II generates a random population of possible solutions.
-
Evaluation: The fitness of each solution is determined by evaluating it on multiple objective functions.
-
Non-dominated sorting: This step relies on the notion of non-dominance, which implies that if a solution is not dominated by anyone else, it is regarded as better. This sorting creates multiple fronts in which the first front contains solutions that are not dominated.
-
Crowding distance assignment: In the objective space, by using crowding distance, solutions are further ranked according to the density of solutions surrounding them.
-
Selection: This step involves selecting new individuals for the next generation using a combination of non-dominated sorting and crowding distance.
-
Genetic operations: By applying genetic operators, such as crossover and mutation, offspring solutions are created.
-
Termination: The algorithm iterates through genetic operation until the termination criterion is met. The algorithm reaches a maximum number of generations or successfully finds a satisfactory solution.
Next, we describe these steps along with the algorithms (see Algorithms 1, 2, and 3).
Initialization:
1: set: N
1: for i in (0, popsize) do
2: choose: Randomly choose X1 and X2
3: if Rank(X1) < Rank(X2) then
4: choose X1
5: else if Rank(X1) > Rank(X2) then
6: choose X2
7: end if
8: if Rank(X1) = Rank(X2) then
9: if SCD(X1) > SCD(X2) then
10: choose X1
11: else
12: choose X2
13: end if
14: end if
15: end for
1: Q1 = SBX + Polynomial mutation
2: Q2 = BLX − α + Polynomial mutation
3: P11 = Improved binary tournament selectiond (P1 ∪ Q1)
4: P22 = Improved binary tournament selectiond (P2 ∪ Q2)
5: Calculate PSP1 according to P11
6: Calculate PSP2 according to P22
7: if PSP1 > PSP2 then
8: Q1 = SBX + Polynomial mutation
9: else
10: Q2 = BLX – α + Polynomial mutation
11: else if
1: Input: Given Population
2: Output: The best solution
1: Init P
2: Evaluate Population P
3: while Generation < max-Generation do state Determine the fitness of P1, P2
4: Sort fast non-dominated solutions
5: Determine SCD of the individuals
6: Apply improved binary tournament-based selection(P1, P2)
7: Q1 = SBX + Polynomial mutation
8: Q2 = BLX − α + Polynomial mutation
9: P11 = Improved binary tournament selection (P1 ∪ Q1)
10: P22 = Improved binary tournament selection (P2 ∪ Q2)
11: Calculate PSP1 according to P11
12: Calculate PSP2 according to P22
13: if PSP1 > PSP2 then state choose Q1
14: else state choose Q2
15: end if
16: P1 = Improved Selection (P1 ∪ Q1)
17: P2 = Improved Selection (P2 ∪ Q2)
18: Return P1, P2
19: end while
5.1 Special crowding distance
The NSGA uses the crowd distance which calculates the density of the individuals after the sorting process. Then, it selects the individual by considering the degree of the estimated crowding distance. The crowding degree demonstrates the size of the surrounding area. For example, if the degree of the crowding distance is small, it shows that the surrounding individuals are denser. The algorithm first determines the rank of individuals in ascending order of values. The crowding degree is set to 1 for the first and last individuals. Next, determining the degree of the crowding distance for other individuals takes the form as follows:![$$ \mathrm{distance}[i]=f\left({x}_{{k}_i+1}\right)-f\left({x}_{{k}_i-1}\right)/{f}_{{k}_{\mathrm{max}}}-{f}_{{k}_{\mathrm{min}}} $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq22.gif) (22)where
(22)where 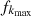 and
and 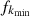 represent maximum fitness value and minimum fitness value in the kth rank respectively. Moreover,
represent maximum fitness value and minimum fitness value in the kth rank respectively. Moreover, 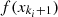 and
and 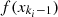 show the adjacent fitness value of the kth rank representing the ith individual.
show the adjacent fitness value of the kth rank representing the ith individual.
In general, the proposed method works as follows. First, all individuals are sorted based on the proposed sorting method. Next, the degree of the crowding distance is determined for each individual, and a special crowding distance is obtained. The individuals are given their rank based on their special crowding distance. Next, the matching of individuals is performed by taking into account those with a higher crowded degree. The special crowding distance is estimated by the following formulas:
In this case, first, we calculate the crowding decision space (CD
i,a
) and the object space (CD
i,b
) of the kth individual. Then, the special crowding distance for the kth individual is calculated as follows: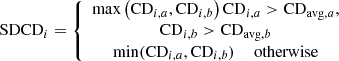 (23)where CDavg,a
and CDavg,b
show the average degree for crowding distance of the decision space and object space respectively.
(23)where CDavg,a
and CDavg,b
show the average degree for crowding distance of the decision space and object space respectively.
5.2 Improved binary tournament selection
Tournament-based selection selects a certain individual from the population, the best are used in offspring. The process repeats itself until it selects the original population size of individuals. For example, if we have N individuals in a population, there will be N number of tournaments from the population at once and obtain the best individual from the given population. In this work, the selection strategy is based on a binary tournament selection strategy which uses a degree of the crowding distance and rank of individuals as quality factors. The overall procedure is presented in Algorithm 1.
5.3 Adaptive crossover strategy
5.3.1 SBX crossover
The proposed scheme follows the SBX crossover operator used for the single-point binary for solving multiobjective optimization problems. The working of the SBX crossover operator is as follows. Let’s suppose, there are two n-dimensional parent individuals mathematically defined as: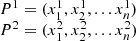 (24)
(24)
Moreover, 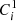 and
and 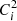 represent new individuals obtained by the crossing process. Then, to generate the next generation of individuals, the SBX function is defined as follows:
represent new individuals obtained by the crossing process. Then, to generate the next generation of individuals, the SBX function is defined as follows:![$$ {SBX}({P}^1,{P}^2)=\left\{\begin{array}{l}{C}_i^1=0.5\left[(1-\beta ){x}_i^1+(1+\beta ){x}_i^2\right]\\ {C}_i^2=0.5[(1+\beta ){x}_i^1+(1-\beta ){x}_i^2]\end{array}\right. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq31.gif) (25)where β is obtained dynamically and randomly with the help of the following equation.
(25)where β is obtained dynamically and randomly with the help of the following equation.
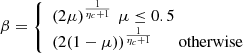 (26)where η
c
shows a custom parameter. The nature of the offspring depends on the value of η
c
e.g. the larger value generates offspring closer to the parent. Moreover, μ shows a random number in the range (0 and 1).
(26)where η
c
shows a custom parameter. The nature of the offspring depends on the value of η
c
e.g. the larger value generates offspring closer to the parent. Moreover, μ shows a random number in the range (0 and 1).
5.3.2 BLX-α crossover
The second crossover operator used in this work is BLX-α which is a blend operator. Let’s suppose the parent individuals as in 24, then the BLX crossover is obtained as:![$$ \mathrm{BLX}-\alpha ({P}^1,{P}^2)=\left\{\begin{array}{l}{C}_j^1=[(1-\beta ){x}_j^1+\beta {x}_j^2]\\ {C}_j^2=[(1-\beta ){x}_j^2+\beta {x}_j^1]\end{array}\right. $$](/articles/stet/full_html/2024/01/stet20240034/stet20240034-eq33.gif) (27)where β = (1 + 2α)U(0, 1) − α. α = 0.5 and U = (0, 1) are used.
(27)where β = (1 + 2α)U(0, 1) − α. α = 0.5 and U = (0, 1) are used.
5.3.3 Adaptive crossover
It is noted that the SBX-based crossover method showed better performance in terms of distribution and convergence of PF in single-modal multiobjective optimization problems. However, it also experienced that the SBX-based crossover method showed poor performance in terms of distribution and convergence of PF in multi-modal multiobjective optimization problems. In contrast, the BLX-α based crossover method showed good performance on solving low-dimensional multiobjective optimization problems. However, this method demonstrated poor performance in PS distribution and convergence. To address this issue, we proposed an adaptive crossover scheme for solving multiobjective optimization problems. We present a combination of crossover schemes by integrating SBX-based crossover for solving high dimensions and BLX-α for getting the Pareto solution set in solving multiobjective optimization problems. The proposed adaptive scheme creates offspring with a higher degree of crowding distance in the population. Furthermore, it also has the ability to balance the convergence of the decision space and object space. The overall scheme is depicted in Algorithm 2.
The proposed scheme integrates an adaptive crossover method for generating new offspring and an improved selection method for selecting the best individuals in the offspring in order to solve multiobjective optimization problems. The overall working of the method is shown in Algorithm 3.
6 Result and discussions
This section discusses the simulation and results of our applied scheme. DERs operation and appliances are scheduled for 24 h, from 8 am to 8 am on the next day. The model is implemented in Matlab 2021a on a laptop with Intel Core i5-4300 CPU, 2.50 GHz processor, and 4GB of RAM.
Three pricing schemes are applied for the simulation of cost and carbon emission minimization schemes. Figure 2 shows the Pareto optimal solutions to demonstrate the trade-off between cost and carbon emissions. The points on these curves are marked with letters As, Bs, and Cs. Points As and Cs are the points where only a single objective is considered, for instance, point As only minimizes cost, and point Cs considers only CO2 emissions. Both these become a single objective, whereas, Bs are the points of our interest showing a trade-off between cost and CO2 emissions. These five curves represent different pricing schemes such as RTP, CPP-DC, and CPP-PDC as discussed in Section 6.1.
 |
Fig. 2 Pareto fronts for cost and carbon emission. |
6.1 Electricity demand schedule
Figure 2 shows that all Cs (C1–C5) are very similar, which means that electricity balances for this point are the same. For this reason, only one figure (Fig. 3) is given for all generic Cs. This is a single objective optimization, their demand is scheduled only for minimizing the carbon emissions. However, it is also noteworthy that cost is different when the single objective cost is minimized. For point Cs (CO2 minimization), it is observed that our algorithm has scheduled CHP operation at its maximum capacity during most of the time periods due to low CO2 intensity, whereas the remaining demand is covered by buying electricity from the conventional power grid. It is also noticed that there are two peaks, one in the early morning at 08:00 and the other in the evening at 16:30 due to operations of inflexible appliances. When CO2 intensity is low, electricity demand is fulfilled by scheduling the energy bought from the grid as provided in Figure 4. The ES is charged at 22:00 and 22:30 and discharged at 8:00 and 8:30.
 |
Fig. 3 Energy balance for point Cs. |
 |
Fig. 4 Representation of carbon emission over 24 h period. |
Figure 5 shows energy balances for cost and trade-off schemes under real-time pricing schemes. For point A1 (cost minimization), the only objective is to minimize the total cost based on a real-time pricing scheme, so electricity demand is scheduled solely on the pricing signal without considering CO2 footprints. Figure 5a shows that most of the demand is scheduled in the early morning hours between 4:00 and 7:00 when energy prices are low (see Fig. 6). In the case of point B1 (trade-off between cost and CO2), the peak energy demand hours are between 3:00 and 6:00 in the morning. ES charging and discharging are also scheduled accordingly as provided in Figure 5b, and ES works more frequently at both these points as compared to point Cs. CHP is also operating at its full capacity during most of the hours not only in the daytime but also at night.
 |
Fig. 5 Energy balances under RTP for A1 and B1. |
 |
Fig. 6 Real-time pricing signal between 12:00 midnight and the following midnight. |
Figure 7 shows electricity demand for A2–A4 and B2–B4 under CPP-PDC with three thresholds considered in this work. The total energy demand is distributed over 24 h for points A2–A4, which resulted in a more flattened curve than point A1 (except the time when inflexible households are operating). Threshold values in peak demand avoid the creation of peak by operating CHP at full capacity during most of the hours, thus avoiding peak demand penalty. For B2–B4, the energy demand is scheduled between 20:00 and 0:00 as compared to B1. This shows conflicting objectives between electricity prices and carbon footprints. The demand curves are more or less similar, except from 9:00 to 16:30. Furthermore, the peak power demand from the grid has also been curtailed. Figure 8 shows the results of scheduling under CPP-PDC for points A5 and B5. It can be observed from the figures that maximum energy demand from power grids is relatively low as compared to Figures 5 and 7. For A5, electricity is only bought from the grid during periods when there are low prices. For B5, the demand is scheduled at the periods according to the trade-off between the carbon emissions profile and electricity prices. ES is charged at times of low prices and discharged at times of high prices of electricity from the grid. It is also observed that ES is less frequently used due to low heat demand in summer. There is a limited electricity output from CHP, ES usage is also low. The ES is only used if there is a significant difference in prices, and not used if maintenance cost and the cost of charging discharging energy loss surpasses the price difference.
 |
Fig. 7 Energy balances under CPP-PDC (Threshold = 60 kW, 40 kW, and 20 kW). |
 |
Fig. 8 Energy balances under CPP-DC. |
In terms of total and maximum electricity demand, CPP-PDC minimizes the total demand over the agreed threshold, whereas CPP-PDC minimizes maximum power demand from the grid. Peak power demand and total power demand from the grid exceeding the agreed demand threshold are provided in Table 4. CPP-PDC price minimizes the maximum power demand from the grid and total demand over the agreed threshold for most of the points. It has reduced the maximum as well as total power demand from the grid, and hence carbon emissions. The total electricity demand from the grid increases when carbon emission constraints become tight (B3–B4). When the CHP is operating at its maximum capacity, the remaining power requirements are covered by the grid. 60 kW threshold is good for all cases; however, the penalty is charged even if the threshold is set at 60 kW and even if CHP is operating at full capacity. This is due to some inflexible tasks which must operate at their fixed time. For points A5 and B5, the maximum power demand from the grid is minimized. The maximum power demand is reduced up to 22% as compared to A2. The maximum carbon emissions are similar to the results of CPP-PDC with thresholds. Table 4 provides the total demands under the RTP and CPP-DC price scheme. The total power demand above the agreed thresholds of the other two pricing schemes is higher than the individual power demands of the CPP-PDC pricing schemes (see Tab. 4).
6.2 Heat demand schedule
Heat balances for points A1–B1 and A2–B2 are provided in Figure 9 under RTP and PDC with 60 kW threshold, respectively. Under the RTP scheme, the CHP generator operates less frequently when only cost is considered. The reason for this is low heat demand in summer and CHP can’t produce more electricity unless the heat produced as a result is consumed or stored in thermal storage. Thermal storage balances the CHP output but is limited by its capacity. During the time interval when electricity demand is high but heat demand is low, the generated heat is stored in thermal storage and released at the time of heat demand. So, thermal storage stores heat in the daytime and discharges at night. The thermal storage charges eight times both, in the case of cost-minimizing and trade-off schemes but at different time intervals. However, CHP operates at full capacity when CO2 emissions are taken into consideration. Since the heat requirements are provided rather than the power demand, So the heat balances for points As and Bs are similar in the case of CPP-PDC and CPP-DC pricing schemes. So, only the balances for heat are provided for A2 and B2.
 |
Fig. 9 Heat balances. |
7 Conclusion
This paper proposes a non-dominated sorting genetic algorithm approach for optimally scheduling the energy consumption profile of multiple smart homes in an MG environment. We consider two objective optimization problems, such as the minimization of economic costs and environmental impacts. In this work, an IoT-enabled smart building is considered with 30 smart homes with its own local MG as an energy provider. All the households, smart meters, and DERs are IoT-enabled. The MGs are comprised of DERs, such as a boiler and a CHP generator with thermal and electrical storage. These DERs are shared among all homes in a building. Results show that the proposed scheme efficiently schedules electrical appliances and optimizes the operation of DERs in such a way that minimizes both consumers’ electrical bills by avoiding peak hour schedules and CO2 emissions by utilizing local DERs as a source of energy.
With the proliferation of objectives and decision variables, the complexity of multiobjective optimization problems grows exponentially, making them computationally challenging. The curse of dimensionality is one of the limitations of solving multiobjective optimization problems. Additionally, due to the curse of dimensionality, it becomes increasingly difficult to identify the entire Pareto front, which represents the trade-offs between objectives. Further, finding solutions that satisfy all objectives simultaneously is difficult since it requires making trade-offs between conflicting objectives. In the future, we aim to extend the approach by incorporating the communication bandwidth of IoT-enabled devices, which also influences the optimization outcomes. In addition, we will focus on the scalability and applicability of the proposed method in the real-world application.
Funding
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Authors contribution statement
Awais Manzoor: Conceptualization, Methodology, Software, Writing – Original Draft, Formal Analysis, Writing – Reviews and Editing. Waseem Akram: Methodology, Writing – Original Draft, Investigation. Malik Ali Judge: Software, Formal Analysis, Writing – Original Draft. Hasan Ali Khattak: Conceptualization, Formal Analysis, Writing – Reviews and Editing.
References
- Blanco H., Faaij A. (2018) A review at the role of storage in energy systems with a focus on power to gas and long-term storage. Renew. Sustain. Energy Rev. 81, 1049–1086. [CrossRef] [Google Scholar]
- Ziadeh A., Abualigah L., Elaziz M.A., Şahin C.B., Almazroi A.A., Omari M. (2021) Augmented grasshopper optimization algorithm by differential evolution: A power scheduling application in smart homes, Multimed. Tools Appl. 80, 21, 31569–31597. [CrossRef] [Google Scholar]
- Abbassi A., Mehrez R.B., Touaiti B., Abualigah L., Touti E. (2022) Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm, Optik 253, 168600. [CrossRef] [Google Scholar]
- Eltigani D., Masri S. (2015) Challenges of integrating renewable energy sources to smart grids: A review, Renew. Sustain. Energy Rev. 52, 770–780. [CrossRef] [Google Scholar]
- Ma R., Chen H.-H., Huang Y.-R., Meng W. (2013) Smart grid communication: Its challenges and opportunities, IEEE Trans. Smart Grid 4, 1, 36–46. [CrossRef] [Google Scholar]
- Ayodele E., Misra S., Damasevicius R., Maskeliunas R. (2019) Hybrid microgrid for microfinance institutions in rural areas – a field demonstration in West Africa, Sustain. Energy Technol. Assess. 35, 89–97. [Google Scholar]
- Vardakas J.S., Zorba N., Verikoukis C.V. (2015) A survey on demand response programs in smart grids: Pricing methods and optimization algorithms, IEEE Commun. Surv. Tutor. 17, 1, 152–178. [CrossRef] [Google Scholar]
- Judge M.A., Khan A., Manzoor A., Khattak H.A. (2022) Overview of smart grid implementation: Frameworks, impact, performance and challenges, J. Energy Storage 49, 104056. [CrossRef] [Google Scholar]
- Gelazanskas L., Gamage K.A.A. (2014) Demand side management in smart grid: A review and proposals for future direction, Sustain. Cities Soc. 11, 22–30. [CrossRef] [Google Scholar]
- Esther B.P., Kumar K.S. (2016) A survey on residential demand side management architecture, approaches, optimization models and methods, Renew. Sustain. Energy Rev. 59, 342–351. [CrossRef] [Google Scholar]
- Judge M.A., Manzoor A., Maple C., Rodrigues J.J., ul Islam S. (2021) Price-based demand response for household load management with interval uncertainty, Energy Rep. 7, 8493–8504. [CrossRef] [Google Scholar]
- Manzoor A., Javaid N., Ullah I., Abdul W., Almogren A., Alamri A. (2017) An intelligent hybrid heuristic scheme for smart metering based demand side management in smart homes, Energies 10, 9, 1258. [CrossRef] [Google Scholar]
- Zhou B., Li W., Chan K.W., Cao Y., Kuang Y., Liu X., Wang X. (2016) Smart home energy management systems: Concept, configurations, and scheduling strategies, Renew. Sustain. Energy Rev. 61, 30–40. [CrossRef] [Google Scholar]
- Bayram I.S., Ustun T.S. (2017) A survey on behind the meter energy management systems in smart grid, Renew. Sustain. Energy Rev. 72, 1208–1232. [CrossRef] [Google Scholar]
- Rathor S.K., Saxena D. (2020) Energy management system for smart grid: An overview and key issues, Int. J. Energy Res. 44, 6, 4067–4109. [CrossRef] [Google Scholar]
- Mourshed M., Robert S., Ranalli A., Messervey T., Reforgiato D., Contreau R., Becue A., Quinn K., Rezgui Y., Lennard Z. (2015) Smart grid futures: Perspectives on the integration of energy and ICT services, Energy Proc. 75, 1132–1137. [CrossRef] [Google Scholar]
- Khalili T., Nojavan S., Zare K. (2019) Optimal performance of microgrid in the presence of demand response exchange: A stochastic multiobjective model, Comput. Electr. Eng. 74, 429–450. [CrossRef] [Google Scholar]
- Muralitharan K., Sakthivel R., Shi Y. (2016) Multiobjective optimization technique for demand side management with load balancing approach in smart grid, Neurocomputing 177, 110–119. [CrossRef] [Google Scholar]
- Silva B.N., Han K. (2019) Mutation operator integrated ant colony optimization based domestic appliance scheduling for lucrative demand side management, Future Gener. Comput. Syst. 100, 557–568. [CrossRef] [Google Scholar]
- Sunil A., Venkaiah C. (2024) Multi-objective adaptive fuzzy campus placement based optimization algorithm for optimal integration of DERs and DSTATCOMs, J. Energy Storage 75, 109682. [CrossRef] [Google Scholar]
- Cortes-Arcos T., Bernal-Agustín J.L., Dufo-Lopez R., Lujano-Rojas J.M., Contreras J. (2017) Multi-objective demand response to real-time prices (RTP) using a task scheduling methodology, Energy 138, 19–31. [CrossRef] [Google Scholar]
- Taha H.A., Alham M., Youssef H.K. (2022) Multi-objective optimization for optimal allocation and coordination of wind and solar DGS, BESSs and capacitors in presence of demand response, IEEE Access 10, 16225–16241. [CrossRef] [Google Scholar]
- Lu Q., Zhang Y. (2022) Demand response strategy of game between power supply and power consumption under multi-type user mode, Int. J. Electr. Power Energy Syst. 134, 107348. [CrossRef] [Google Scholar]
- Liu Y., Ćetenović D., Li H., Gryazina E., Terzija V. (2022) An optimized multi-objective reactive power dispatch strategy based on improved genetic algorithm for wind power integrated systems, Int. J. Electr. Power Energy Syst. 136, 107764. [CrossRef] [Google Scholar]
- Noor S., Yang W., Guo M., van Dam K.H., Wang X. (2018) Energy demand side management within micro-grid networks enhanced by blockchain, Appl. Energy 228, 1385–1398. [CrossRef] [Google Scholar]
- Wang J., Zhang L., Liu Z., Niu X. (2022) A novel decomposition-ensemble forecasting system for dynamic dispatching of smart grid with submodel selection and intelligent optimization, Expert Syst. Appl. 201, 117201. [CrossRef] [Google Scholar]
- Vaish J., Tiwari A.K., Kaimal S. (2024) Multi-objective optimization of distributed energy resources based microgrid using random forest model, Bull. Electr. Eng. Inform. 13, 1, 67–75. [CrossRef] [Google Scholar]
- Yang Q., Dong N., Zhang J. (2021) An enhanced adaptive bat algorithm for microgrid energy scheduling, Energy 232, 121014. [CrossRef] [Google Scholar]
- Ahmad M., Javaid N., Niaz I.A., Almogren A., Radwan A. (2021) A bioinspired heuristic algorithm for solving optimal power flow problem in hybrid power system, IEEE Access 9, 159809–159826. [CrossRef] [Google Scholar]
- Makhadmeh S.N., Al-Betar M.A., Alyasseri Z.A., Abasi A.K., Khader A.T., Damaševičius R., Mohammed M.A., Abdulkareem K.H. (2021) Smart home battery for the multi-objective power scheduling problem in a smart home using grey wolf optimizer, Electronics 10, 4, 447. [CrossRef] [Google Scholar]
- Sanajaoba S. (2019) Optimal sizing of off-grid hybrid energy system based on minimum cost of energy and reliability criteria using firefly algorithm, Sol. Energy 188, 655–666. [CrossRef] [Google Scholar]
- Singh S., Chauhan P., Singh N. (2020) Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm, Int. J. Hydrogen Energy 45, 16, 10070–10088. [CrossRef] [Google Scholar]
- Ullah I., Hussain S. (2019) Time-constrained nature-inspired optimization algorithms for an efficient energy management system in smart homes and buildings, Appl. Sci. 9, 4, 792. [CrossRef] [MathSciNet] [Google Scholar]
- Ullah H., Khan M., Hussain I., Ullah I., Uthansakul P., Khan N. (2021) An optimal energy management system for university campus using the hybrid firefly lion algorithm (fla), Energies 14, 19, 6028. [CrossRef] [Google Scholar]
- Ma X., Mu Y., Zhang Y., Zang C., Li S., Jiang X., Cui M. (2022) Multiobjective microgrid optimal dispatching based on improved bird swarm algorithm, Glob. Energy Interconnect. 5, 2, 154–167. [CrossRef] [MathSciNet] [Google Scholar]
- Iqbal M.M., Zia M.F., Beddiar K., Benbouzid M. (2020) Optimal scheduling of grid transactive home demand responsive appliances using polar bear optimization algorithm, IEEE Access 9, 222285–222296. [CrossRef] [Google Scholar]
- Połap D., Woźniak M. (2017) Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism, Symmetry 9, 10, 203. [CrossRef] [Google Scholar]
- Madathil D., Pandi V.R., Nair M.G., Jamasb T., Thakur T. (2021) Net zero energy in a residential building using heuristic optimization solution, J. Control Autom. Electr. Syst. 32, 2, 458–471. [CrossRef] [Google Scholar]
- Mouassa S., Tostado-Véliz M., Jurado F. (2021) Efficient power scheduling in smart homes using a novel artificial ecosystem optimization technique considering two pricing schemes, Int. J. Emerg. Electr. Power Syst. 22, 643–660. [MathSciNet] [Google Scholar]
- Navarro-Caceres M., Herath P., Villarrubia G., Prieto-Castrillo F., Kumar Venyagamoorthy G. (2018) An evaluation of a metaheuristic artificial immune system for household energy optimization, Complexity 2018. [CrossRef] [Google Scholar]
- Safaie A.A., Bidgoli M.A., Javadi S. (2022) A multi-objective optimization framework for integrated electricity and natural gas networks considering smart homes in downward under uncertainties, Energy 239, 122214. [CrossRef] [Google Scholar]
- Lu Q., Zhang Y. (2022) A multi-objective optimization model considering users’ satisfaction and multi-type demand response in dynamic electricity price, Energy 240, 122504. [CrossRef] [Google Scholar]
- Deng W., Zhang X., Zhou Y., Liu Y., Zhou X., Chen H., Zhao H. (2022) An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems, Inf. Sci. 585, 441–453. [CrossRef] [Google Scholar]
All Tables
Appliances technical specifications including the rating power and time duration.
All Figures
 |
Fig. 1 The concept of IoT-enabled smart building EMS. |
| In the text | |
 |
Fig. 2 Pareto fronts for cost and carbon emission. |
| In the text | |
 |
Fig. 3 Energy balance for point Cs. |
| In the text | |
 |
Fig. 4 Representation of carbon emission over 24 h period. |
| In the text | |
 |
Fig. 5 Energy balances under RTP for A1 and B1. |
| In the text | |
 |
Fig. 6 Real-time pricing signal between 12:00 midnight and the following midnight. |
| In the text | |
 |
Fig. 7 Energy balances under CPP-PDC (Threshold = 60 kW, 40 kW, and 20 kW). |
| In the text | |
 |
Fig. 8 Energy balances under CPP-DC. |
| In the text | |
 |
Fig. 9 Heat balances. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.