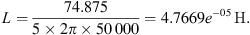| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Decarbonizing Energy Systems: Smart Grid and Renewable Technologies
|
|
|---|---|---|
| Article Number | 86 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.2516/stet/2024064 | |
| Published online | 23 October 2024 | |
Regular Article
Design and implementation of magnetically coupled inductive power transfer system for electric vehicle charging applications
Department of Electrical and Electronics Engineering, Vignan’s Foundation for Science, Technology and Research, Guntur 522213, Andhra Pradesh, India
* Corresponding authors: dean_res@vignan.ac.in (G. Srinivas Rao); arvb_eee@vignan.ac.in (A.R. Vijay Babu)
Received:
11
May
2024
Accepted:
7
August
2024
A research paper or proposal on designing a 1.6 kW Resonant Inductive Power Transfer (IPT) system for electric vehicles (EVs). Design, Modeling, and Analysis of a 1.6 kW Resonant IPT System for EVs. To Enhance Design Performance: Improve the efficiency and effectiveness of power transfer compared to traditional EV charging systems. Conduct Loss Analysis and Analyze and minimize losses associated with the IPT system. The Advantage Highlight advantages of the proposed system over existing EV charging methods. Methodology, Integration with AC Grid: Despite EV systems being connected to the grid, this research proposes further integration and improvement using resonant (Compensated Network) circuits within IPT systems. Resonant Circuit Utilization: By matching the supply frequency with the circuit’s resonant frequency, optimal performance is achieved, addressing current IPT system drawbacks. Implementation Steps, Simulation: Evaluate primary and secondary circuits through simulation. Component Selection: Determine component values based on derived equations. Hardware Implementation: Construct the system in hardware based on simulation results. Feasibility Testing: Validate calculations through simulation and practical hardware testing. Contribution, this research aims to contribute to the field by demonstrating, improved performance through resonant IPT systems. Feasibility of integrating such systems into EV applications. Practical benefits over conventional EV charging methods. By leveraging resonant circuits in IPT systems, this study aims to demonstrate enhanced performance and efficiency suitable for EVs, thereby contributing to the advancement of EV technology and grid integration. This structured summary encapsulates the key aspects and goals of the research paper as described.
Key words: Power electronic topologies / Performance evaluation / Coupling coils / Simulation analysis / Inductive power transfer
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Electric vehicles (EVs), focusing particularly on advancements in technology and infrastructure, Energy Sources: You emphasize the use of renewable energy sources like solar, wind, and geothermal for powering electric automobiles [1, 2]. This reduces reliance on fossil fuels and promotes green energy. Battery Technology, Greater battery power density is highlighted as crucial for improving the range of electric cars. Advancements in battery technology, materials science, and chemistry are essential for boosting energy storage capacity and enhancing efficiency [3, 4]. Hybrid and Fuel Cell Technologies, the potential of fuel cell and plug-in hybrid technologies to extend the range and efficiency of EVs, suggests a complementary approach alongside battery-EVs. Stationary Wireless Charging: Introducing stationary wireless charging stations is proposed as a solution to charging range limitations [5–7]. This technology allows EVs to recharge while parked, thus minimizing range anxiety and making electric cars more convenient. Infrastructure and Collaboration: Collaboration between the automotive industry, energy sector, and governments is stressed as necessary to invest in research and development of EV technologies and infrastructure [8, 9]. Standardization of wireless charging systems is also highlighted to facilitate easier adoption and interoperability [10, 11].
Economic Viability, Ensuring that charging infrastructure is economically feasible through financial incentives, public-private partnerships, and cost-effective deployment strategies is seen as crucial for the widespread adoption of EVs [12, 13]. Overall, your argument underscores the importance of technological innovation, infrastructure development, and collaborative efforts to overcome barriers and make EVs a practical and successful option for personal mobility [14, 15].
Wireless power transfer (WPT) systems need high-frequency and high-power power electronic converters for long-distance power transfer [16]. High-frequency and high-power power electronic converter research is challenging and interesting. Effective wireless power transmission requires these converters [17, 18].
Current Converter Problems: Switching losses, high Electro Magnetic Interference (EMI), and excessive EMI are examined in current hard-switched and pulse-width modulation (PWM) converters [19, 20]. To overcome these constraints, resonant power converters were developed. The presented control method regulates load power independent of supply voltage and coupling transients. Testing this control method by altering the air gap between coils focuses on accurate output power regulation [21, 22]. Inductive Power Transfer (IPT) System: IPT systems operate between 10 and 100 kHz, experiencing switching losses in converters and copper and core losses in the coupler [23, 24]. Explaining ferrite and Litz wire choices to reduce eddy currents and losses. Core loss in circular pad constructions is analyzed using finite-element analysis (FEA). Litz wire reduces transformer winding loss by minimizing high-frequency eddy current losses [24, 25]. The study emphasizes the need to select the right Litz-wire type during design to ensure that AC loss is reduced more than DC loss, especially in medium-frequency applications [26, 27]. Simulation and test bench data are presented in the book to examine transmitting 1.6 kW of electric power [28]. The setup includes transmitter coils in parking spots, a parking lot to shield the subsurface transmitter coil, and a receiver coil on a small two-seater EV [29, 30]. In the third portion, transmitter and receiver coils, compensating circuits, power electronic topologies, and transmitter/receiver control are briefly discussed and evaluated for flat-rate pricing [31, 32]. To reduce costs and affect coupling coefficients, the transmitter coil length might be increased [33, 34].
Inside this pertains to the development and evaluation of a flat-rate pricing strategy. Section 2 addresses the design of transmitter and receiver coils. The transmitter coil is lengthened relative to the receiving coil to reduce the expenses associated with the transmitter circuit. The low coupling coefficients between the transmitter and receiving coils are due to this imbalance. Comparisons are conducted between the estimated self and mutual inductance of the transmitter and receiving coils and the real measurements. Section 3 covers compensatory circuit design, power electronic topologies, and transmitter/receiver control. Compensation circuits, when built and adjusted precisely, enhance power transfer in situations with low coupling coefficients.
2 Magnetic coupling coils and compensation network characterises
To save expenses related to static charging infrastructure, a stationary transmitter coil was used instead of a receiving coil. The coupling coefficient decreases between the transmitter and receiver coils due to the mismatch, leading to a decrease in transmitted power. For efficient power transmission, it is crucial to carefully design the transmitter and reception coils, taking into account both self and mutual inductance. This section describes the design of the transmitter coil and compares it with the measurements. The next section will include the receiver coil design, measured findings, and a visual representation of the design arrangement. Two primary coils are employed for the gearbox, while secondary coils are utilised for receiving [35, 36].
2.1 Primary coil (transmitter coil)
A rectangular coil with dimensions of 475 cm by 7.8 m and consisting of 16 turns has been built for the transmitter. Figure 1 displays a schematic of the transmitter coil utilised in this research [17].
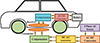 |
Fig. 1 Basic structure of IPT charging system of EVs. |
Handmade coils led to variations in geometric qualities throughout production. The actual characteristics of the produced coils differ from the expected values in several aspects. Figure 2 displays the completed coil, and Tables 1 and 2 provide the obtained geometric and self-inductance values [18].
 |
Fig. 2 Transmitter coils used in this research. (a) Spiral circular type coil. (b) Spiral Square type coil. |
Ideal geometric parameter.
Practical dimensions for manufacturing coils.
The Inductance Capacitance and Resistance (LCR) metre was utilised to manually modify the air gap until achieving a mutual inductance of 41 μH with a 16.5 cm air gap, after the creation of the analytical formula for mutual inductance. Compatibility is validated when all measured capacitances fall within the specified range [19]. The simulation findings, when integrated with the parameters specified in SAE J2954, correspond with the theoretical analysis, validating the suggested method’s suitability and effectiveness for interoperability testing. One may get the inductance of a rectangular coil by applying the equation (1).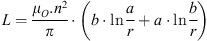 (1)a, b, r, and n represent the size of wires and the number of turns in a coil. The transmitter coil in Figure 1 has dimensions of 7.8 m for a, 6.3 m for b, and 16 turns for n. The coils used in this investigation were constructed from 3 mm Litz wire capable of carrying a current of 40-A. The research calculated the inductance of the transmitter coil to be 398 μH for circular coils and 107 μH for square coils using equation (1). The inductance and Q-factor of the transmitter coil were measured in a shielded environment using an LCR metre by varying the frequency. Figure 3 displays the transmitter coil that was measured [37, 38].
(1)a, b, r, and n represent the size of wires and the number of turns in a coil. The transmitter coil in Figure 1 has dimensions of 7.8 m for a, 6.3 m for b, and 16 turns for n. The coils used in this investigation were constructed from 3 mm Litz wire capable of carrying a current of 40-A. The research calculated the inductance of the transmitter coil to be 398 μH for circular coils and 107 μH for square coils using equation (1). The inductance and Q-factor of the transmitter coil were measured in a shielded environment using an LCR metre by varying the frequency. Figure 3 displays the transmitter coil that was measured [37, 38].
 |
Fig. 3 Photograph of the measured transmitter coil. |
Figure 4 shows the frequency-dependent inductance and Q-factor of the transmitter coil. Figure 5 shows the inductance represented by a solid blue line and the Q-factor by a dashed red line [23].
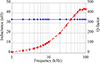 |
Fig. 4 Quantified frequency-related transmitter coil inductance and Q-factor. The solid blue line indicates inductance, whereas the dashed red line shows Q-factor [24]. |
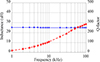 |
Fig. 5 Displays the inductance and Q-factor of the receiver coil at different frequencies. The solid blue line represents inductance, whereas the dashed red line represents Q-factor. |
Figure 4 displays the measured inductance of the transmitter coil as 398 μH, in accordance with equation (1). The Q-factor of the transmitter coil peaked at 440 at a frequency of 90 kHz [25].
2.2 Secondary coil (receiver coil)
A circular coil with a diameter of 475 cm and 15 turns was made for the receiver. Figure 2 shows the transmitter and receiver coil used in this study. The ferrite and aluminium insulate the test vehicle’s body from the magnetic field of the transmitter coil while the reception coil is operational in an electric automobile. Equation (2) calculates the inductance of a circular coil [26].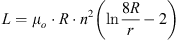 (2)
(2)
R represents the average radius of the coil. r and n are important, much like equation (1). Equation (2) calculated the inductance of the receiving coil as 107 μH using an average coil radius (R) of 0.06 m and a wire radius (r) for the transmitter coil. The inductance and Q-factor of the receiving coil changed depending on the frequency, similar to the transmitter coil. Figure 2b displays the receiver coil that was measured. Figure 5 displays the inductance and Q-factor of the frequency-based receiver coil. Figure 5 displays inductance represented by a solid blue line and Q-factor by a dashed red line [27].
The receiving coil’s inductance was 107 μH, according to equation (2) with an estimated average radius of 0.06 m. The graph shows that the receiver coil has a maximum Q-factor of 280 at a frequency of 100 kHz [39].
2.3 Coupling coefficient of the transmitter and receiver coils
In Figure 6, the coupling coefficient k is directly proportional to the ratio of the overlapping coil area to the transmitter coil’s area and inversely proportional to the cube of the distance between the coils when the receiver coil is positioned above the transmitter coil at height h. When b < 2R, equation (3) may be utilised to determine k [29].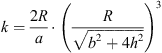 (3)
(3)
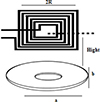 |
Fig. 6 Interoperable coupling coils. |
Figure 7 shows the measured coupling coefficient plotted against h, compared to the value obtained from equation (3).
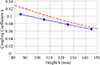 |
Fig. 7 The coupling coefficient k changes with the height h. The solid blue line represents the observed value, whereas the dashed red line represents the value calculated using equation (3). |
The measured values in Figure 8 correspond with the estimate. Establishing the height h as 100 mm led to the calculation of the coupling coefficient k as 0.09. Employing a bigger transmitter coil can decrease the cost per unit mile of the infrastructure by necessitating less power electronic equipment and fewer compensating circuits for the same road length. Equation (4) shows that the coupling coefficient k decreases as the length (a) of the transmitter coil increases. A smaller value of k leads to less power transfer efficiency (ϋ) and available power for the system. Analyse the circuit in Figure 9 to determine the maximum power transfer efficiency (ϋ) of the system [30].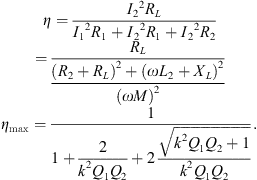 (4)
(4)
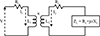 |
Fig. 8 A schematic circuit design was utilised to analyse the potential maximum power transfer efficiency. |
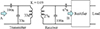 |
Fig. 9 This investigation’s transmitter and receiver circuit diagram. |
To achieve the highest power transfer efficiency as defined in equation (5), the appropriate load must be applied as determined by the subsequent equation [31].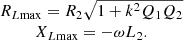 (5)
(5)
With a separation of 100 mm between the receiver coil and the transmitter coil, operating at a frequency of 90 kHz, and having values of k = 0.09, Q1 = 440, and Q2 = 280. Equation (5) was used to determine that the system’s maximum power transfer efficiency is 94%. Maximum power transfer efficiency is unattainable because of the challenge in choosing a suitable load. Compensation circuits for the transmitter and receiver must be carefully designed to avoid additional reductions in power transfer efficiency. The following section will discuss the design of the compensating circuits [32].
2.4 Compensation circuits
In low coupling coefficient circumstances, the compensating circuit uses two resonators to improve performance. Extra resonators assist tune the system for optimal resonance when the coupling is low. A key feature of the compensation circuit is its ability to precisely adjust resonance frequency. Flexibility is needed to maintain resonance with low transmitter-receiver coupling coefficients. Both transmitter and receiver have compensating circuits [33].
Dual-sided compensation improves performance at both ends of the IPT system [34]. To assess circuit performance, the simulation may test its behaviour under various conditions. Simulation can evaluate resonance frequency, efficiency, and power transmission [35]. Comparing simulated and measured properties validates simulation model accuracy [36]. Disparities can be studied to improve simulation precision or identify performance-affecting real-world factors [37]. Essential to the study, providing information on the compensating circuit’s efficiency with two resonators. Simulation and observed data will be used to understand the circuit’s behaviour and its influence on the IPT system with low coupling coefficients.
The simulation frequency of 78 kHz suggests that the system operates in the high-frequency range. The shapes of the voltage and current waveforms provide insights into the rectifier’s performance, including its efficiency, power factor, and potential issues like harmonics Analyze the relationship between voltage and current waveforms at both points A and B to understand power transfer efficiency. Look for any distortions or abnormalities in the waveforms that might indicate issues such as harmonics or undesired behaviours. Consider how well the rectifier is performing its intended function, and if needed, optimize its design for better overall system performance.
A technical analysis or experiment related to inductive charging systems for EVs. Let’s break down the key points based on your description, Phase Mismatch and Power Factor, Figures 10, 11 and 12 illustrate a 20° phase mismatch between voltage and current at locations A and B.
 |
Fig. 10 Exhibits A’s simulated voltage and current. The dashed red line denotes voltage, whereas the solid blue line shows current. |
 |
Fig. 11 Simulation of B’s voltage and current. The dashed red line denotes voltage, whereas the solid blue line shows current. |
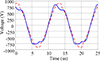 |
Fig. 12 Displays the simulated and actual voltage of the transmitter coil. The solid blue line shows the actual measurement, while the dashed red line indicates the simulated result. |
The power factor (cos ϕ) is reported to be 0.94. A high power factor indicates efficient delivery of electricity, minimizing reactive power losses. Measurement Environment, Power, current, and voltage measurements were conducted in a secure environment, ensuring accurate and reliable data collection. Simulation vs. Measurement, Figures 13–15 compare simulation results with actual measurements. In Figures 13 and 14, the transmitter coil voltage and current are depicted. The solid blue line represents the measured data, while the dashed red line represents simulated data.
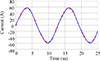 |
Fig. 13 Compares transmitter coil current simulation and measurement. The solid blue line indicates the measured value, while the dashed red line shows the simulation. |
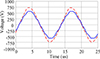 |
Fig. 14 Displays simulated and observed receiver coil voltage. The solid blue line indicates the measured value, while the dashed red line shows the simulation. |
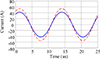 |
Fig. 15 Displays measured and simulated receiving coil current. The solid blue line shows actual data, whereas the dashed red line models it. |
The comparison between simulation and measurement findings helps validate the accuracy of the simulation model against real-world performance. An experimental setup or analysis focused on evaluating the performance of an inductive charging system. The emphasis on phase mismatch, power factor, and the comparison between simulated and measured data underscores the importance of ensuring efficiency and reliability in WPT technologies for EVs. This type of analysis is crucial for optimizing system design and enhancing the practicality of inductive charging solutions in real-world applications.
The transmitter coil voltage and current match the model’s Figures 13 and 14. Figure 14 shows that the transmitter coil’s current is less than 40 A, the study’s Litz wire’s maximum capacity. The receiving coil voltage and current are shown in Figures 14 and 15.
Figures 14 and 15 show voltage and current readings that match the model. The system provided 1.176 kW to the load, according to a power meter. Power transmission efficiency was 92.8%. The waveform distortion in Figures 14 and 15 causes the disparity between equation (5)’s measured and anticipated values.
3 Resonant circuit of WPT system
Inductive charging systems for EVs. Here’s a breakdown and clarification of your points, Power Conversion Efficiency: Inductive charging systems for EVs rely on power electronics to achieve maximum efficiency in converting power. This efficiency is crucial for early adoption and widespread use of wireless charging technology in EVs. Figures 16 and 17 shows the bridge design using partial bridge or complete bridge design for power conversion. These designs are common in power electronics for efficiently managing power flow and voltage regulation. Magnetic Link and AC Generation, Inductive charging operates based on a magnetic link between coils (loops), which generates alternating current (AC). This AC is essential for transferring power wirelessly from the charging station (transmitter) to the vehicle (receiver). Separate Control Converters: The system requires separate control converters for the essential (main power transfer) and non-essential (auxiliary or secondary functions) sides of the charging process. This segregation helps in managing power flow and optimizing efficiency. Dual-Stage Design, Typically, inductive charging systems use a dual-stage design involving AC-DC and DC-AC converters. This setup facilitates the conversion of power from the grid (AC) to high-frequency AC for IPT. Compensation Networks, To mitigate losses and improve efficiency, parallel and series compensation networks are utilized. These networks help in managing reactive power and optimizing the overall power factor of the charging system. Research Focus: Current research is focusing on improving both the primary (main power transfer) and secondary (auxiliary power management) components of the system. This includes reducing losses and enhancing overall efficiency.
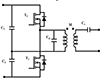 |
Fig. 16 Half bridge DC-AC converter. |
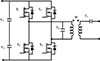 |
Fig. 17 Full bridge DC-AC converter. |
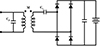 |
Fig. 18 The secondary side AC-DC converter. |
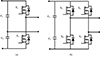 |
Fig. 19 Voltage source inverter topologies. |
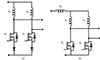 |
Fig. 20 CSI topologies. |
 |
Fig. 21 Transforming to equivalent series Resistor Inductor Capacitor (RLC) circuit. |
 |
Fig. 22 Frequency with inductance. |
 |
Fig. 23 Frequency v/s capacitance. |
The technical intricacies involved in optimizing inductive charging systems for EVs. These systems require sophisticated power electronics and control strategies to maximize efficiency, reduce losses, and improve overall performance, thereby advancing the feasibility and adoption of wireless charging technologies in the automotive industry.
3.1 Primary side DC-AC
Several configurations may be explored, focusing on the initial DC-to-AC conversion and the following AC-to-DC conversion. A passive rectifier with a DC-DC converter or an active AC-DC network connects the secondary source side to the load side battery on the auxiliary plane 7. The main side generally chooses a half bridge or full bridge converter design to increase power quality. This study uses a full bridge current-fed converter to boost voltage transmission.
3.2 Secondary side AC-DC
An optional AC-DC converter converts IPT AC electricity to DC voltage for battery charging. AC-DC systems use passive or active rectifiers for efficiency and control. Utility meets power factor to load total harmonic distortion with AC/DC converter. The compensation network receives high-frequency voltage pulses with variable duty cycles from the stable DC voltage on the primary side. Different compensation networks serve different goals. Optimal power transfer needs load-source impedance matching. From magnetically coupled coils, passive rectifiers convert AC signals with four diodes. DC voltage must be adjusted for battery charging. Controlling separated rectifier-battery charging current requires DC-DC conversion. Figures 24–29 show this solution.
 |
Fig. 24 Simulation model output waveforms are given in the following figures. |
 |
Fig. 25 Complete bridge inverter simulation of 1.6 kW circuit. |
 |
Fig. 26 Simulation voltage across capacitor for 1.6 kW circuit. |
 |
Fig. 27 Inductor voltage simulation for 1.6 kW circuit. |
 |
Fig. 28 1.6 kW circuit input current simulation result. |
 |
Fig. 29 Simulation result of inductor current for 1.6 kW circuit. |
3.3 Classifications based on power converter topologies
IPT inverters use direct current from solar modules or rectified alternating current grids. This converter supplies high-frequency alternating current to the primary resonant tank and controls load power. Literature classifies IPT power converter designs. Configuring Voltage Source Inverters: Toggling two switches usually unbalances the neutral point voltage between two capacitors. The half-bridge architecture is limited to providing AC output with ±vdc/2 amplitude, making it appropriate for lower-power applications. H-bridge converters are practical and recommended in most situations. Figure 24 depicts voltage source inverter architectures.
IPT systems sometimes employ current source inverters (CSI) [5–7]. Figure 19 depicts the current-fed push-pull inverter that powers current IPT systems with parallel Inductor Capacitor (LC) transmitter coil tank networks. The literature describes these systems’ benefits.
Table 3 lists IPT factors.
Parameters simulated converter topologies.
Table 3 displays assessed inductive power transmission parameters. The simulation model and analysis employ the same parameters for voltage-fed and current-fed topologies. Table 2 compares LC values for transmitter-side capacitor voltage stress, transmitting coil voltage stress, transmitter-side capacitor current stress, inverter switches voltage stress, source protection, and coil weight for various frequency range characteristics of IPT topologies. Simulation research computation will be examined.
IPT systems for charging electric cars are being examined. Electrical properties of inductive power transmission are evaluated for current-fed and voltage-fed topologies. The simulation models for performance analysis in Matlab/SIMULINK incorporate these parameters. An extensive comparison of the results and features of both topologies shows that the current-fed topology exhibits better performance because of reduced voltage stress on the transmitting side, voltage stress on the inverter kept within acceptable levels, source protection, and decreased coil weight for inductive wireless power transmission. Designing the receiver coil and operating converters needs accuracy and provides specific problems. The current fed architecture is ideal for IPT in WPT, particularly for charging electric automobiles.
4 Calculation and simulation results
The theoretical main circuit values are calculated using many equations. The main circuit schematic includes a secondary load Rl. Figure 20 shows how connecting the load resistor directly to the primary side skips the transformer to simplify computation. The principal side resistor is Rl.
The primary circuit equations may be obtained from resonant circuit ideas. In a circuit at resonance, the imaginary components of complex impedance or admittance are zero. Calculate the circuit’s total impedance and set the imaginary component to zero to get its resonant frequency (6).
Solve for ω to obtain the following equation.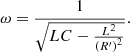 (6)
(6)
The final equation (7) for capacitance is derived from the equation provided previously.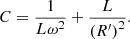 (7)
(7)
To determine the capacitance value, input all variable values into the provided equation. The relationship between voltage and current at resonance is defined by an equation involving the input voltage represented as Vi (8).![$$ {V}_{{in}}=I\left[\frac{{\left({\omega L}\right)}^2{R}^{\prime}{{\left({R}^{\prime}\right)}^2+{\left({\omega L}\right)}^2}\right] $$](/articles/stet/full_html/2024/01/stet20240130/stet20240130-eq8.gif) (8)
(8)
Thus, the voltage drop in the resonant circuit during resonance is purely due to the component of the circuit impedance.
The equation for the input current at resonance is represented by equation (9).![$$ I={V}_{{in}}\left[\frac{{\left({R}^{\prime}\right)}^2+{\left({\omega L}\right)}^2}{{\left({\omega L}\right)}^2{R}^{\prime}\right]. $$](/articles/stet/full_html/2024/01/stet20240130/stet20240130-eq9.gif) (9)
(9)
To find the quality factor of this circuit, transform it into a series RLC circuit as shown in Figure 21.
The quality factor of a series RLC circuit is calculated using equation (10).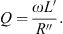 (10)
(10)
By solving the preceding equation, we can derive equation (11) for the quality factor by inserting the formulae for resistance and inductance.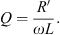 (11)
(11)
The calculation for the Quality factor shown above is given in terms of inductance. Another equation may be formed by utilising the Quality factor and capacitance. The Quality factor of a series RLC circuit may be defined in relation to capacitance as follows.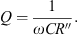
As indicated below, capacitor voltage may be determined. Equation (12) represents capacitor voltage. (12)
(12)
Replace that term with Q to get the capacitor voltage equation,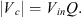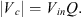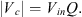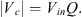 (13)
(13)
To compute inductor voltage, use the following method. Equation (13) states that the inductor and resistor are in parallel when the secondary side resistor is connected to the primary side in the main circuit.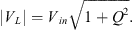 (14)
(14)
The following formula calculates the inductor current.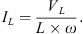 (15)
(15)
Capacitor current equals circuit current. Mathematical calculations for 1.6 kW circuits. The equations from the previous section are used to calculate the circuit. Table 2 lists 1.6 kW system specifications.
Equation (7) represents capacitor voltage.
Substituting Vi = 120 V and Q = 5 yields,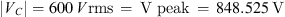
The voltage across the inductor is given by, equation (14)
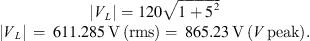
Calculate capacitance using the equation,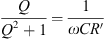 (16)
(16)
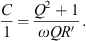 (17)
(17)
Substituting all right-hand numbers in the following equation yields capacitance,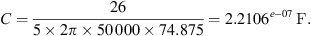
Formula for total circuit current at resonance,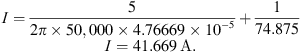
Inductor current is calculated using the formula,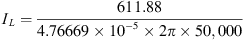
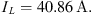
Capacitor current equals circuit input current,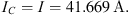
Table 4 summarizes basic circuit model calculations. Frequency affects circuit characteristics Changes in operating or resonance frequency might change circuit properties. Frequency increases circuit compactness, as described in the previous chapter. Excessive frequency ranges may increase system losses. The circuit parameters are calculated for 20 kHz, 30 kHz, and 50 kHz to theoretically analyze the frequency effect. Each frequency value has different inductance and capacitance values. Table 2 lists inductance (L) and capacitance (C) values for different frequencies [34].
L and C values for different frequencies.
Figures 22 and 23 show L and C values changing with operation frequency.
Figures 22 and 23 show frequency-induced L and C decrease. Higher frequencies reduce component values, making systems smaller. This system uses 50 kHz because less frequency increases size. Switching power losses and magnetic fields must be considered while increasing frequencies to minimize system size [33].
Calculating system design ratio Based on system characteristics, find the best turns ratio. The system’s turn ratio is 2.5 based on characteristics and observations. This research shows that fixing this issue raises the ratio to 2.5. This system’s secondary output voltage is 244.7529 V with 2.5 turns. By rectifying the voltage with a DC-DC converter, the secondary side may produce 400 V DC.
To reduce DC-DC power losses, the conversion ratio is set between 0.4 and 0.6. Full-wave rectifiers convert AC power to DC via a higher average DC output voltage than half-wave rectifiers. Calculate turn ratio from system outputs. The system is evaluated at 1, 1.5, 2, and 2.5 turn ratios. Table 5 shows the system’s possible output voltages depending on turns ratios, per specifications [35].
Output voltages for different turns ratios.
5 Simulation results for 1.6 kW system
Figure 24 shows the major circuit architecture simulation. Simulations are done in MATLAB/SIMULINK. The simulation model shows that a PWM generator generates inverter gate signals. The transformer’s primary windings are connected to the resonant inductor, and the inverter’s output powers the circuit. The circuit is simulated using the calculations from earlier sections, and the outputs are compared to the theoretical calculations. Figures 25–30 depict the respective simulations [36].
 |
Fig. 30 Simulation of 1.6 kW secondary winding output voltage. |
Full bridge inverters convert 120 V DC input voltage to 120 V AC voltage (Fig. 18).
Simulated outcomes match theory. Table 6 compares estimated and simulated values.
Compares calculated and obtained values.
A 2.5 turn ratio is used in this simulation model to validate prior work in this journal. Calculated values match simulation findings for all Table 6 system parameters. Simulations validate the 2.5-rotation system concept. Hardware implementation to verify estimates will be explained [36].
6 Experimental and hardware results
System viability depends on hardware implementation. Hardware implementation confirms theoretical findings. The hardware control and driver circuit designs are in the appendix. Before being assembled into a system, the control, driving, and inverter components are built and tested independently. System parameters are tested at each stage to guarantee proper operation. Figure 31 shows the experiment apparatus.
 |
Fig. 31 Hardware setup. |
Hardware testing for the low-power primary circuit model is complete. A low-power circuit is simulated before hardware installation. Tables 7 and 8 list low-power test bed simulation requirements.
Low-power test bed simulation specifications.
Comparison of calculated and simulated low-power test bed values.
UC-3875 Phase Shift Resonant Controller and IR2125 current-limiting single channel driver are used. In actual application, UC 3875’s oscillator can operate at 1 MHz. This controller has beneficial defences. Until the input voltage exceeds 30.75 V, all outputs will be active low. The device can guard against overcurrent by turning off outputs within 70 ns of failure. A 120 V DC power source activates the controller in this thesis. The controller has four outputs, ABCD, with A and C in one phase and B and D in another. The controller signals the IR2125 driving circuits. Each of the four driving circuits sends gate control signals to an inverter switch. The IR2125 is a high-speed MOSFET/IGBT driver with an overcurrent protection circuit. Using a driver circuit protects system hardware. Table 8 criteria establish test bed theoretical values. Low power circuit calculations employ the 1.6 kW model’s system parameter formulae. Table 9 shows all hardware configuration calculated values [35].
Calculated values for the hardware test bed.
Low-power test bed simulations confirm theoretical calculations. The experiment uses the 6.5-W main circuit. Control and driving circuits use 12 V. A 12 V power source supplies the main circuit, and theoretical computations verify outputs. The hardware circuit’s theoretical peak voltages were 84.45 V for the resonant capacitor and 86.53 V for the inductor. Figures 32 and 33 illustrate the hardware experiment resonant inductor and capacitor voltage output waveforms [34].
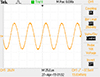 |
Fig. 32 Hardware output for voltage across capacitor without transmission core. |
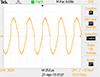 |
Fig. 33 Hardware output for voltage across inductor without transmission core. |
Hardware measurements show peak capacitor and inductor voltages of 68 V and 84 V, respectively, which match theoretical values. The hardware’s capacitors and inductors resonate as predicted, confirming the theory. Using 2.5 and 1 turning ratios, the system is tested with no load, 10%, 30%, and 50% load. Transmission and receiver distances range from 0 cm to 8 cm during the tests. Observations: The experimental setup records output voltage fluctuations with different loads and transmitter-receiver distances. Figure 34 displays load test results and output voltage fluctuations. At various distances, tables and graphs show how transmitter-receiver distance affects output voltage. Waveform analysis shows that V0 and −I0 are almost in phase, indicating a power factor near 1. Only channels If 1 and If 6 are shown due to oscilloscope channel constraints, with approximately equal amplitude and phase angle. Figure 35 shows six load current amplitude changes as load resistance increases. All six resistances match. Coils’ parasitic resistances gradually reduce load current. The computed load currents match the recorded ones. System Efficiency: Figure 36 shows load resistance’s effect on system efficiency. The solid line shows calculated efficiency, whereas the dots show measured values. Efficiency peaks at 86.6% with a normalized load resistance of 0.14. The findings show good efficiency, especially with six loads. Figure 37 shows that the proposed WPT system’s load current is load-independent regardless of load conditions. This shows steady and reliable performance under various load resistances. Table 10 shows the Output voltage values at different distances between transmitter and receiver. Hardware measurements, load tests, waveform analysis, load current variations, and system efficiency prove that the proposed WPT system works. The system is stable and efficient under diverse load conditions since theoretical predictions and actual results correlate well.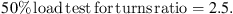
 |
Fig. 34 Experimental load current waveforms. |
 |
Fig. 35 Load current variations against the load resistance. |
 |
Fig. 36 System efficiency against the load resistance. |
 |
Fig. 37 Load currents’ variations against the increasing load resistance (R2 = R4 = R6 = 0; R1, R3, and R5 have the same and varying load resistances). |
Output voltage values at different distances.
Figure 38 represents the data indicating that the system functioned effectively under varying load situations. As the coupling distance increased, the secondary output voltage decreased, yet there was always enough output across the secondary terminals regardless of the load conditions. Verification of Theory and Simulation: The secondary output voltage exhibited minimal decline when the proximity between the main and secondary coils grew and the load was heightened. The low-power circuit simulations and theoretical calculations confirmed that the hardware findings fit with theory and simulation expectations regarding the primary terminals and resonant inductor voltage matching. Increasing the coil distance from 0 cm to 3 cm resulted in a notable decrease in output voltage across all scenarios. Although secondary voltages remained consistently at approximately half of the expected levels, incorporating the hardware test bed on the Printed Circuit Board (PCB) enhanced system output. PCBs were observed to decrease losses and wire degradation, therefore improving overall efficiency. Conclusion: The test of the medium-voltage direct current network for the 1.6 kW IPT system showed that a 2.5 turn-ratio design was effective. The system’s performance was unsatisfactory when the turn ratio was less than 2.5. The method recommended, with a turn ratio of 2.5, was found to be effective for actual applications. The compensating coil in the WPT system plays a dual role by helping achieve a resonant state for improved energy transmission and transmitting energy to the succeeding Inductor Capacitor Capacitor (LCC) circuit through magnetic coupling. The emphasis was on designing the compensating coil utilizing a 3D FEA simulation tool to provide precise performance analysis and system optimization. Tested the proposed WPT system with six distinct loads to verify its functionality under diverse workloads in real-world settings. The capability to provide power to numerous multilayer converter driver circuits suggests extensive use in power electronics for renewable energy and high-voltage power transmission. The study shows that the suggested WPT system is effective under different conditions, confirms theoretical expectations, and indicates practical uses in power electronics, especially for multilayer converters and EV charging systems.
 |
Fig. 38 Plot the relationship between output voltage and distance for a turns ratio of 2.5, at 50% load. |
References
- Semsar S., Luo Z., Nie S., Lehn P.W. (Jan. 2024) Integrated wireless charging receiver for electric vehicles with dual inverter drives, IEEE Trans. Power Electron. 39, 1, 1802–1814. https://doi.org/10.1109/TPEL.2023.3320664. [CrossRef] [Google Scholar]
- Zhang Y., Liu C., Zhou M., Mao X. (2024) A novel asymmetrical quadrupolar coil for interoperability of unipolar, bipolar, and quadrupolar coils in electric vehicle wireless charging systems, IEEE Trans. Ind. Electron. 71, 4, 4300–4303. https://doi.org/10.1109/TIE.2023.3277123. [CrossRef] [Google Scholar]
- Hua Z., Chau K.T., Pang H., Yang T. (Nov. 2023) Dynamic wireless charging for electric vehicles with autonomous frequency control, IEEE Trans. Magn. 59, 11, 8700405. https://doi.org/10.1109/TMAG.2023.3293793. [Google Scholar]
- Banothu C.S., Rao G.S., Vijay Babu A.R. (2023) Magnetic coupling spiral-square coil mutual inductance evaluation for interoperable conditions with different misalignments, in: 2023 3rd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 21–22 December, pp. 1–6. https://doi.org/10.1109/ICEFEET59656.2023.10452230. [Google Scholar]
- Narasipuram R.P., Mopidevi S., Dianov A., Tandon A.S. (2024) Analysis of scalable resonant DC–DC converter using GaN switches for xEV charging stations, World Electr. Veh. J. 15, 218. [CrossRef] [Google Scholar]
- Mahesh A., Chokkalingam B., Mihet-Popa L. (2021) Inductive wireless power transfer charging for electric vehicles – a review, IEEE Access 9, 137667–137713. https://doi.org/10.1109/ACCESS.2021.3116678. [CrossRef] [Google Scholar]
- Zhang Y., Wu Y., Shen Z., Pan W., Wang H., Dong J., Mao X., Liu X. (July 2023) Integration of onboard charger and wireless charging system for electric vehicles with shared coupler, compensation, and rectifier, IEEE Trans. Ind. Electron. 70, 7, 7511–7514. https://doi.org/10.1109/TIE.2022.3204857. [CrossRef] [Google Scholar]
- Zhang S., Yu J.J.Q. (2022) Electric vehicle dynamic wireless charging system: optimal placement and vehicle-to-grid scheduling, IEEE Internet Things J. 9, 8, 6047–6057. https://doi.org/10.1109/JIOT.2021.3109956. [CrossRef] [Google Scholar]
- Elghanam E., Ndiaye M., Hassan M.S., Osman A.H. (2023) Location selection for wireless electric vehicle charging lanes using an integrated TOPSIS and binary goal programming method: a UAE case study, IEEE Access 11, 94521–94535. https://doi.org/10.1109/ACCESS.2023.3308524. [CrossRef] [Google Scholar]
- Mangu B., Kumar K.K., Fernandes B.G. (2011) A novel grid interactive hybrid power supply system for telecom application, in: 2011 Annual IEEE India Conference, Hyderabad, India, 16–18 December, IEEE, pp. 1–5. https://doi.org/10.1109/INDCON.2011.6139543. [Google Scholar]
- Narasipuram R.P., Mopidevi S. (2023) A dual primary side FB DC-DC converter with variable frequency phase shift control strategy for on/off board EV charging applications, in: Proceedings of the 2023 9th IEEE India International Conference on Power Electronics (IICPE), Sonipat, India, 28–30 November, IEEE, PP. 1–5. [Google Scholar]
- Banothu C.S., Gorantla S.R., Attuluri R.V.B., Evuri G.R. (2024) Impacts of wireless charging system for electric vehicles on power grid, e-Prime – Adv. Electr. Eng. Electron. Energy 8, 100561. [CrossRef] [Google Scholar]
- Razu M.R.R., Mahmud S., Uddin M.J., Islam S.S., Bais B., Misran N., Islam M.T. (2021) Wireless charging of electric vehicle while driving, IEEE Access 9, 157973–157983. https://doi.org/10.1109/ACCESS.2021.3130099. [CrossRef] [Google Scholar]
- Ju Y., Liu W., Zhang Z., Zhang R. (2022) Distributed three-phase power flow for AC/DC hybrid networked microgrids considering converter limiting constraints, IEEE Trans. Smart Grid 13, 3, 1691–1708. [CrossRef] [Google Scholar]
- Song J., Mingotti A., Zhang J., Peretto L., Wen H. (2022) Fast iterative-interpolated DFT phasor estimator considering out-of-band interference, IEEE Trans, Instrum. Meas. 71, 1–14. [Google Scholar]
- Ravikiran V., Keshri R.K., Bertoluzzo M. (2018) Efficient wireless charging of batteries with controlled temperature and asymmetrical coil coupling, in: IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December, IEEE, 1–5. [Google Scholar]
- Sun Q., Lyu G., Liu X., Niu F., Gan C. (2024) Virtual current compensation-based quasi-sinusoidal-wave excitation scheme for switched reluctance motor drives, IEEE Trans. Ind. Electron. 71, 9, 10162–10172. [CrossRef] [Google Scholar]
- Bukya R., Mangu B., Jayaprakash A., Ramesh J. (2020) A study on current-fed topology for wireless resonant inductive power transfer battery charging system of electric vehicle, in: 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 28–29 February, pp. 415–421. [Google Scholar]
- Narasipuram R.P., Mopidevi S. (2023) A novel hybrid control strategy and dynamic performance enhancement of a 3.3 kW GaN–HEMT-based iL2C resonant full-bridge DC–DC power converter methodology for electric vehicle charging systems, Energies 16, 5811. [CrossRef] [Google Scholar]
- Wang H., Pratik U., Jovicic A., Hasan N., Pantic Z. (Dec. 2021) Dynamic wireless charging of medium power and speed electric vehicles, IEEE Trans. Veh. Technol. 70, 12, 12552–12566. https://doi.org/10.1109/TVT.2021.3122366. [CrossRef] [Google Scholar]
- Li Y., Sun W., Liu J., Liu Y., Yang X., Li Y., Hu J., He Z. (Nov. 2022) A new magnetic coupler with high rotational misalignment tolerance for unmanned aerial vehicles wireless charging, IEEE Trans. Power Electron. 37, 11, 12986–12991. https://doi.org/10.1109/TPEL.2022.3184335. [CrossRef] [Google Scholar]
- Narasipuram R.P., Mopidevi S. (2024) An industrial design of 400 V–48 V, 98.2% peak efficient charger using E-mode GaN technology with wide operating ranges for xEV applications, Int. J. Numer. Model. Electron. Netw. Devices Fields 37, e3194. [CrossRef] [Google Scholar]
- Bukya R., Mangu B., Bhaskar B., Bhavsingh B. (2021) Analysis of interoperability different compensation network in wireless EV charging systems, in: 2021 2nd Global Conference for Advancement in Technology (GCAT), Bangalore, India, 1–3 October, IEEE, pp. 1–6. https://doi.org/10.1109/GCAT52182.2021.9587618. [Google Scholar]
- Narasipuram R.P., Mopidevi S. (2024) Assessment of E-mode GaN technology, practical power loss, and efficiency modelling of iL2C resonant DC-DC converter for xEV charging applications, J. Energy Storage 91, 112008. [CrossRef] [Google Scholar]
- Yao Y., Gao S., Mai J., Liu X., Zhang X., Xu D. (2022) A novel misalignment tolerant magnetic coupler for electric vehicle wireless charging, IEEE J. Emerging Sel. Top. Ind. Electron. 3, 2, 219–229. https://doi.org/10.1109/JESTIE.2021.3051550. [CrossRef] [Google Scholar]
- Narasipuram R.P., Karkhanis V.A., Ellinger M., Saranath K.M., Alagarsamy G., Jadhav R. (2024) Systems engineering – a key approach to transportation electrification, in: Symposium on International Automotive Technology; SAE Technical Paper, 2024–26-0128, SAE International. [Google Scholar]
- Bukya R., Mangu B., Bhaskar B., Ramesh J. (2022) Design and performance analysis of compensation capacitors in P-S topology for wireless system on receiver side, in: 2022 IEEE 2nd International Conference on Sustainable Energy and Future Electric Transportation (SeFeT), Hyderabad, India, 4–6 August, IEEE, pp. 1–6. https://doi.org/10.1109/SeFeT55524.2022.9909354. [Google Scholar]
- Lu Y., Tan C., Ge W., Zhao Y., Wang G. (2023) Adaptive disturbance observer-based improved super-twisting sliding mode control for electromagnetic direct-drive pump, Smart Mater. Struct. 32, 1, 17001. [Google Scholar]
- Mangu B., Fernandes B.G. (Sept. 2014) Multi-input transformer coupled DC-DC converter for PV-wind based stand-alone single phase power generating system, in: IEEE Energy Conversion Congress and Exposition, ECCE’2014, Pittsburgh, PA, USA, 14–18 September, IEEE, pp. 5288–5295. [Google Scholar]
- Vijay Babu A.R., Kumar P.M., Rao G.S. (2017) Design and modelling of fuel cell powered quadratic Boost converter based multi-level inverter, in: 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April, IEEE, pp. 1–6. [Google Scholar]
- Lei Y., Yanrong C., Hai T., Ren G., Wenhuan W. (2023) DGNet: an adaptive lightweight defect detection model for new energy vehicle battery current collector, IEEE Sens. J. 23, 23, 29815–29830. [CrossRef] [Google Scholar]
- Balu V., Krishnaveni K., Srinivas P. (2022) TSK-fuzzy controllers for novel energy management system of renewable energy sources based AC microgrid with five level inverter, in: 2022 IEEE 10th Power India International Conference (PIICON), New Delhi, India, 25–27 November, IEEE, pp. 1–6. https://doi.org/10.1109/PIICON56320.2022.10045092. [Google Scholar]
- Feng J., Yao Y., Liu Z., Liu Z. (2024) Electric vehicle charging stations’ installing strategies: considering government subsidies, Appl. Energy 370, 123552. [CrossRef] [Google Scholar]
- Banothu C.S., Gorantla S.R., Attuluri R.V.B., Evuri G.R. (2024) Interoperable square-circular coupled coils for wireless electric vehicle battery charging system with different misalignments, IET Power Electron. 1–18. [Google Scholar]
- Vijay Babu A.R., Rajyalakshmi V., Suresh K. (2017) Renewable energy integrated high gain DC-DC converter with multilevel inverter for water pumping applications, J. Adv. Res. Dyn. Control Syst. 9, 1, 172–190. [Google Scholar]
- Anand S., Farswan R.S., Mangu B., Fernandes B.G. (2012) Optimal charging of battery using solar pv in standalone dc system, in: 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, 27-29 March, IET, pp. 1–6. https://doi.org/10.1049/cp.2012.0339. [Google Scholar]
- Patra P., Samanta S., Patra A., Chattopadhyay S. (2006) A novel control technique for single-inductor multiple-output DC-DC buck converters, in: IEEE International Conference on Industrial Technology, Mumbai, India, 15-17 December, IEEE, pp. 807–811. [Google Scholar]
- He T., Zheng Y., Liang X., Li J., Lin L., Zhao W., Li Y., Zhao J. (2023) A highly energy-efficient body-coupled transceiver employing a power-on-demand amplifier, Cyborg Bionic Syst. 4, 30. [CrossRef] [Google Scholar]
- Kurs A., Karalis A., Moffatt R., Joannopoulos J.D., Fisher P., Soljacic M. (2007) Wireless power transfer via strongly coupled magnetic resonances, Science 317, 83–86. [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Basic structure of IPT charging system of EVs. |
| In the text | |
 |
Fig. 2 Transmitter coils used in this research. (a) Spiral circular type coil. (b) Spiral Square type coil. |
| In the text | |
 |
Fig. 3 Photograph of the measured transmitter coil. |
| In the text | |
 |
Fig. 4 Quantified frequency-related transmitter coil inductance and Q-factor. The solid blue line indicates inductance, whereas the dashed red line shows Q-factor [24]. |
| In the text | |
 |
Fig. 5 Displays the inductance and Q-factor of the receiver coil at different frequencies. The solid blue line represents inductance, whereas the dashed red line represents Q-factor. |
| In the text | |
 |
Fig. 6 Interoperable coupling coils. |
| In the text | |
 |
Fig. 7 The coupling coefficient k changes with the height h. The solid blue line represents the observed value, whereas the dashed red line represents the value calculated using equation (3). |
| In the text | |
 |
Fig. 8 A schematic circuit design was utilised to analyse the potential maximum power transfer efficiency. |
| In the text | |
 |
Fig. 9 This investigation’s transmitter and receiver circuit diagram. |
| In the text | |
 |
Fig. 10 Exhibits A’s simulated voltage and current. The dashed red line denotes voltage, whereas the solid blue line shows current. |
| In the text | |
 |
Fig. 11 Simulation of B’s voltage and current. The dashed red line denotes voltage, whereas the solid blue line shows current. |
| In the text | |
 |
Fig. 12 Displays the simulated and actual voltage of the transmitter coil. The solid blue line shows the actual measurement, while the dashed red line indicates the simulated result. |
| In the text | |
 |
Fig. 13 Compares transmitter coil current simulation and measurement. The solid blue line indicates the measured value, while the dashed red line shows the simulation. |
| In the text | |
 |
Fig. 14 Displays simulated and observed receiver coil voltage. The solid blue line indicates the measured value, while the dashed red line shows the simulation. |
| In the text | |
 |
Fig. 15 Displays measured and simulated receiving coil current. The solid blue line shows actual data, whereas the dashed red line models it. |
| In the text | |
 |
Fig. 16 Half bridge DC-AC converter. |
| In the text | |
 |
Fig. 17 Full bridge DC-AC converter. |
| In the text | |
 |
Fig. 18 The secondary side AC-DC converter. |
| In the text | |
 |
Fig. 19 Voltage source inverter topologies. |
| In the text | |
 |
Fig. 20 CSI topologies. |
| In the text | |
 |
Fig. 21 Transforming to equivalent series Resistor Inductor Capacitor (RLC) circuit. |
| In the text | |
 |
Fig. 22 Frequency with inductance. |
| In the text | |
 |
Fig. 23 Frequency v/s capacitance. |
| In the text | |
 |
Fig. 24 Simulation model output waveforms are given in the following figures. |
| In the text | |
 |
Fig. 25 Complete bridge inverter simulation of 1.6 kW circuit. |
| In the text | |
 |
Fig. 26 Simulation voltage across capacitor for 1.6 kW circuit. |
| In the text | |
 |
Fig. 27 Inductor voltage simulation for 1.6 kW circuit. |
| In the text | |
 |
Fig. 28 1.6 kW circuit input current simulation result. |
| In the text | |
 |
Fig. 29 Simulation result of inductor current for 1.6 kW circuit. |
| In the text | |
 |
Fig. 30 Simulation of 1.6 kW secondary winding output voltage. |
| In the text | |
 |
Fig. 31 Hardware setup. |
| In the text | |
 |
Fig. 32 Hardware output for voltage across capacitor without transmission core. |
| In the text | |
 |
Fig. 33 Hardware output for voltage across inductor without transmission core. |
| In the text | |
 |
Fig. 34 Experimental load current waveforms. |
| In the text | |
 |
Fig. 35 Load current variations against the load resistance. |
| In the text | |
 |
Fig. 36 System efficiency against the load resistance. |
| In the text | |
 |
Fig. 37 Load currents’ variations against the increasing load resistance (R2 = R4 = R6 = 0; R1, R3, and R5 have the same and varying load resistances). |
| In the text | |
 |
Fig. 38 Plot the relationship between output voltage and distance for a turns ratio of 2.5, at 50% load. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.