| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 50 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.2516/stet/2024048 | |
| Published online | 14 August 2024 | |
Regular Article
Frequency stability control method for multi-energy system considering storage characteristics and transmission inertia of hot and gas pipeline network
1
School of Electrical Engineering, Shenyang University of Technology, Shenliao West Road No. 111, Shenyang 110870, Liaoning, China
2
Energy Technology Center, Aalborg University, Fredrik Bajers vej 5, Aalborg, DK-9220, Denmark
* Corresponding author: tengyun@sut.edu.cn
Received:
10
May
2024
Accepted:
24
June
2024
The grid-connected capacity of renewable energy generation in multi-energy microgrid is increasing. This leads to a decrease in the inertia level in the microgrid, which has a great impact on the frequency stabilization control. This article proposes an adaptive control method for frequency control of inertia in multi-energy microgrids. Firstly, the system frequency fluctuation problem is addressed. Analyze the response characteristics of virtual inertia and the influence of physical inertia of rotating equipment on system frequency dynamics in multi-energy microgrid. Secondly, study the energy transfer characteristics of electric, thermal and gas systems in multi-energy microgrids. The energy coupling model between the subsystems in the multi-energy microgrid is established. And according to the difference of energy transmission time inertia of electric, heat and gas subsystems, the microgrid inertia response time model of different energy systems is established. Then, according to the energy balance stability criterion of multi-energy microgrid, combined with the current operating state of the system and the state of the higher-level distribution network, the fast response adaptive over-compensation control of multi-energy microgrid cluster is carried out to realize the inertia allocation in multi-energy microgrids. Finally, the proposed advanced frequency control method of multi-energy microgrid considering inertia demand is verified by simulation.
Key words: Inertia / Multi-energy coupling / Energy deficit criterion / Adaptive override control
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
With the development of new power system, the high proportion of power electronic devices is connected to the multi-energy microgrid, which seriously weakens the inertia support and frequency regulation ability of the power system under the same power disturbance. In order to cope with the risks caused by various uncertainties in the multi-energy system and to avoid the system inertia deficiency caused by fault conditions. To improve the level of system frequency stability, there is an urgent need for frequency control of multi-energy microgrids by analyzing the coupling characteristics of energy among energy sources, the inertia time characteristics of energy subsystems, and the relationship between distributed power sources and frequency regulation [1–3].
The current domestic and international research on inertia frequency control strategies for power systems has made certain breakthroughs, but the analysis and summarization of the frequency change characteristics of low-inertia power systems still lacks in-depth and comprehensive elaboration and exploration. In order to solve the problem of frequency fluctuation in multi-energy microgrids, the rate of change of frequency (RoCoF) index is generally used to estimate the critical value of power system inertia. Literature [4] proposes a different calculation method for inertia assessment. The power of each regional contact line after disturbance and the system frequency is utilized to assess the inertia demand of the system online, but the assessment needs to be completed before so that the system frequency safety can be guaranteed. Literature [5–7] obtains the real-time system frequency through dynamic monitoring and assesses the system inertia demand online. Literature [8] obtains the system’s real-time frequency and power values by selecting the appropriate sliding step and utilizes the frequency response equation to obtain the online estimated value of system inertia. Literature [9], considering the inertia support and primary frequency regulation ability of photovoltaic units, a frequency response model of the power system considering the inertia support and primary frequency regulation ability of new energy is established. Literature [10–13], the inertia control model of doubly-fed wind turbine with stator flux oriented vector control is derived. A cooperative control strategy based on virtual inertia control and rotor speed control is proposed. The virtual inertia control module and rotor speed control module are established in Matlab/Simulink.
Literature [14], an adaptive virtual inertia and damping coefficient cooperative control scheme based on virtual synchronous generator (VSG) is proposed. By establishing the mathematical model of VSG, the influence of virtual moment of inertia J and damping coefficient D on the stability of the system is analyzed. The cooperative adaptive control strategy of inertia and damping is obtained by improving the traditional VSG control strategy. The parameters of the adaptive control system are determined. Literature [15] proposed a multi-energy microgrid-based optimal regulation and control method, which analyzed the interconnection relationship between gas, heat, and power grids, and established the nonlinear equations of the gas system, heat system, and power system. The corresponding parameters in the system are obtained by solving the tidal equations of the gas, heat, and power systems, so as to realize the purpose of real-time optimization and control of power among multi-energy microgrids. The above research mainly focuses on the control of the frequency regulation characteristics of the power subsystem after adding clean energy into the multi-energy microgrid or the research on the coordinated and optimized scheduling control of the grid primary frequency regulation and multi-energy microgrid by adding energy storage devices. In order to meet the inertia demand of the multi-energy microgrid system and improve the frequency cooperative support capability of the system, it is necessary to analyze the influencing factors of the inertia demand of the multi-energy microgrid cluster, and to realize the inertia frequency stability of the system through the coordination of multi-energy [16–19].
Current research on frequency control for multi-energy systems. Some references use the energy function method. The energy function method is a method to judge the transient stability of the system directly from the energy point of view without relying on numerical integration. The energy function method is faster than the time domain simulation method and can obtain the stability margin information.
This paper examines the time inertia characteristics of various energy subsystems in a multi-energy microgrid that affect the grid frequency. It then performs dynamic frequency control based on the inertia time characteristics of different energy sources. The first step is to establish a model for the multi-energy microgrid’s inertia demand characteristics. Secondly, we establish the stability criterion for energy supply and demand balance in the multi-energy microgrid by analyzing the real-time state of each energy flow. We then calculate the real-time energy supply satisfaction degree of the system. The system energy demand is quantified by over-assessment using the time scale difference of different energy transmission inertia, and adaptive over-compensation coefficients are preset for the energy balance control of the multi-energy microgrid. The simulation verifies that the multi-energy microgrid can achieve the inertia dynamic frequency control of the system through adaptive overrun control under different fault conditions.
The main research contents of the article are as follows: Section 2 analyzes the inertia demand of multi-energy microgrids. Obtained the effect of transmission time inertia on grid frequency for heat and gas networks in multi-energy microgrids. Section 3 research on adaptive frequency control of multi-energy microgrid. In Section 4, the simulation verification of adaptive control in multi-energy microgrid inertia dynamic frequency control is carried out. Section 5 is the conclusion.
2 Multi-energy microgrid inertia analysis
When the system is disturbed. Taking advantage of the long inertial support time and support capacity of the gas system and the thermal system. Provide power subsystem minute frequency modulation service. The inertia in the multi-energy microgrid mainly contains power-side inertia and load-side inertia. As the inertia in the system is reduced and the inertia distribution is changed, the frequency deviation propagation becomes faster. When the new energy source does not participate in frequency control, the system frequency amplitude becomes larger. If the new energy source participates in frequency control, its output power responds quickly to the frequency change and acts quickly on the generator rotor, which can reduce the frequency amplitude.
When the multi-energy microgrid operates under autonomous conditions, the multi-energy microgrid should be able to cope with the active shocks caused by the interruption of the external contact line through its own regulation, and keep the system frequency change stable within the safe range.
The generalized inertia is composed of rotational inertia and simulated inertia. The rotational inertia includes the rotational inertia of synchronous motor and asynchronous motor. The simulated inertia is the equivalent inertia provided by the power electronic interface device through the improvement of the control strategy. The simulated inertia resources include the following type and the grid type converter resources. The composition of the generalized inertia resource system and the typical equipment of various inertia resources are shown in Figure 1.
 |
Fig. 1 Multi-energy coupling system. |
2.1 Equivalent inertia of power electronics for multi-energy microgrids
The inertia of a multi-energy system is determined by its total rotational kinetic energy. Distributed generators based on non-rotating power electronics will significantly reduce the overall inertia factor of the system. Distributed generators based on non-rotating power electronics will significantly reduce the overall inertia factor of the system due to the widespread use of renewable energy sources. To measure the active regulation capability of the power electronics interface, the existing concept of rotational inertia and primary FM modulation coefficient is generalized [20, 21].
The equivalent inertia of a power electronic device in a multi-energy system represents Je. Compared with the time t = 0–, the energy increment injected by the power electronic equipment into the power grid at time t is equivalent to the energy released by Je. Mass accelerated from the angular frequency ωe(0_) to ωe(t), where ωe is the angular frequency of the rotating magnetic field corresponding to the grid-side current iabc of the converter.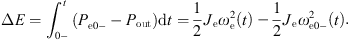 (1)
(1)
The differential equation form of (1) is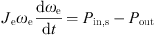 (2)where Pin,s is the set value of the input power of the grid-connected power electronic equipment in the multi-energy microgrid. Pout is the output power value of power electronic equipment in a microgrid.
(2)where Pin,s is the set value of the input power of the grid-connected power electronic equipment in the multi-energy microgrid. Pout is the output power value of power electronic equipment in a microgrid.
The swing equation of a synchronous generator in a power system is: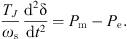 (3)
(3)
The swing equation of synchronous generator in transient process is obtained as follows: (4)TJ is the inertial time constant of the generator set. δ is the rotor angle of the generator. ω is the deviation between the rotor angular velocity and the synchronous angular velocity. ωs is the synchronous angular velocity. H is the inertial time constant. Pm is the mechanical input power of the generator. Pe is the electromagnetic output power of the generator. D is the equivalent damping coefficient. Pe and Ω are the amplitude and disturbance frequency of the periodic disturbance load, respectively.
(4)TJ is the inertial time constant of the generator set. δ is the rotor angle of the generator. ω is the deviation between the rotor angular velocity and the synchronous angular velocity. ωs is the synchronous angular velocity. H is the inertial time constant. Pm is the mechanical input power of the generator. Pe is the electromagnetic output power of the generator. D is the equivalent damping coefficient. Pe and Ω are the amplitude and disturbance frequency of the periodic disturbance load, respectively.
When there is a sudden fluctuation in the load in the power subsystem, the energy demand in the system is expressed as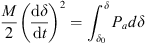 (5)where δ0 is the initial value of generator power angle. δ is the generator power angle after system equilibrium. Pa is the acceleration power of the generator.
(5)where δ0 is the initial value of generator power angle. δ is the generator power angle after system equilibrium. Pa is the acceleration power of the generator.
2.2 Analysis of frequency influences on multi-energy microgrids considering gas grid response
According to the momentum conservation equation of natural gas pipeline, combined with its flow and pressure relationship. Analogous to the power network, the node flow and node pressure functions of the gas pipeline network are obtained. The momentum balance equation is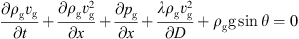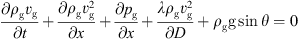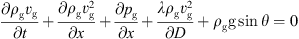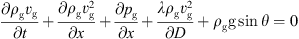 (6)where ρg is the density of the transport medium in the gas network. vg is the flow rate of the medium in the gas network. pg for the gas network pressure. λ for the friction coefficient of the gas network. Usually a function of the gas medium flow rate. D is the diameter of the gas network. θ is the inclination of the pipe network. g is the acceleration of gravity. t, x respectively time and space coordinates.
(6)where ρg is the density of the transport medium in the gas network. vg is the flow rate of the medium in the gas network. pg for the gas network pressure. λ for the friction coefficient of the gas network. Usually a function of the gas medium flow rate. D is the diameter of the gas network. θ is the inclination of the pipe network. g is the acceleration of gravity. t, x respectively time and space coordinates.
Rg = λvg/(AD), Lg =1/A, cg =A/(RT), 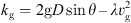 /(2RTD) R and T are the gas constants and temperature of the natural gas, and A is the cross-sectional area of the pipeline. The gas system flow and pressure function model obtained as
/(2RTD) R and T are the gas constants and temperature of the natural gas, and A is the cross-sectional area of the pipeline. The gas system flow and pressure function model obtained as![$$ {G}_l=\left[-\frac{2{Y}_{\mathrm{g}}{p}_0}{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}\mathrm{sin}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)+{G}_0\mathrm{cos}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)+\frac{{k}_{\mathrm{g}}{G}_0}{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}\mathrm{sin}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)\enspace \right]{e}^{-{k}_{\mathrm{g}}l/2} $$](/articles/stet/full_html/2024/01/stet20240129/stet20240129-eq9.gif) (7)
(7)
![$$ {p}_l=\left[{p}_0\mathrm{cos}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)-\frac{2{Z}_{\mathrm{g}}{G}_0}{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}\mathrm{sin}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)-\frac{{k}_{\mathrm{g}}{p}_0}{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}\mathrm{sin}h\left(\frac{\sqrt{{k}_{\mathrm{g}}^2+4{Z}_{\mathrm{g}}{Y}_{\mathrm{g}}}}{2}l\right)\enspace \right]{e}^{-{k}_{\mathrm{g}}l/2} $$](/articles/stet/full_html/2024/01/stet20240129/stet20240129-eq10.gif) (8)where Zg = Rg + jωLg, Yg = jωCg, Gl is the amount of gas flowing out of the end of the gas pipe network. G0 is the amount of gas flowing into the first end of the network. p0 is the pressure at the first end of the pipeline at the pumping station. l is the length of the pipe. h is the vertical height of the pipe.
(8)where Zg = Rg + jωLg, Yg = jωCg, Gl is the amount of gas flowing out of the end of the gas pipe network. G0 is the amount of gas flowing into the first end of the network. p0 is the pressure at the first end of the pipeline at the pumping station. l is the length of the pipe. h is the vertical height of the pipe.
In the gas subsystem, the rotational inertia is mainly provided by the gas turbine, so the gas subsystem fluid inertia model is obtained at different nodes as: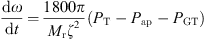 (9)
(9)
![$$ {P}_{\mathrm{ap}}=\sum_{n=1}^n\frac{{p}_0{G}_l\lambda }{\left(\lambda -1\right)}\left[{\left(\frac{{p}_l}{{p}_0}\right)}^{\frac{\lambda -1}{\lambda }}-1\right] $$](/articles/stet/full_html/2024/01/stet20240129/stet20240129-eq12.gif) (10)where λ is the gas compression coefficient. ζ is the compressor pressure ratio. Mr is the moment of inertia. PT is the power of the turbine. Pap is the compressor power consumption in the gas network system. PGT is the gas turbine output power.
(10)where λ is the gas compression coefficient. ζ is the compressor pressure ratio. Mr is the moment of inertia. PT is the power of the turbine. Pap is the compressor power consumption in the gas network system. PGT is the gas turbine output power.
2.3 Response time analysis of multi-energy microgrids considering thermal network inertia
The main indicators to determine the energy balance in the thermal system are the pressure of the pipe network and the temperature of the transmission medium. By calculating the pressure of the heating network and the temperature of the medium, the transmission energy of the heating network system is obtained, and the energy function model of the thermal system is established.
Similar to the energy function of the power network, the momentum conservation equation of the thermodynamic system is established as: (11)where ρh is the density of the transmission medium in the heating network. vh is the velocity of hot medium. D is the diameter of pipe network. ph is the rated pressure of the heat pipe network. λ is the friction coefficient of the pipe network. θ is the inclination angle of the pipe network. g is the acceleration of gravity. t, x denotes time and space respectively.
(11)where ρh is the density of the transmission medium in the heating network. vh is the velocity of hot medium. D is the diameter of pipe network. ph is the rated pressure of the heat pipe network. λ is the friction coefficient of the pipe network. θ is the inclination angle of the pipe network. g is the acceleration of gravity. t, x denotes time and space respectively.
From the above equation, the relationship between the medium flow rate G and the pressure in the system can be obtained. The pressure balance equation of the thermal system is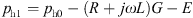 (12)
(12)
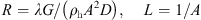 (13)
(13)
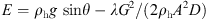 (14)where ph1, ph0 are the pressure at the end and head of the pipeline. A is the cross-sectional area.
(14)where ph1, ph0 are the pressure at the end and head of the pipeline. A is the cross-sectional area.
When the pumping station in the piping system is pressurized, the relationship between the pressure difference A at the two ends of the pipe and the flow rate is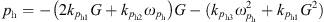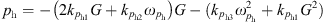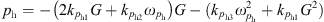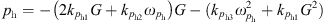 (15)where
(15)where 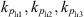 are the intrinsic factor of the pressurized pumping station.
are the intrinsic factor of the pressurized pumping station. 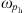 is the rotation frequency of the pressurized pump.
is the rotation frequency of the pressurized pump.
The pressure energy required during medium transfer is expressed as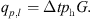 (16)
(16)
By analyzing the pressure energy lost by the transfer of medium flow in the pipe network and the thermal energy transferred. The thermal inertia time in the control process of the thermal subsystem is obtained from the above analysis as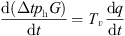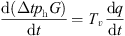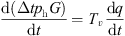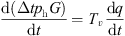 (17)where Tv is the transmission response time constant of the thermal system. q is the medium flow rate in the system.
(17)where Tv is the transmission response time constant of the thermal system. q is the medium flow rate in the system.
3 Adaptive frequency control of multi-energy microgrid
3.1 Multi-energy flow cooperative control mechanism
When analyzing the mechanism of the total energy balance on the power angle change of the power subsystem at a certain time scale in the multi-energy microgrid, divide the energy balance relationship of the multi-energy microgrid into two parts: electric energy balance and non-electric energy balance. At the same time, due to the conversion relationship between electric energy and non-electric energy, such as gas and heat energy, non-electric energy can provide balance support when electric energy is unbalanced at a specific time scale, while electric energy can also provide balance support when non-electric energy is unbalanced.
When the energy balance of a certain energy changes at a specific time scale, it is first judged whether the total energy of the system is balanced. If the total energy of the system is balanced, the energy imbalance support can be provided by the mutual conversion between different energy forms. If the total energy of the system is also unbalanced, it is necessary to increase the energy supply output or reduce the load demand to ensure the energy balance of the system. The control time scale of the power subsystem in the multi-energy microgrid is small, while the energy balance control time scale of the heat and gas system is large. In the case of energy fluctuation of power subsystem, the energy stability control of multi-energy microgrid can be realized by the energy transmission inertia between the pressure energy of the heat and gas subsystem pipe network and the electric energy. Improve the level of grid frequency stability.
3.2 Analysis of adaptive frequency stability control
From the unbalanced power to the system frequency recovery stability. The frequency dynamics of the traditional power system are determined by the kinetic energy increment of the synchronous machine rotor, the unbalanced power, and the rotational inertia. Unbalanced power and rotational inertia determine the frequency acceleration. The increment of rotor kinetic energy further determines the offset of frequency. This mechanism will be promoted in power systems with a large number of power electronic interfaces. The frequency dynamics are determined by the total energy storage increment, unbalanced power, and equivalent inertia of the system.
In the process of energy stability evaluation in multi-energy microgrid. Considering the potential energy at the coupling node of the power subsystem and other energy systems in the multi-energy microgrid, the energy function model is established as follows: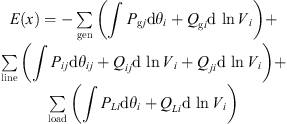 (18)P, Q, V and θ are active power, reactive power, voltage amplitude, and phase angle respectively. Taking P as an example to illustrate the meaning of each subscript. Pgi and Plj are the active power of generator node i and load node j, respectively. Pij is the active power from node i to node j. D is the generator damping. w represents the angular velocity of the generator rotor.
(18)P, Q, V and θ are active power, reactive power, voltage amplitude, and phase angle respectively. Taking P as an example to illustrate the meaning of each subscript. Pgi and Plj are the active power of generator node i and load node j, respectively. Pij is the active power from node i to node j. D is the generator damping. w represents the angular velocity of the generator rotor.
When the energy in the system fluctuates, the deviation the current frequency of the power grid and the rated frequency is Δfnon(t). According to the current frequency of the system, the system power angle δ is![$$ \begin{array}{c}\delta (t)={\delta }_v(t)+\Delta {\delta }_v(t)=2\pi {\int }_0^t\Delta {f}_{\mathrm{non}}(t)\mathrm{d}t+{\delta }_0+\frac{\mathrm{\pi \Delta }{f}_{\mathrm{non}}(t)}{{f}_n}\enspace \\ -\frac{\Delta {f}_{\mathrm{non}}(t)}{\Delta {f}_{\mathrm{non}}(t)+2{f}_n}\mathrm{sin}\left\{2\left[{\int }_0^t2\pi \Delta {f}_{\mathrm{non}}(t)\mathrm{d}t+{\delta }_0\right]\right\}\end{array} $$](/articles/stet/full_html/2024/01/stet20240129/stet20240129-eq23.gif) (19)Δδv is the offset of the system phase angle after frequency offset. fn(t) is the current frequency of system. Set
(19)Δδv is the offset of the system phase angle after frequency offset. fn(t) is the current frequency of system. Set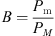 (20)
(20)
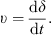 (21)
(21)
Equation (3) can be written as![$$ {M}_1\upsilon \frac{\mathrm{d}\upsilon }{\mathrm{d}\mathrm{\delta }}={P}_M\left[B-\mathrm{sin}\delta \right]. $$](/articles/stet/full_html/2024/01/stet20240129/stet20240129-eq26.gif) (22)
(22)
Integral (19), and take δ = δ0 to δm as the upper and lower limits of the integral, when δ = δ0 · υ = 0.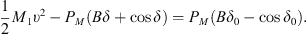 (23)
(23)
Taken H0 = −PM (Bδ + cos δ),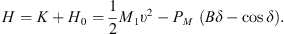 (24)
(24)
When H = H0, the trajectory of (υ, δ) is a phase plane trajectory. The calculation of critical values H, δ of Hc and δc can be expressed by the following formula: (25)
(25)
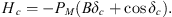 (26)
(26)
The state of energy regulation is set to δ = δ′, υ = υ′. In order to ensure the energy balance of the whole energy system, it is necessary to satisfy that the energy function value H(δ′, υ′) is smaller than the E value.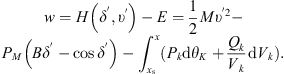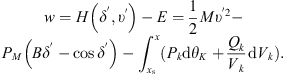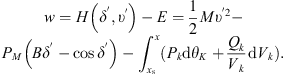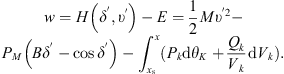 (27)
(27)
When W < 0, the system is stable.
When W = 0, is critical stable state.
When W > 0, is unstable. In the case of unstable system, the system is adjusted in the following steps (Fig. 2):
-
When the multi-energy microgrid is disturbed, the initial inertial response (t0~): the total equivalent inertia of the power supply of the synchronous generator set and the virtual synchronous machine interface determines the initial acceleration of the frequency.
-
When the system frequency fluctuates, the equivalent inertia response (~tp1) is performed by controlling the electronic device: the frequency deviation change rate reaches the threshold, and the power electronic interface power supply with additional inertia provides equivalent inertia to slow down the acceleration of the system frequency drop.
-
When the frequency fluctuation exceeds a certain range, primary frequency modulation (tp1 ~ tp2) is carried out: the frequency drop exceeds the dead zone of primary frequency modulation, and the power supply of the synchronous generator set and VSG set increases output.
-
Frequency secondary drop (tp2~): Since the equivalent inertia of the system is reduced to the minimum at this time, the frequency may decrease rapidly, and the secondary drop extreme value may be smaller than the first drop.
-
Primary frequency recovery frequency: The system frequency is restored to a safe range by increasing the power output in the multi-energy microgrid.
-
Secondary frequency modulation: when the primary frequency modulation makes the adjustment deviation too large, by adjusting the generator output setting value, acting on the unit, wind turbine blade, increasing the generator output of the system, or to a certain extent, according to the heat and gas transmission time inertia to reduce the corresponding load, until the rated frequency of the system is restored.
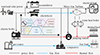 |
Fig. 2 Frequency adjustment of multi-energy system. |
3.3 Adaptive control and parameter adjustment model of multi-energy microgrid
In the process of adaptive parameter cooperative control of inertia frequency of microgrid, the output of new energy in a multi-energy microgrid system has great randomness and volatility, which leads to frequent jitter of system frequency and poses a certain threat to the safe and stable operation of system frequency. In the dynamic control process of multi-energy microgrids, due to the fluctuation of energy supply and demand, it is difficult for the control system to maintain the real-time energy balance of the system under a fixed compensation coefficient. In order to drive the compensation coefficient to change adaptively according to the change of diversity, a compensator that can provide adaptive lead compensation coefficient is designed, which can be expressed by the following function.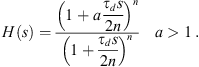 (28)
(28)
The leading angle of formula (28) can be written as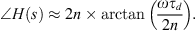 (29)
(29)
The phase of the transfer function of the formula (28) is the same as the phase of 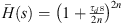 . The corresponding transfer function can be obtained from the reference [22–24] as follows:
. The corresponding transfer function can be obtained from the reference [22–24] as follows: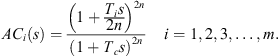 (30)
(30)
As shown in the formula (30), the molecule represents the compensator phase that needs to be regulated in advance. Tc is the time constant related to the system dynamics. The size of the Tc value directly determines the anti-interference ability of the system. If the increase of Tc value increases the gain and phase of the system to a certain extent, the lead compensation of all control loops in the multi-energy microgrid is expressed as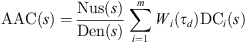 (31)where Wi is the weight factor of the lead compensator DCi, and the root of the molecule is used as the phase of the lead compensation so formula (32) can be obtained.
(31)where Wi is the weight factor of the lead compensator DCi, and the root of the molecule is used as the phase of the lead compensation so formula (32) can be obtained.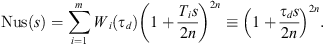 (32)
(32)
In the process of multi-energy microgrid control, increasing the advancer can enhance the accuracy of system compensation, thereby increasing the stability of the system. By matching (31), the weight factors of the coefficients on both sides are obtained, and the following equations are obtained: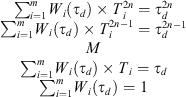 (33)when m = 2n + 1, Wi(τd) can be uniquely obtained by solving the neural network, where Tl and Tm are the minimum and maximum lead times of the control system. Therefore, the lead compensation adaptive control based on the set value considering the demand response is shown in Figure 3.
(33)when m = 2n + 1, Wi(τd) can be uniquely obtained by solving the neural network, where Tl and Tm are the minimum and maximum lead times of the control system. Therefore, the lead compensation adaptive control based on the set value considering the demand response is shown in Figure 3.
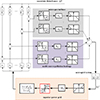 |
Fig. 3 Adaptive leading compensation control of multi-energy system. |
4 Example simulation
In this paper, the simulation uses a 21-node distribution network and a 9-node gas distribution network system in Figure 4. The multi-energy microgrid system includes: a power-to-gas device with a capacity of 0.7 MW; the capacity of each gas turbine is 1 MW, and the maximum transmission capacity of the tie line between the multi-energy microgrid and the upper power grid is 30 MW. The equivalent capacity of the thermal power unit in the upper power grid is 100 MW, and the per-unit value of the adaptive advanced control equivalent frequency modulation parameter is set to M = 6.48, K = 28.12, TR = 6.95, FH = 0.41. The length of a single pipeline of the gas system is 8 km, and the diameter of the pipeline is 0.6 m. The adaptive advance compensation control proposed in this paper is used for example simulation verification.
 |
Fig. 4 Multi-energy coupling system. |
Without considering the hot gas inertia condition in the multi-energy microgrid, the gas turbine can also carry out the active support of the system through its own power output control, while the electric-to-gas device in the system can produce a certain amount of natural gas, which can be regarded as a negative natural gas load. The gas pressure dynamics at each node of the gas distribution network under normal operation and continuous low-frequency/high-frequency perturbation of the multi-energy microgrid is shown in Figure 5, and the light shaded part is the range of fluctuation of the gas pressure at each node, and the upper/lower bounds are the extreme point curves of the gas pressure dynamics under continuous low-frequency/high-frequency perturbation. Under the premise of gas system inertia, the gas pressure at the nodes of the whole gas distribution network is still within a reasonable range through inertia control, which can avoid the unfavorable impact of the gas pressure overrun at the nodes of the gas distribution network caused by the participation of multi-energy microgrids in P-frequency regulation.
 |
Fig. 5 Pressure dynamic curve. |
In the multi-energy microgrid, the inertia level of the power subsystem is affected by the adaptive advance control of heat and gas, thus affecting the power angle oscillation characteristics of the generator in the system. Among them, the inertia time control of hot gas affects the inertia demand of the system, thus affecting the power angle oscillation of the unit. When the electric power shortage, gas load, synchronous machine output, wind power output, and photovoltaic output in the multi-energy microgrid system are shown in Figure 6. In order to analyze the influence of multi-energy microgrid coupling demand response on system frequency stability, the system frequency variation under the coordinated control of electricity, heat, and gas is obtained by analyzing the inertia control of multi-energy microgrid under different scene conditions. The following three scenarios are simulated respectively.
 |
Fig. 6 Load demand and wind power and photovoltaic output. |
Scenario 1: When the renewable energy output in the multi-energy microgrid is reduced at 10 s, and the other energy supply and load demand in the system remain unchanged, the adaptive control method with different lead compensation coefficients is adopted. The lead time is 0s, 20s, and 40s respectively, and the system frequency simulation results are shown in Figure 7. In the case of reduced power supply, by increasing the supply of gas, and through the gas turbine to supply the corresponding power and provide a certain inertia support. The upper system power angle quickly restores stability. When the system fluctuates, the power angle fluctuation of the synchronous generator is compared between the time inertia control considering the multi-energy microgrid and the time inertia control without the multi-energy microgrid as shown in Figure 8.
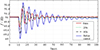 |
Fig. 7 Frequency fluctuation simulation diagram. |
 |
Fig. 8 Power angle fluctuation of synchronous motor. |
Scenario 2: When the gas turbine 3 in the multi-energy microgrid fails at 10 s, the lead time of 0s, 20s and 40s is taken respectively. The system frequency is shown in Figure 9. Due to the large inertia of the gas network, when the system fails, there is no instantaneous large energy fluctuation in the multi-energy microgrid. Through adaptive advance control, under the premise of less gas supply to ensure the pressure of the pipe network, the upper system increases the output power of the synchronous machine. The power transmission capacity of the tie line is increased, and the frequency is restored to be stable. The power angle change is compared with the time inertia control of the microgrid and the time inertia control of the multi-energy microgrid (Fig. 10).
 |
Fig. 9 Frequency fluctuation simulation diagram. |
 |
Fig. 10 Power angle fluctuation of synchronous motor. |
Scenario 3: When the grid node 21 and the gas supply network 7 in the multi-energy microgrid fail at the same time. The lead time was set to 0 ms, 20 s, and 40 s respectively. In order to verify the dynamic performance of the designed control method, a 20% load disturbance is applied to the multi-energy microgrid at t = 30 s, and the system response curve is shown in Figure 11. When the power and gas network in the system fail at the same time, by enabling the energy storage device, under the large time inertia response of the gas system, the frequency fluctuation of the system is obviously reduced after 20 s advanced compensation control. The control system can perform advanced compensation control before the energy of the multi-energy microgrid changes greatly to ensure the stability of the multi-energy microgrid energy. The comparison between the time inertia control considering the multi-energy microgrid and the time inertia control without the multi-energy microgrid is as follows. The power angle of the synchronous generator can be quickly restored to stability by using the method proposed (Fig. 12).
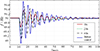 |
Fig. 11 Frequency fluctuation simulation diagram. |
 |
Fig. 12 Power angle fluctuation of synchronous motor. |
Through the analysis of simulation results, the advanced time scale control method of multi-energy microgrid based on energy function is obtained. It can maintain the sum of the electric heating gas energy demand in the system consistent with the sum of the actual control output, and ensure the energy balance. In the process of setting the lead time control, the system control effect is optimal at 20 s. The adaptive advanced energy function control method can improve the minimum power angle oscillation of the system.
Through multi-scenario simulation, in the case of system disturbance or failure. Through the advanced control method based on energy flow, the transmission and transformation of energy can be reasonably controlled according to the renewable energy output and load power in the system. The coordination of the heat and gas network in the system and the traditional power supply in the region participates in the stability balance control, so as to suppress the influence of system disturbance and fault on the system stability.
The analysis of the frequency curve in Figure 13 shows that the inertia demand of the multi-energy microgrid system increases with the extension of the response time of the gas network adjustment power in the system. When the power adjustment time of the gas network in the multi-energy microgrid exceeds 1 min, the inertia demand of the multi-energy microgrid system is greater than the inertia reserve inside the system. The danger of active power imbalance caused by expected faults cannot be solved by putting more inertia levels into operation alone. If the gas network load can respond quickly after receiving the control signal within a period of time before the system fluctuation, the power adjustment task can be completed. The inertia demand in multi-energy microgrids is greatly reduced. The heat network gas network in the multi-energy microgrid system based on advanced control completes power adjustment within a reasonable time. When the inertia time is equal to 2 ~ 5min, the quasi-steady-state frequency of the system is low. At this time, it can be considered to increase the proportional coefficient of the inertia control of the gas network, so as to improve the quasi-steady-state frequency of the system.
 |
Fig. 13 Influence of power adjustment speed of heat and gas network on frequency change. |
5 Conclusion
-
Aiming at the problem of inertia reduction and frequency stability control difficulty in multi-energy microgrids. In this paper, a generalized inertia model in a multi-energy microgrid is established. The classification of inertia in multi-energy microgrid is analyzed. Combined with the difference in energy transmission time scale of different energy subsystems, the energy function of a multi-energy microgrid is established to analyze the system frequency stability process, and the source of inertia energy in a multi-energy microgrid is obtained. Provide sufficient energy support for the power system to maintain system frequency stability.
-
Aiming at the different characteristics of transmission time scales of the power grid, heating network, and gas network in multi-energy microgrids. Through the short-term storage and pressure adjustment method of the pipe network system. The advanced control coefficient is set to realize the power balance of the multi-energy microgrid in a short time and maintain the frequency stability of the system. In the advanced control method of casting in this paper. When the lead time is set to 20 s, the system stability is the best.
-
In order to maintain the stability of the system frequency in the multi-energy microgrid, there is a shortage of inertia level and active power in the system when the multi-energy microgrid fails. The control time scale of the hot gas system is obtained by calculating the allowed latest intervention time of the primary frequency modulation. The simulation results show that the stable control of the system power angle can be effectively realized by adaptive advance control.
Acknowledgments
This work was supported by the National Key Research and Development Program of China under Grant No.2017YFB0902100.
References
- Antalem D.T., Muneer V., Bhattacharya A. (2022) Decentralized control of islanding/grid-connected hybrid DC/AC microgrid using interlinking converters, Sci. Technol. Energy Transition 77, 22. [CrossRef] [Google Scholar]
- Li J., Liu J., Yan P., Li X., Zhou G., Yu D. (2021) Operation optimization of integrated energy system under a renewable energy dominated future scene considering both independence and benefit: a review, Energies 14, 1103. [CrossRef] [Google Scholar]
- Yilmaz M., ElShatshat R. (2023) Zone-oriented 2-stage distributed voltage control algorithm for active distribution networks, Electr. Power Syst. Res. 217, 109127. [CrossRef] [Google Scholar]
- Yan Z.M., Xu Y. (2019) Data-driven load frequency control for stochastic power systems: a deep reinforcement learning method with continuous action search, IEEE Trans. Power Syst. 34, 2, 1653–1656. [Google Scholar]
- Bonfiglio A., Lodi M., Rosini A., Oliveri A., Procopio R. (2024) Design, realization and testing of a synthetic inertia controller for wind turbine power generators, Sustain. Energy Grids Net. 38, 101234. [CrossRef] [Google Scholar]
- Wang Z., Li Z., Zeng X., Yu K., He S., Li J., Lan Y., Zhuo C. (2023) Flexible grounding control strategy based on proportional series inertial control for distribution networks, Electr. Power Syst. Res. 225, 109841. [CrossRef] [Google Scholar]
- Ren M., Sun X., Sun Y., Shi K., Xu P. (2023) A virtual inertial control strategy for bidirectional interface converters in hybrid microgrid, Int. J. Elec. Power Energy Syst. 153, 109388. [CrossRef] [Google Scholar]
- Liu H., Di P., Zhao T., Li H., Liu P. (2023) Adaptive inertia control of hybrid energy storage system based on Butterworth filter, Energy Rep. 9, S7, 288–298. [CrossRef] [Google Scholar]
- Saleh A., Hasanien H.M., Turky R., Turdybek B., Alharbi M., Jurado F., Omran W.A. (2023) Optimal model predictive control for virtual inertia control of autonomous microgrids, Sustainability 15, 6, 5009. [CrossRef] [MathSciNet] [Google Scholar]
- Chen C.Y., Cui M.J., Li F.X., Yin S., Wang X. (2021) Model-free emergency frequency control based on reinforcement learning, IEEE Trans. Ind. Inform. 5, 17, 2336–2346. [CrossRef] [Google Scholar]
- Zhang Y., Zhu H., Wang X. (2019) Prediction for the maximum frequency deviation of post-disturbance based on the deep belief network, in: IEEE Innovative Smart Grid Technologies – Asia (ISGT Asia), Chengdu, China, May 21–24, IEEE, pp. 683–688. [Google Scholar]
- Wang S., Li B., Li G., Yao B., Wu J. (2021) Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration, Appl. Energy 292, 116851. [CrossRef] [Google Scholar]
- Tang X., Wu M., Li M., Ding B. (2022) On designing the event-triggered multistep model predictive control for nonlinear system over networks with packet dropouts and cyber attacks, IEEE Trans. Cybern. 52, 10, 11200–11212. [CrossRef] [PubMed] [Google Scholar]
- Amirrezai M., Rezaie H., Goetz S.M. (2023) Feasibility study of incorporating static compensators in distribution networks containing distributed generation considering system power factor, Electr. Power Syst. Res. 219, 109253. [CrossRef] [Google Scholar]
- Wang Y., Delille G., Bayem H., Guillaud X., Francois B. (2013) High wind power penetration in isolated power systems: assessment of wind inertial and primary frequency responses, IEEE Trans. Power Syst. 28, 3, 2412–2420. [CrossRef] [Google Scholar]
- Fang Y., Hu P., Zhu N., Minfu A., Jiang D. (2024) Sizing method of a novel hybrid energy storage considering adaptive inertia control, Sustain. Energy Technol. Assess. 61, 103602. [Google Scholar]
- Kim J.Y., Kang Y.C., Kim K.H., Kim T.K., Cho D.H., Song S.H., Kim S.C. (2022) Linear control gain for synthetic inertia of a PMSG-based wind turbine generator, J. Electr. Eng. Technol. 18, 1, 53–60. [Google Scholar]
- Song W., Wang L., Zhao W., Zhang X., Wang Z. (2022) Inertia optimization control and transient stability analysis of wind power grid-connected system, Front. Energy Res. 10, 939468. [CrossRef] [Google Scholar]
- Zhang J., Li F., Chen T., Cao Y., Wang D., Gao X. (2022) Virtual inertia control parameter regulator of doubly fed induction generator based on direct heuristic dynamic programming, Energy Rep. 8, S10, 259–266. [Google Scholar]
- Moon Y.H., Cho B.H., Lee Y.H., Hong H.S. (1999) Energy conservation law and its application for the direct energy method of power system stability, in: Proceedings of the 1999 Winter Meeting of IEEE Power Engineering Society. Part 1 (of 2), IEEE, pp. 695–700. [Google Scholar]
- Oludamilare B.A., Ryuto S., Kazuki O., Tomonobu S., Abdul M.H. (2019) Static voltage stability improvement with battery energy storage considering optimal control of active and reactive power injection, Electr. Power Syst. Res. 172, 303–312. [CrossRef] [Google Scholar]
- Liu Z., Wen F., Ledwich G. (2011) Optimal siting and sizing of distributed generators in distribution systems considering uncertainties, IEEE Trans. Power Deliv. 26, 4, 2541–2551. [CrossRef] [Google Scholar]
- Wogrin S., Tejada-Arango D., Delikaraoglou S., Botterud A. (2020) Assessing the impact of inertia and reactive power constraints in generation expansion planning, Appl. Energy 280, 115925. [CrossRef] [Google Scholar]
- Amirrezai M., Rezaie H., Goetz S.M. (2023) Feasibility study of incorporating static compensators in distribution networks containing distributed generation considering system power factor, Electr. Power Syst. Res. 219, 109253. [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Multi-energy coupling system. |
| In the text | |
 |
Fig. 2 Frequency adjustment of multi-energy system. |
| In the text | |
 |
Fig. 3 Adaptive leading compensation control of multi-energy system. |
| In the text | |
 |
Fig. 4 Multi-energy coupling system. |
| In the text | |
 |
Fig. 5 Pressure dynamic curve. |
| In the text | |
 |
Fig. 6 Load demand and wind power and photovoltaic output. |
| In the text | |
 |
Fig. 7 Frequency fluctuation simulation diagram. |
| In the text | |
 |
Fig. 8 Power angle fluctuation of synchronous motor. |
| In the text | |
 |
Fig. 9 Frequency fluctuation simulation diagram. |
| In the text | |
 |
Fig. 10 Power angle fluctuation of synchronous motor. |
| In the text | |
 |
Fig. 11 Frequency fluctuation simulation diagram. |
| In the text | |
 |
Fig. 12 Power angle fluctuation of synchronous motor. |
| In the text | |
 |
Fig. 13 Influence of power adjustment speed of heat and gas network on frequency change. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




