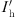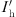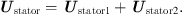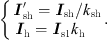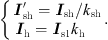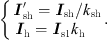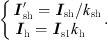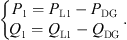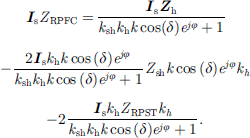| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Decarbonizing Energy Systems: Smart Grid and Renewable Technologies
|
|
|---|---|---|
| Article Number | 51 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.2516/stet/2024042 | |
| Published online | 13 August 2024 | |
Regular Article
Research on the multi-scenario control strategy of an active distribution network based on Rotary Power Flow controller
1
Power Science Research Institute of State Grid Jiangsu Electric Power Co. Ltd., Jiangsu Electric Power Company, Beijing West Road, Gulou District, Nanjing City, Jiangsu Province 210024, China
2
State Grid Jiangsu Electric Power Co. Ltd., 215 Shanghai Road, Gulou District, Nanjing City, Jiangsu Province 210024, China
* Corresponding author: venus1350053@163.com
Received:
29
January
2024
Accepted:
5
June
2024
Aiming at the problems of complex power distribution and difficult adjustment in the active power distribution network, a low-cost, harmonic-free, and low-loss electromagnetic Rotating Power Flow Controller (RPFC) scheme is proposed. First, the topology, working principle, and equivalent circuit of RPFC are introduced, the steady-state characteristics of RPFC are studied, and a steady-state voltage source model containing RPFC lines is established. On this basis, in order to solve problems such as voltage over the limit, phase angle difference, line flexible closed-loop closing, and power control in the active distribution network, an RPFC rotor angle solution strategy based on the improved Multi-Scenario Adaptive Genetic Algorithm (MAGA) was proposed. Taking the actual network as a case, a specific algorithm model was established based on Matlab/Simulink, and compared with the RPFC system under traditional PI control. The results show that using MAGA as the control algorithm enables RPFC to have better performance in voltage regulation and power flow control scenarios. In the voltage regulation scenario, MAGA-RPFC saves 1.5 s of regulation time compared with traditional PI-RPFC. In the power control scenario, the adjustment time is saved by 18.2 s. At the same time, the simulation results show that RPFC can effectively solve the voltage regulation, flexible closed-loop, and power regulation problems in active distribution networks, and has broad application prospects.
Key words: Electromagnetic rotary power controller / Active distribution network / Improved multi-scenario adaptive genetic algorithm / Voltage/power control
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
RPFC: Rotating power flow controller
MAGA: Multi-scenario adaptive genetic algorithm
FACTS: Flexible AC transmission systems
UPFC: Unified power flow controller
DPFC: Distributed power flow controller
HUPFC: Hybrid unified power flow controller
RPST: Rotating phase shifting transformer
Tsh, Th: Shunt transformer, series transformer
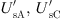 :
Voltage of the shunt transformer
:
Voltage of the shunt transformer
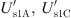 :
Voltage of the series transformer
:
Voltage of the series transformer
Is: Sending bus current of RPFC
Ish: Primary-side current of shunt transformer
Zs: Primary impedance of transformer
Zsh: Secondary impedance of transformer
R1 + jX1, R2 + jX2: Line impedance of bus
R, L: Resistance and inductance of RPFC
URPFCd, URPFCq: d-axis and q-axis components of the RPFC output voltage
Zh: Impedance of series transformer
Ksh: Shunt transformer’s ratio
Ustator1, Ustator2: Stator voltages of the two RPSTs
ZRPFC: RPFC equivalent impedance
PDG, QDG: Distributed photovoltaic power
R0 + jX0: Equivalent impedance of the line
P1 + jQ1, P2 + jQ2: Transmission power of the line
Im: Closing loop point current
SPRPFC: Actual rotational speed of the rotary phase transformer
Pc, Pm: Current values of the crossover and mutation operators
N: Number of generations of the current run
Imax: Maximum current value allowed to pass through the line
Pref, Qref: Set value of transmission power
G, B: Conductance and conductivity in the nodal conductivity matrix
SPRPFCmax: Limiting rotational speed of the rotary phase transformer
Pc0, Pm0: Initial values of the crossover and mutation operators
1 Introduction
Green and low-carbon transformation and response to climate change have become world trends and popular aspirations. Clean power sources and loads such as wind power, photovoltaics, energy storage, and electric vehicles will be widely connected to urban distribution grids [1]. Due to the simple grid structure and relatively single control method of the traditional distribution network, it has exposed some problems of its own when faced with diversified sources and loads, such as difficulty in meeting the development needs of regional balance and exacerbating the distribution network voltage and the complexity of power and difficulty of regulation [2]. In response to the main problems faced by the safe operation of active distribution networks, including voltage limit violations [3], dual power supply phase angle difference line closing, and power flow out-of-control phenomena [4], researchers in related fields have proposed many solutions.
In terms of voltage regulation, existing research can be divided into voltage regulation solutions for On-Load Tap Changer (OLTC) [5] and regulation of Distribution Network Synchronous Compensators (DSTATCOM) pressure scheme [6], voltage regulation scheme involving energy storage [7], etc. Literature [8] studied the impact of OLTC dynamic adjustment on voltage stability. The changes in primary voltage and current before and after OLTC dynamic adjustment can be used to monitor the mid-and long-term stability of the voltage, which can improve the voltage safety and stability of the power system. Literature [9] proposed a control strategy for DSTATCOM to participate in automatic voltage control, which coordinates control with remote control signals in constant reactive power mode, steady-state voltage regulation control mode, and transient voltage control mode. Through its reactive power output Control is carried out to support the access point voltage. However, the resistance voltage drop dominates the low-voltage distribution network, so the reactive power voltage regulation method has certain limitations. Literature [10] proposes a control method for distributed energy storage cluster voltage regulation. By constructing a cluster economic voltage regulation model, the optimal timing output of each cluster’s energy storage is determined. The results show that the proposed method can effectively eliminate node voltage deviations.
In terms of flexible loop closing of phase angle difference lines, literature [11] proposes a scheme that combines series phase-shifting transformers (static compensation) and four-quadrant converters (dynamic compensation). In the static compensation link, by adjusting the transformer winding ratio, the combination method generates the voltage vector to be compensated. In the dynamic compensation link, the output voltage amplitude and phase of the four-quadrant converter are flexibly controlled to achieve real-time online voltage compensation. However, due to the limitations of the design structure, the phase-shifting transformer can only cope with the loop closing situation of 30 phase angle differences, which has certain limitations and brings problems such as complex control and high cost to the operation of power electronic equipment in the dynamic compensation link. Literature [12] proposed a phase shifting scheme of Two Core Symmetrical Phase Shifting Transformer (TCPST). By changing the tap position of the secondary winding of the excitation transformer, the voltage amplitude can be kept unchanged. It realizes the function of voltage phase shifting, but it is an on-load tap changer type phase shifter, so it has the disadvantages of slow adjustment speed, discrete adjustment, and short service life.
In terms of power control, intelligent soft switches have better adjustment functions. Its basic structure consists of high-power fully controlled power electronic components [13]. By applying control strategies to the inverters on both sides, the output voltage amplitude of the access point is satisfied and independent control of the phase to achieve bidirectional decoupling control of active and reactive power flowing through interconnected lines. However, the design capacity of the back-to-back intelligent soft switch is determined by the maximum power that the line needs to transfer, so it exhibits large capacity and low cost. Disadvantages of height and large size.
In the 1990s, the General Electric Company of the United States proposed a flexible AC transmission device-RPFC based on traditional transformers and a Rotary Phase Shifting Transformer (RPST) [22], which can flexibly control the line compensation voltage without being affected by the line current influence, thereby providing a new method for economical, flexible, and frequent control of power systems [14]. At present, most research at home and abroad focuses on RPFC steady-state modelling [15] and power flow control of transmission lines [16]. Literature [17] compared the working characteristics of RPFC and unified power flow controller in transmission network power flow control, pointing out that RPFC has great advantages in terms of operation and maintenance, impact resistance, and cost. However, there are few studies on the application of RPFC in low-voltage distribution networks. This is because the traditional distribution network is based on a one-way power distribution network between the power grid and users. Its operation and control mode is relatively passive, and the demand for power flow control is relatively low. Small [18], and with access to large-scale distributed power sources and the continuous development of intelligent motor production and digital control technology [19], RPFC has re-entered people’s field of vision. Literature [20] proposed a phasor synthesis control and loss reduction optimization strategy based on RPFC, which can optimize line losses while satisfying the voltage quality of the station area. Literature [21] proposed a power-voltage-angle three-closed-loop power decoupling control method based on RPFC, which can effectively control the power at the loop closing point of the interconnected distribution network. However, the existing RPFC system is greatly affected by the parameters of the PI controller, so it is urgent to improve the RPFC system with new algorithms to meet the rapid adjustment requirements. Literature [21] proposed the use of variable universe fuzzy PI control to improve the RPFC controller, which effectively improved the response speed and control accuracy. However, its overshoot phenomenon still has a certain impact on the RPFC adjustment speed and the RPFC response. The improvement of speed has now become the main problem faced by the promotion and application of RPFC. Therefore, further research on RPFC control strategies is urgently needed to give full play to the regulatory performance of RPFC in voltage regulation, phase angle difference line flexible loop closing, and power flow control.
Based on the existing literature research results, this article proposes a solution using RPFC for typical application scenarios in active distribution network construction. First, the RPFC topology and working principle are explained, and a simplified circuit voltage source model of RPFC is established. By changing the RPFC parameters, a voltage vector of any size and direction that can be continuously adjusted in the line can be connected. Furthermore, a voltage over-limit control model based on RPFC, a flexible loop closing model for phase angle difference lines, and a power decoupling control model based on instantaneous reactive power theory were constructed. Then, an RPFC system control strategy using MAGA is proposed, which can directly solve the two rotor angles based on the built multi-scenario model, and output the solution results to the servo motor for real-time control of the RPFC. Finally, a simulation model was built and compared with traditional PI-RPFC. The simulation results showed that MAGA-RPFC significantly improved the system operating speed. Relevant research on RPFC is of great significance for improving the carrying capacity and reliability of distributed energy in distribution networks and is an effective supplementary solution for the construction of new active distribution networks in the future.
2 RPFC topology and working principle
2.1 RPFC topology
In the 1990s, General Electric Company of the United States proposed a flexible AC transmission device based on traditional transformers and rotary phase shifting transformers (Rotary Phase Shifting Transformer, RPST) – electromagnetic rotary power controller (Rotary Power Flow Controller, RPFC), which can flexibly control the line compensation voltage without the influence of line current, thus providing a new method for the economic and flexible control of the power system.
An RPFC topology is shown in Figure 1a, where Tsh is a shunt transformer; Th is a series transformer; RPST1 and RPST2 are spin-transfer phase transformers; and α1 and α2 are the rotor angles of the two spin-transfer phase transformers, respectively.
The rotary phase transfer transformer is the core component of the RPFC, and its working principle is shown in Figure 1b, based on the principle of electromagnetic induction, using two groups of RPST rotor angle rotation, respectively, to synthesize a stator voltage phase with constant amplitude and adjustable phase angle of 360°, and the two voltage phases are superimposed and connected to the secondary side of the series transformer, to inject a series voltage with adjustable amplitude and phase angle in the line.
RPST at rest is similar to a transformer, its stator-side voltage and rotor-side voltage there is a certain ratio relationship, while the phase difference is related to the angle between the stator and rotor α1 and α2, for the multi-pole RPST, the rotor angle only needs to be moved to a very small mechanical angle, you can change the voltage phase quantity of the series into the line.
2.2 Working principle
The operating principle of RPFC is shown in Figure 2a, where 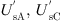 are the secondary side voltages of the shunt transformer Tsh and
are the secondary side voltages of the shunt transformer Tsh and 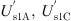 are the secondary side voltages of the series transformer Th.
are the secondary side voltages of the series transformer Th.
 |
Figure 2 Working principle of RPFC. (a) RPFC equivalent circuit diagrams (b) RPFC simplified circuit diagram. |
The single-phase equivalent circuit of RPFC is shown in Figure 2b, where Is is the sending bus current of RPFC; Is1 is the system line current; Ish is the primary-side current of shunt transformer; Zs is the primary-side impedance of shunt transformer; Zsh is the impedance of shunt transformer’s secondary-side; ZRPST is the impedance of rotary transfer phase transformer imputed to the secondary-side; Zh is the impedance of series transformer imputed to the primary-side, and ksh is the shunt transformer’s ratio; 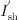 is the RPST rotor current;
is the RPST rotor current; 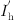 is the stator-side current; Urotor is the rotor-side voltage; Ustator1 and Ustator2 are the stator voltages of the two RPSTs, respectively; and α1 and α2 are the phase-shift angles of the stator and rotor voltages of the two RPSTs, respectively.
is the stator-side current; Urotor is the rotor-side voltage; Ustator1 and Ustator2 are the stator voltages of the two RPSTs, respectively; and α1 and α2 are the phase-shift angles of the stator and rotor voltages of the two RPSTs, respectively.
Neglecting the transformer excitation current, the following relationship can be obtained according to the traditional transformer analysis methods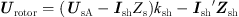 (1)
(1)
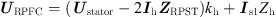 (2)
(2)
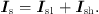 (3)
(3)
Referring to Figure 2a, the stator and rotor voltages of the two RPSTs satisfy the following relationship (5)
(5)
Let δ = (α1 − α1)/2, φ = (α1 + α1)/2, be obtained according to (4) and (5):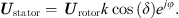 (6)
(6)
Based on the electromagnetic induction theorem, assuming an ideal RPST, there is the active and reactive power emitted or absorbed on the parallel side of the RPST is equal to the active and reactive power absorbed or emitted on the series side, so there is: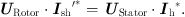 (7)
(7)
Based on (3), (6)–(8) can be calculated to obtain the relationship between the system line current, RPFC stator-side current, RPFC rotor-side current, shunt transformer primary-side current and the RPFC feeder bus current as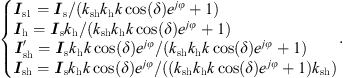 (9)
(9)
Based on (1)–(2) the injection voltage of RPFC can be calculated as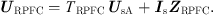 (10)
(10)
Among them, the expressions and derivation process of TRPFC and ZRPFC are shown in Appendix A, so that the simplified circuit model of RPFC can be obtained as shown in Figure 2b, whose series part consists of a controlled ideal voltage source and a variable internal impedance, and the parallel branch is a controlled current source.
According to the RPFC regulation characteristics, it is known that the continuous regulation of the injected line voltage can be accomplished by changing the sizes of α1 and α2, thus realising the functions of voltage regulation, phase angle regulation, power control, etc., as shown in Figure 3 for the RPFC line regulation vector diagram.
 |
Figure 3 Line regulation vector diagram of RPFC. (a) Voltage over the lower limit (b) Voltage over the upper limit (c) Power regulation (reactive) (d) Power regulation (active) (e) Phase angle difference line closing loop. |
3 Multi-scenario analysis and modelling of active distribution networks
Three scenarios are analysed and modelled for the active distribution network construction, as shown in Figure 4, in which K1 is the bus switch of bus 1; K2 is the liaison switch of bus 1 and bus 2; K3 is the liaison switch of bus 2 and bus 3; Us1 is the first-end voltage of bus 1; U1, U2, and U3 are the voltage of the grid-connection point of bus 1, bus 2, and bus 3, respectively; PL and QL are loads of the bus, and PDG and QDG are the power issued by the distributed photovoltaic power of bus 1.
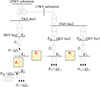 |
Figure 4 Schematic diagram of active distribution grid. |
Scenario 1: Voltage overrun at the end of the line due to power back-feeding caused by a high percentage of distributed PV access (K1).
Scenario 2: Due to factors such as grid layout design, the feeder end of the 35 kV substation comes from the medium-voltage side of the 110 kV substation (triangular connection) and the high-voltage side of the 220 kV substation (star connection), and at this time, there is a phenomenon of a phase angle difference of about 30° between bus 1 and bus 2 (K2); or due to the asynchrony of the line construction and the development of loads, the phase angle difference between the two ends of the merging loop point exists or due to unsynchronised line construction and load development. At this time, the loop-forming operation will generate a large loop current in the line, affecting the security of the power supply in the distribution network.
Scenario 3: For long-term closed-loop operation lines, when effective power control at the closed-loop point is necessary to ensure reliable operation of the distribution network (K3).
3.1 Scenario 1: Control model construction
Referring to Figure 5 Feeder 1, when the PV power P is larger and cannot all be consumed locally, the power will be sent backwards to the grid side through the line, and when P1R + Q1X < 0, the voltage at the end of the line is higher than the grid-side bus voltage, and with the gradual increase of the proportion of photovoltaic access, there is even a phenomenon of voltage over the upper limit, and at this time, the line voltage relationship can be expressed as follows: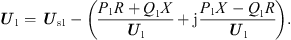 (11)
(11)
 |
Figure 5 Equivalent circuit diagram of closed-loop grid with RPFC. |
Analysing equation (11) and ignoring the less influential imaginary part, the voltage drop ∆U between Us1 and Us can then be expressed as: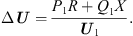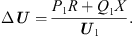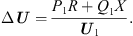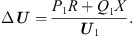 (13)
(13)
When RPFC is connected to K1, the system voltage drop can be expressed as: (14)
(14)
At this point, the voltage at the grid point and the regulation target for scenario 1 can be expressed respectively: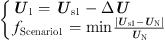 (15)where UN is the nominal system voltage.
(15)where UN is the nominal system voltage.
3.2 Scenario 2: Control model construction
As shown in Figure 5 for a phase angle difference line flexible closed-loop equivalent circuit including RPFC, R0 + jX0 is the equivalent impedance of the outer port of the closed-loop line; R1 + jX1, R2 + jX2 are the line impedance of bus 1 and bus 2, respectively; P1 + jQ1, P2 + jQ2 are the transmission power of the two lines, respectively; URPFC and ZRPFC is the voltage vector of the line into which RPFC is connected in series and the impedance inside RPFC, respectively; U1 and U2 are the voltages of both terminals of RPFC, respectively; and Ksc and Kbp are the series closure switches and parallel bypass switch of RPFC, respectively.
Under the premise that the line parameters within the actual loop closing path, the feeder load before loop closing, and the phase angle difference between the voltages on both sides of the loop closing switch are known, the steady-state loop closing current including RPFC is calculated, and therefore the regulation objective of Scenario 2 (i.e., for the minimum loop closing current) can be expressed as follows: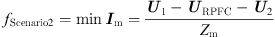 (16)where Im is the steady state combined loop current after adding RPFC and Zm is the total loop impedance, where:
(16)where Im is the steady state combined loop current after adding RPFC and Zm is the total loop impedance, where: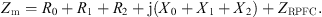 (17)
(17)
3.3 Scenario 3: Control model construction
Referring to Figure 4, the power control model of the K3 closing loop point including RPFC is analysed, and its equivalent circuit is the same as that of Figure 5, under the single-phase coordinate system, it can be obtained that there exists the following relationship between the circuit equations on both sides of the closing loop point: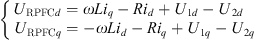 (18)where R and L are the equivalent resistance and inductance of the ZRPFC, so that U1 is fixed on the d-axis as the reference voltage, then we have U1d = U1 and U1q = 0. At this time, the d-axis component and the q-axis component of the line current are:
(18)where R and L are the equivalent resistance and inductance of the ZRPFC, so that U1 is fixed on the d-axis as the reference voltage, then we have U1d = U1 and U1q = 0. At this time, the d-axis component and the q-axis component of the line current are: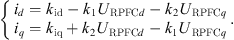 (19)
(19)
The expressions for k1, k2, kid and kiq are given in equation (A5) in Appendix A. In the dq coordinate system, the line power at U1 in Figure 4 can be calculated from the instantaneous power theory [16] as follows: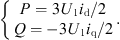 (20)
(20)
Based on equations (19) and (20) after simplified calculation the relationship between URPFCq, URPFCd and the line transmitted power P, Q can be obtained as: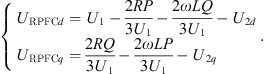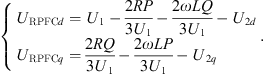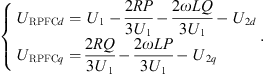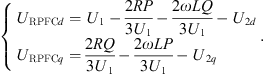 (21)
(21)
At this point, the scenario three objective functions can be expressed as: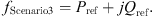 (22)
(22)
In the formula, Pref, Qref for the line set transmission power, at this time the joint formula (21), formula (22) can be obtained URPFC series into the line voltage vector amplitude and angle.
3.4 Restrictive condition
3.4.1 Voltage deviation constraints
According to the “power quality power supply voltage deviation” (GB/T 12325-2008) [23], different voltage levels of the line are allowed to pass through the voltage deviation limit is different, to the voltage deviation limit for voltage constraints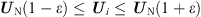 (23)where ε is the voltage deviation rate limit for the specific voltage level.
(23)where ε is the voltage deviation rate limit for the specific voltage level.
3.4.2 Combined loop current constraint
In order to prevent the line current-carrying capacity from crossing the limit for a long period of time during regulation, or from excessive inrush currents due to loop closure leading to equipment burnout or failure, the line current-carrying capacity is constrained as: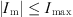 (24)where Im is the closing loop point current on the line and Imax is the maximum current value allowed to pass through the line.
(24)where Im is the closing loop point current on the line and Imax is the maximum current value allowed to pass through the line.
3.4.3 Power equation constraints
The equation constraints confirmed by the power equation during distribution network operation are: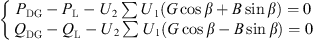 (25)where G and B are the conductance and conductivity in the nodal conductivity matrix and the other parameters have been described above.
(25)where G and B are the conductance and conductivity in the nodal conductivity matrix and the other parameters have been described above.
3.4.4 Control precision constraints
According to the operating characteristics of the RPFC, the control accuracy of the two sets of rotary transfer phase transformers is constrained due to the fact that the servomotor controlling the rotor angle rotation belongs to a kind of mechanical regulation, and there is a deviation of other factors such as inertia: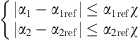 (26)where, α1 and α2 are the actual angles of the two rotary phase transformers, a1ref and a2ref are the control angles of the two rotary phase transformers, and χ is the permissible error of the rotation angle.
(26)where, α1 and α2 are the actual angles of the two rotary phase transformers, a1ref and a2ref are the control angles of the two rotary phase transformers, and χ is the permissible error of the rotation angle.
3.4.5 Motor speed constraint
Since the rotor angular rotation of the RPFC is a type of operation by means of servomotor drive, there is a constraint on the speed of rotor regulation in the RPFC: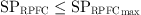 (27)where SPRPFC is the actual rotational speed of the rotary phase transformer and SPRPFCmax is the limiting rotational speed of the rotary phase transformer.
(27)where SPRPFC is the actual rotational speed of the rotary phase transformer and SPRPFCmax is the limiting rotational speed of the rotary phase transformer.
3.4.6 Cycle time constraint
In the power control condition and voltage regulation condition, the design is that the system collects system parameters every η seconds for calculation, so there are: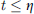 (28)where t is the system computation time.
(28)where t is the system computation time.
3.5 Multi-scene adaptive genetic algorithm solution
According to the principle of the MAGA algorithm and the multi-scene control model of this paper [24], the specific solution steps are as follows:
1) Coding and parameter initialisation. According to the regulation characteristics of the RPFC, its main control parameter is the rotation angle of the two rotary transfer phasor transformers, because the binary coding needs frequent encoding and decoding, which requires a lot of calculations, the real number coding method is used for the solution, which is able to save the solution time, at this time, the corresponding coding of the RPFC can be expressed as [α1, α2]. When the control precision c = 0.0001, it satisfies α1, α2 ∈ [0.0000, 360.0000].
2) Operation scenario discrimination. Since the RPFC in this paper needs to adapt to different application scenarios, i.e., multiple control objectives. In order to overcome the defects of traditional genetic algorithms that is easy to fall into the local optimal solution under the constraints of multi-scene and multi-objective, we complete the operation scene discrimination through the real-time collection of the distribution system parameters and set the initial value of the crossover and variance parameters of different scenarios for the searching need to satisfy the adaptability of the algorithm to different scenarios.
3) Adaptation calculation. Judge whether the results of the control model satisfy the various constraints under the multi-scene control objective [25], due to the fact that the models of each group have been normalised, if a constraint is not satisfied, the individual fitness function is 1. If they are all satisfied, the fitness value is calculated according to the fitness function of the scenario and the optimal individual fitness in the N population is introduced into the N + 1 population, at the same time, the individuals with fitness of non-1 in the population form the mating pool.
4) Selection of action. Form a roulette wheel according to the size of the fitness of the individuals in the mating pool, the greater the fitness, the greater the chance of being selected, using roulette to randomly select the parents and mothers.
5) Crossover variation action. By using automatically varying crossover probability and mutation probability to control the genetic operation, when the search for the optimal stagnation, increase the mutation probability and crossover probability to help jump out of the limitation solution, easy to find the optimal solution, the specific adaptive mechanism can be expressed as: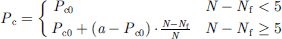 (29)
(29)
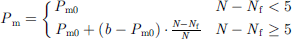 (30)where Pc and Pm are the current values of the crossover and mutation operators, respectively, Pc0 and Pm0 are the initial values, a ∈ [0, Pc], b ∈ [Pm, 0.1], N is the number of generations of the current run, and Nf is the number of generations when there is a stagnation in the algorithm’s optimisation process.
(30)where Pc and Pm are the current values of the crossover and mutation operators, respectively, Pc0 and Pm0 are the initial values, a ∈ [0, Pc], b ∈ [Pm, 0.1], N is the number of generations of the current run, and Nf is the number of generations when there is a stagnation in the algorithm’s optimisation process.
It can be seen that when other parameters are unchanged, the values of the crossover operator Pc and the mutation operator Pm increase with the increase of N under certain conditions, i.e., when the number of times that the optimal solution remains unchanged exceeds a certain value, the algorithm automatically increases the probability of the crossover and the mutation to jump out of the locally optimal solution, and in this paper, the overall control block diagram of the MAGA-RPFC system is shown in Figure 6, and the flowchart of the improved adaptive genetic algorithm is Figure 7 shown.
 |
Figure 6 Overall control block diagram of MAGA-RPFC system |
 |
Figure 7 Algorithm flow chart. |
 |
Figure 8 Simulation results of voltage regulation condition. (a) Two control strategies for pressure regulation process (b) Rotor Angle change process of two control strategies. |
 |
Figure 9 Flexible loop simulation results. |
 |
Figure 10 Simulation results of RPFC regulation when the set power is 0. (a) RPFC control process when the set power is 0 (b) Rotor angle regulation process of RPFC. |
 |
Figure 11 The set value changed from 0 to 1 MW in the regulation process. (a) RPFC control process when the set power is 1 MW. (b) Rotor angle regulation process of RPFC. |
4 Simulation of an algorithm
According to Figure 4 to build the distribution network structure for simulation and analysis, for the multi-scenario adaptive genetic algorithm proposed in this paper, compared with a PI-RPFC approach, the PI-RPFC control strategy is shown in Figure B1–B3 in Appendix B, the RPFC parameters are shown in Table 1, and the parameters of the improved adaptive genetic algorithm for the three working conditions are shown in Table 2.
Major parameters of the 6MW-RPFC system.
MAGA parameters under three working conditions.
4.1 Simulation verification of voltage regulation working conditions
With the increasing number of distributed PV access [26], there has been a daytime power back-feeding caused by the voltage overrun condition, according to Figure 4 grid topology, RPFC access position is K1, access mode refer to Figure 5. When the line end voltage is located in the normal range, the bypass switch Kbp is in the closed state, at this time the RPFC short-circuit access to the line; the voltage overrun phenomenon occurs after the closure of the Ksc after the disconnection of the Kbp After the RPFC is involved in regulation, the distribution network system parameters are shown in Table 3.
System parameters of high-proportion photovoltaic access to distribution grid.
As shown in Figure 8a for the voltage change at the end of the line when the RPFC is put into operation under the two control strategies, it can be seen that the PI-RPFC exhibits a kind of overshooting characteristic, while the MAGA-RPFC, after a short time of computation (the average computation time for the voltage regulation is 0.11 s, which can be neglected in relation to the overall RPFC regulation time), always regulates the voltage at a kind of rated motor speed, so the MAGA-RPFC shows better control accuracy under the same time, the simulation results are shown in Table 1, and the voltage regulation process is shown in Figure 8b.
4.2 Phase angle difference line flexible closed loop working condition simulation verification
As shown in Figure 4, there exists a 30° phase angle difference between the two ends of the K2 switch, when the distribution line is undergoing reconstruction or overhaul, the power supply to the customer will be interrupted if the power failure is used to transfer the load, however, the direct closing of the line with a 30° phase angle difference will lead to a large closing current, which will lead to the action or damage of the protection equipment, therefore, it is necessary to guarantee the power supply to the customer load in an uninterruptible and flexible way, and the access position of RPFC is at the K2 switch in Figure 4, and the access method is referred to Figure 5. The RPFC is connected to the K2 switch in Figure 4, and the access method is referred to in Figure 5. Under normal power supply conditions, the series switch Ksc and the bypass switch Kbp are in the disconnected state, and when the demand for flexible loop closure is raised, the RPFC completes the preparatory work and then Ksc closes, and the system parameters are shown in Table 4.
Phase angle difference line system parameters.
For phase angle difference line flexible loop closing, the system does not have too high requirements for regulation time, after the demand for loop closing transferring power supply is put forward, RPFC parameter calculations are carried out, and the current changes after loop closing are shown in Figure 9, which shows that the RPFC under the two control strategies shows consistency in loop current suppression of loop closing, and the regulation accuracy of the two control strategies is 0.81%.
4.3 Simulation analysis of power control operating conditions
As shown in Figure 4, in which the K3 switch is closed, effective power control is required at the closed loop point under the long-term closed-loop operation condition. At this time, the access mode of RPFC at the K3 switch refers to Figure 5, and the system parameters are shown in Table 5.
Power control system parameters.
In the power control simulation verification, the following experiments are carried out for verification:
-
Before the moment t = 0 s: the series switch Ksc and the bypass switch Kbp are in the disconnected state; and
-
t = 0 s moment: series switch Ksc and bypass switch Kbp are directly closed, at this time, U2 line flows 0.1865 MW active and 0.3309 MVar reactive power to U3 line through bypass switch Kbp, which puts forward the power control demand to the RPFC, and the bypass switch Kbp is disconnected, meanwhile, making the power flow in the closed-loop point to be 0. The power control effect under the two control strategies and corresponding changes of RPFC parameters under the two control strategies are shown in Figure 10a, the comparison of simulation results is shown in Table 6, and the simulation regulation process is shown in Figure 10b;
-
t = 60 s: the power control demand is put forward to RPFC, so that U3 line flows 1 MW active power and 0MVar reactive power to U2 line, at this time, the power regulation effect and the corresponding RPFC parameter changes are shown in Figure 11a, under two power regulation conditions, the average calculation time of MAGA-RPFC is 0.16 s, which can be ignored compared with the overall regulation time of RPFC. The comparison of simulation results at this time is shown in Table 6, and the simulation regulation process is shown in Figure 11b.
RPFC power regulation capability when the set power is 0 or 1.
From the simulation results, it can be seen that the RPFC system based on the improved adaptive genetic algorithm exhibits better regulation performance under the three working conditions, and shows faster response speed and control accuracy compared with the RPFC under PI control, which verifies the feasibility and effectiveness of the proposed control strategy.
5 Conclusion
In view of the problems of voltage regulation, flexible loop closing and power regulation encountered in the construction of active distribution networks, a solution of electromagnetic rotating power controller is proposed. Through theoretical analysis and simulation verification, the following conclusions are drawn:
-
The main structure of RPFC is two sets of phase-shifting transformers. By changing the relative angle of the stator and rotor, the continuous adjustment of the injected line voltage is completed. It is an electromagnetic power flow controller, so it has low cost, no harmonics and high reliability. Advantage. Based on the analysis of the working principle and equivalent characteristics of RPFC, a line steady-state voltage source model was established.
-
For different operating scenarios, a voltage over-limit control model based on the RPFC steady-state voltage source, a flexible loop closing model based on the vector synthesis principle, and a power decoupling model based on the instantaneous reactive power theory were constructed, and the MAGA algorithm was used to The multi-scenario control model was solved, and the simulation results verified the effectiveness of the proposed control strategy.
-
Comparing the control performance of PI-RPFC and MAGA-RPFC algorithms, the RPFC system based on MAGA shows better control effects in terms of control accuracy, response time and adjustment stability.
-
In the face of complex active distribution network multi-operation scenarios, the control target can be achieved simply by switching the RPFC control model, which shows good applicability and generalizability, and has certain implications for future active distribution network construction.
This article proposes a multi-scenario solution based on RPFC, but currently, there are certain limitations in its applicable working conditions. With the rapid development of microgrid construction, in the microgrid quasi-synchronous and interconnected operation scenario, compared with the distribution network interconnection power control scenario, the frequency adjustment dimension of RPFC has been added. Therefore, it is necessary to carry out research on quasi-synchronous control of microgrids based on RPFC.
Acknowledgments
This work was done by the Jiangsu Electric Power Co., LTD. Science and technology project (J2022061).
References
- Yang B., Wei Y., Zeng Q., Xu J., Zhang F., Huang M. (2021) Research on system-friendly optical storage DC microgrid sending-out control strategy via MMC, in: 11th International Conference on Power and Energy Systems (ICPES), IEEE, pp. 501–505. [Google Scholar]
- Huang Y., Söder L. (2017) Assessing the impact of incentive regulation on distribution network investment considering distributed generation integration, Int. J. Elec. Power Energy Syst. 89, 126–135. [CrossRef] [Google Scholar]
- Kuihua W., Jian W., Can C., Liang F., Yang Y., Rong L., Bo Y. (2018) Research on voltage stability of active distribution network with distributed generations, in: 2018 China International Conference on Electricity Distribution (CICED), IEEE, pp. 78–83. [CrossRef] [Google Scholar]
- Li S., Wang T. (2023) UPFC setting to avoid active power flow loop considering wind power uncertainty, Front. Energy 17, 1, 165–175. [CrossRef] [Google Scholar]
- Han L., Yin J., Wu L., Sun L., Wei T. (2022) Research on the novel flexible on-load voltage regulator transformer and voltage stability analysis, Energies 15, 17, 6189. [CrossRef] [Google Scholar]
- Duarte S.N., Almeida P.M., Barbosa P.G. (2021) Voltage compensation in multi-grounded distribution network with a three-phase five-wire DSTATCOM, Electr. Pow. Syst. Res. 197, 107310. [CrossRef] [Google Scholar]
- Zhao H., Hong M., Lin W., Loparo K.A. (2017) Voltage and frequency regulation of microgrid with battery energy storage systems, IEEE Trans. Smart Grid 10, 1, 414–424. [Google Scholar]
- Jundong D., Zhu S. (2011) The effect of OLTC on static voltage stability limit, in: 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, IEEE, pp. 1–4. [Google Scholar]
- Xiong Z., Yuhong W., Gang Z., Hui Y., Ninghui Z., Qingqing Z. (2018) Research and design of distributed static synchronous series compensator, in: 2018 8th International Conference on Power and Energy Systems (ICPES), Colombo, Sri Lanka, IEEE, pp. 263–267. [CrossRef] [Google Scholar]
- Xiang Y., Lu Y., Liu J. (2023) Deep reinforcement learning based topology-aware voltage regulation of distribution networks with distributed energy storage, Appl. Energy 332, 120510. [CrossRef] [Google Scholar]
- Wang C., Wang H., Zhang T. (2024) Hybrid four-quadrant DC–DC converter for DC wind farm collection systems, J. Power Electron. 24, 42–54. [CrossRef] [Google Scholar]
- Liang G.S., Wang L.T., Gao F., Liu X. (2018) A new maximum step voltage calculation method of on-load tap-changer for symmetrical two-core phase-shifting transformer, IEEE Trans. Power Deliv. 33, 6, 2718–2725. [CrossRef] [Google Scholar]
- Li Y. (2019) High power density and high efficiency DC-DC converters based on wide bandgap semiconductors, PhD Thesis, North Dakota State University. [Google Scholar]
- Long Y. (2021) Voltage regulation for distribution networks with smart photovoltaic inverters, PhD Thesis, University of Washington. [Google Scholar]
- Tan Z.L., Zhang C.P., Jiang Q.R. (2015) Research on characteristics and power flow control strategy of rotary power flow controller, in: 2015 5th International Youth Conference on Energy (IYCE), Pisa, Italy, IEEE, pp. 1–8. [Google Scholar]
- Sen D., Acharjee P. (2019) Optimal line flows based on voltage profile, power loss, cost and conductor temperature using coordinated controlled UPFC, IET Gener. Transm. Dis. 13, 7, 1132–1144. [CrossRef] [Google Scholar]
- Tan Z., Chunpeng Z., Qirong J. (2015) Research on characteristics and power flow control strategy of rotary power flow controller, in: 2015 5th International Youth Conference on Energy (IYCE), Pisa, Italy, IEEE, pp. 1, 1–8. [Google Scholar]
- Ba A.O., Peng T., Lefebvre S. (2008) Rotary power flow controller performance in power systems part I – RPFC modeling, in: 2008 IEEE International Symposium on Industrial Electronics, IEEE, pp. 1469–1475. [CrossRef] [Google Scholar]
- Peng T., Ba A.O., Lefebvre S. (2008) Rotary power flow controller performance in power systems part II RPFC performances in a transmission corridor, in: 2008 IEEE International Symposium on Industrial Electronics, IEEE, pp. 1476–1482. [CrossRef] [Google Scholar]
- Haddadi A.M., Kazemi A. (2011) Optimal power flow control by rotary power flow controller, Adv. Electr. Comp. Eng. 11, 2, 79–86. [CrossRef] [Google Scholar]
- Yan X., Shao C., Jia J., Aslam W., Peng W., Yang R. (2023) An accurate power control strategy for electromagnetic rotary power controllers, IET Gener. Transm. Dis. 17, 15, 3524–3540. [CrossRef] [Google Scholar]
- Larsen E.V. (1998) Power flow control with rotary transformers. US Patent 5841267. Available at https://patents.google.com/patent/US5841267A/en [Google Scholar]
- IEC 60038:2014 Safety of machinery – safety-related parts of control systems – part 1: general principles for design and application. Available at https://en.wikipedia.org/wiki/IEC_60038 [Google Scholar]
- Abdulwahid A.H. (2023) Artificial intelligence-based control techniques for HVDC systems, Emerg. Sci. J. 7, 2, 643–653. [CrossRef] [Google Scholar]
- Fikri E., Sulistiawan I.A., Riyanto A., Saputra A.E. (2023) Neutralization of acidity (pH) and reduction of total suspended solids (TSS) by solar-powered electrocoagulation system, Civ. Eng. J. 9, 5, 1160–1172. [CrossRef] [Google Scholar]
- Widjaja R.G., Asrol M., Agustono I., Djuana E., Harito C., Elwirehardja G.N., Pardamean B., Gunawan F.E., Pasang T., Speaks D., Hossain E., Budiman A.S. (2023) State of charge estimation of lead acid battery using neural network for advanced renewable energy systems, Emerg. Sci. J. 7, 3, 691–703. [CrossRef] [Google Scholar]
Appendix A
RPFC steady state voltage source model
It can be obtained from Figure 2
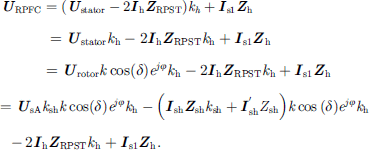 (A1)
(A1)
Based on equation (10) it can be obtained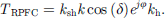 (A2)
(A2)
At this point, we can get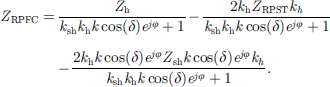 (A4)
(A4)
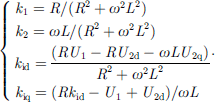 (A5)
(A5)
Appendix B
Traditional RPFC control strategy based on PI control
 |
Figure B1 Voltage regulation flow chart of PI-RPFC. |
 |
Figure B2 Flexible loop closing flow chart of PI-RPFC. |
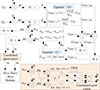 |
Figure B3 Flow control flowchart for PI-RPFC. |
All Tables
All Figures
 |
Figure 1 RPFC topology structure. (a) RPFC schematic [18]. (b) RPFC topology diagram. |
| In the text | |
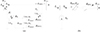 |
Figure 2 Working principle of RPFC. (a) RPFC equivalent circuit diagrams (b) RPFC simplified circuit diagram. |
| In the text | |
 |
Figure 3 Line regulation vector diagram of RPFC. (a) Voltage over the lower limit (b) Voltage over the upper limit (c) Power regulation (reactive) (d) Power regulation (active) (e) Phase angle difference line closing loop. |
| In the text | |
 |
Figure 4 Schematic diagram of active distribution grid. |
| In the text | |
 |
Figure 5 Equivalent circuit diagram of closed-loop grid with RPFC. |
| In the text | |
 |
Figure 6 Overall control block diagram of MAGA-RPFC system |
| In the text | |
 |
Figure 7 Algorithm flow chart. |
| In the text | |
 |
Figure 8 Simulation results of voltage regulation condition. (a) Two control strategies for pressure regulation process (b) Rotor Angle change process of two control strategies. |
| In the text | |
 |
Figure 9 Flexible loop simulation results. |
| In the text | |
 |
Figure 10 Simulation results of RPFC regulation when the set power is 0. (a) RPFC control process when the set power is 0 (b) Rotor angle regulation process of RPFC. |
| In the text | |
 |
Figure 11 The set value changed from 0 to 1 MW in the regulation process. (a) RPFC control process when the set power is 1 MW. (b) Rotor angle regulation process of RPFC. |
| In the text | |
 |
Figure B1 Voltage regulation flow chart of PI-RPFC. |
| In the text | |
 |
Figure B2 Flexible loop closing flow chart of PI-RPFC. |
| In the text | |
 |
Figure B3 Flow control flowchart for PI-RPFC. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.