| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Emerging Advances in Hybrid Renewable Energy Systems and Integration
|
|
|---|---|---|
| Article Number | 80 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.2516/stet/2024045 | |
| Published online | 10 October 2024 | |
Regular Article
The optimal dispatching strategy of cogeneration based on Deep Q-Network (DQN) algorithm
1
School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510000, Guangdong, China
2
Guangdong DangTec Industrial Technology Co., Ltd., Guangzhou 510000, Guangdong, China
* Corresponding author: 1122201051@mail2.gdut.edu.cn; pei_zhang67@outlook.com
Received:
13
April
2024
Accepted:
11
June
2024
This work expands on previous research to offer a state-of-the-art approach for optimizing the dispatching of cogeneration systems, given the limitations faced by conventional coal-fired cogeneration units and the increasing environmental standards. Acknowledging the constraints of flexibility in winter heating, the study aims to improve unit coal use optimization and lower emissions. The paper presents a novel optimization approach for distributing electricity and heat in cogeneration units, utilizing the Deep Q-Network (DQN) algorithm. The suggested approach reduces operating expenses and improves system dependability using a sixth-order function fitting and fuzzy set space division. The study’s results indicate a significant 8.96% increase in performance, demonstrating the effectiveness of the DQN-based strategy in enabling cost-effective scheduling in cogeneration systems. This research offers a road towards sustainable and effective energy use and contributes to the development of cogeneration technology. It also has potential applications in natural energy systems.
Key words: DQN algorithm optimization / Cogeneration / Optimize scheduling / Backbone particle swarm / CHP system / Intelligent sports environment system
Publisher note: This article type has been corrected as Regular Article on 10 January 2025.
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
At present, energy shortage, environmental pollution, and climate change have become the main problems faced by countries all over the world, which have seriously restricted the economic development of countries, damaged people’s health, and caused huge losses. Global energy, environmental, and climate change concerns require international agreements and cooperation. They create a climate of trust and accountability for long-term solutions by encouraging collaboration, setting shared objectives, and information exchange. The sustainable development of a country depends on its resource endowment, agricultural production, and other factors. Infrastructural, educational, healthcare, innovative, governmental, social inclusion, environmental protection, and private sector development are all critical components of sustainable development. Human capital, economic progress, and social well-being are all enhanced by investing in these areas. The primary energy reserves, such as oil, coal, and natural gas, are limited and non-renewable [1]. According to the current energy consumption rate, conventional global fossil energy will be exhausted by the end of this century. Oil, coal, and natural gas can only be supplied for 40, 155, and 65 years. Per capita electricity consumption has improved a society’s living conditions, industrial output, and living standards [2]. Many studies show that the greenhouse gases produced by burning these fuels, such as carbon dioxide and sulfur dioxide, are the main reasons for global warming and the frequent occurrence of extreme El Ni ñ o phenomena. Combining heat and power, or cogeneration, maximizes energy efficiency, minimizes primary energy consumption, prevents grid losses, integrates with renewable energy sources, and improves energy security and resilience to significantly lower greenhouse gas emissions and support environmental sustainability. CHP production technology produces heat and electricity with a single fuel source, considerably reducing greenhouse gas emissions and energy conservation. Emissions, waste heat recovery, and fuel usage are all decreased. In addition to lowering energy consumption and emissions, CHP systems are integrated with demand-side energy efficiency strategies. To solve these problems and the development dilemma, save energy, reduce emissions, and implement a sustainable development strategy. These are the problems that people in all countries need to solve [3].
Cogeneration (CHP for short) is a technology that can produce heat and electricity simultaneously and significantly improve energy utilization efficiency [4]. In the power generation process of ordinary thermal power units, a large amount of waste heat is recycled and discharged into the air after the high-grade steam works on the turbine. Currently, the efficiency of the most advanced combined cycle generator unit is only 40–50%. Cogeneration dispatching efficiency is increased by sophisticated control and monitoring systems that optimize operation according to market pricing, heat load, demand, and fuel supply. They make demand response programs, load tracking, peak shaving, predictive maintenance, and remote monitoring possible. The cogeneration unit, under the same fuel consumption, realizes the cascade utilization of energy, provides the same amount of power products, collects and uses the waste heat in the power generation process, and provides hot water and heating for industry and families, with the overall efficiency of up to 90%. In addition, heat and power cogeneration units generally have large boiler capacity, high flue gas return, and high dust removal efficiency, which are conducive to desulfurization and denitrification in the furnace, with obvious economic and environmental benefits [5]. Combined heat and power generation technology is an effective way to achieve efficient energy utilization at this stage. Advanced forecasting and optimization algorithms are essential for combined heat and power production systems to be integrated into grid operations and to provide accurate projections of energy supply and demand, efficiency, and grid stability. It has shown significant advantages in energy conservation and emission reduction. It is not a new technology, but the development of thermal power units accompanies it, and technology continues progressing. Actively developing cogeneration is an important measure to save energy and reduce environmental pollution, and an inevitable choice for China to build an environment-friendly and resource-conserving society and achieve sustainable development and industrial transformation and upgrading [6].
The optimal scheduling of cogeneration can greatly promote energy conservation and emission reduction, improve environmental pollution status, and improve air quality. Cogeneration scheduling optimizes fuel use, lowers emissions, incorporates renewable energy sources, and guarantees legal compliance. This raises efficiency, sustainability, and environmental performance while reducing pollutants and improving air quality. With the rapid development of the economy, the “smog” phenomenon has become more and more common, causing noticeable damage to people’s health. Especially in northern China, many coal-fired units are used for power generation due to resource endowment and constraints. Every winter heating season, many small coal-fired heating boilers are put into operation, and other pollutants and dust particles into the atmosphere [7]. Large thermal power plants will have desulfurization, denitrification, and electrostatic precipitation equipment. A thermal power plant’s standard coal consumption must be continuously monitored to ensure sustainable operation. These factors include power generation efficiency, boiler and turbine efficiency, auxiliary power consumption, heat rate, plant design, operating conditions, and maintenance practices. Pollutant emissions will be significantly reduced Compared to other heating and power supply units [8].
Secondly, the optimized dispatching of cogeneration can also improve the heating quality, improve people’s livelihood, and develop the economy. The pollution of decentralized small coal-fired heating boilers is severe, and the equipment is relatively backward. Generally, the heating cannot be continued but can only be interrupted. The impact of environmental temperature and boiler pressure is relatively apparent, and the heating quality is low [9]. China’s industrial enterprises (smelting, steel, paper making, textile, etc.) are the primary users of heat consumption, and residential heating in northern winter is another primary market. With the continuous improvement of China’s urbanization rate, residential heating consumption is increasing. Improve the quality of heat supply, improve the living standard of residents, and stabilize industrial heat supply, with obvious benefits.
Finally, the optimal dispatching of cogeneration can save power generation costs and improve the comprehensive benefits of power generation enterprises. The combined heat and power generation technology not only produces electric energy but also produces heat energy. Connectivity of CHP systems to grid dispatching operations is achieved by market-based dispatch optimization, demand response, combined cycle operation, load following and peak shaving, energy storage integration, and renewable energy integration. It can improve the fuel utilization rate without increasing the fuel supply, save the fuel cost of power generation enterprises, and improve comprehensive efficiency. The thermal power plant is generally close to the load center, and the heating and power supply are digested nearby, reducing the cost of the transmission network and heat transmission pipeline and reducing the heating network’s network loss and heat loss. The combined heat and power generation mode can be better integrated into the whole grid dispatching operation, ease the tense power supply situation, and improve the power supply reliability and security of the power system [8].
To sum up, cogeneration has the advantages of saving energy, reducing pollution, and improving the reliability of heating. It will also enhance the quality of life of urban residents and play an immeasurable role in promoting economic development and reducing environmental pollution. Therefore, the research on the optimal scheduling strategy of cogeneration based on the DQN algorithm has vital practical significance.
2 Related works
Cogeneration uses the waste heat generated in the power generation process for heat supply in other places to maximize energy use [8]. The comparison between traditional heating and power supply modes and heat and power supply modes of cogeneration technology is shown in Figure 1. Several issues confront the Deep Q-Network (DQN) algorithm in cogeneration scheduling: complexity, computing demands, data requirements, model complexity, algorithm tuning, exploration vs exploitation, policy generalization, safety, and dependability.
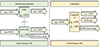 |
Figure 1 Schematic diagram of energy conversion of cogeneration optimization strategy. |
The energy conversion form in Figure 1 is analyzed, and it is proposed that the 80-kWh energy of traditional thermal power units can only produce 28 kWh of electrical energy [9]. The 100-kWh energy of the cogeneration unit can obtain 28 kWh of electric energy and 63 kWh of heat energy. The energy utilization rate is 35% and 90%, respectively. The energy utilization efficiency of cogeneration units is very high [10]. Therefore, if you want to achieve sustainable development, the development of cogeneration is an inevitable choice.
Much literature on stochastic optimization, robust optimization, or interval optimization for the optimization system of cogeneration [11]. In the stochastic optimization method, the multiple randomness in the CHP optimal scheduling system is described by probability function and solved by scenario method or parametric model transformation. Some literature uses multi-agent-based genetic algorithms to study the probabilistic economic scheduling problem of multi-energy power flow systems in the optimal scheduling system of cogeneration [12]. The scenario method is another method to describe multiple uncertain factors in the optimal scheduling system of cogeneration [13]. In addition, stochastic optimization based on chance constraints is also an uncertain optimization algorithm that is often used. This model mainly uses sampling average estimation, scene approximation, and other methods to transform the uncertain model for a solution [14, 15]. Although stochastic optimization uses probability distribution to describe uncertainty, it also has inevitable shortcomings. Due to the partial uncertainty of system parameters and data loss, obtaining a stable output for the system isn’t easy.
In addition, robust optimization is an uncertain optimization method that uses uncertain sets to represent the range of parameter changes. There are documents aimed at optimizing the economic cost of the day ahead electricity sales of the electricity heat and power cogeneration optimal scheduling system, using robust optimization to control the operation of heat and power cogeneration units, and improving the original linear control strategy into a segmented control strategy, to further ensure the effect of robust optimization and improve the conservatism of the algorithm [16–18].
In addition, the optimization of the combined heat and power generation optimal scheduling system has long been a concern by the academic community, and the research results in this area are relatively wealthy. Many literatures have studied the optimal management of integrated energy systems. However, the increasing complexity of the power system may lead to poor control performance obtained by conventional control methods. In some literature, traditional system modeling is used, and heuristic algorithms are used to adjust the controller’s parameters. Although these controllers perform relatively well, the heuristic algorithm will have lower exploration efficiency when the search space becomes more considerable. Some literature builds the optimization model of the cogeneration optimal dispatching system based on the constraints of the power network and the thermal network, based on which the overall benefits of wind power heating are discussed. Secondly, the optimal dispatching system of cogeneration is modeled by a set of stochastic differential equations, in which the nonlinear terms are obtained from the power prediction results through neural network technology, which is also an optimization means. The work suggests a deep reinforcement learning-based optimum dispatch strategy for integrated energy systems. Better response to dynamic changes is made possible by the method’s handling of the uncertainty surrounding user energy demand and renewable energy sources. The model is solved using the Asynchronous Advantage Actor-Critic method and has a well-constructed state space, action space, and reward function [19]. With an emphasis on the growing usage of intermittent renewable energy, the study investigates the application of Deep Reinforcement Learning (DRL) in gas turbine dispatch techniques.
A case study in Alberta, Canada, evaluates three prominent DRL algorithms; Deep Q-Networks (DQN) receives the most significant rewards. Additionally, the study suggests a way to dynamically allocate GT operating and maintenance expenses, leading to more practical regulations [20]. In conclusion, the research on the optimal scheduling strategy of cogeneration based on the DQN algorithm has a deep research foundation.
3 Optimal scheduling of cogeneration based on DQN
The modeling of the optimal dispatching system of cogeneration is the basis of the optimal analysis of the optimal dispatching system of cogeneration. The traditional modeling idea is to model various devices in the system separately, thus making up for the shortcomings of the conventional methods. The main idea includes the basic definition, simplified energy flow diagram, and energy balance equation generation process. In CHP generation optimum scheduling systems, the energy flow diagram visualizes energy flows, grid integration, and end-use loads to assist operators in understanding energy balances, optimizing system performance, and maximizing efficiency. It thoroughly understands the system’s functions, making well-informed decisions and optimization techniques easier. Taking the energy flow diagram of the combined heat and power generation optimal scheduling system as an example, this study briefly introduces the method’s application steps and modeling process.
Before modeling the system’s energy flow, the energy constraints of each subsystem in the cogeneration optimal scheduling system are discussed. Power flow is the “backbone flow” in the energy flow of the cogeneration optimal dispatching system. Power flow is essential for cogeneration optimum dispatching systems to balance supply and demand, optimize generation dispatch, manage grid restrictions, and maximize efficiency. It incorporates sustainable energy sources and adapts quickly to changes. For each node i, its active and reactive power calculation formulas (1) and (2) are as follows:![$$ {{\enspace P}}_{e,i}=\sum_{(i,j)\in {\mathrm{\Sigma }}_{\mathrm{ine}}}{E}_i{E}_j\left[{g}_{{ij}}\mathrm{cos}\left({\theta }_i-{\theta }_j\right)+{b}_{{ij}}\mathrm{sin}\left({\theta }_i-{\theta }_j\right)\right] $$](/articles/stet/full_html/2024/01/stet20240098/stet20240098-eq1.gif) (1)
(1)
![$$ {Q}_{e,i}=\sum_{(i,j)\in {S}_{\mathrm{ine}}}{E}_i{E}_j\left[{g}_{{ij}}\mathrm{sin}\left({\theta }_i-{\theta }_j\right)-{b}_{{ij}}\mathrm{cos}\left({\theta }_i-{\theta }_j\right)\right] $$](/articles/stet/full_html/2024/01/stet20240098/stet20240098-eq2.gif) (2)
(2)
Where i and j represent adjacent nodes, and power flows from node i to node j, g
ij
and b
ij
are respectively, and θ
ij
is the voltage phase angle of the two nodes of the line. The global relationship of power generation in the power grid should also meet the following inequality (3) constraints: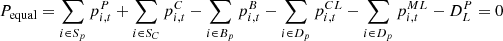 (3)
(3)
Among them,  refers to the power generation capacity of power supply equipment only,
refers to the power generation capacity of power supply equipment only, 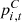 refers to the power generation capacity of cogeneration equipment,
refers to the power generation capacity of cogeneration equipment, 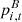 refers to the power consumption of electric boiler equipment,
refers to the power consumption of electric boiler equipment, 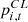 refers to the power consumption of controllable load,
refers to the power consumption of controllable load, 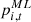 refers to the power consumption of necessary operating load, and
refers to the power consumption of necessary operating load, and 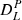 refers to the power consumption of transmission circuit. The power flow constraint on the transmission line should also satisfy the following inequality (4):
refers to the power consumption of transmission circuit. The power flow constraint on the transmission line should also satisfy the following inequality (4):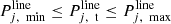 (4)
(4)
Wherein, 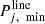 and
and 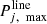 is the maximum and minimum values of power flow, respectively. In the gas flow model, natural gas comes from wells or storage devices and is delivered to users through special pipelines. The gas flow of natural gas is shown in equation (5).
is the maximum and minimum values of power flow, respectively. In the gas flow model, natural gas comes from wells or storage devices and is delivered to users through special pipelines. The gas flow of natural gas is shown in equation (5).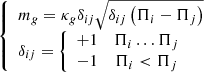 (5)
(5)
Wherein, m
g
is the natural gas flow in the pipeline; κ
g
is the characteristic constant related to the pipeline length, pipeline diameter, pipeline friction coefficient, temperature and pressure under standard conditions, the relative density of natural gas, air Changshu, 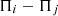 are the pressures of nodes i and j respectively, so the simplified equation (6) is:
are the pressures of nodes i and j respectively, so the simplified equation (6) is: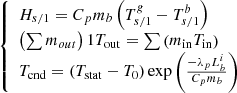 (6)
(6)
The global heat equivalent formula of the heating network is like that of the power network, as shown in equation (7) below: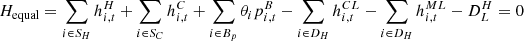 (7)
(7)
Among them, the power flow constraint of the thermal network shall meet the following relationship, as shown in equation (8):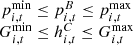 (8)
(8)
Wherein, its heat storage flow direction is shown in Figure 2.
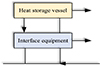 |
Figure 2 Flow direction of heat storage in cogeneration. |
The main difference is that when the generation capacity of distributed generators far exceeds the load demand, the energy storage system can store redundant energy, for example, for future use. To protect the energy storage system from being damaged by massive energy flow, the maximum charging/discharging amount is limited to a specific range. Infrastructure optimization, demand response, grid stability, renewable integration, cost savings, backup power, environmental advantages, and assistance for electric vehicles are all provided by energy storage systems. In addition to helping regulate peak energy usage, they encourage sustainability, lower greenhouse gas emissions, and enable fast-charging stations. Energy storage systems balance variables, including grid stability, battery longevity, and user requirements, while maintaining safe and effective operation through defined charging and discharging limitations. These restrictions can be changed to suit the user’s needs and vary depending on the technology, system size, and application. The energy storage system (SOC) of the energy storage system should be limited to an appropriate range of practical applications. Here, we express the control signal of the energy storage system in network i as uiBES. The charging/discharging power and SOC of the energy storage system in the sub-grid I are expressed as Pico energy storage system and SOC
i
. The constraint of p
i
and SOC
i
is equation (9):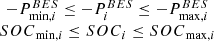 (9)
(9)
Wherein the battery charging and discharging system (BES) and SOC
i
of P at time t and t+1 are equation (10) and equation (11), respectively: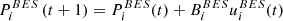 (10)
(10)
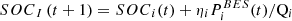 (11)
(11)
Then, based on the above mathematical model, the energy bus is defined as a unit with a complex and diverse multi-energy system modeled as a multi-input and output port. For example, the input port can be natural gas, electricity, heat energy, etc. Similarly, the output port can also be a variety of forms of energy. The coupling matrix C is the coupling relationship between input and output in a certain period. The CHP-based energy bus diagram can be selected from Figure 3 as a reference.
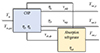 |
Figure 3 Structure of energy bus for cogeneration. |
Finally, the above formulas are simplified and integrated to model the energy flow, including the energy conversion equipment and its connection mode. The energy converter and its topology will be expressed as a matrix based on graph theory. Figure 4 shows the relationship between the above formula and the energy endpoint.
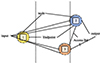 |
Figure 4 Energy conversion relation diagram of cogeneration. |
4 Methods
4.1 Model building and optimization
The relationship between the CHP system network and its regional subnet is connected through various gateways, and its transmission principle is like the information interaction in the big data Internet. In this paper, the optimal dispatching system of cogeneration is divided into three layers: dispatching layer, regional layer, and equipment layer, as shown in Figure 5:
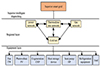 |
Figure 5 Schematic diagram of the optimized dispatching system for cogeneration. |
The dispatching center is an indispensable conduit for decision commands, protocol-based communication, real-time monitoring, and coordination. Energy management activities are made reliable and efficient using redundancy and security measures. The superior intelligent dispatching layer of the cogeneration optimization dispatching system has planned the location and capacity of the source equipment to provide initial conditions for the lower layer. Cogeneration optimization dispatching systems incorporate source equipment location and capacity based on several factors, including fuel availability, waste heat utilization, grid connection, energy demand, compliance with regulations, financial sustainability, resiliency, ecological impact, and future adaptability. The primary function is to coordinate the interaction between the lower-level and the upper-level power grid, provide security for the optimal dispatching system of cogeneration, and further save costs. At the regional level, the source equipment controllable distributed power sources within a specific range to achieve the effect of energy autonomous management. Controllable distributed power sources, improving resilience, sustainability, and economic prospects through energy supply diversification, increased flexibility, less environmental impact, and community empowerment should be the main objectives of future energy independence programs. The equipment layer is mainly composed of wind turbine, photovoltaic, energy storage, and other components, which are used to control the startup and shutdown of equipment and operation status, collect relevant parameters and execution instructions of equipment, and provide feedback the planned optimal value and energy distribution results to the upper layer, and constantly update the iterative configuration parameters to finally approach the optimal scheme. Its transmission architecture is shown in Figure 6.
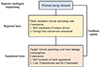 |
Figure 6 Structure of optimized dispatching and transmission of cogeneration. |
Currently, most power grid systems based on multi-agent systems have centralized control systems responsible for various activities. If they only communicate with adjacent nodes, these single nodes may not be able to make accurate decisions to adapt to the global situation, as shown in Figure 7.
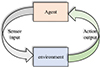 |
Figure 7 Interaction of intelligent sports environment system based on DQN algorithm. |
In Figure 7, the framework architecture shows a simplified grid system example. The total number of agents is the total number of generators, loads, and other types of equipment in the optimal dispatching system of cogeneration. Among them, the function of the dispatching center is to issue and transmit the decision commands of the superior dispatching agent to the regional layer and equipment layer and meet the power demand of various users. Precise forecasting, efficient management techniques, adaptable grid infrastructure, careful load prioritization, cutting-edge technology integration, and demand-side flexibility incentives are all necessary for balancing electricity demand. In the electricity supply, supportive regulatory frameworks encourage sustainability, dependability, and efficiency. Set the period t to divide the scheduling agent’s ability to adjust users into two types: adjustable load and non-adjustable load. The scheduling agent’s ability to regulate power usage distinguishes adjustable and non-adjustable loads.
In contrast to non-adjustable loads, which function independently, the agent may change adjustable loads. Fixed appliances and lighting fixtures are examples of non-adjustable loads, whereas HVAC systems and electric cars are changeable. The definition is shown in equation (12):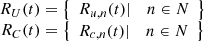 (12)
(12)
When the optimal dispatching system of cogeneration cannot meet users’ needs, the system can purchase electric energy from the external grid. Through interconnection agreements, renewable energy requirements, tariffs, and rate structures, guidelines and regulations oversee external grid procurement, guaranteeing grid dependability, fair competition, consumer protection, and environmental standards. When this happens, the adjustable load and non-adjustable load are equation (13):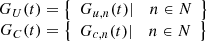 (13)
(13)
Several factors, including demand forecasts, fuel and electricity prices, heat demand profiles, grid constraints, environmental laws, CHP unit characteristics, system reliability, economic optimization, weather, operational limitations, and regulatory frameworks, impact cogeneration system dispatching decisions. Therefore, in period t, the dispatching decision of the dispatching center of the cogeneration power grid is the equation (14):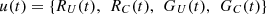 (14)
(14)
In addition, to meet the requirements of the interconnection of each region of the cogeneration optimal scheduling system, the hybrid framework of the cogeneration optimal scheduling system deploys a layered architecture, namely, the superior intelligent scheduling layer, the regional layer, and the equipment layer, to ensure rapid response to accurate information and accurate decision-making. Due to its model complexity, learning methodology, temporal difference learning, and experience replay, the Deep Q-Network (DQN) algorithm varies from Q-learning in real-time decision-making. While Q-learning is off-policy and model-free, DQN better manages high-dimensional state spaces. Enhancing decision-making for cogeneration optimum scheduling and complex systems requires the development of advanced analytics, machine learning, predictive modeling, renewable energy integration, innovative grid technologies, and policy frameworks. It should be noted that the superior dispatching layer can be further divided into the advanced dispatching intelligent layer, the intermediate dispatching intelligent layer, and the primary dispatching intelligent layer. The energy management system uses three dispatching intelligence levels—primary, intermediate, and advanced—. These levels are dedicated to real-time control, regional optimization, long-term planning, and strategic decision-making for grid operations that are dependable, efficient, and economical. Figure 8 shows the hierarchical architecture of the three superior intelligent scheduling level systems. The solid line indicates a two-way communication channel between two agents.
 |
Figure 8 Schematic diagram of intelligent hierarchical dispatching of CHP Based on DQN. |
In the layered scheduling model of the above-established cogeneration optimal scheduling system, the objective function, optimization decision variables, and constraints of the superior intelligent scheduling layer and the regional layer are inconsistent, and the regional total generation power is associated with them. Coordination and alignment are required because the advanced scheduling and regional layers of energy management systems differ in data granularity, time spans, decision-making complexity, information flow, and regulatory considerations. The superior intelligent scheduling and regional layers will exchange information to optimize the system’s scheduling effectively. The efficient flow of information between the intelligent scheduling layer and the regional layer optimizes several aspects of energy management operations, including system scheduling, constraint management, risk mitigation, flexibility, and performance monitoring, as shown in Figure 9 for the specific process.
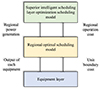 |
Figure 9 Interaction framework between the intelligent area layer and a dispatching layer of cogeneration. |
To save the total generation cost to the greatest extent, the superior intelligent dispatching layer optimizes the total output of several cogeneration optimal dispatching systems through smart algorithms. It transfers the total generation power of each region to the regional layer. The optimization of distributed equipment output, load balancing, demand response, resource sharing, and market integration are all made possible by generating power to regional layers, improving efficiency and resilience. Based on the total generation power received, each region optimizes the output of the distributed equipment, calculates the generation cost coefficient of different areas, and analyzes whether to transfer the coefficient to the superior intelligent dispatching layer for updating. The transmission range is relatively limited because the cold and hot energy transmission will cause severe losses. In this study, the optimization decision variable of the system level is the total regional power generation (not affected by the cold and heat variables), which links different energy systems together. In this way, the purpose of long-distance cross-region coupling of energy can be achieved, the loss can be effectively reduced, and the cost can be controlled in a lower range.
4.2 Data set extraction and preprocessing
The empirical test of the optimal dispatching model of cogeneration based on the DQN algorithm requires the first extraction of historical data of each unit. Determine the comprehensive standard coal consumption of the thermal power plant as the economic indicator and select the appropriate linear fitting tool to curve fit the historical data. The aims, assumptions, and features of the data all influence which linear fitting technique is optimal. Principal Component Regression (PCR), Elastic Net Regression, Robust Regression, Generalized Least Squares (GLS), Total Least Squares (TLS), Ridge, Lasso, and Ordinary Least Squares (OLS) are examples of typical alternatives. For curve fitting historical data, the best linear fitting tool will depend on several factors, including data properties, compatibility with assumptions, variable relationships, robustness to outliers, model complexity, handling high-dimensional data, quantification of uncertainty, performance, and the amount of computational resources needed for implementation. The historical data of four units are derived from SIS, and about 10000 data are extracted for each unit. The data includes five variables: power supply load, power generation load, instantaneous flow of coal feeder, low calorific value, and instantaneous heat of air extraction. According to the site requirements, the coal consumption data between 250 and 400 g/kWh and the power generation load data between 160 and 330 MW are screened out.
According to the analysis of power generation load and power supply coal consumption, the historical data provided on site are numerous and disordered, with abnormal data, data missing, and a series of problems. The fuel management, power generation, heat production, grid interaction, and environmental compliance subsystems are all integrated and comprise the Generalized Combined Heat and Power (CHP) Generation Optimal Scheduling System. Together, these subsystems balance heat and power production, control fuel usage, and meet system goals. There are various problems in the curve fitting of existing data directly. The data needs to be processed here. The singular point removal method is used here to remove unreasonable and abnormal data. A critical data processing step for linear fitting models is singular point removal to discover and remove outliers, enhance model accuracy, and maintain data integrity. Dependability needs validation and sensitivity analysis, which entail statistical techniques, subjectivity, and knowledge. For example, in the 195–200 MW load range of the unit, the coal consumption value corresponding to most of the data is 340–390 g/kWh, which is average data.
In comparison, the coal consumption data corresponding to very few data points is higher than 500 g/kWh or below 250 g/kWh. There are many reasons for this. It may be that the operating condition of the unit is unstable, or there may be a problem with the sensor for data monitoring. In short, this part of the data needs to be removed. In addition, in the analysis of power generation load and gross calorific value of coal, since the coal consumption for power supply is related to multiple variables on site and varies in real-time, the impact of other variables should be minimized when analyzing the relationship between power generation load and gross calorific value of coal. Understanding the linkages between power generation and how they affect energy efficiency, fuel choice, emissions, operational efficiency, financial concerns, and system stability depends on minimizing the gross calorific value (GCV). Although lower GCV fuels could be less expensive, they might produce less power and emit fewer pollutants. Therefore, the historical data of power generation load and gross calorific value of coal should be screened out when the extraction load is 0.
Then, in the unit model established, under the load rate constraint (30%~100%), the gas turbine generates a group of simulation data with a 5% load rate as the gradient, and each group of simulation data includes the sub-condition data with 5% heating power as the gradient. During the low-load operation of the gas turbine, the unit’s heating capacity is also limited and cannot reach 100% of the rated heating. The simulation database of the unit in line with the actual operation is obtained by removing this part of the data. According to the least squares method, there is equation (15):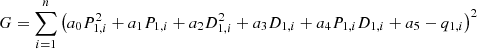 (15)
(15)
To minimize the sum of squares of residuals G, calculate the extreme value of the multivariate function to obtain equation (16):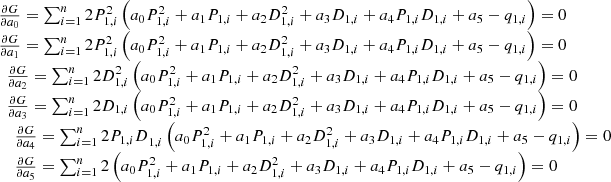 (16)
(16)
Then, solve the above data set to get equation (17)–(21):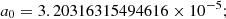 (17)
(17)
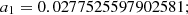 (18)
(18)
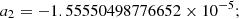 (19)
(19)
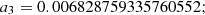 (20)
(20)
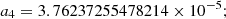 (21)
(21)
Then, we take the above four data sets as four different units for empirical verification and order analysis.
5 Case study
5.1 Fixed order analysis of optimization mathematical model for cogeneration scheduling
After the data processing in the previous step, the obtained data can be used for order determination analysis of the mathematical model. Because the last chapter has focused on the brief introduction of the fitting method, here only part of the field data is taken for experimental verification. The least squares approach is a well-liked option for curve fitting in experimental verifications because of its ability to comprehend statistical data, flexibility, robustness against outliers, and accuracy. It manages different curve forms, reduces discrepancies between actual and expected values, and analyses big datasets efficiently. Here, the least square method is selected to perform 1–9 order fitting for one unit, as shown in Figure 10:
 |
Figure 10 Fitting results of cogeneration equation lines with different times. |
As shown in the figure, appropriate orders should be selected to ensure the unit model’s accuracy. From the above figure, the second-order fitting effect obviously cannot fully reflect the unit’s coal consumption load characteristic curve. The fourth-order impact is more consistent with the actual operating conditions; the unit has an optimal load operation point, and the coal consumption will also be reduced when the unit operates at full load but not lower than the optimal load operation point. To guarantee a constant fourth-order effect under practical circumstances, pay close attention to accurate measurement, external control, experimental solid design, calibration, data quality assurance, adaptability, cross-validation, sensitivity analysis, and ongoing development. To build a simulation database that represents the natural functioning of a unit, historical data must be gathered, filtered for low load and restricted heating capacity times, segmented, and these data points removed. The remaining data must be validated, adjusted, and used for simulation testing to maximize performance parameters. To explore the selection of the number of orders and highlight the specific gap between orders, error analysis should be conducted on the fitting results of each order. The Curve Fitting Tool is selected here to calculate various indexes of different orders, and the results are shown in Table 1.
Comparison of indicators of different order results.
Through observation of the data in the table, it is found that the higher the fitting order, the better the effect. However, this is different in engineering practice. On the one hand, the higher the order, the more coefficients of the mathematical equation obtained by fitting, which is too complex in subsequent calculations using algorithms. On the other hand, it has high order and high fitting accuracy. In the actual production process, due to the unstable operating conditions of the unit, together with various interference factors such as inaccurate measurement data, the high-order fitting curve will have a solid response to the data with prominent anomalies because of the high accuracy. In short, the higher the order, the worse the robustness. Therefore, we choose the 6th order fitting through testing.
In Chapter 3, we get an optimal dispatching function for cogeneration, allocate four units respectively, and establish four load coal consumption characteristic curve equations. To minimize the overall coal consumption, we can combine the four equations into one function in the form of a weighted sum and bring them into the sequential quadratic programming method together with the established constraint equation to solve the optimal allocation scheme and minimum average coal consumption of four units can be obtained. Resource allocation on characteristic curves must be observed to evaluate efficiency, performance optimization, system dependability, cost containment, and environmental impact. It maximizes efficiency while ensuring maximum effectiveness, lowering expenses, and reducing emissions. Here, fmincon in MATLAB is used to input the total load of 987.2703 MW, and the following results are obtained after being brought into the program, as shown in Table 2:
Optimal allocation results of cogeneration based on sequential quadratic programming.
After distributing the total load, the average coal consumption is 301.3258 g/kWh. The drawing function is used here to express the characteristic curves of the four units, and the results obtained in Table 2 are calibrated in the distinctive curves of the units. The optimal allocation of the algorithm is verified by observing its position on the characteristic curves. The load characteristic curves of each unit are shown in Figure 11:
 |
Figure 11 Optimal operating load points corresponding to four units after load distribution. |
As shown in Figure 11, the horizontal axis 160–300 MW represents the load range. The vertical axis represents the coal consumption g/kwh. Each circle is the distribution optimization result after the total load is brought into the program. It can be seen from the figure that the small circle at the lowest point of the coal consumption characteristic curve is just the optimal operation point of each unit. It is the optimal operation point, showing that the optimal scheduling of the combined heat and power generation based on the DQN algorithm we proposed is feasible.
5.2 Model optimization results
This manuscript proposes an optimization strategy method based on the DQN algorithm for the scheduling system. The scenario of a generalized combined heat and power generation optimal scheduling system connected by multiple subsystems is considered. Each system is assumed to have many electrical equipment, including photovoltaic generators, users’ power demand, users’ heat demand, and external grid price. According to the energy optimization management principle of the optimal dispatching system of cogeneration, the minimum operating cost of the optimal dispatching system of cogeneration is defined as the objective function. When comparing operating costs in the cogeneration optimum scheduling system, the main goal is to evaluate how well the DQN and Q-learning algorithms optimize system performance while minimizing expenses. On this basis, a series of penalty functions are formulated. Table 3 shows the convergence of the model obtained by using the exact data for analysis and processing under three different methods.
Convergence of the model under three different optimization methods.
From the table, the calculation time of the model optimization solution in method 1 is 0.6 s, regardless of the initial value and step size of the penalty function; when methods 2 and 3 are adopted, with the increase of step size, no matter how significant the initial value is, the convergence result will have a specific deviation; When the step size is specified within a particular range, and the initial value is determined as 100, the result will be more accurate than the convergence result when the initial value is 1; Considering the particular case, the step size and initial value are both specified as 1, at this time, the model will not reach convergence. According to the above analysis, when the initial value is 100 and the step size is slightly greater than 1, the model has the fastest convergence speed and considers optimality. Therefore, the initial value of the model is 100, and the step size is 1.5.
Carry out simulation analysis according to the scheme defined above. The intelligent dispatching layer then uses the DQN algorithm to calculate the reward value and adjust the strategy parameters until the lowest operating cost is finally obtained. In this paper, 60 days of historical data is used as the training set, and 2 months of data are retained for training to ensure the integrity and consistency of the data. See Figure 12 for the number of iterations and prediction output.
 |
Figure 12 Prediction output of DQN Network. |
Figure 12 shows the iterative training process. This experiment iterates the intelligent experience through 2000 data to pursue the collaborative optimization of cogeneration.
In addition, to prove the effectiveness of the methods used in the cogeneration optimal scheduling system, DQN, and Q learning algorithms are used to compare the operating costs. The 60-day experimental data were compared. The optimal solution based on the Q learning algorithm gives 60 sample operations by averaging the optimal values, as shown in Figure 13.
 |
Figure 13 Variance comparison between DQN algorithm and other algorithms. |
It can be seen from the figure that the minimum operating cost can be achieved by comparing the two algorithms with and without intelligent optimization algorithms. Compared with the stochastic comparison optimization method based on DQN and Q learning, it can effectively reduce the operation cost of the optimal dispatching system of cogeneration. Because DQN uses the action value function to map the state to act, it will make real-time decisions according to the current situation, which performs better than the random optimization based on the Q-learning algorithm. A cogeneration optimum scheduling system with a high-dimensional, continuous state space employs various optimization techniques. There are benefits and drawbacks to using different techniques for tackling complicated optimization issues and exploring high-dimensional spaces, such as evolutionary strategies, gradient-based methods, simulated annealing, particle swarm optimization, and genetic algorithms. However, due to the CHP optimal scheduling system’s high-dimensional and continuous state space, it is more difficult to obtain the most rewarding behavior through learning the value based on DQN. Therefore, DQN will oscillate and train near the optimal value function in the optimal state but will not converge. As shown in Table 4 and Table 5, the results of optimization using the DQN algorithm are closest to the target curve, and the results of optimization using the Q learning algorithm and optimization without the algorithm deviate from the target curve.
Comparison results of different methods (costs).
Comparison results of different methods (time consumption).
Obviously, for the scheduling optimization system of cogeneration, the simulation of DQN strategy based on a neural network takes less time to converge than Q learning, which shows the ability of real-time in practical application. Therefore, DQN will oscillate and train near the optimal value function in the optimal state but will not converge.
6 Conclusion
According to the DQN algorithm, this manuscript has built a practical optimal dispatching model for cogeneration. The initial value of the model is 100, the step size is 1.5, and a 6-order function is selected for fitting. A representative load model is studied to build energy systems involving different forms. Based on taking into account the load, the optimal dispatching of the integrated energy system is completed, and the processing situation and total cost of each system after optimization are calculated, making more effective use of energy and controlling the total cost in a lower range. Based on the analysis of the calculation results, the model created in this paper can be decoupled by using thermal power determination. Based on the total cost objective function, the optimization of the three electric heating and cooling loads is completed. The expected joint dispatching goal is achieved, and the model performance is improved by 8.96%. It significantly reduces energy costs, optimizes resource allocation, and enhances the system’s adaptability.
Funding
The authors did not receive any funding.
Conflicts of interest
Authors do not have any conflicts.
Data availability statement
No datasets were generated or analyzed during the current study.
Author contribution statement
Pei Zhang and Yan Fu are responsible for designing the framework, analyzing performance, validating the results, and writing the article. Fu Yao is responsible for collecting the information required for the framework, providing software, conducting critical reviews, and administering the process.
References
- Roy P.K., Ghosh M. (2017) Combined heat and power dispatch using hybrid genetic algorithm and biogeography-based optimization, Int. J. Energy Optimiz. Eng. (IJEOE) 6, 1, 49–65. [Google Scholar]
- Shuai H., He H. (2020) Online scheduling of a residential microgrid via Monte-Carlo tree search and a learned model, IEEE Trans. Smart Grid 12, 2, 1073–1087. [Google Scholar]
- Dan M., Srinivasan S., Sundaram S., Easwaran A., Glielmo L. (2020) A scenario-based branch-and-bound approach for MES scheduling in urban buildings, IEEE Trans. Industr. Inform. 16, 12, 7510–7520. [CrossRef] [Google Scholar]
- Chen M., Shen Z., Wang L., Zhang G. (2022) Intelligent energy scheduling in renewable integrated microgrid with bidirectional electricity-to-hydrogen conversion, IEEE Trans. Netw. Sci. Eng. 9, 4, 2212–2223. [CrossRef] [Google Scholar]
- Suchetha C., Ramprabhakar J. (2018) Optimization techniques for operation and control of microgrids a review, J. Green Eng. 8, 4, 621–644. [CrossRef] [Google Scholar]
- Sun Q., Fan R., Li Y., Huang B., Ma D. (2019) A distributed double-consensus algorithm for residential we-energy, IEEE Trans. Industr. Inform. 15, 8, 4830–4842. [Google Scholar]
- Pei W., Ma X., Deng W., Chen X., Sun H., Li D. (2019) Industrial multi-energy and production management scheme in cyber-physical environments: a case study in a battery manufacturing plant, IET Cyber-Phys. Syst. Theor. Appl. 4, 1, 13–21. [CrossRef] [Google Scholar]
- Zhou X., Zou S., Wang P., Ma Z. (2020) Optimal energy management in combined heat and power system via a decentralized consensus-based ADMM, IFAC-Papers OnLine 53, 2, 4026–4031. [CrossRef] [Google Scholar]
- Yang L., Xie P., Zhang R., Cheng Y., Cai B., Wang R. (2019) HIES: cases for hydrogen energy and I-energy, Int. J. Hyd. Energy 44, 56, 29785–29804. [CrossRef] [Google Scholar]
- Wang Y., Wang Y., Huang Y., Yu H., Du R., Zhang F., Zhu J. (2018) Optimal scheduling of the regional integrated energy system considering economy and environment, IEEE Trans. Sustain. Energy 10, 4, 1939–1949. [Google Scholar]
- Ren M., Jiang X., Yuan J. (2020) Wind power integration and emission reduction via coal power retrofits in China’s quota-based dispatch system: a case study of Jilin Province, Environ. Sci. Pollut. Res. 27, 10, 11364–11374. [CrossRef] [PubMed] [Google Scholar]
- Wang D., Wang C., Lei Y., Zhang Z., Zhang N. (2019) Prospects for key technologies of new-type urban integrated energy system, Glob. Energy Interconnect. 2, 5, 402–412. [CrossRef] [Google Scholar]
- Zhang C., Su Q., Zhu Y. (2023) Urban park system on public health: underlying driving mechanism and planning thinking, Front. Public Health 11, 1193604. [CrossRef] [Google Scholar]
- Zhou J., Li B., Zhang D., Yuan J., Zhang W., Cai Z. (2023) UGIF-Net: an efficient fully guided information flow network for underwater image enhancement, IEEE Trans. Geosci. Remote Sens. 61, 1–17, Art no. 4206117, doi: 10.1109/TGRS.2023.3293912. [Google Scholar]
- Ali J., Shan G., Gul N., Roh B.H. (2023) An intelligent blockchain-based secure link failure recovery framework for software-defined internet-of-things, J. Grid Comput. 21, 4, 57. [CrossRef] [Google Scholar]
- Ali J., Jhaveri R.H., Alswailim M., Roh B.-H. (2023) ESCALB: an effective slave controller allocation-based load balancing scheme for multi-domain SDN-enabled-IoT networks, J. King Saud Univ.-Comput. Inform. Sci. 35, 6, 101566. [Google Scholar]
- Dong Q., Liu X. (2023) Optimization practice of university innovation and entrepreneurship education based on the perspective of OBE, J. Combinat. Math. Combinat. Comput. 118, 181–189. [CrossRef] [Google Scholar]
- Liao Q. (2023) English teaching project quality evaluation based on deep decision-making and rule association analysis, J. Combinat. Math. Combinat. Comput. 118, 119–127. [CrossRef] [Google Scholar]
- Zhou X., Wang J., Wang X., Chen S. (2023) Optimal dispatch of integrated energy system based on deep reinforcement learning, Energy Rep. 9, 373–378. [CrossRef] [Google Scholar]
- Sage M., Staniszewski M., Zhao Y.F. (2023) Optimal economic gas turbine dispatch with deep reinforcement learning, IFAC-Papers OnLine 56, 2, 10039–10044. [CrossRef] [Google Scholar]
All Tables
Optimal allocation results of cogeneration based on sequential quadratic programming.
All Figures
 |
Figure 1 Schematic diagram of energy conversion of cogeneration optimization strategy. |
| In the text | |
 |
Figure 2 Flow direction of heat storage in cogeneration. |
| In the text | |
 |
Figure 3 Structure of energy bus for cogeneration. |
| In the text | |
 |
Figure 4 Energy conversion relation diagram of cogeneration. |
| In the text | |
 |
Figure 5 Schematic diagram of the optimized dispatching system for cogeneration. |
| In the text | |
 |
Figure 6 Structure of optimized dispatching and transmission of cogeneration. |
| In the text | |
 |
Figure 7 Interaction of intelligent sports environment system based on DQN algorithm. |
| In the text | |
 |
Figure 8 Schematic diagram of intelligent hierarchical dispatching of CHP Based on DQN. |
| In the text | |
 |
Figure 9 Interaction framework between the intelligent area layer and a dispatching layer of cogeneration. |
| In the text | |
 |
Figure 10 Fitting results of cogeneration equation lines with different times. |
| In the text | |
 |
Figure 11 Optimal operating load points corresponding to four units after load distribution. |
| In the text | |
 |
Figure 12 Prediction output of DQN Network. |
| In the text | |
 |
Figure 13 Variance comparison between DQN algorithm and other algorithms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




