| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
Decarbonizing Energy Systems: Smart Grid and Renewable Technologies
|
|
|---|---|---|
| Article Number | 45 | |
| Number of page(s) | 22 | |
| DOI | https://doi.org/10.2516/stet/2024034 | |
| Published online | 05 August 2024 | |
Regular Article
Enhanced Randomized Harris Hawk Optimization of PI controller for power flow control in the microgrid with the PV-wind-battery system
School of Electrical and Electronics, Department of Electrical and Electronics Engineering, Sathyabama Institute of Science and Technology, Chennai 600119, India
* Corresponding author: pavanphd80@gmail.com
Received:
18
January
2024
Accepted:
15
May
2024
Microgrids, characterized by their ability to work individually or in combination with the main power system, play a pivotal role in addressing the growing demand for reliable and sustainable energy solutions. This work concentrates on the integration of sustainable energy sources, specifically photovoltaic (PV), and wind generation and a battery storage system within a microgrid framework. Additionally, a power flow control strategy is implemented to enhance the dynamic behaviour and stability of the microgrid. The proportional-integral (PI) controller is a fundamental component in regulating the microgrid’s power flow, ensuring optimal performance under varying operating conditions. However, tuning the PI controller parameters is a difficult task because of the dynamic and nonlinear nature of renewable energy sources. In this work, the application of the Enhanced Randomized Harris Hawk Optimization (ERHHO) to fine-tune the PI controller is proposed, using the algorithm’s ability to mimic the hunting behaviour of hawks in finding optimal solutions. The PV-Wind-Battery microgrid system is modelled, and the proposed algorithm is employed to optimize the PI controller parameters for efficient energy management. The ERHHO algorithm’s exploration-exploitation balance is harnessed to navigate the complex solution space and converge to optimal PI controller settings, thereby enhancing the microgrid’s stability and performance. The study evaluates the effectiveness of the proposed ERHHO-based PI controller tuning through comprehensive simulations. Performance metrics such as transient response, overshoot, settling time, and steady-state error are analysed to validate the robustness and efficiency of the proposed method. Compared to its nearest optimization algorithm, with the proposed algorithm rise time is reduced by 50%, overshoot is reduced by 75%, settling time is reduced by 66%, and finally, a percentage of reduction of steady-state error is 45%. The outcomes of this research contribute to the advancement of microgrid control strategies, offering a novel approach to PI controller tuning in the context of diverse renewable energy sources. The integration of the Harris Hawk Optimization algorithm provides a promising avenue for enhancing the operational efficiency and reliability of microgrids, paving the way for sustainable and resilient energy systems in the aspect of growing energy landscapes.
Key words: Microgrid / Renewable energy / Photovoltaic (PV) / Wind generation / Proportional-integral (PI) controller / Harris Hawk Optimization (HHO) algorithm / Microgrid stability / Simulation analysis
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Distributed Generations (DGs) emerge as a viable remedy for the prevalent challenges encountered by global energy systems. The challenges are related to network overloading, greenhouse gas emissions, system stability and reliability and elevated utilization costs. The application of power flow control in microgrids for substantial commercial structures introduces complexities in curtailing network load deviations and running expenses [1]. The integration of a power flow control within a Microgrid (MG) holds the promise of diminishing working costs and enhancing energy utilization efficiency [2]. DGs encompass a diverse array of energy sources, spanning renewable options like wind turbines (WT), and photovoltaic (PV) systems, and alongside non-renewable alternatives such as micro-turbines (MT), diesel generators (DiG), and gas engines (GE) [3]. Microgrids consist of various integral components, including flexible load management, DGs, and storage devices [4]. Equipped with controllers, this microgrid model adeptly manages the system by regulating loads to optimize solar output. Furthermore, it facilitates bidirectional power flow, enabling the utilization of power from residential homes, hostels, and academic departments [5, 6].
Power flow control in microgrids can operate in either centralized or decentralized modes [7]. In centralized modes, the microgrid’s power exchange primarily depends on market prices, whereas decentralized modes allow for autonomous power exchange without being constrained by market prices [8, 9]. Microgrids confront significant challenges related to stability, efficiency, and energy protection. These challenges arise from factors such as reverse power flow from power sources voltage instability, transient states within the microgrid, notable frequency changes in standalone operating modes, and uncertainties in availability management dynamics. Ensuring appropriate load allocation, specifically during system vulnerability, often requires microgrids to employ high levels of angle droop. Power flow control also suffers from various challenges like increasing penetration of renewable energy sources, dynamic load variations and voltage and frequency regulation. To tackle these issues, a comprehensive tuning of controller gains is required to improve the performance of microgrids [10, 11].
In recent times, researchers have introduced resilient and innovative strategies inspired by nature to effectively tackle complex challenges like Proportional Integral controller (PI) tuning across diverse domains. Famous methodologies include Genetic Algorithm (GA) [12], Particle Swarm Optimization (PSO) [13], and various others [14]. In [15], a novel technique called Chaos Cultural Sine–Cosine Algorithm (CCSCA) was introduced to address premature convergence issues in the Sine–Cosine Algorithm (SCA). This approach incorporates a social algorithm as the population structure and utilizes disordered methods for particle search. Performance evaluation on benchmarking functions demonstrated that the CCSCA surpassed the basic SCA algorithm in global search capability, producing superior results. In [16], a binary Sine–Cosine Algorithm (SCA) approach was suggested to direct the unit commitment problem. The binary SCA approach utilized enhanced sigmoidal features to effectively represent the continuous search space. Results showcased the efficiency of the binary SCA method related to alternative approaches. In [17], introduced a discrete version of the Sine–Cosine Algorithm (SCA) designed for optimizing complicated problems. The effectiveness of the proposed discrete SCA was demonstrated through multiple benchmark functions, emphasizing its efficiency.
In [18], a hybrid optimization depending on the Sine–Cosine Algorithm (SCA) was developed to effectively tackle optimization problems. This hybrid approach integrates concepts and operators from various algorithms, fostering a robust interchange of exploration and exploitation capabilities. To evaluate its effectiveness, seven benchmark functions were employed. The outcomes revealed that the proposed hybrid method surpassed other similar approaches, providing a highly competitive solution. In [19], a novel hybrid algorithm named Steady State Genetic Algorithm (SSGA) was introduced for tackling complex problems. This hybrid method amalgamates the exploration advantages of the SCA with the capability of a steady-state genetic algorithm to avoid premature convergence. The results illustrate that the SSGA method significantly enhances the operation of complex design problems in comparison to similar optimisation methods.
In [20], a novel approach was introduced that integrates the Sine–Cosine Algorithm (SCA) for learning and initializing individuals to solve diverse optimization problems. This method is enhanced by incorporating nearly contradictory learning approaches and methods incorporating contrasting principles, thereby improving the effectiveness and speed of overall exploration. The efficacy of the proposed method was assessed by standard functions, and the results underscored its superiority over alternative approaches, showcasing significant performance improvements.
In [21], an innovative approach was employed by combining the gravitational search method with the firefly optimizing technique. This combined methodology aimed to improve the adjustment of controller settings and was applied within a 2 area hydrothermal power system. In [22], researchers adopted the arithmetic optimization approach (AOA) to meticulously fine-tune a fuzzy-PID controller. This fine-tuning process is adopted in the impact of the high voltage direct current (HVDC) link, strategically addressing the limitations associated with alternating current (AC) transmission.
In [23], researchers implemented a flower pollination optimization algorithm (FPOA) within Multi-Agent Power Systems (MAPSs) to develop a Proportional-Integral-Derivative (PID) controller utilizing spontaneous flower pollination techniques. To address Load Frequency Control (LFC) in interconnected MAPSs, a bacterial foraging approach was incorporated, subject to Particle Swarm Optimization (PSO), with a focus on the Proportional-Integral (PI) controller. This was applied under various fitness functions, encompassing both standard and customized criteria, and considered two segments within non-reheat thermal systems [24].
In [25], an advanced technique called the Hybrid Sine–Cosine Algorithm (HSCA) was formulated, using SCA to address optimization problems. The results demonstrated that the proposed HSCA consistently outperforms other relevant approaches, yielding superior scheduling outcomes across multiple cases. Its capacity to produce higher-quality results establishes its effectiveness in addressing optimization challenges.
The increasing integration of renewable energy sources, within microgrids has spurred the need for effective control strategies to optimize energy management. Proportional-Integral (PI) controllers play a crucial role in regulating system dynamics and ensuring stability. Microgrids serve diverse loads with varying power consumption patterns. The dynamic nature of these load profiles introduces challenges in PI controller tuning, as controllers must be able to adapt to changes in load demand quickly and efficiently to maintain grid stability and ensure reliable power supply. Microgrids are designed to operate both connected to the main grid and in islanded mode, where they function independently during grid outages. PI controllers must be tuned to facilitate a smooth transition between grid-connected and islanded modes while maintaining voltage and frequency stability within acceptable limits. The dynamics of microgrid components, such as inverters and energy storage systems, can exhibit nonlinear behaviour under certain operating conditions. Tuning PI controllers to effectively regulate these nonlinear dynamics while ensuring stability and performance is a complex task that requires careful consideration of system dynamics and control strategies.
The focus of this study revolves around utilizing the Enhanced Randomized Harris Hawk Optimization (HHO) algorithm for tuning PI controllers within the power flow control of a microgrid featuring PV, and wind generation. The complex relationship of these diverse energy sources necessitates an intelligent optimization approach to fine-tune the PI controllers, thereby enhancing the overall performance and efficiency of the microgrid. This research explores the application of ERHHO in the PI controller tuning, aiming to attain an optimal balance among energy generation, utilization, and system stability in a microgrid incorporating a mix of renewable and conventional energy sources.
2 Hybrid DG system (HDGS)
The schematic of the hybrid system is presented in Figure 1. The PV-wind-battery system contains a wind turbine, PV system and battery, working in hybrid to facilitate energy transfer from the DC bus to the grid. The PV generation system is connected to the DC bus through an MPPT-operated DC-DC converter. The wind generation system is connected to the DC bus through a rectifier and MPPT-operated DC-DC converter. The battery storage system is connected to the DC bus through a bidirectional DC-DC converter. The design of power flow control and management modules for the PV-wind-battery system unit is derived from the operational modes of the load and grid. During the grid-connected mode, the active and reactive output powers of the PV-wind-battery system unit are adjusted to align with their corresponding reference values. Therefore, the voltage source inverter (VSI)-based control system must select the suitable power control mode to ensure optimal performance. A sinusoidal pulse width modulation (SPWM) is adopted to control the VSC. To accommodate varying load requirements, the power provided by the main grid and PV-wind-battery system needs to be flexibly adjusted. Maintaining a consistent supply of active and reactive power necessitates the efficient control of power flow among the PV-wind-battery system and the grid and load. Additionally, a reliable connection between the power obtained from the main grid and the DG system is essential for meeting the load demand [26].
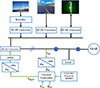 |
Figure 1 Management structure of HDGS with the proposed controller. |
The power balance equation must be fulfilled by the DC-link and point of common coupling (PCC). Total DC Power available at DC bus by energy sources in a microgrid is defined as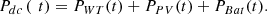 (1)
(1)
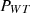 power generated by wind generation system,
power generated by wind generation system, 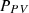 power generated by solar generation system,
power generated by solar generation system, 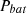 battery power measured at the output of the respective DC/DC converters.
battery power measured at the output of the respective DC/DC converters. 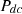 available DC power at DC bus.
available DC power at DC bus.
The total power generated by renewable sources is determined using equation (1), which incorporates the total power flow model. The power balance is computed by considering the output of the hybrid sources and the load demand at the AC bus.![$$ \begin{array}{c}{P}_g(t)=\left[{P}_l(t)-{P}_{{hres}}(t)\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq6.gif) (2)
(2)
![$$ \begin{array}{c}{P}_l(t)=\left[{P}_{{hres}}(t)+{P}_g(t)\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq7.gif) (3)
(3)
![$$ \begin{array}{c}{Q}_g(t)=\left[{Q}_l(t)-{Q}_{{hres}}(t)\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq8.gif) (4)
(4)
![$$ \begin{array}{c}{Q}_l(t)=\left[{Q}_{{hres}}(t)+{Q}_g(t)\right].\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq9.gif) (5)
(5)
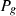 is active power provided by the grid,
is active power provided by the grid,  reactive power by the grid,
reactive power by the grid, 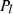 load active power,
load active power, 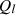 load reactive power,
load reactive power, 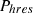 active power generated by HDGS and
active power generated by HDGS and 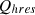 reactive power by HDGS.
reactive power by HDGS.
The battery power of the storage unit is influenced by the duration of discharge, where it acts as an energy source, and the duration of charging, where it functions as a load. However, ensuring a consistent power balance proves challenging due to the nonlinear fluctuations on the consumer side and the unpredictable nature of sustainable energy [27]. To tackle this challenge, the system unit requires a high-performance operation mode that enables efficient power regulation. The active and reactive power calculated by direct and quadrature axis voltages and currents are given as shown in equations (6) and (7).![$$ \begin{array}{c}{P}_I(t)=\frac{3}{2}\left[{v}_d*{i}_d+{v}_q*{i}_q\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq16.gif) (6)
(6)
![$$ \begin{array}{c}{Q}_I(t)=\frac{3}{2}\left[{v}_q*{i}_d+{v}_d*{i}_q\right].\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq17.gif) (7)
(7)
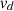 and
and  are direct and quadrature axis load voltages,
are direct and quadrature axis load voltages, 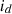 and
and 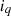 are direct and quadrature axis load currents.
are direct and quadrature axis load currents.
3 Modelling of sources
3.1 Mathematical formulation of solar PV module
The simplified circuit representation of a solar panel is depicted in Figure 2.
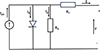 |
Figure 2 Equivalent circuit of real model for PV panel. |
The PV cell can be defined as an ideal current source denoted as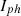 with a series of parallel resistances as shown in Figure 2. The output current of an ideal solar cell is described in equation (8)
with a series of parallel resistances as shown in Figure 2. The output current of an ideal solar cell is described in equation (8)
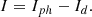 (8)
(8)
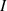 is PV output current,
is PV output current, 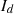 is diode current,
is diode current, 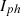 photon current.
photon current.
In the realm of semiconductor theory, the primary mathematical equation that interprets the I-V characteristics of the PV cell is known as Shockley’s diode current equation, as depicted in equation (9).![$$ \begin{array}{c}{{I}}_{{d}}={{I}}_{{s}}\enspace \left[\mathbf{exp}\enspace \left(\frac{{q}{{V}}_{{oc}}}{{{N}}_{{s}}\enspace {KA}{{T}}_{{o}}}\right)-\mathbf{1}\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq27.gif) (9)
(9)
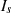 is the saturation current,
is the saturation current, 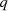 is the electron charge,
is the electron charge, 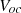 is the open circuit voltage,
is the open circuit voltage, 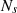 series connected cells per module,
series connected cells per module,  Boltzmann’s constant,
Boltzmann’s constant, 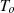 nominal cell temperature in kelvin.
nominal cell temperature in kelvin.
Given the sensitivity of the photovoltaic (PV) generation output to weather conditions such as irradiance and temperature, the use of a DC-DC converter becomes crucial for regulating both the output voltage and power. Figure 3 illustrates the importance of regulating the PV voltage to maximum power point voltage (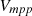 ), a critical factor in harnessing the peak power potential from the PV arrays by the implementation of a DC-DC converter. The maximum power point voltage of a PV panel can be determined from its characteristic curve, often referred to as the IV curve (current-voltage curve) or P-V curve (power-voltage curve). The P-V curve shows the relationship between the power output (P) and the voltage (V) across the terminals of the PV panel. It is derived from the IV curve and provides insights into the maximum power point (MPP) at which the panel operates most efficiently. The peak point on the P-V curve where the power output (P) is maximized represents the maximum power point (MPP) of the PV panel. As depicted in Figure 3, the control of PV voltage to reach
), a critical factor in harnessing the peak power potential from the PV arrays by the implementation of a DC-DC converter. The maximum power point voltage of a PV panel can be determined from its characteristic curve, often referred to as the IV curve (current-voltage curve) or P-V curve (power-voltage curve). The P-V curve shows the relationship between the power output (P) and the voltage (V) across the terminals of the PV panel. It is derived from the IV curve and provides insights into the maximum power point (MPP) at which the panel operates most efficiently. The peak point on the P-V curve where the power output (P) is maximized represents the maximum power point (MPP) of the PV panel. As depicted in Figure 3, the control of PV voltage to reach 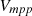 is essential for maximizing power extraction from the PV arrays via the DC-DC converter. The P&O MPPT (Perturb and Observe Maximum Power Point Tracking) algorithm, shown in Figure 4, is employed to generate the duty cycle necessary for the DC-DC converter to achieve maximum power extraction. Figure 5 presents the DC-DC converter utilized for the PV array.
is essential for maximizing power extraction from the PV arrays via the DC-DC converter. The P&O MPPT (Perturb and Observe Maximum Power Point Tracking) algorithm, shown in Figure 4, is employed to generate the duty cycle necessary for the DC-DC converter to achieve maximum power extraction. Figure 5 presents the DC-DC converter utilized for the PV array.
 |
Figure 3 I-V and P-V characteristics of PV array. |
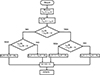 |
Figure 4 MPPT algorithm. |
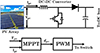 |
Figure 5 PV system with boost converter. |
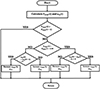 |
Figure 6 MPPT flow chart for wind generation. |
The Perturb and Observe (P&O) algorithm is a widely used MPPT technique in PV systems. It is a simple and efficient method for continuously adjusting the operating point of a PV system to ensure it operates at its maximum power point (MPP), where the power output is maximized. The algorithm starts by initializing the operating point of the PV system. This can be done by setting the operating voltage or current to a predetermined value, typically close to the expected MPP. The algorithm measures the power output of the PV system at the current operating point. This can be done by multiplying the current and voltage readings obtained from the PV system. Based on the power measurement obtained in the previous step, the algorithm perturbs the operating point by either increasing or decreasing the voltage or current slightly. This perturbation is typically small to ensure that the system remains near the MPP. After perturbing the operating point, the algorithm measures the power output of the PV system at the new operating point. The algorithm compares the power output at the new operating point with the power output at the previous operating point. If the power output has increased, it continues to perturb the operating point in the same direction. If the power output has decreased, it reverses the direction of perturbation. These steps are repeated iteratively, continuously adjusting the operating point of the PV system based on the comparison of power outputs at different points.
By continuously adjusting the operating point based on the observed changes in power output, the P&O algorithm converges towards the MPP of the PV system. However, it’s worth noting that the P&O algorithm may oscillate around the MPP, especially under rapidly changing environmental conditions or when the system is operating near local power maxima that are not the global MPP. To mitigate these issues, advanced MPPT algorithms with additional features and control strategies may be used in conjunction with or instead of the P&O algorithm. Nonetheless, the P&O algorithm remains popular due to its simplicity and effectiveness in many PV system applications.
3.2 PMSG and wind turbine
Output power from a wind turbine (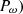 is given as in equation (11)
is given as in equation (11)
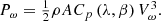 (11)
(11)
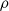 is the air density,
is the air density, 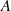 wind turbine swept area in m2,
wind turbine swept area in m2, 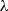 is the tip speed ratio,
is the tip speed ratio, 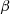 is the pitch angle. The tip speed ratio “
is the pitch angle. The tip speed ratio “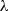 ” is defined as the ratio between the blade tip speed “
” is defined as the ratio between the blade tip speed “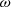 ,” the wind turbine blade radius “r,” and the wind speed “
,” the wind turbine blade radius “r,” and the wind speed “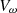 ,” and it can be expressed by equation (2).
,” and it can be expressed by equation (2).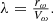 (12)
(12)
Hence, the mechanical energy generated by wind turbines may be regulated by adjusting both “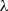 ” and “
” and “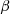 .” For any given “
.” For any given “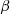 ,” there exists a respective power coefficient (
,” there exists a respective power coefficient (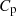 ) vs tip speed ratio (
) vs tip speed ratio (
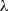 ) plot, where each curve has an optimal
) plot, where each curve has an optimal 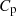 value, denoted as
value, denoted as 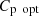 corresponding to an optimal tip speed ratio,
corresponding to an optimal tip speed ratio, 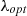 . By controlling these parameters, the mechanical energy of the turbine can be adjusted to match the available wind speed, with the maximum
. By controlling these parameters, the mechanical energy of the turbine can be adjusted to match the available wind speed, with the maximum 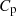 attained at the optimized rotational speed when “
attained at the optimized rotational speed when “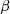 ” equals zero.
” equals zero.
The mechanical energy generated by wind turbines is converted into electrical energy with a PMSG (Permanent Magnet Synchronous Generator). The voltage and current relation for the PMSG are defined as shown in equations (13) and (14):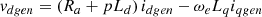 (13)
(13)
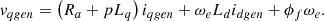 (14)
(14)
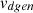 and
and 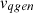 correspond to the stator dq-axis voltages of the PMSG, while
correspond to the stator dq-axis voltages of the PMSG, while 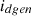 and
and 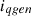 represent the stator dq-axis currents of the PMSG.
represent the stator dq-axis currents of the PMSG.
The electromechanical developed torque Te is determined as provided in equation (15):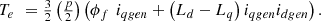 (15)
(15)
In the equation, 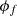 represents the amplitude of the flux linkage, and p denotes the pole pairs.
represents the amplitude of the flux linkage, and p denotes the pole pairs. 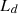 direct axis inductance,
direct axis inductance, 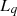 quadrature axis inductance,
quadrature axis inductance,
The relationship between mechanical torque and speed is defined by equation (16)
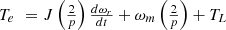 (16)
(16)
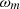 rotor speed in rad/s,
rotor speed in rad/s, 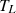 is load torque in N/m.
is load torque in N/m.
The power produced by the PMSG can be regulated by a DC-DC converter. This converter is operated by an MPPT algorithm. Before the DC-DC boost converter takes control of the regulation, the PMSG’s output is connected to a diode bridge rectifier.
To improve the dynamic performance of the wind generation system, an adjustable step size (P and O) algorithm is used to guide and manage the DC-DC converter. This approach ensures that the system reaches its peak power output. Differing from traditional P&O algorithms, this adaptive method tackles numerous shortcomings that can adversely affect the performance of the wind generation system, especially in systems characterized by inertia. Traditional P&O algorithms encounter a substantial challenge when it comes to selecting the optimal step size for rotor speed adjustments.
The P&O algorithm for MPPT in wind generation systems involves continuously perturbing the turbine parameters (such as rotor speed or blade pitch angle) and observing the resulting changes in power output. It begins by detecting variations in wind speed, typically measured using an anemometer. Once a change in wind speed is detected, the algorithm perturbs the turbine parameters in a specific direction (e.g., increasing rotor speed) and observes the resulting change in power output. If the power output increases, the algorithm continues perturbing in the same direction. However, if the power output decreases, it reverses the perturbation direction. This continuous adjustment process helps the algorithm converge towards the Maximum Power Point where the wind turbine operates most efficiently. The P&O algorithm iteratively adjusts turbine parameters based on the observed changes in power output, aiming to reach the MPP. It repeats this process until the algorithm converges to a stable operating point where further parameter adjustments do not significantly increase power output. The algorithm continuously monitors wind conditions and adjusts turbine parameters accordingly to maintain optimal performance, ensuring efficient power extraction from the wind.
The step size during the perturbation process can either stay the same or vary. Using a constant step size in Conventional P&O algorithms can present certain difficulties. To address these limitations, an adjustable step P&O algorithm is used, with the step size determined by the wind speed. By making use of the wind turbine characteristics, estimate the parameter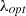 , which is typically around 8.1. Afterwards, calculate the optimal rotor speed using equation (17), as shown below:
, which is typically around 8.1. Afterwards, calculate the optimal rotor speed using equation (17), as shown below: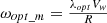 (17)
(17)
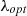 optimal tip speed ratio,
optimal tip speed ratio,
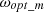 is directly related to wind speed expressed in equation (18)
is directly related to wind speed expressed in equation (18)
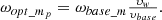 (18)
(18)
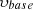 refers to the reference wind speed,
refers to the reference wind speed, 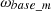 represents the rotor speed at the reference wind speed,
represents the rotor speed at the reference wind speed, 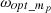 indicates the current optimal generator speed, and
indicates the current optimal generator speed, and 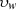 represents the current wind speed.
represents the current wind speed.
The control system will make significant corrections to the rotor speed when it changes from the required optimal speed. If the rotor speed gets closer to the required level the adaptive ratio 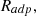 will decrease until the optimal speed is achieved and maintained as shown in equation (19)
will decrease until the optimal speed is achieved and maintained as shown in equation (19)
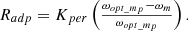 (19)
(19)
The perturbation constant 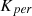 determines the degree of accuracy in achieving maximum power output. Figure 7 presents the variation in output power of wind turbines with respect to turbine speed.
determines the degree of accuracy in achieving maximum power output. Figure 7 presents the variation in output power of wind turbines with respect to turbine speed.
 |
Figure 7 Turbine speed VSs output power. |
The flowchart presented in Figure 6 defines the adaptive step P&O MPPT algorithm. After the algorithm determines the ideal rotor speed, a PI controller comes into play to produce a reference torque aimed at keeping the PMSG rotor at its optimal speed (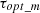 ). Following this, the input current reference (
). Following this, the input current reference (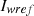 ) for the DC-DC converter can be evaluated from the torque reference as in equation (20).
) for the DC-DC converter can be evaluated from the torque reference as in equation (20).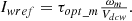 (20)
(20)
A DC current regulator with PI control is employed to maintain the output voltage of the DC-DC converter. This regulator generates the necessary duty cycle to control the IGBT switch. Figure 8 depicts the wind system incorporating the DC-DC converter. The output of the 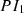 controller is reference torque
controller is reference torque 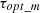 which is given as in equation (21)
which is given as in equation (21)
 (21)
(21)
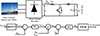 |
Figure 8 Wind generation system with boost converter. |
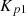 and
and 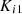 are PI controller gains.
are PI controller gains.
Output of the 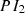 controller is the duty cycle (
controller is the duty cycle (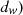 required by the converter which is given as
required by the converter which is given as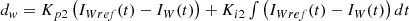 (22)
(22)
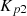 and
and  are PI controller gains.
are PI controller gains.
3.3 Battery energy storage system (BESS)
The battery’s behaviour can be described by its state of charge (SoC) expressed as a percentage, which is linked to the battery’s energy level, denoted as 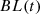 at a given time expressed in equation (23)
at a given time expressed in equation (23)
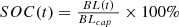 (23)
(23)
subjected to as in equation (24)
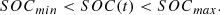 (24)
(24)
Here, 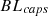 represents the battery’s initial nominal capacity, while
represents the battery’s initial nominal capacity, while 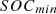 and
and 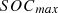 denote the upper and lower bounds of the battery’s SoC, respectively. These limits are established to minimize the impact of battery ageing and, consequently, to prolong the battery’s lifespan. Figure 9 depicts the utilization of a DC-DC converter and a VSI for connecting the battery to the AC bus.
denote the upper and lower bounds of the battery’s SoC, respectively. These limits are established to minimize the impact of battery ageing and, consequently, to prolong the battery’s lifespan. Figure 9 depicts the utilization of a DC-DC converter and a VSI for connecting the battery to the AC bus.
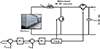 |
Figure 9 Battery storage system with DC-DC converter. |
The PI controller generates the duty cycle of the two switches, within the bidirectional DC-DC converter. According to Figure 9, the output of the  controller is reference battery current
controller is reference battery current 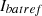 which is given as in equation (25),
which is given as in equation (25),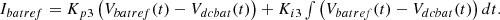 (25)
(25)
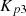 and
and 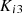 are PI controller gains,
are PI controller gains,  battery reference voltage,
battery reference voltage, 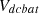 actual battery voltage (Figure 10).
actual battery voltage (Figure 10).
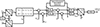 |
Figure 10 Control strategy of the DC–AC converter. |
Output of the 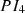 controller is the duty cycle of the switches in the bidirectional converter which is given as in equation (26)
controller is the duty cycle of the switches in the bidirectional converter which is given as in equation (26)
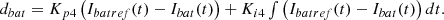 (26)
(26)
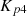 and
and 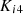 are PI controller gains,
are PI controller gains,  battery reference current,
battery reference current, 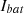 actual battery current.
actual battery current.
4 Current control strategy of DC–AC converter
The active and reactive power controller introduces four PI controllers to enable regulated active and reactive power delivery to the load. These controllers manage the power flow between the grid and the utility.
Equations (27) and (28) showcase the reference current utilized for achieving the control objective. The two PI controllers within the power controller establish communication with the external control loop to generate the reference current vectors 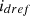 and
and 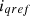 .
.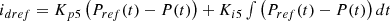 (27)
(27)
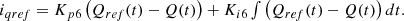 (28)
(28)
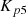 and
and 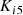 are PI controller gains,
are PI controller gains, 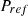 reference active power,
reference active power, 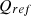 reference reactive power,
reference reactive power, 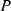 actual active power and
actual active power and  actual reactive power.
actual reactive power.
The controller’s output is crucial to ensure precise tracking and minimize inverter ripple. This objective is accomplished by employing two PI controllers to eliminate current errors, along with an inverter current feedback and grid voltage feedforward loop, which enhances both steady-state and dynamic performance. The controller employs a PWM system to generate voltage vectors with reduced harmonic distortion. Besides the PWM system, the controller incorporates a current feedback loop and a grid voltage feedforward loop to improve steady-state and dynamic performance. These loops are used to remove current errors, achieve precise tracking, and minimize inverter drift as can be seen in equations (29) and (30).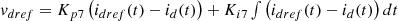 (29)
(29)
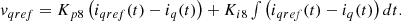 (30)
(30)
 and
and 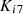 are PI controller gains,
are PI controller gains, 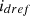 reference direct axis current,
reference direct axis current, 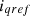 reference quadrature axis current,
reference quadrature axis current, 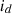 actual direct axis current and
actual direct axis current and 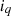 actual quadrature axis current.
actual quadrature axis current.
During grid-connected mode, the HDGS unit controls both the magnitude and phase angle of the inverter current to deliver the predetermined active and reactive power values to the grid. The control strategy for active and reactive power in the HDGS unit relies on frequency and voltage regulation. Evaluating the performance of the HDGS unit involves considering the outputs of the PV irradiance, wind turbine, and battery.
Tuning PI controller gains is essential to ensure effective and stable control of a system. PI controllers are commonly used in control systems to regulate a process variable. Heuristic optimization algorithms can be employed to automate the tuning process of a PI controller. These algorithms explore the parameter space, searching for optimal controller settings that minimize a performance metric such as integral of time-weighted absolute error (ITAE), overshoot, or settling time. When applying heuristic optimization algorithms to PI controller tuning, it’s essential to define the objective function based on the specific control system’s performance criteria. Additionally, the algorithm parameters (e.g., population size, and mutation rate) should be carefully selected and tuned for the application. It’s often beneficial to run multiple optimization trials and analyse the results to ensure robustness and reliability in achieving optimal controller settings.
The objective of design optimization is to identify the optimal design by minimizing an objective function, adjusting design variables, and adhering to specified design constraints. When undertaking design optimization, it is common to encounter scenarios where multiple design criteria or objective functions must be considered simultaneously. In such instances, the design problem transforms into a multi-objective optimization challenge.
In contrast to conventional optimization methods tailored for scalar objective functions, the approach to multi-objective optimization differs significantly. Traditional methods that focus on a single objective function are inadequate for handling the complexity and nuances associated with optimizing multiple, potentially conflicting objectives simultaneously. Therefore, specialized multi-objective optimization techniques become essential in addressing the intricacies of these multifaceted design problems.
Multi-objective optimization can be defined as shown in equations (31)–(34)
![$$ \begin{array}{c}\mathrm{min}F\left(x,k\right)={\left[{F}_1\enspace {F}_2\dots {F}_n\right]}^T\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq132.gif) (31)
(31)
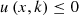 (32)
(32)
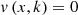 (33)
(33)
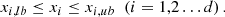 (34)
(34)
Consider the objective function vector 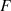 , which is a function of the design vector
, which is a function of the design vector  and a constant parameter vector
and a constant parameter vector 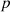 . The inequality and equality constraints are denoted by
. The inequality and equality constraints are denoted by  and
and  respectively. Additionally,
respectively. Additionally, 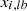 and
and 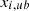 represent the lower and upper bounds for the
represent the lower and upper bounds for the  th design variable. The predominant approach for multi-objective optimization is the weighted sum method. This method involves integrating multiple objectives into a unified scalar objective function. It achieves this by assigning a weighting factor to each objective function and computing their sum. In essence, the transformed scalar objective function is a weighted combination of the individual objective functions, facilitating a consolidated optimization criterion highlighted as
th design variable. The predominant approach for multi-objective optimization is the weighted sum method. This method involves integrating multiple objectives into a unified scalar objective function. It achieves this by assigning a weighting factor to each objective function and computing their sum. In essence, the transformed scalar objective function is a weighted combination of the individual objective functions, facilitating a consolidated optimization criterion highlighted as 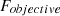 in equation (35).
in equation (35).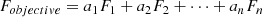 (35)
(35)
Where 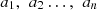 are the weights of the respective objective functions. If
are the weights of the respective objective functions. If 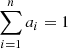 and
and 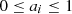 , the weighted sum is characterized as a convex combination of objectives. In this scenario, each optimization focusing on a single objective identifies a specific optimal solution point along the Pareto front. The weighted sum method subsequently varies weights systematically, resulting in distinct single-objective optimizations that yield different optimal solutions.
, the weighted sum is characterized as a convex combination of objectives. In this scenario, each optimization focusing on a single objective identifies a specific optimal solution point along the Pareto front. The weighted sum method subsequently varies weights systematically, resulting in distinct single-objective optimizations that yield different optimal solutions.
In this work, the optimization of PI controller gains is achieved by adopting the Integral of Time-weighted Absolute Error (ITAE) as the single objective function. The objective function to be minimized is formulated as the sum of the integral of the absolute error multiplied by time for each individual PI controller. The optimization goal is to minimize this aggregated ITAE, thereby enhancing the dynamic response and overall performance of the control system. The final objective function that should be minimised is given in equation (36)
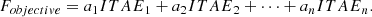 (36)
(36)
The Enhanced Randomized Harris Hawk Optimization algorithm is employed as the optimization technique for determining the optimal Proportional-Integral (PI) controller gains (proportional gain and integral time constant). This optimization process aims to enhance the dynamic response of the system. The goal is to optimize all eight PI controller gains (Two PI controllers are responsible for regulating the boost converter in the wind generation system, another two PI controllers govern the bidirectional converter in the battery storage system and the remaining four PI controllers operate within the DC–AC converter) within the control system, aiming to achieve improved control over active and reactive power, as well as enhanced regulation of DC and AC side voltages. The PI controller gains subject to optimization include 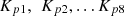 , representing the eight proportional gains, along with
, representing the eight proportional gains, along with 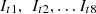 , which signify the integral time constants.
, which signify the integral time constants.
5 Harris Hawks algorithm (HHO)
The HHO algorithm draws inspiration from the various hunting strategies employed by hawks when searching for and capturing their hunt. HHO is a particle-based optimization technique composed of 3 distinct steps: exploration, transformation, and exploitation.
5.1 Exploration stage
During this stage, hawks select random perching locations, influenced by the positions of other group members or the locations of rabbits. This behaviour is modelled as shown in equations (37) and (38)
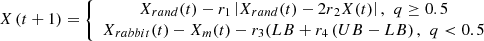 (37)
(37)
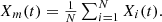 (38)
(38)
In this context, 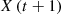 signifies the forthcoming location of hawks in the subsequent cycles, where
signifies the forthcoming location of hawks in the subsequent cycles, where 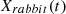 denotes the prey’s current location, X(t) represents the current positions of the hawks.
denotes the prey’s current location, X(t) represents the current positions of the hawks. 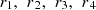 , and q denote random numbers within the range (0, 1).
, and q denote random numbers within the range (0, 1). 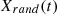 corresponds to the location of a randomly chosen member from the hawk and
corresponds to the location of a randomly chosen member from the hawk and 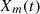 indicates the mean value of the location of hawks.
indicates the mean value of the location of hawks.
5.2 Transformation
The prey’s escape energy plays a crucial role in the intermediate stage, and it is assessed using equations (39) and (40).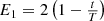 (39)
(39)
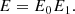 (40)
(40)
“t” represents the present iteration, “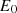 ” denotes the initial prays energy, which varies within the random range of −1 to 1, and “T” represents the maximum number of iterations.
” denotes the initial prays energy, which varies within the random range of −1 to 1, and “T” represents the maximum number of iterations.
5.3 Exploitation stage
In this phase, the hawks engage in pursuit of the prey, employing four distinct hunting approaches and considering the prey’s diverting behaviour. A successful capture hinges on two factors: the escaping energy (E) and the escape potential (r). The variable escape potential (r) is a random number in the range of 0 to 1.
When r is equal to or greater than 0.5, and the absolute value of the escaping energy (|E|) is also equal to or greater than 0.5, the hawks initiate a soft besiege as defined by equations (41) and (42). This signifies that the prey possesses sufficient energy but their attempt to escape has been unsuccessful. (41)
(41)
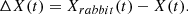 (42)
(42)
Here, ΔX(t) indicates the difference between the positions of the hawks at iteration t and the present location of the prey. Additionally, 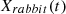 denotes the leap strength, which undergoes random variation with each iteration. When r is greater than or equal to 0.5, and the absolute value of the escaping energy (|E|) is less than 0.5 then,
denotes the leap strength, which undergoes random variation with each iteration. When r is greater than or equal to 0.5, and the absolute value of the escaping energy (|E|) is less than 0.5 then, 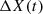 is given as in equation (43).
is given as in equation (43).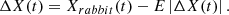 (43)
(43)
When the escape potential (r) is less than 0.5, and the absolute value of escaping energy (|E|) is equal to or greater than 0.5, hawks employ a more calculated, gentle encirclement strategy known as “hard besiege” with gradually intensifying swift dives. This behaviour is detailed as shown in equations (44) and (45).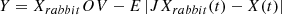 (44)
(44)
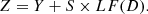 (45)
(45)
Here, “D” represents the dimension of the problem, “S” represents a random matrix with an order of 1 × D, “LF” stands for the Levy flight relation, as given in equations (46) and (47).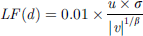 (46)
(46)
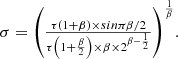 (47)
(47)
The process of updating the positions of the hawks can be represented through the following equation (48), wherein “u” and “v” are vectors with an order of 1 × d, “β” is a constant in the range of 0 to 1.5, and  represents the Gamma function.
represents the Gamma function.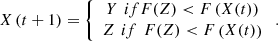 (48)
(48)
In cases where the prey’s energy is completely consumed, a robust besiege is initiated, indicated by the conditions when “r” is less than 0.5 and the absolute value of “E” is less than 0.5. The computation of “Y”, “Z” is illustrated in equations (49) and (50).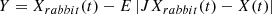 (49)
(49)
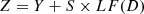 (50)
(50)
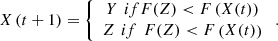 (51)
(51)
6 Proposed algorithm
6.1 Tent chaotic map
Over recent years, several researchers have demonstrated the effectiveness of chaotic maps [28] in enhancing the hunting capabilities of particle-based algorithms. Typically, chaotic maps are incorporated into one or more phases of these algorithms, including the initial population generation, exploration, or exploitation stages. The way locations are initialized has a significant impact on both the population’s diversity and the algorithm’s stability. While the ERHHO algorithm can ensure the randomness of the s particles position during initialization. Chaotic sequences possess unpredictability and randomness. Chaotic mappings can initialize random numbers that follow in the range of 0 and 1. The features and randomness of this map can enhance performance by altering the starting positions of hawks which is given in equation (52)
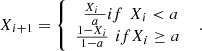 (52)
(52)
In this equation, 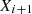 is the new location of the hawks after applying chaotic mapping,
is the new location of the hawks after applying chaotic mapping, 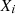 denotes the hawks’ position, and “a” is set to 0.8.
denotes the hawks’ position, and “a” is set to 0.8.
6.2 Exploration factor
During the exploration step, the ERHHO primarily calculates position updates using equations (37) and (38), where r1 and r3 represent random values within the limits of 0 and 1. While these locations introduce randomness into every iteration of the overall exploration, they may lack the desired adaptability. The conventional HHO models a scenario where hawks may effectively chase and identify their prey. However, there are occasions when the prey is not easily visible, and hawks might take several hours to detect their target.
The parameters r1 and r3 can be regarded as the step length, where larger values make hawks move more quickly, and conversely, smaller values result in slower movement. There are two distinct scenarios for hawks finding their prey: immediate detection and long-term search. In the first scenario, it’s essential to consider randomness in the length of iteration. In contrast, in the next situation, the step length should decrease. Since the probability of a hawk spotting prey rises over time, hawks must initially search in a widespread limit with larger steps, and then transition to a more precise search in the later iterations. Exploration factor (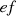 ) is given as in equation (53)
) is given as in equation (53)
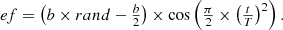 (53)
(53)
The value of “b” is set to 2, which has been determined to yield satisfactory results through experimental testing. The term 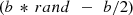 is presented to introduce step length randomness by producing random numbers within the range of (−b/2, b/2). The cosine relation is employed to create a non-linear convergence, transitioning from 1 to 0 with each iteration.
is presented to introduce step length randomness by producing random numbers within the range of (−b/2, b/2). The cosine relation is employed to create a non-linear convergence, transitioning from 1 to 0 with each iteration.
Then equation (37) is simplified as in equation (54)
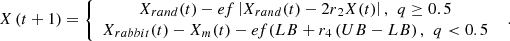 (54)
(54)
Enhancing Exploration in Optimization Algorithms: The Role of the Exploration Factor.
In optimization algorithms, the exploration factor plays a critical role in determining the search behaviour during the iterative process. At the outset of the optimization process, the exploration factor widens the permissible range of step lengths. Initially, the step lengths are confined to the interval (0, 1). However, the exploration factor introduces a shift, expanding the limits to (−b/2, b/2). This adjustment allows for more extensive exploration during the early iterations. As the optimization algorithm progresses, the exploration process evolves. Initially, the broader exploration range allows the algorithm to explore a wide variety of solutions. As the number of iterations increases, the exploration factor gradually narrows the step length limits. Consequently, the algorithm transitions from broad exploration to finer exploration. Fine exploration focuses on smaller regions of the optimization space, aiming for precision and convergence toward optimal solutions. Despite the narrowing of step length limits, the exploration factor ensures that randomness is preserved. Randomness is essential for escaping local optima and discovering global optima. By maintaining some degree of randomness in step lengths, the algorithm avoids getting stuck in suboptimal regions.
6.3 Random walk strategy
During the exploitation stage of the HHO algorithm, hawks update their positions using four search strategies. While this boosts exploration, proceeding to the next iteration without interference can lead the algorithm to be stuck in local optima. To mitigate this, common strategies like the Gaussian random walk, Levy flight, and Brownian motion [29] are applied. These strategies tend to stabilize within certain value ranges with high probability but can experience substantial changes with low probability, introducing a level of deviation to the methods.
When the fitness value is the same as in the previous iteration, this step can be initiated which induces a deviation in the location of a hawk based on a changing parameter calculated as 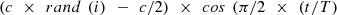 and declines as reiterations progress. This can be defined as in equation (55)
and declines as reiterations progress. This can be defined as in equation (55)
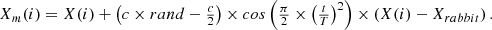 (55)
(55)
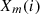 represents the latest location after implementing the random walk strategy. To ensure that the effective result is retained and carried forward into the next iteration, a greedy strategy is employed, which is detailed in equation (56)
represents the latest location after implementing the random walk strategy. To ensure that the effective result is retained and carried forward into the next iteration, a greedy strategy is employed, which is detailed in equation (56)
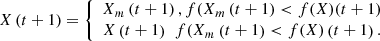 (56)
(56)
6.4 The details of ERHHO
The ERHHO algorithm focuses on refining certain aspects of HHO [36]. While HHO is effective in local exploitation, it tends to lack in total exploration. ERHHO addresses this by linking the transition from exploration to exploitation to the prey’s energy. In the initial iterations representing the exploration phase, the range of particles is typically inadequate, leading to a slower convergence rate. As iterations progress, the energy of the prey decreases, and the algorithm enters a phase of local exploitation.
To adapt to these changing conditions, ERHHO employs four distinct hunting techniques depending on the energy of the prey and the probability of escaping. Hence, the tent chaotic map is added to augment the particle’s diversity. The fine-tuned crucial parameters during the exploration phase using the exploration factor. As part of the exploitation step, incorporated a random walk strategy to improve the capability to escape local optima. These combined approaches enhance both the convergence speed and accuracy, effectively elevating the overall optimization performance of the program. ERHHO comprises three fundamental components: initialization, location updating, and fitness estimation. The generation of locations involves an algorithmic complexity of O(N∗D), with N representing the particle size and D representing the problem’s dimensions. Fitness solution evaluation takes O(N) computational effort. To safeguard against local optima, incorporated a random walk strategy, increasing the mathematical complexity to O (2 × N × D × T), where T represents the number of iterations. Consequently, the total computational complexity of the proposed ERHHO algorithm is O (2 × N × D × T). A detailed flowchart for the ERHHO optimization is shown in Figure 11.
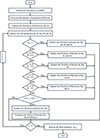 |
Figure 11 Flowchart of the ERHHO optimization. |
Steps involved in optimization.
-
Defining the objective function that quantifies the performance of the microgrid.
-
Initialize a population of potential solutions (candidate sets of PI controller gains) using the ERHHO algorithm. This typically involves randomly generating a set of potential gain values within the specified bounds.
-
Evaluate the fitness of each candidate solution by applying the corresponding PI controller gains to the microgrid model and simulating its performance under various operating conditions and scenarios. The fitness function assesses how well the controller achieves the desired control objectives.
-
The ERHHO algorithm iteratively explores the solution space, updating the candidate solutions based on their fitness values. It employs a combination of exploration (random search) and exploitation (local search) strategies to converge towards optimal or near-optimal solutions. At each iteration, the algorithm perturbs the solutions, evaluates their fitness, and updates them accordingly.
-
The optimization process continues for a predefined number of iterations or until a termination criterion is met, such as reaching a specified level of convergence or exceeding a maximum number of function evaluations.
-
Once the optimization process is complete, extract the best solutions found by the ERHHO algorithm, corresponding to the optimal PI controller gains for the microgrid.
7 Simulation results
This section is dedicated to presenting simulation results that aim to establish the credibility and efficacy of the proposed control method ERHHO. A key performance metric involves assessing the method’s ability is to maintain the DC bus voltage, as well as active and reactive powers within specified ranges across various Microgrid (MG) operational modes. The efficacy of the proposed control is illustrated through simulation results conducted within the MATLAB/SIMULINK environment. Table 1 presents the specifications of the system adopted for simulation results. To establish the superiority of the developed methodology based on Enhanced Randomized Harris Hawk Optimization (ERHHO), a comparative analysis is performed against outcomes obtained using Monte Carlo Artificial Bee Colony Optimization (MCABC) [30], Hybrid Teaching Learning Based Optimization and Equilibrium Optimizer (TLBO-EO) [31], Enhanced Slime Mold Optimization Algorithm (SMO) [32], Artificial Rabbits Algorithm (ARA) [33], Coot Bird Metaheuristic Optimizer (CB) [34], and Ziegler-Nichols (ZN) [35]. The control strategy outlined in Section 3 is implemented for the system presented in Figure 1. The simulation involves the utilization of PI gains that have been optimized through the proposed algorithm. Optimized gains by the proposed algorithm and various algorithms from the literature are presented in Table 2. Three cases are considered to check the efficacy of the optimized PI gains by the proposed algorithm: reference active and reactive power change, irradiance and wind speed variation, and isolation of PV and wind generation systems.
Parameters of the Hybrid DG system.
Optimized gains of PI controllers using proposed and various algorithms.
Case 1: Reference Active and Reactive Power change. In this case, dynamic changes in active and reactive power references (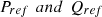 ) are examined over specific time intervals. These references are adjusted as follows: from 0 to 4 s,
) are examined over specific time intervals. These references are adjusted as follows: from 0 to 4 s, 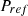 is set to 300 kW and
is set to 300 kW and  to 250 kVAR; from 4 to 8 s, then increased to 400 kW and 350 kVAR; from 8 to 12 s, a further increase is observed to 600 kW and 550 kVAR; from 12 to 16 s, a reduction to 350 kW and 300 kVAR occurs, and from 16 to 20 s, stabilize at 300 kW and 200 kVAR. The connected load remains constant at 500 kW and 400 kVAR. Additionally, the environmental inputs for the PV system include an irradiance of 1000 W/m² and a temperature of 35 °C, while the wind speed input for the wind generation system is set at 12 m/s. The comparison in tracking efficiency of the microgrid, employing optimized Proportional-Integral (PI) controller gains through Enhanced Randomized Harris Hawk Optimization (ERHHO) and other algorithms (MCABC, TLBO-EO, SMO, ARA, CB, and ZN), is depicted in Figure 12. For a more detailed examination, Figures 13 and 14 offer better visualization of the injected active and reactive powers by the microgrid between 0 to 1 s and 11.6 to 13 s, respectively. Figure 16 provides the active and reactive power supplied to the load by the PV-wind-battery system. Figure 17 specifics the active and reactive powers provided by the grid. Notably, between 8 and 12 s, any excess power generated by the PV-wind-battery system, beyond what is needed by the load, is absorbed by the grid. The generated power by the PV and wind sources is presented in Figure 18. With an irradiance of 1000 w/m2 generated power from PV is 143.6 kW and with a wind speed of 12 m/s generated power from the wind generation system is 145.25 kW. Simultaneously, Figure 19 illustrates the DC link voltage of the DC bus before the DC–AC converter. The efficiency of DC link voltage tracking is compared between the proposed algorithm and previous algorithms in Figures 20 and 21, specifically during the time intervals 0–1 s and 3–6 s. To numerically quantify the comparison, Table 3 provides metrics such as rise time, peak overshoot, settling time, and steady-state error for DC bus voltage, active power, and reactive power. Table 4 presents performance indices, including Integral Absolute Error (IAE), Integral Square Error (ISE), Integral Time Absolute Error (ITAE), and Integral Time Squared Error (ITSE). IAE is the cumulative absolute error over time, and it signifies the response speed and oscillations during stability conditions. IAE is 0.0204, 0.0176 and 0.0179 for DC voltage regulation, active and reactive power respectively. Compared to its nearest optimization algorithm, the proposed algorithm achieved 40–60% of less IAE indicating improved performance. ISE quantifies the cumulative squared error over time, and it provides a balance between overshoot and settling time. ISE is 0.0109, 0.0113 and 0.0111 for DC voltage regulation, active and reactive power respectively. ITSE integrates the absolute error multiplied by time over time and this value defines the Balance between response speed and error magnitude. ITSE is 0.0042, 0.002, and 0.0024 for DC voltage regulation, active and reactive power respectively. ITAE integrates the absolute error multiplied by time and it emphasizes minimizing error during transient response. ITAE is 0.000092, 0.00008 and 0.000081 for DC voltage regulation, active and reactive power respectively. This detailed analysis and comparison aim to offer a comprehensive understanding of the microgrid’s performance under varying conditions and the efficacy of the ERHHO algorithm in optimizing PI controller gains (Figure 15).
to 250 kVAR; from 4 to 8 s, then increased to 400 kW and 350 kVAR; from 8 to 12 s, a further increase is observed to 600 kW and 550 kVAR; from 12 to 16 s, a reduction to 350 kW and 300 kVAR occurs, and from 16 to 20 s, stabilize at 300 kW and 200 kVAR. The connected load remains constant at 500 kW and 400 kVAR. Additionally, the environmental inputs for the PV system include an irradiance of 1000 W/m² and a temperature of 35 °C, while the wind speed input for the wind generation system is set at 12 m/s. The comparison in tracking efficiency of the microgrid, employing optimized Proportional-Integral (PI) controller gains through Enhanced Randomized Harris Hawk Optimization (ERHHO) and other algorithms (MCABC, TLBO-EO, SMO, ARA, CB, and ZN), is depicted in Figure 12. For a more detailed examination, Figures 13 and 14 offer better visualization of the injected active and reactive powers by the microgrid between 0 to 1 s and 11.6 to 13 s, respectively. Figure 16 provides the active and reactive power supplied to the load by the PV-wind-battery system. Figure 17 specifics the active and reactive powers provided by the grid. Notably, between 8 and 12 s, any excess power generated by the PV-wind-battery system, beyond what is needed by the load, is absorbed by the grid. The generated power by the PV and wind sources is presented in Figure 18. With an irradiance of 1000 w/m2 generated power from PV is 143.6 kW and with a wind speed of 12 m/s generated power from the wind generation system is 145.25 kW. Simultaneously, Figure 19 illustrates the DC link voltage of the DC bus before the DC–AC converter. The efficiency of DC link voltage tracking is compared between the proposed algorithm and previous algorithms in Figures 20 and 21, specifically during the time intervals 0–1 s and 3–6 s. To numerically quantify the comparison, Table 3 provides metrics such as rise time, peak overshoot, settling time, and steady-state error for DC bus voltage, active power, and reactive power. Table 4 presents performance indices, including Integral Absolute Error (IAE), Integral Square Error (ISE), Integral Time Absolute Error (ITAE), and Integral Time Squared Error (ITSE). IAE is the cumulative absolute error over time, and it signifies the response speed and oscillations during stability conditions. IAE is 0.0204, 0.0176 and 0.0179 for DC voltage regulation, active and reactive power respectively. Compared to its nearest optimization algorithm, the proposed algorithm achieved 40–60% of less IAE indicating improved performance. ISE quantifies the cumulative squared error over time, and it provides a balance between overshoot and settling time. ISE is 0.0109, 0.0113 and 0.0111 for DC voltage regulation, active and reactive power respectively. ITSE integrates the absolute error multiplied by time over time and this value defines the Balance between response speed and error magnitude. ITSE is 0.0042, 0.002, and 0.0024 for DC voltage regulation, active and reactive power respectively. ITAE integrates the absolute error multiplied by time and it emphasizes minimizing error during transient response. ITAE is 0.000092, 0.00008 and 0.000081 for DC voltage regulation, active and reactive power respectively. This detailed analysis and comparison aim to offer a comprehensive understanding of the microgrid’s performance under varying conditions and the efficacy of the ERHHO algorithm in optimizing PI controller gains (Figure 15).
 |
Figure 12 Active and reactive power provided by PV-WIND and battery system. |
 |
Figure 13 Active and reactive power provided by PV-WIND and battery system from 0 to 1 s. |
 |
Figure 14 Active and reactive power provided by PV-WIND and battery system from 11.6 to 13 s. |
 |
Figure 15 Active and reactive power provided by PV-WIND and battery system with proposed ERHHO. |
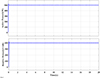 |
Figure 16 Load active and reactive power. |
 |
Figure 17 Grid active and reactive power. |
 |
Figure 18 PV and wind generated power. |
 |
Figure 19 DC bus voltage. |
 |
Figure 20 DC bus voltage comparison from 0 to 1 s. |
 |
Figure 21 DC link voltage comparison from 3.9 to 6 s. |
Comparison of metrics between proposed algorithm and previous algorithms from the literature.
Comparison of performance indices between proposed algorithm and previous algorithms from literature.
Figures 13 and 14 provide clearer visualizations of injected active and reactive powers during critical time intervals. ERHHO ensures more precise and stable power injection, contributing to enhanced overall microgrid performance. In Figure 16, ERHHO optimally manages the active and reactive power supplied to the load by the PV-wind-battery system, as well as the interaction with the grid. Notably, between 8 and 12 s, ERHHO effectively regulates excess power, demonstrating improved control over power flow and grid interaction compared to other algorithms. Figures 19, 20, and 21 showcase the superior performance of ERHHO in maintaining stable DC link voltage. Particularly during critical time intervals (0–1 s and 3–6 s), ERHHO ensures precise tracking, minimizing deviations and outperforming alternative algorithms. Table 3 provides numerical metrics, including rise time, peak overshoot, settling time, and steady-state error for DC bus voltage, active power, and reactive power. ERHHO consistently yields better results across these metrics compared to the other optimization algorithms. Table 4 highlights the performance indices, including Integral Absolute Error (IAE), Integral Square Error (ISE), Integral Time Absolute Error (ITAE), and Integral Time Squared Error (ITSE). ERHHO excels in minimizing these performance indices, indicating superior optimization in terms of system response and stability. The proposed ERHHO algorithm demonstrates notable advancements in optimizing PI controller gains for the microgrid compared to existing optimization algorithms. It provides enhanced tracking efficiency, more stable power injection, improved regulation of load power supply and grid interaction, and superior stability in DC link voltage. The quantitative comparisons further validate ERHHO’s effectiveness in optimizing the microgrid’s control system for various operational scenarios.
Case 2: In this case, the effectiveness of optimized Proportional-Integral (PI) gains in ensuring continuous power supply to the load is investigated by considering alterations in irradiance and wind speed. The changes in irradiance are detailed as follows: from 0 to 3.5 s, it is 400 W/m²; from 3.5–7 s, it increases to 600 W/m²; from 7 to 10.5 s, it further rises to 800 W/m²; from 10.5 to 14 s, it peaks at 1000 W/m²; from 14 to 17.5 s, it decreases to 750 W/m², and from 17.5 s onward, it stabilizes at 550 W/m². Simultaneously, the wind speed experiences variations: from 0 to 3 s, it is 9 m/s; from 3 to 8 s, it increases to 11 m/s; from 8 to 12 s, it further rises to 12 m/s; from 12 to 17 s, it peaks at 13 m/s, and from 17 s onward, it decreases back to 9 m/s. this variation of irradiance and wind speed is presented in Figure 22. Figure 23 illustrates the corresponding changes in generated power from the Photovoltaic (PV) and wind sources. For irradiance of 400 W/m2 generated power from PV is 59.84 kW, it increased to 90.27 kW when irradiance is 600 W/m2, again increased to 120.3 kW when irradiance is 800 W/m², and 143.6 kW when irradiance is 1000 W/m². The wind generation system generates the powers of 109.1 kW, 133.3 kW, 145.4 kW and 157.52 kW when wind speed is 9 m/s, 11 m/s, 12 m/s and 13 m/s respectively. Figure 24 provides a comprehensive overview of the reference and actual active and reactive powers injected by the PV-wind-battery system. Reference active and reactive powers are reduced to 100 kW and 50 kVAR between 12 and 16 s. Consequently, the injected powers by the converter are adjusted to match these reference values. This reduction in injected power by the converter is effectively managed by the grid, ensuring the maintenance of constant load active and reactive powers, as depicted in Figure 25. The active and reactive power profiles of the grid are showcased in Figure 26. During the period between 12 and 16 s, the surplus power generated by the PV and wind sources that are not directed to the grid is efficiently stored in the battery, as evidenced by Figure 27. As the battery undergoes charging, the State of Charge (SOC) experiences an increase during this timeframe. Figure 28 presents the behaviour of the DC bus voltage throughout the analysed duration. The detailed examination of these figures underscores the intricate interplay between variations in irradiance and wind speed, the response of the PV-wind-battery system, and the adaptability of the grid and battery in maintaining a stable and continuous power supply to the load.
 |
Figure 22 Irradiance and wind speed change in PV and wind generation system. |
 |
Figure 23 PV and wind generated power. |
 |
Figure 24 Active and reactive power provided by PV-WIND and battery system with proposed ERHHO. |
 |
Figure 25 Load active and reactive power. |
 |
Figure 26 Grid active and reactive power. |
 |
Figure 27 Battery terminal power and SOC. |
 |
Figure 28 DC bus voltage. |
Case 3. In this case, PV and wind generation system powers are reduced to zero by disconnecting them from the HDGS to check the efficacy of the proposed optimization in providing continuous supply to the load. The PV and wind generation are disconnected from the overall power system during two distinct time intervals: first, from 3 to 7 s, and second, from 8 to 12 s, as visually represented in Figure 29. Throughout these periods, the remaining power essential for the DC to AC converter to follow reference values is supplemented by the battery system, as illustrated in Figure 30. The initial SOC of the battery is chosen as 50% and as the battery is in discharging mode SOC starts decreasing from 50%. This approach allows for a dynamic management of power sources, ensuring that the DC to AC-converter receives the necessary power support from the battery during the isolated periods of PV and wind generation.
 |
Figure 29 PV and wind generated power. |
 |
Figure 30 Battery terminal power and SOC. |
The proposed algorithm demonstrates significant improvements over several other optimization algorithms, including MCABC, TLBO-EO, SMO, ARA, CB, and ZN. The microgrid, equipped with the ERHHO-optimized Proportional-Integral (PI) controller gains, exhibits superior accuracy in following dynamic changes in active and reactive power references compared to the alternative optimization algorithms.
8 Conclusion
This paper presents a novel and effective approach to enhance the control strategies of microgrids, specifically focusing on the integration of renewable energy sources such as photovoltaic (PV) and wind generation. The utilization of a power flow control strategy and the proportional-integral (PI) controller within the microgrid framework is crucial for ensuring optimal performance under varying operating conditions. However, tuning the PI controller parameters poses a challenge due to the dynamic and nonlinear nature of renewable energy sources. To address this challenge, proposed the application of the Enhance Randomized Harris Hawk Optimization (ERHHO) algorithm for fine-tuning the PI controller. Utilizing the ERHHO algorithm’s ability to mimic the hunting behaviour of hawks in finding optimal solutions, demonstrated its efficacy in navigating the complex solution space and converging to optimal PI controller settings. This optimization contributes to the microgrid’s dynamic behaviour, particularly in the context of diverse renewable energy sources. The comprehensive simulations conducted in this study evaluate the effectiveness of the proposed Enhance Randomized Harris Hawk Optimization-based PI controller tuning. Performance metrics such as transient response, overshoot, settling time, and steady-state error are analysed to validate the robustness and efficiency of the proposed method. Compared to its nearest optimization algorithm MCABC, with the proposed algorithm rise time is reduced by 50%, overshoot is reduced by 75%, settling time is reduced by 66%, and finally, the percentage of reduction of steady-state error is 45%. Rise time is 0.0254, 0.0199, and 0.0199 s for DC voltage, active and reactive power respectively. Steady-state error is 0.3389, 0.1587, and 0.0355 for DC voltage, active and reactive power. The results of this research mark a significant advancement in microgrid control strategies, offering a promising avenue for PI controller tuning in the presence of various renewable energy sources. The integration of the Enhance Randomized Harris Hawk Optimization algorithm proves to be a valuable tool in enhancing the operational efficiency and reliability of microgrids. This research contributes to the broader goal of establishing sustainable and resilient energy systems, crucial for addressing the evolving energy landscapes and growing demand for reliable and environmentally friendly energy solutions.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work, the author(s) used ChatGPT in order to proofread the manuscript. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.
References
- Sen S., Kumar V. (2018) Microgrid control: A comprehensive survey, Annu. Rev. Control 45, 118–151. [CrossRef] [MathSciNet] [Google Scholar]
- Chaudhary G., et al. (2021) Review of energy storage and energy management system control strategies in microgrids, Energies 14, 16, 4929. [CrossRef] [Google Scholar]
- Muqeet H.A., et al. (2022) Sustainable solutions for advanced energy management system of campus microgrids: Model opportunities and future challenges, Sensors 22, 6, 2345. [CrossRef] [PubMed] [Google Scholar]
- Hossain Md.A., et al. (2019) Evolution of microgrids with converter-interfaced generations: Challenges and opportunities, Int. J. Electr. Power Energy Syst. 109, 160–186. [CrossRef] [Google Scholar]
- Haseeb J., et al. (2021) Optimal energy management of a campus microgrid considering financial and economic analysis with demand response strategies, Energies 2021, 14, 8501. [Google Scholar]
- Bin L., et al. (2022) Scheduling and sizing of campus microgrid considering demand response and economic analysis, Sensors 22, 16, 6150. [CrossRef] [PubMed] [Google Scholar]
- Elnady A., et al. (2022) A comprehensive review of centralized current/power control schemes for parallel inverters and AC microgrids, IEEE Access 10, 125061–125085. [CrossRef] [Google Scholar]
- Kim H., et al. (2019) Direct energy trading of microgrids in distribution energy market, IEEE Trans. Power Syst. 35, 1, 639–651. [Google Scholar]
- Farzin H., et al. (2017) A market mechanism to quantify emergency energy transactions value in a multi-microgrid system, IEEE Trans. Sustain. Energy 10, 1, 426–437. [Google Scholar]
- Jumani T.A., et al. (2019) Optimal power flow controller for grid-connected microgrids using grasshopper optimization algorithm, Electronics 8, 1, 111. [CrossRef] [Google Scholar]
- Jumani T.A., et al. (2020) Swarm intelligence-based optimization techniques for dynamic response and power quality enhancement of AC microgrids: A comprehensive review, IEEE Access 8, 75986–76001. [CrossRef] [Google Scholar]
- Vishal V., et al. (2014) Online PI controller tuning for a nonlinear plant using genetic algorithm. In: 2014 Innovative Applications of Computational Intelligence on Power, Energy and Controls with their impact on Humanity (CIPECH), IEEE. [Google Scholar]
- Abdolrasol Maher G.M., et al. (2022) Optimal PI controller based PSO optimization for PV inverter using SPWM techniques, Energy Rep. 8, 1003–1011. [CrossRef] [Google Scholar]
- Ramasamy V., et al. (2023) A comprehensive review on Advanced Process Control of cement kiln process with the focus on MPC tuning strategies, J. Process Control 121, 85–102. [CrossRef] [Google Scholar]
- Jia L.Y., et al. (2023) A weighted-sum chaotic sparrow search algorithm for interdisciplinary feature selection and data classification, Sci. Rep. 13, 1, 14061. [CrossRef] [Google Scholar]
- Al-Betar M.A., et al. (2023) Economic load dispatch using memetic sine cosine algorithm, J. Ambient Intell. Human. Comput. 14, 9, 11685–11713. [CrossRef] [Google Scholar]
- Gupta S., Rong S. (2023) Diversity-enhanced modified sine cosine algorithm and its application in solving engineering design problems, J. Comput. Sci. 72, 102105. [CrossRef] [Google Scholar]
- Pham V.H.S., Nguyen Dang N.T., Nguyen V.N. (2023) Hybrid sine cosine algorithm with integrated roulette wheel selection and opposition-based learning for engineering optimization problems, Int. J. Comput. Intell. Syst. 16, 1, 171. [CrossRef] [Google Scholar]
- Mousa A.A., El-Shorbagy M.A., Farag M.A. (2020) Steady-state sine cosine genetic algorithm based chaotic search for nonlinear programming and engineering applications, IEEE Access 8, 212036–212054. [CrossRef] [Google Scholar]
- Chun Y., Hua X. (2023) Improved sine cosine algorithm for optimization problems based on self-adaptive weight and social strategy, IEEE Access. [Google Scholar]
- Alsoul M., et al. (2023) A new efficient hybrid approach for machine learning-based firefly optimization, Iraqi J. Sci. 4600–4612. [CrossRef] [Google Scholar]
- Patel C., Malakar T., Sreejith S. (2023) Assessment of converter performance in hybrid AC–DC power system under optimal power flow with minimum number of DC link control variables, Energies 16, 15, 5800. [CrossRef] [Google Scholar]
- Thiruvenkadam S., Kim H.-J., Ra I.-H. (2020) Hybrid fuzzy and flower pollination optimization algorithm for optimal dispatch of generating units in the existence of electric vehicles, in2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), IEEE. [Google Scholar]
- Alweshah M., et al. (2020) Flower pollination algorithm for solving classification problems, Int. J. Adv. Soft Comput. Appl. 12, 1, 15–34. [Google Scholar]
- Singh N., Kaur J. (2021) Hybridizing sine–cosine algorithm with harmony search strategy for optimization design problems, Soft Comput. 25, 16, 11053–11075. [CrossRef] [Google Scholar]
- Dashtaki A.A., et al. (2023) Optimal management algorithm of microgrid connected to the distribution network considering renewable energy system uncertainties, Int. J. Electr. Power Energy Syst. 145, 108633. [CrossRef] [Google Scholar]
- Fahim K.E., et al. (2023) A state-of-the-art review on optimization methods and techniques for economic load dispatch with photovoltaic systems: Progress, challenges, and recommendations, Sustainability 15, 15, 11837. [CrossRef] [Google Scholar]
- Wang Y., et al. (2023) Adaptive chimp optimization algorithm with chaotic map for global numerical optimization problems, J. Supercomput. 79, 6, 6507–6537. [CrossRef] [Google Scholar]
- Lawley S.D. (2023) Extreme statistics of superdiffusive Lévy flights and every other Lévy subordinate Brownian motion, J. Nonlinear Sci. 33, 4, 53. [CrossRef] [Google Scholar]
- Zamee M.A., Han D., Won D. (2023) Integrated grid forming-grid following inverter fractional order controller based on Monte Carlo artificial Bee Colony optimization, Energy Rep. 9, 57–72. [CrossRef] [Google Scholar]
- Sayed E.A., et al. (2023) Enhancement of PV performance by using hybrid TLBO-EO optimization, Ain Shams Eng. J. 14, 3, 101892. [CrossRef] [Google Scholar]
- Abid S., et al. (2023) Development of slime mold optimizer with application for tuning cascaded PD-PI controller to enhance frequency stability in power systems, Mathematics 11, 8, 1796. [CrossRef] [Google Scholar]
- El-Sehiemy R., et al. (2023) Proportional-integral-derivative controller based-artificial rabbits algorithm for load frequency control in multi-area power systems, Fractal Fract. 7, 1, 97. [CrossRef] [Google Scholar]
- Hussien A.M., et al. (2022) Coot bird algorithms-based tuning PI controller for optimal microgrid autonomous operation, IEEE Access 10, 6442–6458. [CrossRef] [Google Scholar]
- Huba M., et al. (2021) Making the PI and PID controller tuning inspired by Ziegler and Nichols precise and reliable, Sensors 21, 18, 6157. [CrossRef] [PubMed] [Google Scholar]
- Song M., et al. (2022) Modified harris hawks optimization algorithm with exploration factor and random walk strategy, Comput. Intell. Neurosci.. [Google Scholar]
All Tables
Comparison of metrics between proposed algorithm and previous algorithms from the literature.
Comparison of performance indices between proposed algorithm and previous algorithms from literature.
All Figures
 |
Figure 1 Management structure of HDGS with the proposed controller. |
| In the text | |
 |
Figure 2 Equivalent circuit of real model for PV panel. |
| In the text | |
 |
Figure 3 I-V and P-V characteristics of PV array. |
| In the text | |
 |
Figure 4 MPPT algorithm. |
| In the text | |
 |
Figure 5 PV system with boost converter. |
| In the text | |
 |
Figure 6 MPPT flow chart for wind generation. |
| In the text | |
 |
Figure 7 Turbine speed VSs output power. |
| In the text | |
 |
Figure 8 Wind generation system with boost converter. |
| In the text | |
 |
Figure 9 Battery storage system with DC-DC converter. |
| In the text | |
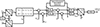 |
Figure 10 Control strategy of the DC–AC converter. |
| In the text | |
 |
Figure 11 Flowchart of the ERHHO optimization. |
| In the text | |
 |
Figure 12 Active and reactive power provided by PV-WIND and battery system. |
| In the text | |
 |
Figure 13 Active and reactive power provided by PV-WIND and battery system from 0 to 1 s. |
| In the text | |
 |
Figure 14 Active and reactive power provided by PV-WIND and battery system from 11.6 to 13 s. |
| In the text | |
 |
Figure 15 Active and reactive power provided by PV-WIND and battery system with proposed ERHHO. |
| In the text | |
 |
Figure 16 Load active and reactive power. |
| In the text | |
 |
Figure 17 Grid active and reactive power. |
| In the text | |
 |
Figure 18 PV and wind generated power. |
| In the text | |
 |
Figure 19 DC bus voltage. |
| In the text | |
 |
Figure 20 DC bus voltage comparison from 0 to 1 s. |
| In the text | |
 |
Figure 21 DC link voltage comparison from 3.9 to 6 s. |
| In the text | |
 |
Figure 22 Irradiance and wind speed change in PV and wind generation system. |
| In the text | |
 |
Figure 23 PV and wind generated power. |
| In the text | |
 |
Figure 24 Active and reactive power provided by PV-WIND and battery system with proposed ERHHO. |
| In the text | |
 |
Figure 25 Load active and reactive power. |
| In the text | |
 |
Figure 26 Grid active and reactive power. |
| In the text | |
 |
Figure 27 Battery terminal power and SOC. |
| In the text | |
 |
Figure 28 DC bus voltage. |
| In the text | |
 |
Figure 29 PV and wind generated power. |
| In the text | |
 |
Figure 30 Battery terminal power and SOC. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





![$$ \begin{array}{c}{{I}}_{{d}}={{I}}_{{ph}}-{{I}}_{{s}}\enspace \left[\mathbf{exp}\enspace \left(\frac{{q}{{V}}_{{oc}}}{{{N}}_{{s}}\enspace {KA}{{T}}_{{o}}}\right)-\mathbf{1}\right]\end{array} $$](/articles/stet/full_html/2024/01/stet20240020/stet20240020-eq28.gif)