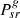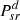| Issue |
Sci. Tech. Energ. Transition
Volume 79, 2024
|
|
|---|---|---|
| Article Number | 40 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.2516/stet/2024030 | |
| Published online | 12 July 2024 | |
Regular Article
Optimal frequency determination for wind–hydro hybrid unit using Telegrapher’s method for low-frequency transmission lines
Jadavpur University, Raja S.C. Mallick Rd, Kolkata 700032, West Bengal, India
* Corresponding author: mukulanand.anand209@gmail.com
Received:
15
May
2023
Accepted:
22
April
2024
This study addresses the optimal load flow problem for low-frequency transmission lines connected to wind farms and Pumped Storage Hydropower (PSH). The losses in the LF-HVac system and the voltage stability index are highly reliant on the operating frequency. Hence, it is essential to integrate an Optimal Load Flow (OLF) method in order to ascertain the appropriate solutions for these systems. The load flow solutions in this system involve the utilization of the Newton–Raphson method in conjunction with STATCOM. A proposed approach to simplify mathematical calculations involves the development of a two-port equivalent model for transmission lines. This model is based on solutions derived from the Telegrapher’s method. The OLF method, which has been proposed, has undergone testing with various algorithms and has been successfully implemented in the IEEE 39-BUS system. The obtained results demonstrate that the LF method, when combined with the proposed metaheuristic algorithm, achieves optimal frequency for low-frequency HVac systems while simultaneously ensuring system stability.
Key words: Optimal load flow / Telegraph method / Jaya algorithm / Low-frequency power systems
© The Author(s), published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
Notations and r : Sending and receiving bus indices
Nc: Number of STATCOM locations
NL: Number of security constraint buses
NLsr: Number of low frequency lines
Variables
Vs : Voltage magnitude at sending bus
Vr : Voltage magnitude at receiving bus
Zo : Characteristics Impedance
 :
Reactive power of power generation bus
:
Reactive power of power generation bus
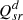 :
Reactive power of power delivery bus
:
Reactive power of power delivery bus
Pvc, Qvc : Real and reactive power of STATCOM VSC
Psr, Qsr : Real and reactive power injected
δsr : Angle of bus by which STATCOM is connected
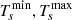 :
Transformer maximum and minimum tap setting
:
Transformer maximum and minimum tap setting
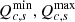 :
STATCOM max. and min. reactive power
:
STATCOM max. and min. reactive power
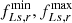 :
Minimum and maximum value of operating frequency of LF-HVac subsystem fL,sr
:
Minimum and maximum value of operating frequency of LF-HVac subsystem fL,sr
ΔAe, ΔVmn : Change in active DC power value and change in voltage of VSC converter of STATCOM
Abbreviations
LF-HVac: Low Frequency High Voltage Alternating current
STATCOM: Static Synchronous Compensator
1 Introduction
Optimal Load Flow (OLF) is inherently applied for mono-frequency systems, either 50 Hz or 60 Hz from the beginning. The change in frequency has resulted in a divergence between the aforementioned studies that prioritize voltage and the current study. Multiple converters have been developed to address frequency variations in power systems resulting from advancements in technology. The introduction of HVac brought about significant changes in the transmission of power, involving various constraints and parameters. This marked a change from the previous utilization of HVdc for power transmission. This solution facilitates the management of a multi-frequency system by considering frequency as a key parameter for achieving optimal performance. The successful implementation of the frequency-dependent OLF necessitates the fulfillment of three specific requirements. The requirement for a system that considers frequency arises from the fact that various renewable energy sources, such as wind farms, Pumped Storage Hydro (PSH), and gas turbines, produce power at different frequencies. This model incorporates frequency into existing power system models, wherein the frequency varies based on dependent parameters. Moreover, the incorporation of frequency into renewable interconnected systems can lead to fluctuations in additional parameters, including voltage stability and losses. These factors need to be carefully monitored in order to analyze the implications of frequency alterations within the system. In this study, our focus was on maintaining voltage stability and minimizing losses in the presence of frequency changes. Thirdly, the OLF (Optimal Load Flow) itself involves complex computations due to the presence of constraints, non-constraints, and parameters. In this study, the matrix formulation can be reduced by employing a reduction method, such as Telegrapher’s method, which takes into account the frequency-dependent OLF [1–11].
The utilization of power transmission at frequencies below 50 Hz or 60 Hz offers multiple benefits compared to power transmission at a fundamental frequency. The power flow solution and the system are both affected by the frequency, which is dependent on various parameters of the lines. Low frequency is commonly utilized for the analysis of transient and steady stability concerns. Therefore, it is necessary to incorporate low frequency in load flow analysis in order to accurately assess the depth calculations within the system [12–16]. Low frequency is widely utilized in various industrial applications, particularly in the development of new converters and railway systems. Recent studies have highlighted the significance of determining the optimal frequency for load flow in low-frequency transmission systems [17–19].
Nguyen and Lao in the OLF for minimizing low-frequency losses [19] introduced the predictor–corrector primal-dual interior-point method. The authors established a connection between the fundamental frequency grid and a low-frequency system in order to conduct an analysis of losses. In the thirteenth iteration, the objective function was expanded to accommodate multi-objective solutions that incorporate interfaces to low-frequency systems. BTB converters are commonly employed for interfacing multi-frequency systems. The optimal operating frequency for the BTB converter has been determined by power dispatch. Researchers have not yet determined the optimal frequency for transmission lines and converters. In order to mitigate the impact of frequency changes on system voltage, it is imperative to conduct an analysis of custom power devices. The current study does not incorporate the utilization of compensating devices to ensure voltage stability.
The frequency-dependent Optimal Power Flow (OLF) was calculated in this study by incorporating a multi-objective function. This function aimed to minimize losses and ensure voltage stability across the entire system. The utilization of STATCOM in power systems has proven effective in enhancing voltage stability and mitigating voltage fluctuations [17, 20–24].
The optimal load flow analysis is a method used to determine the operating state of a power system at the optimal point [25]. The control variables are responsible for generating voltages at precise angles and power levels. The control variables are solely dependent on the line parameters. In the past, there was no existing method that took into consideration the possibility of the frequency being dependent on line parameters. The individual in question is Roy MC. The lumped circuit model is commonly used to represent frequency-dependent line parameters. This model allows for the relationship between the variables and constraints of the load flow to be expressed as a function of frequency [26]. The components were constructed using the Telegrapher’s method. However, the current approach does not prioritize optimal load flow solutions that consider constraints and multi-objective functions.
The implementation of two-port network modeling of Telegrapher’s solution was conducted in this study, with the aim of incorporating frequency into the proposed model. The Telegrapher’s method solutions were utilized in the modeling of the objective functions for the optimal load flow solution.
The OLF, or optimal load flow, is classified as a mixed-integer non-concurring problem in conventional multi-frequency systems operating at 50/60 Hz. It involves nonlinear programming techniques. Various methodologies have been employed by researchers in order to address the OLF (Optimal Load Flow) predicament. These methodologies encompass linearization techniques as well as nonlinear programming methods. Nonlinear programming is a reliable and accurate approach for solving the OLF problem, in contrast to the limited accuracy and reliability of linearization. In a previous study [27], the authors demonstrated that the conventional Levenberg approach of Marquardt’s method may encounter convergence difficulties. Metaheuristic search methods are known for their robustness and flexibility, making them a valuable tool in tackling a wide range of complex problems. The primary objective of both metaheuristic and heuristic algorithms is to generate improved outcomes within a specified timeframe.
In 2016, a population-based approach known as the JAYA algorithm was introduced [28]. One advantage of JAYA is its ability to provide global or nearly global solutions to the optimization problem without the need for any parameter adjustments. As per JAYA, it is recommended that each individual in the population make efforts to enhance their own abilities by emulating the exemplary members and refraining from following the unproductive ones [28]. The JAYA algorithm possesses notable characteristics, such as its user-friendly interface and efficient convergence capabilities. The JAYA algorithm, like other heuristic algorithms, exhibits susceptibility to computational complexity and the potential to get stuck in local optima [29]. Researchers have proposed different versions of the original JAYA algorithm, such as the modified JAYA, in order to mitigate these drawbacks. In this study, we have employed a modified Jaya algorithm to tackle these concerns. Our approach involves the utilization of a frequency-dependent objective function. The MJAYA algorithm is designed to address the OLF problem by minimizing losses while simultaneously ensuring the preservation of both the voltage stability index and the voltage deviation index [30–34].
The remainder of this paper is organized as follows: Section 1 describes the literature related to LF-HVac, OLF, and Telegrapher’s equation. Section 2 describes the system methodology. Section 3 discusses the various aspects of the proposed formulation. In Section 4, we discuss the solution approach. Finally, different case studies are discussed in Section 5, and conclusions are presented in Section 6.
2. Formulation
In this section, the frequency dependence of the line parameters proposed using Telegrapher’s equation in multi-objective formation is explained. STATCOM was introduced for voltage stability in transmission systems. In addition, a two-port network with an impedance analysis is described in this section.
2.1 Frequency-dependent model and STATCOM
The linear combination of frequency as a function of the parameters of multi-frequency system is expressed in this section. f1, f2,…. fs are the different frequencies of the different systems m1, m2,…ms.
Let us consider m1 as a subsystem with one frequency f1 and so on, as shown in Figure 1. Then, the power combination of the multi-frequency system with a fundamental frequency system can be represented by (1)
f can be less than or equal to 60 Hz.
(1)
f can be less than or equal to 60 Hz.
 |
Figure 1 Basic model of LF-HVac. |
In Figure 1, a back-to-back converter was used as a frequency converter for each renewable system. Therefore, to integrate the multi-frequency system, the fundamental ratio coefficient k was introduced to correlate the two systems. The load flow line parameters were modified to make them frequency-dependent. K can be represented by equation (2), where fr is the fundamental frequency, and f1 and f2 represent the lower frequencies of the power system. (2)
(2)
Therefore, to modeling the branch and line parameters, the line resistance R, inductance L, capacitance C, and shunt conductance G in p. u. are taken as it is but frequency-dependent X as series reactance and B as susceptance of transmission lines are modified in terms of k as follows: (3)
(3)
 (4)
(4)
where s and r denote the sending and receiving buses, respectively. As we know, three-phase winding transformers are independent of frequency, so they depend only on tap values. In the proposed model, we generalized the STATCOM model to a real tap-changing transformer, where the tap ratio ‘T’ of the transformer changes with a change in the voltage of the respective bus. (5)
(5)
A simplified model of the STATCOM can be obtained using equation (5). Where Vsr,vc is the phase voltage of Voltage Source Converter (VSC) and 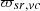 is the phase angle, T
′ represents the variable tap of the transformer and Edc shows the voltage across the DC source of the converter).
is the phase angle, T
′ represents the variable tap of the transformer and Edc shows the voltage across the DC source of the converter).
For a three-phase winding transformer, the tap magnitude can be expressed as [20]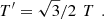 (6)
(6)
In the above equation, the tap ratio will be a continuously changing variable, and T ′ will be rounded off to an integer with the nearest value.
2.2 Two port equivalent model of transmission system based on Telegrapher’s method
A simplified formulation between the two buses is shown in Figure 2 where Rdx, Ldx, Gdx, and Cdx are considered as transmission lines of small lengths.
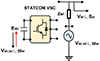 |
Figure 2 Simplified model of transmission line. |
The frequency G, L, and C are dependent quantities that change with transmission. Therefore, the transmission losses also depend on the G value.
Admittance of line can be expressed as (7)
(7)
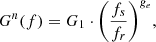 (8)where shunt conductance G is dependent on frequency and ge is Terman’s statement constant, which is considered to be 1 for a uniform transmission line [7].
(8)where shunt conductance G is dependent on frequency and ge is Terman’s statement constant, which is considered to be 1 for a uniform transmission line [7].
Voltage and current solution in case of sinusoidal steady state can be expressed as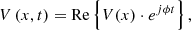 (9)
(9)
 (10)
(10)
where φ denotes angular frequency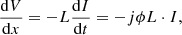 (11)
(11)
 (12)
(12)
Differentiating equations (11) and (12),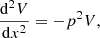 (13)
(13)
 (14)
(14)
where 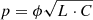 is a frequency-dependent equation in the solution of the Telegrapher’s method. So,
is a frequency-dependent equation in the solution of the Telegrapher’s method. So, (15)
(15)
For a lossy transmission line of fixed length, the ports are excited by voltage sources at the sending end with an angular frequency φ.
Unbalanced single-conductor transmission lines were assumed in the proposed system, as shown in Figure 3.
 |
Figure 3 Two port model of unbalanced transmission line. |
Because x is constant for our proposed model, the voltage and current of the two-port network of the solution of the Telegrapher’s equations as an ABCD type can be expressed as![$$ \left[\begin{array}{c}{V}_s\\ {I}_s\end{array}\right]=\left[\begin{array}{cc}\mathrm{cosh}\left({\gamma x}\right)& \mathrm{sinh}\left({\gamma x}\right)\cdot {Z}_o\\ \frac{\mathrm{sinh}\left({\gamma x}\right)}{{Z}_o\enspace }& \mathrm{cosh}\left({\gamma x}\right)\end{array}\right]\enspace \left[\begin{array}{c}{V}_r\\ {I}_r\end{array}\right], $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq35.gif) (16)where A = cosh(γx), B=sinh(γx)·Zo,
(16)where A = cosh(γx), B=sinh(γx)·Zo,  and D = cosh(γx).
and D = cosh(γx).
Equations (9)–(15) show that the solutions are frequency-dependent and are considered for optimal load flow solutions. From equation (16), the receiving and sending end voltages can be derived and expressed as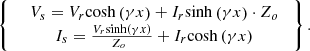 (17)
(17)
From (17)
 (18)
(18)
3 Proposed formulation
3.1 Objective functions
3.1.1 Loss minimization
3.1.1.1 Losses in LF-HVac system
Losses can be expressed as![$$ F=\sum_{s=1}^N\sum_{\begin{array}{c}r=1\\ s\ne r\end{array}}^N\frac{{G}_{{sr}}^n}{2}\left[{\left|{V}_s^n\right|}^2+{\left|{V}_r^n\right|}^2-2\left|{V}_s^n\right|\left|{V}_r^n\right|\mathrm{cos}\left({\delta }_s-{\delta }_r\right)\right]. $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq41.gif) (19)
(19)
For a perfectly grounded system, Zo = 0 Therefore, the transmission losses become localized and cosh becomes 1 and sinh ~ 0; hence, (18) can be reduced to
Therefore, the transmission losses become localized and cosh becomes 1 and sinh ~ 0; hence, (18) can be reduced to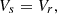 (20)
(20)
Substituting (20) into (19), losses are modified to locally estimated transmission losses by one of the ends [11]. This loss also depends on the angle difference between the two ends. Hence, the new losses that can be designated as node losses Fn are as follows:![$$ {F}_n=\sum_{s=1}^N\sum_{\begin{array}{c}r=1\\ s\ne r\end{array}}^N{G}_{{sr}}^n\left[{\left|{V}_r^n\right|}^2(1-\mathrm{cos}\left({\delta }_s-{\delta }_r\right))\right]. $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq45.gif) (21)
(21)
The plot of the node loss Fn as a function of Vr in (21) is shown in Figure 4.
 |
Figure 4 New loss function F1 and Fc plot. |
3.1.1.2 Losses in converters
The VSCs loss Fc in the low-frequency system, as shown in Figure 5 is calculated using the generalized formula of converter loss, which is dependent on the injected current shown in (22) [8].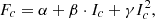 (22)where α, β, and γ are the loss coefficients of the VSC connected to LF lines. The injected current Ic can be expressed as
(22)where α, β, and γ are the loss coefficients of the VSC connected to LF lines. The injected current Ic can be expressed as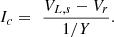 (23)
(23)
 |
Figure 5 Simplified model of low frequency converters connected to AC grid. |
From (23), Ic is also dependent on Y, which in turn is dependent on the frequency, as shown in (7) and (8). Thus, the overall losses comprise converter losses and node losses of the LF-HVac system, which can be expressed as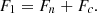 (24)
(24)
3.1.2 Voltage stability index
For a perfectly grounded system, as per (20), (25) can be expressed as (26)
(26)
3.1.3 Voltage deviation Index
The Voltage Deviation Index (VDI) of the network voltage profile can be expressed as: (27)where SPQ is load bus, Vref is taken as 1 p.u.
(27)where SPQ is load bus, Vref is taken as 1 p.u.
3.1.4 Quadratic weighted sum objective function
The multi-objective function was reduced to a single objective function by allocating a weight to each objective function and then optimizing the weighted sum quadratic function. However, there are no restrictions on choosing a form for this problem. This method provides good solutions for the Pareto front, as shown in Figure 6. Thus, the objective function can be expressed as (28)where the Wi weighing coefficients can be determined by the linear weighted sum method, which can be determined by equation (30).
(28)where the Wi weighing coefficients can be determined by the linear weighted sum method, which can be determined by equation (30).
 |
Figure 6 Pareto front of objective functions. |
Because the objective is to minimize the inconsistent objective function Fq to implement without hampering generality, it can be regarded as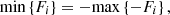 (29)where Fi is a quadratic function in the proposed case, Wi € R and is the weight of the ith objective function.
(29)where Fi is a quadratic function in the proposed case, Wi € R and is the weight of the ith objective function. (30)
(30)
From Figure 7. The best solution using a quadratic weighted sum can be observed with linear weighted coefficients where n is taken as 3.
 |
Figure 7 Quadratic weighted objective function. |
3.2 Constraints
3.2.1 Equality constraints
The mathematics of power systems are connected to the OPF equality criteria. Moreover, inequality limitations reflect the restrictions placed on the physical components of power systems, as well as the restrictions put in to ensure network security. The equality constraints for the power flow equations are given by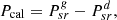 (31)
(31)
 (32)
(32)
3.2.2 Inequality constraints
Inequality constraints for different units of the system are (33)
(33)
 (34)
(34)
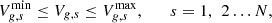 (35)
(35)
 (36)
(36)
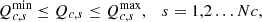 (37)
(37)
 (38)
(38)
 (39)
(39)
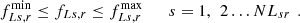 (40)
(40)
3.3 STATCOM power constraints
The power constraints of the STATCOM equivalent model of STATCOM as shown in Figure 8 can be represented by (41)
(41)
 (42)
(42)
![$$ \begin{array}{c}{P}_{{vc},{sr}}={V}_{{sr}}^2{G}_{{vc},{sr}}+{V}_{{sr}}{V}_{{sr},{vc}}\\ \left(\left[\begin{array}{c}{G}_{{sr},{vc}}\mathrm{cos}\left({\varpi }_{{sr},{vc}},{\delta }_{{sr}}-{\delta }_{{sr}},{\varpi }_{{sr},{vc}}\right)+\\ {B}_{{sr},{vc}}\enspace \mathrm{sin}\left({\varpi }_{{sr},{vc}},{\delta }_{{sr}}-{\delta }_{{sr}},{\varpi }_{{sr},{vc}}\right)\end{array}\right]\right),\enspace \\ \enspace \end{array} $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq84.gif) (43)
(43)
![$$ \begin{array}{c}{Q}_{{vc},{sr}}=-{V}_{{mn}}^2{G}_{{vc},{sr}}+{V}_{{sr}}{V}_{{sr},{vc}}\\ \left(\left[\begin{array}{c}{G}_{{sr},{vc}}\mathrm{cos}\left({\varpi }_{{sr},{vc}},{\delta }_{{sr}}-{\delta }_{{sr}},{\varpi }_{{sr},{vc}}\right)-\\ {B}_{{sr},{vc}}\mathrm{sin}\left({\varpi }_{{sr},{vc}},{\delta }_{{sr}}-{\delta }_{{sr}},{\varpi }_{{sr},{vc}}\right)\end{array}\right]\right)\enspace.\enspace \\ \enspace \end{array} $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq85.gif) (44)
(44)
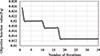 |
Figure 8 Equivalent diagram of STATCOM. |
4 Solution method based on MJAYA
The Jaya Algorithm is a population-based algorithm inspired by the social behavior of individuals in a society, particularly in terms of cooperation and mutual improvement and is used to solve OLF. This algorithm was developed by Rao in 2009. Suppose dth is a member of the tth variable; then, the position is updated by![$$ {X}_{d,t}={X}_t^{\mathrm{min}}+\mathrm{rand}\left(\cdot \right)\left[{X}_t^{\mathrm{max}}-{X}_t^{\mathrm{min}}\right], $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq86.gif) (45)
(45)
![$$ {X}_{t,d,s}^{\mathrm{new}}={X}_{t,d,s}+{r}_{1,t,m}\left[\left({X}_{t,{best},s}\right)-\left(\left|{X}_{t,d,s}\right|\right)\right]-{r}_{2,t,s}\left[\left({X}_{t,\mathrm{worst},s}\right)-\left(\left|{X}_{t,d,s}\right|\right)\right], $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq87.gif) (46)
(46)
where  are the new solutions of the tth variable and r1,t,s and r2,t,s are randomly generated values between 1 and 0 of the tth variable. Xt,best,s and Xt,worst,s are the best and worst values, respectively, of the tth variable.
are the new solutions of the tth variable and r1,t,s and r2,t,s are randomly generated values between 1 and 0 of the tth variable. Xt,best,s and Xt,worst,s are the best and worst values, respectively, of the tth variable.
Therefore, to eliminate the disadvantages of the Jaya algorithm, the updating solution equation can be modified as![$$ {X}_{t,d,s}^{\mathrm{new}}={X}_t^{d,s}+{r}_{1,t,s}\left[{X}_{t,\mathrm{worst},s}-\left|{X}_{t,d,s}\right|\right]-{L\times r}_{2,t,s}\left[{{X}_{t,d,s}}^2-{{X}_{t,\mathrm{best},s}}^2\right], $$](/articles/stet/full_html/2024/01/stet20230101/stet20230101-eq89.gif) (47)where L is the coefficient determined in every iteration, and L = 1 if rand > 0.5; otherwise, it is −1. The flowchart demonstrates the proposed algorithm in more detail, as shown in Figure 9.
(47)where L is the coefficient determined in every iteration, and L = 1 if rand > 0.5; otherwise, it is −1. The flowchart demonstrates the proposed algorithm in more detail, as shown in Figure 9.
 |
Figure 9 MJAYA algorithm for optimal frequency selection. |
Each optimization algorithm had unique parameters. In PSO, c1 and c2 were set to 1.5, the population size was set to 310, and the number of iterations was set to 400. The default weights of w1 and w2 are taken as 0.5 and 0.9, respectively. For the BRO algorithm, the number of iterations and population size remained the same, and the weight factor W1 varies from [0–1]. Because Jaya is a gradient-free algorithm, it requires no parameters other than random values. Figure 10 depicts the convergence characteristics of the various algorithms with and with frequency constraints on the transmission lines. According to figure, the proposed MJAYA OLF provided the best results for all LF-HVac lines. Twenty separate runs were performed for each algorithm to gauge how frequently the optimal or nearly optimal solution was reached while preserving the same stopping conditions, thereby demonstrating the resilience and consistency of the proposed method (a maximum of 400 iterations).
 |
Figure 10 Convergence comparison with different optimization algorithms with LF-HVac line. |
5 Case studies
In this section, the benefits of the proposed formulation in Section 3 and solution method in Section 4 are presented. The proposed OLF algorithm can reduce losses, increase the stability index, and maintain voltage stability in LF-HVAC transmission lines. The proposed methodology not only reduces the matrix calculation significantly but also reduces the parameters in the OLF. The two-port network solution of Telegrapher’s method reduces the loss equation to a single-parameter variation.
The proposed OLF was tuned and performed best with a 310 person population and 400 iterations, as shown in Table 1.
Study of optimal parameters.
5.1 System design
The test system comprised 10 generating units connected by 39 transmission network branches, as shown in Figure 11. The following topology diagram represents the IEEE 39-bus system, where bus 39 is a slack bus: With the possible exception of the slack bus, the buses (30–38) connected to each generator had voltage levels of 20–38 kV, 11–38 kV, and 500 kV for all other buses. In this study, a MATLAB-based simulation tool was used to perform OLF on a two-port system. A metaheuristic algorithm was presented with a quadratic-weighted single-objective function. This method reduces the number of calculations and matrix formations.
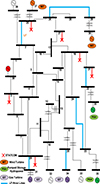 |
Figure 11 Line diagram of modified IEEE 39 bus test system. |
To solve the complexity of voltage and frequency changes in low-frequency HVAC systems, the ratio coefficient k is introduced in Section 2, where Vbase and fbase are taken as 500 kV and 60 Hz, respectively. Table 2 represnts the voltage levels of RES. For any transmission line, the variation in reactance and resistance is very small, that is, 0.10% and 0.20%, respectively, as shown in [15]. However, in our proposed model, low frequency affects the Xn, Yn, and Gn of the transmission lines as per the k coefficient between the s and r buses. With each iteration of the optimal load flow, the values of conductance Gn and susceptance Bn are updated with the change in frequency of the system, as per [15].
Voltage levels of RES.
Subsequently, the Modified JAYA with STATCOM inclusion is updated with new variables, constraints, and parameters while achieving the optimal load flow. Using two-port network analysis and Telegrapher’s method, the objective functions are modified to form new functions. Frequency consideration in a simplified two-port network provides a better solution than in a conventional one.
5.2 Assessment of voltage stability
The STATCOMs were placed at six buses (5, 16, 21, 25, 27, and 29) in the proposed system to maintain voltage stability. Initially, the OLF was run without STATCOM on a 39 IEEE bus system and was estimated in terms of a modified objective function (Fq). To visualize the impact of the frequency change, two separate runs of the OPF were formulated and compared. In the first run, the optimal load flow with the function Fq and frequency change parameters were included. STATCOM includes the same parameters, functions, and Z for the next run.
Figure 12 shows that the buses with the STATCOM have a significant improvement in voltage stability over the first case. The voltage level changes by up to 0.4% on bus 5 with LF-HVac lines and 0.1%–0.4% on other buses, demonstrating that the bus with STATCOM and LF-HVac lines provides better voltage stability than buses without LF-HVac lines. This indicates that the placement of the STATCOM is favorable for the proposed system, which provides optimistic results.
 |
Figure 12 Voltage profile for LF-HVAC lines with STATCOM. |
5.3 Numerical analysis of proposed system for fixed frequency range
The purpose of the presented results was to demonstrate the agility of the proposed algorithm with a defined solver. To visualize this, the system was tested with the proposed OLF, which consists of six LF-HVAC transmission lines, that is, (31–29), (34–20), (23–24), (21–22), (2–25), and (26–29) connected to wind farms, pumped storage hydropower, and gas turbines. All transmission lines have BTB converters with a working range of 0.9–1.0 p.u. with discrete step sizes of 0.01. Table 2 shows that the generator buses maintained the voltage limits with a maximum change of 0.089% in low-frequency transmission lines. MJAYA also outperforms the others in resolving the OLF issue while achieving the optimal frequency of each low-frequency line for a predefined range [15–20 Hz], as shown in Table 3.
Results with proposed algorithm and low frequency lines.
5.4 Loss analysis for different frequency range
In this scenario, losses were incurred as a function of the frequency range. The losses were calculated with and without the optimal load flow. Figure 13 without OLF, the proposed system’s losses remain constant at 0.4491 MW, whereas after OLF, the losses decrease in a different frequency range. In the 31–40 Hz range, the losses are minimal with OLF, so an optimal frequency range can be depicted. From Figure 14 loss was found for the proposed system, and a frequency range of 31–40 Hz was depicted as the optimal range.
 |
Figure 13 Losses with OLF and without OLF. |
 |
Figure 14 Convergence characteristics of losses with OLF. |
5.5 Loss analysis for different frequency range
In this scenario, losses were incurred as a function of the frequency range. The losses were calculated with and without the optimal load flow. Figure 13 without OLF, the proposed system’s losses remain constant at 0.4491 MW, whereas after OLF, the losses decrease in a different frequency range. In the 31–40 Hz range, the losses are minimal with OLF, so an optimal frequency range can be depicted. From, Figure 14 Loss was found for the proposed system, and a frequency range of 31–40 Hz was depicted as the optimal range.
5.6 Statistical analysis for each low frequency lines
The optimal frequency with the proposed algorithm and solver is shown in Figure 15 shows the frequency deviation of low-frequency transmission lines (WT, PSH, and GT), which can reach a maximum of ±5 Hz. Also Figure 16 shows the standard error of the frequency for each low-frequency line.
 |
Figure 15 Frequency deviation of low-frequency lines. |
 |
Figure 16 Standard deviation of low-frequency lines. |
6 Conclusion
The optimal frequency selection for the LF-HVac transmission system was studied in this work. We investigated OLF by utilizing a reduced quadratic weighted objective function. A two-port equivalent transmission system was implemented to modify the objective function and reduce the variables based on Telegrapher’s method. We proposed the MJAYA algorithm with optimal coefficient selectivity to validate the correctness of our proposed algorithm. Conducting load flow analysis using STATCOM effectively enhanced the voltage stability under various frequency constraints. The results are compared with those of alternative optimization methods, which show that the application of Telegrapher’s equation consistently outperforms the existing approaches. The proposed quadratic weighted objective function provided better results for the stability index and loss minimization function with frequency attributes. We determined the optimal frequency for each low-frequency line. In addition, the proposed formulation for the optimal frequency selection for transmission lines can incorporate new custom power devices.
References
- Sehloff D., Roald L. (2020) Steady state modeling for variable frequency ac power flow, in North American Power Symposium (NAPS), IEEE. ArXiv preprint available at https://arxiv.org/abs/2101.11113. [Google Scholar]
- Soriano Rangel A., Mancilla-David F. (2018) Hexverter–based optimal low frequency AC transmission system, in North American Power Symposium, IEEE. [Google Scholar]
- Nguyen Q., Ngo T., Santoso S. (2016) Power flow solution for multifrequency ac power systems, in 2016 IEEE/PES Transmission and Distribution Conference and Exposition (TD), IEEE. [Google Scholar]
- Sehloff D., Roald L.A. (2022) Low frequency AC transmission upgrades with optimal frequency selection, IEEE Trans. Power Syst. 37, 2, 1437–1448. https://doi.org/10.1109/TPWRS.2021.3107193. [CrossRef] [Google Scholar]
- Warid W., Hizam H., Mariun N., Abdul-Wahab N. (2016) Optimal power flow using the Jaya algorithm, Energies 9, 9, 678. [CrossRef] [Google Scholar]
- Pandey H.M. (2016) Jaya a novel optimization algorithm: What, how and why?, in 2016 6th International Conference – Cloud System and Big Data Engineering (Confluence), pp. 728–730. [CrossRef] [Google Scholar]
- Angeles C., Mercader E.J., Tan G.E., Pacis M.C., Bersano R.F. (2017) Fault evaluation and performance of an IEEE bus 30 power distribution network with distributed generation (DG), in 2017 HNICEM Proceedings, IEEE. [Google Scholar]
- Acha E., Fuerte-Esquivel C.R., Ambriz-Perez H., Angeles-Camacho C. (2004) FACTS: modelling and simulation in power networks, John Wiley & Sons. [CrossRef] [Google Scholar]
- Chen W.Y. (2004) Home networking basics, Prentice Hall, p. 26. ISBN 0-13-016511-5. [Google Scholar]
- Daelemans G. (2008) VSC HVDC in meshed networks, Master’s thesis, Katholieke Universiteit Leuven, Leuven, Belgium. [Google Scholar]
- Cordero R. (1996) Estimation of Transmission Losses in a Changing Electric Power Industry, Massachusetts Institute of Technology. [Google Scholar]
- Nguyen Q., Todeschini S., Santoso S. (2019) Power flow in a multifrequency hvac and hvdc system: Formulation, solution, and validation, IEEE Trans. Power Syst. 36, 4, 2487–2497. [CrossRef] [Google Scholar]
- Nguyen Q., Santoso S. (2021) Optimal planning and operation of multi-frequency HVac transmission systems, IEEE Trans. Power Syst. 36, 1, 689–398. https://doi.org/10.1109/TPWRS.2020.3037967. [CrossRef] [MathSciNet] [Google Scholar]
- Sayed A.R., Wang C., Anis H., Bi T. (2022) Feasibility constrained online calculation for real-time optimal power flow: a convex constrained deep reinforcement learning approach, IEEE Trans. Power Syst. https://doi.org/10.1109/TPWRS.2022.3220799. [Google Scholar]
- Ahrabi R.R., Li Y.M., Nejabatkhah F. (2021) Hybrid AC/DC network with parallel LCC-VSC interlinking converters, IEEE Trans. Power Syst. 36, 1, 722–731. https://doi.org/10.1109/TPWRS.2020.3020235. [CrossRef] [Google Scholar]
- Van Cutsem T., Glavic M., Rosehart W., Andrade dos Santos J., Cañizares C., Kanatas M., Lima L., Milano F., Papangelis L., Andrade Ramos R., Tamimi B. (2015) Test systems for voltage stability analysis and security assessment, Technical Report, IEEE. [Google Scholar]
- Li C., Burgos R., Wen B., Tang Y., Boroyevich D. (2020) Stability analysis of power systems with multiple STATCOMs in close proximity, IEEE Trans. Power Electron. 35, 3, 2268–2283. https://doi.org/10.1109/TPEL.2019.2931891. [CrossRef] [Google Scholar]
- Hraiz M.D., García J.A.M., Jiménez Castañeda R., Muhsen H. (2020) Optimal PV size and location to reduce active power losses while achieving very high penetration level with improvement in voltage profile using modified jaya algorithm, IEEE J. Photovolt. 10, 4, 1166–1174. https://doi.org/10.1109/JPHOTOV.2020.2995580. [CrossRef] [Google Scholar]
- Arshad M.H., Abido M.A., Salem A., Elsayed A.H. (2019) Weighting factors optimization of model predictive torque control of induction motor using NSGA-II with TOPSIS decision making, IEEE Access 7, 177595–177606. https://doi.org/10.1109/ACCESS.2019.2958415. [CrossRef] [Google Scholar]
- Kazemtabrizi B., Acha E. (2014) An advanced STATCOM model for optimal power flows using Newton’s method, IEEE Trans. Power Syst. 29, 2, 514–525. [CrossRef] [Google Scholar]
- Santos A. Jr., Costa G.R.M.d. (1995) Optimal power flow solutions by Newton’s method applied to an augmented Lagrangian function, IEE Proc. Gen. Transm. Distrib. 142, 33–36. [CrossRef] [Google Scholar]
- Wafaa M.B., Dessaint L.-A. (2017) Multi-objective stochastic optimal power flow considering voltage stability and demand response with significant wind penetration, IET Gener. Transmiss. Distrib. 11, 14, 3499–3509. [CrossRef] [Google Scholar]
- Platbrood L., Capitanescu F., Merckx C., Crisciu H., Wehenkel L. (2014) Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems, Int. J. Ind. Eng. Comput. 29, 3, 19–34. [Google Scholar]
- Venkata Rao R. (2016) Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems, Int. J. Ind. Eng. Comput. 19–34. [Google Scholar]
- Nguyen N., Almasabi S., Bera A., Mitra J. (2018) Optimal power flow considering frequency security constraint, in Proc. IEEE PES/IAS Power Africa Conf., IEEE, pp. 1–6. [Google Scholar]
- Sun D.I., Ashley B., Brewer B., Hughes A., Tinney W.F. (1984) Optimal power flow by Newton approach, IEEE Trans. Power App. Syst. PAS-103, 10, 2864–2880. [CrossRef] [Google Scholar]
- Anand M., Goswami S.K., Chatterjee D. (2022) Multi-frequency control with fuzzy 2DOFPI in HVBTB converter of LF-HVAC system, Int. J. Emerg. Electr. Power Syst. 24, 6, 717–728. https://doi.org/10.1515/ijeeps-2022-0133. [Google Scholar]
- Acha E., Fuerte-Esquivel C.R., Ambriz-Perez H., Angeles-Camacho C. (2005) FACTS modeling and simulation in power networks, Wiley, New York, NY, USA. [Google Scholar]
- Tien D.V., Gono R., Leonowicz Z., Krejci P. (2019) Load flow analysis in power system network incorporating STATCOM: A comparison of the direct and indirect algorithm of the Newton-Raphson method, Adv. Electr. Electron. Eng. 17, 1, 13–23. [Google Scholar]
- Tang W., Wu B., Zhang L., Zhang X., Li J., Wang L. (2021) Multi-objective optimal dispatch for integrated energy systems based on a device value tag, CSEE J. Power Energy Syst. 7, 3, 632–643. https://doi.org/10.17775/CSEEJPES.2019.02650. [Google Scholar]
- Jha R.R., Inaolaji A., Biswas B.D., Suresh A., Dubey A., Paudyal S., Kamalasadan S., (2022) Distribution grid optimal power flow (d-opf): Modeling, analysis, and benchmarking, IEEE Trans. Power Syst. 38, 4, 3654–3668. [Google Scholar]
- Ngo T., Lwin M., Santoso S. (2016) Steady-state analysis and performance of low frequency ac transmission lines, IEEE Trans. Power Syst. 31, 5, 3873–3880. [CrossRef] [Google Scholar]
- Acha E., Kazemtabrizi B. (2013) A new STATCOM model for power flows using the Newton-Raphson method, IEEE Trans. Power Syst. 28, 3, 2455–2465. [CrossRef] [Google Scholar]
- Mohanty R., Chatterjee D., Suman S., Anand M. (2023) A reduced switch count multilevel inverter for PV standalone system using modified JAYA algorithm, Int. J. Electron. 111, 2, 360–378. [Google Scholar]
All Tables
All Figures
 |
Figure 1 Basic model of LF-HVac. |
| In the text | |
 |
Figure 2 Simplified model of transmission line. |
| In the text | |
 |
Figure 3 Two port model of unbalanced transmission line. |
| In the text | |
 |
Figure 4 New loss function F1 and Fc plot. |
| In the text | |
 |
Figure 5 Simplified model of low frequency converters connected to AC grid. |
| In the text | |
 |
Figure 6 Pareto front of objective functions. |
| In the text | |
 |
Figure 7 Quadratic weighted objective function. |
| In the text | |
 |
Figure 8 Equivalent diagram of STATCOM. |
| In the text | |
 |
Figure 9 MJAYA algorithm for optimal frequency selection. |
| In the text | |
 |
Figure 10 Convergence comparison with different optimization algorithms with LF-HVac line. |
| In the text | |
 |
Figure 11 Line diagram of modified IEEE 39 bus test system. |
| In the text | |
 |
Figure 12 Voltage profile for LF-HVAC lines with STATCOM. |
| In the text | |
 |
Figure 13 Losses with OLF and without OLF. |
| In the text | |
 |
Figure 14 Convergence characteristics of losses with OLF. |
| In the text | |
 |
Figure 15 Frequency deviation of low-frequency lines. |
| In the text | |
 |
Figure 16 Standard deviation of low-frequency lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.