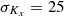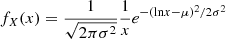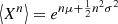| Issue |
Sci. Tech. Energ. Transition
Volume 78, 2023
Characterization and Modeling of the Subsurface in the Context of Ecological Transition
|
|
|---|---|---|
| Article Number | 42 | |
| Number of page(s) | 40 | |
| DOI | https://doi.org/10.2516/stet/2023036 | |
| Published online | 22 December 2023 | |
Regular Article
Foam placement for soil remediation: scaling foam flow models in heterogeneous porous media for a better improvement of sweep efficiency
1
IFP Energies nouvelles, Earth Sciences and Environmental Technologies Division, 1 et 4 avenue de Bois Préau, 92852 Rueil-Malmaison Cedex, France
2
IFP Energies nouvelles, Digital Sciences and Technologies Division, 1 et 4 avenue de Bois Préau, 92852 Rueil-Malmaison Cedex, France
* Corresponding author: frederic.douarche@ifpen.fr
Received:
2
September
2022
Accepted:
10
November
2023
If injected with a large gas fraction, foam reduces mobility more in high-permeability layers and diverts flow to low-permeability layers. Here is a qualitative statement that has been claimed many times in many works related to environmental remediation and oil recovery. It is so true and relevant for foam flow in porous media and yet so little quantified and even less exploited in Darcy-scale numerical simulation. After briefly reviewing opportunities and challenges related to the use of foams in porous media and its Darcy-scale implicit-texture and population-balance modelling, we make a detour out of the strict framework of mathematical models by revisiting with a fresh eye the physics of foams on the large scale of heterogeneous natural porous media in terms of scaling laws. Specifically, it has been recently shown experimentally and theoretically that foam mobility reduction scales approximately as the square root of rock permeability within the framework of Darcy-type implicit-texture foam flow models [Douarche et al. (2020) Scaling foam flow models in heterogeneous reservoirs for a better improvement of sweep efficiency (Paper ThB04), in:17th European Conference of the Mathematics of Oil Recovery (ECMOR), Edinburgh, Scotland, 14–17 September; Gassara et al. (2020) Trans. Porous Media 131, 1, 193–221]. This also appears to hold for population-balance models under the local steady state assumption. This quantitative scaling law for the effect of permeability on foam properties was inferred from an analogy between foam flow in porous media and foam flow in capillary tubes and was found consistent with the modelling of available experimental data. We demonstrate by varying the permeability contrast and anisotropy of a stack of porous layers how foam regulates the flow and leads to flow diversion from high- to low-permeability layers. The threshold in permeability heterogeneity for which such a foam-driven diversion becomes effective is quantified through a sensitivity study accounting for foam injection type, permeability heterogeneity and anisotropy, heterogeneity structure, and scaling procedure. The simulations carried out clearly indicate that ignoring mobility reduction dependence on permeability in the foam process assessment of heterogeneous formations leads to an underestimation of mobility reduction benefits to improve flow conformance. The question of cores selection, as this rock-typing strategy in relation to the porous medium characterization may guide a smart and optimal design of pre-feasibility laboratory campaign for foam evaluation, and the generalization of the findings to multi-facies geological formations are also discussed. As such, the use of physical foam mobility reduction scaling law is highly recommended for foam process evaluation.
Key words: Multiphase flow / Porous media / Foam / Scaling laws / Heterogeneity / Models / Simulation / Soil remediation
Foreword: This paper includes a large Appendix A.2 which reports some selected in-situ foam flow dynamic behaviour. These figures are discussed in the main text but have been put in appendix to facilitate the reading. Its consultation remains optional, but the authors believe the reader will find there a good complement to the production data overall response of the porous medium under foam flooding.
© The Author(s), published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Understanding and predicting foam flow behaviour in heterogeneous porous media, matricial or naturally fractured, is a generic and extremely complex problem which is often encountered in geosciences applications involving the displacement of a non-aqueous phase liquid (NAPL) by water and/or gas [1–6], given that the behaviour of foams in porous media is far from being elucidated and remains a subject of active research. Whether the targeted application is soil remediation, carbon capture, utilization and storage or hydrocarbon production, foam suffers from two major fundamental limitations: surfactant adsorption on rock and the anti-foaming character of the NAPL to displace, as is the case of most pollutants and oil.
The result of these two strong constraints, if one considers foam as a NAPL frontal displacing fluid, is a fundamental contradiction that is very difficult to resolve in practice between the need to limit the amount of surfactants injected for obvious economic reasons [2, 4] and the dual penalty foam suffers from, namely not only chemicals adsorption on rock but also the anti-foaming character of the NAPL to displace that yields additional losses and requires even more chemicals to compensate for. In this regard, the use of foams for CO2 storage in aquifer does not present the anti-foaming NAPL issue but is more questionable technically unless foam improves the effective storage capacity by smoothing out viscous fingering that may develop between CO2 and brine and/or channeling due to heterogeneity through conformance control [7], provided foams are stable over the long-term.
In this context, one can only hope that new foaming formulations that are cheaper, more resistant to NAPL, less adsorbent, more stable over the long term, and more respectful of the environment will be developed. Application-wise, the story could end there, but hopefully, in addition to their large apparent viscosity which could have been very effective in frontal displacement, unfortunately impacted by the anti-foaming nature of fluids such as NAPL and oil, foams have attractive selectivity properties in porous media which may change the game and are the subject of this paper.
In the perspective of a large-scale deployment of this type of injection, the investments necessary for the implementation of such a process on geological formations of hectometric or kilometric size and the associated risks require predictive models making it possible to determine optimal injection configurations that are robust to the inherent subsurface uncertainties beforehand. One must admit it is illusory, at this geological scale under consideration, to aspire to model the physics of foams in porous media at the pore scale, even assuming it would be completely known at this scale. Indeed, if the numerical calculation allowed it one day, on the condition of a fully known physics, the problem of the time- and length-scales that can be sampled for subsurface characterization hence the set-up of the initial boundary value problem, and the resulting unavoidable uncertainties would remain. Even if we could integrate the pore-scale motion equations in a general form, it would be completely impossible to substitute in the general solution the (uncertain) initial conditions for the velocities, pressures, saturations and compositions of all the phases at reservoir scale. As an example, considering a typical pore size of about 50 μm, a porous medium of 20% porosity, 200 × 200 m extension and 50 m thickness counts very roughly about a billion pores.
It goes without saying that high performance computing and rock-solid physical laws are useless without an accurate characterization of the porous medium under consideration, which certainly does not extend to the scale of the cubic centimeter and even less of the pore over an entire geological formation. Thus, if a reasonable and convenient modelling trade-off is to build semi-empirical augmented generalized multiphase Darcy-type models to describe coarsely foam flow as we shall see in the following, a certain void remains between the pore scale and that already homogenized of the fictitious continuous medium considered at the Darcy’s scale.
Given the atrocious complexity of the problem, it is likely that no answer will be provided anytime soon regarding the upscaling of foam flow within a multiphase framework from the pore to a representative geological scale. In industrial practice, either one resorts to case-by-case evaluations that involve massive laboratory studies sampling the heterogeneity variability of the porous medium under consideration, which are necessarily extremely expensive (therefore extremely rare and most often proprietary), or goes with the wet finger hunch with very few measurements and some literature survey (win or loose strategy when the risks allow it). One of the major obstacles lies in the absolutely phenomenal amount of work (and costs) that it represents to engage in feasibility studies without having the certainty of choosing foams as a displacement fluid at the end.
This work transposes a knowledge coming from reservoir engineering to environmental engineering, with however differences between those two application fields, mostly (i) in term of permeability that is usually much higher for aquifers, and (ii) in term of air that can be present in the transition zone of near-subsurface undersaturated soils. The thermodynamic conditions considered are representative of deep subsurface porous media, not of shallow aquifers, but have little impact on the results of this work that is mainly phenomenological in nature. This work represents a first conceptual attempt and does not claim to cover all possible cases.
We show the contribution of a sensible physical coarse-grain approach based on scaling laws that is resolutely pragmatic and which has the advantage of being neither simplistic nor involving massive workflows which are known to be difficult to implement in practice. From a workflow perspective, as we shall see, the authors are not suggesting any additional complexity but rather a smart and optimal guidance for foam evaluation in relation to the porous medium characterization on which precisely this type of approach opens. The main result, which lies in a quantitative permeability-dependent effective foam mobility, is quite directly and easily exploitable in the framework of augmented Darcy-type models addressing large-scale heterogeneous porous media, and indeed comply with the “if injected with a large gas fraction, foam reduces mobility more in high-permeability layers and diverts flow to low-permeability layers” saying, of which we illustrate quantitatively and as concretely as can be demonstrated by a representative generic minimal model what it is about and the implications.
To sum up, it is an understatement to say that foam flow modelling in porous media still has a long way to go. Until further progress, let us see what works well with geosciences foam flow modelling despite the dizzying change of scale and the hocus-pocus. The paper is organized as follows: first the generic problem to be solved is presented in Section 2 where the notations and driving equations are introduced. In particular it is shown that the emergence of the scaling of foam maximum mobility reduction as the square root of permeability is not limited to a specific Darcy-type model (implicit-texture or population-balance). Section 3 is devoted to the set-up of a minimal model heterogeneous porous medium that is used in Sections 4 (detailed in-situ flow behaviour) and 5 (production data analysis) to study the impact on the flow performance of taking into account such a scaling law by varying the porous medium degree of heterogeneity. The results of a sensitivity analysis are summarized in Section 6. The paper concludes with a discussion in Section 7. A first Appendix A provides elements for estimating the parameters of the considered foam model from measurements while a second Appendix A.2 reports the time evolution of simulated saturation and composition fields related to foam for a few selected configurations which cannot fit in the main text without harming its reading but are however essential to the understanding of foam flow and of the arguments advanced in this work. The simulations presented in this work were carried out with a research version of IFP Energies nouvelles Puma reservoir simulator [8] in which new automatic scaling functionalities have been developed for the only purpose of demonstrating the impact of foam selectivity. Let us first recall the different types of generic foam models considered in geosciences and the scaling law that we propose to test.
2 Darcy-scale model types, driving equations and scaling relationships
2.1 Darcy-scale model types and driving equations
We start with general considerations about three-phase flow in porous media in the presence of foam. We distinguish three phases: an aqueous phase denoted w, a NAPL phase o and a gas phase g. This flow is modified by the presence of foam. Modelling foam requires the presence of surfactant, which is transported by the water phase and requires to solve an additional mass balance equation. Surfactant is either mobile or adsorbed on the rock.
It has been shown that the transport of liquid is not affected by the presence of foam [9–11]. On the opposite, the gas velocity is significantly reduced by the presence of foam. Thus, to describe the water and non-aqueous phases, we consider a “black-NAPL” model (in reference to the “black-oil” model developed in hydrocarbon context [12, 13]) where the gas phase involves a modified velocity denoted 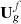 . The mass conservation equations read:
. The mass conservation equations read: (1)where Φ is the rock porosity and the fluxes Jw,
(1)where Φ is the rock porosity and the fluxes Jw, 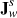 ,
, 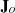 and
and 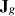 are defined as
are defined as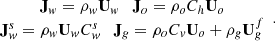 (2)
(2)
For each phase denoted φ = w, o, g, Uφ is the Darcy velocity, Sφ the saturation, ρφ the density and qφ the source/sink term per unit volume of porous medium. The gas phase contains a single volatile component denoted v, whereas the NAPL phase contains a heavy component denoted h and previous volatile component v, with Ch and Cv = 1 − Ch their respective mass fraction in the NAPL phase. The equilibrium constant Kv = 1/Xv, with Xv the molar fraction of volatile component in the NAPL phase, is defined from molar masses of v and h, and mass fractions Cv and Ch. Kv is a function of pressure. 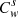 stands for the flowing surfactant mass fraction in the water phase and
stands for the flowing surfactant mass fraction in the water phase and  for the adsorbed surfactant mass fraction on the rock with ρr the rock mass density. Mobile and adsorbed surfactant mass fractions are related with an adsorption law such as the Langmuir isotherm.
for the adsorbed surfactant mass fraction on the rock with ρr the rock mass density. Mobile and adsorbed surfactant mass fractions are related with an adsorption law such as the Langmuir isotherm.
Under creeping (low-velocity) flow conditions, the phase velocities in permeable porous media are governed by the generalized multiphase Darcy’s law [14]: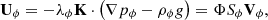 (3)where Uφ is the Darcy velocity, K the porous medium permeability tensor, λφ = krφ/μφ the mobility, μφ the viscosity, pφ the pressure and Vφ = Uφ/(ΦSφ) the interstitial velocity of phase φ [14].
(3)where Uφ is the Darcy velocity, K the porous medium permeability tensor, λφ = krφ/μφ the mobility, μφ the viscosity, pφ the pressure and Vφ = Uφ/(ΦSφ) the interstitial velocity of phase φ [14].
The flow of gas in the presence of foam is modelled differently whether a Population-Balance (PB) or a Semi-Empirical (SE)/Implicit-Texture (IT) modelling approach is used. These models are based on Darcy-type laws which are extended to obtain a modified gas velocity. Most SE/IT foam flow models apply a gas mobility reduction factor when surfactant is present in the water phase. Specifically, the gas mobility  of IT model is scaled by a multi-parameter interpolation function FM assigned to the relative permeability to gas, whereas the gas viscosity is assumed unchanged whether foam is present or not:
of IT model is scaled by a multi-parameter interpolation function FM assigned to the relative permeability to gas, whereas the gas viscosity is assumed unchanged whether foam is present or not: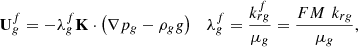 (4)where
(4)where 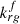 is the modified relative permeability to gas for the IT model in the presence of foam and krg is the conventional relative permeability to gas. Of course, this mobility reduction can also be interpreted as an increase in the viscosity of the gas in the form of foam, as we shall see hereafter for PB models. FM is a multi-parameter interpolation functional form that includes the contributions of physical parameters impacting the gas mobility reduction. FM is formulated as follows:
is the modified relative permeability to gas for the IT model in the presence of foam and krg is the conventional relative permeability to gas. Of course, this mobility reduction can also be interpreted as an increase in the viscosity of the gas in the form of foam, as we shall see hereafter for PB models. FM is a multi-parameter interpolation functional form that includes the contributions of physical parameters impacting the gas mobility reduction. FM is formulated as follows: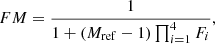 (5)where Mref is the reference (maximum) gas mobility reduction under optimal conditions of the rock-fluid-additive system under consideration, and Fi are functions of four physical parameters that are surfactant concentration, water and NAPL saturations, gas velocity, or equivalently, capillary number. Following [15–17] these functions may be written
(5)where Mref is the reference (maximum) gas mobility reduction under optimal conditions of the rock-fluid-additive system under consideration, and Fi are functions of four physical parameters that are surfactant concentration, water and NAPL saturations, gas velocity, or equivalently, capillary number. Following [15–17] these functions may be written![$$ \begin{array}{ll}{F}_1\left({C}_w^s\right)& ={\left(\frac{\mathrm{min}\left({C}_w^s,{C}_{w,\mathrm{ref}}^s\right)}{{C}_{w,\mathrm{ref}}^s}\right)}^{{e}_s},\\ {F}_2\left({S}_w\right)& =\frac{1}{2}+\frac{1}{\pi }\mathrm{arctan}\left[\mathrm{\Theta }\left({S}_w-{S}_w^{\mathrm{*}}\right)\right],\\ {F}_3\left({S}_o\right)& ={\left(\frac{\mathrm{max}\left(0,{S}_o^{\mathrm{*}}-{S}_o\right)}{{S}_o^{\mathrm{*}}}\right)}^{{e}_o},\\ {F}_4\left(\mathrm{Ca}\right)& ={\left(\frac{\mathrm{C}{\mathrm{a}}_{\mathrm{ref}}}{\mathrm{max}\left(\mathrm{Ca},\mathrm{C}{\mathrm{a}}_{\mathrm{ref}}\right)}\right)}^{{e}_c},\end{array} $$](/articles/stet/full_html/2023/01/stet20220142/stet20220142-eq14.gif) (6)where
(6)where  is the capillary number and σwg the interfacial tension between water and gas. Positive numbers es, Θ, eo and ec drive the shape of F1, F2, F3 and F4 functions, respectively, while
is the capillary number and σwg the interfacial tension between water and gas. Positive numbers es, Θ, eo and ec drive the shape of F1, F2, F3 and F4 functions, respectively, while 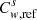 ,
, 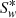 ,
,  and
and 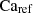 are thresholds. Specifically:
are thresholds. Specifically:
-
Mref can be estimated from the ratio of steady-state measurements of differential pressure across core-plugs, Δpf/Δp, with and without foam, as measured in the laboratory, given that Δp corresponds to a gas injection in the IT model according to (4).
-
F1 function accounts for lamellas stability that is obtained for surfactant concentrations larger than some threshold
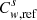 [18, 19].
[18, 19]. -
F2 function governs the sharpness of the transition from the low- to the high-quality regime, through the dimensionless constant Θ, as water saturation decreases in the vicinity of
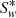 [15–17].
[15–17]. -
F3 function accounts for the impact of the anti-foaming character of NAPL on foam.
-
F4 function accounts for foam shear-thinning (or shear-thickening) behaviour through the capillary number Ca.
Examples of such functions can be found in [15–17, 20] and cited references therein. Estimation of Mref from measurements is detailed in Appendix A. Chemicals natural degradation with time can be accounted for through a half-life time associated to an exponential decay.
The three-phase flow relative permeability to NAPL is classically modelled as a combination of the underlying water/NAPL and gas/NAPL two-phase flow subsystems following Stone’s models [21, 22]. Eventually, the system (1)–(6) with closure relationships ∑Sφ = 1, pcow(Sw) = po − pw and pcog(Sg) = pg − pw, where pcow (pcog) is the capillary pressure between NAPL and water (gas) phases, is solved for the initial boundary value problem in the unknowns pφ(x, t), Sφ(x, t) and 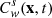 .
.
Population-balance models share the same generalized multiphase Darcy framework but consider foam texture nf, defined as the number of lamellas per unit of foam volume, as an additional unknown to be solved, and a foamed gas viscosity constitutive relationship which depends on nf and adjustable parameters, based on Hirasaki et al [23] extension of Bretherton [24] work to porous media. While it has been shown that PB models are equivalent to IT ones at local steady state [16, 17], they obviously have the advantage, at least in principle (we come back to this below), of being able to better model foam transient generation and collapse which is driven by source terms in the texture transport equation (7) given hereafter. Reviews of such PB models, that are not addressed in this work, can be found in [25, 26]. Here are the main useful features for the work presented here.
Foam mobility is strongly related to its texture which is a key variable in foam modelling in porous media: as foam texture increases, the resistance to gas flow in porous media increases. Population-balance models were designed in order to relate explicitly the gas mobility reduction to the foam texture. Thus, for PB models, the dynamics of foam texture needs to be modelled and a lamella population-balance equation is considered. The impact of foam texture on gas mobility is modelled through an effective gas viscosity and a gas trapping for more elaborated models [11, 27, 28]. The population-balance model involves a lamellas balance that includes lamellas advection at the modified gas velocity and source/sink terms taking into account lamellas creation and destruction [29, 30]. The lamellas population balance equation reads (7)where nf is the foam texture, that is the number of flowing lamellas (or foam bubbles) per unit volume of gas and qf is the external lamellas source/sink term (number of lamellas per unit of time and per unit volume of porous medium). rg and rc are the rates of lamellas creation and coalescence. Different formulas have been proposed in the PB models literature to model these rates [28, 31, 32].
(7)where nf is the foam texture, that is the number of flowing lamellas (or foam bubbles) per unit volume of gas and qf is the external lamellas source/sink term (number of lamellas per unit of time and per unit volume of porous medium). rg and rc are the rates of lamellas creation and coalescence. Different formulas have been proposed in the PB models literature to model these rates [28, 31, 32].
As mentioned earlier, the gas velocity is significantly reduced when foam develops. The viscosity-type PB models extend the generalized Darcy’s equation for the gas phase as follows: (8)where
(8)where 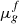 is the effective gas viscosity when flowing as a succession of bubbles. This relationship is similar to (4) but its interpretation and implementation differ. The rheology of PB models of foam flow is classically based on Bretherton’s flow model of a single bubble within a capillary [24], that was later extended by Hirasaki and co-workers to a train of bubbles [23] thus leading to the following expression for the effective gas viscosity:
is the effective gas viscosity when flowing as a succession of bubbles. This relationship is similar to (4) but its interpretation and implementation differ. The rheology of PB models of foam flow is classically based on Bretherton’s flow model of a single bubble within a capillary [24], that was later extended by Hirasaki and co-workers to a train of bubbles [23] thus leading to the following expression for the effective gas viscosity: (9)where Vg is the interstitial gas velocity in the presence of foam. cf is a constant depending on the surfactant concentration and the permeability of the porous medium [33]. The velocity power law involved in the expression of
(9)where Vg is the interstitial gas velocity in the presence of foam. cf is a constant depending on the surfactant concentration and the permeability of the porous medium [33]. The velocity power law involved in the expression of  expresses the shear-thinning effect of flow on foam bubbles. The exponent
expresses the shear-thinning effect of flow on foam bubbles. The exponent 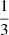 was determined by Bretherton for the motion of a single bubble in a capillary tube with smooth walls [24]. However, for so complex pore geometries as natural porous media, the shear-thinning effect cannot be modelled with the same power law [15].
was determined by Bretherton for the motion of a single bubble in a capillary tube with smooth walls [24]. However, for so complex pore geometries as natural porous media, the shear-thinning effect cannot be modelled with the same power law [15].
In a nutshell, PB models solve foam texture, then foam effective viscosity which depends on the latter by means of a constitutive relationship, and finally phase saturations Sφ and pressures pφ related to the generalized multiphase Darcy framework. While PB models are certainly more consistent from a physical point of view because of the consideration of foam texture that is solved provided source terms rg and rc accounting for foam in-situ generation and collapse in (7) are known, the reality of practice is somewhat different. Conceptually, it is not so much the relation with foam texture steady-state behaviour that is the main plus of PB models, which is well accommodated by IT models although it is not obvious [17], as the local and transient character of foam creation and destruction, driven by rg and rc. In this respect, PB models are good research tools. However, for the time being, when considering natural porous media it remains tricky to take advantage of this benefit of PB models because foam local and time-dependent generation and collapse, modelled by source terms rg and rc, are intimately related to the pore-scale structure of the porous medium (involved in leave-behind, snap-off, and lamella division mechanisms), which again is difficult to determine accurately at large geological scales. Thus, rather paradoxically, in practice PB models may not provide more predictivity but more degrees of freedom and require solving one more (texture) equation compared to IT models. Given that PB models are equivalent to IT models at local equilibrium steady state, setting rg = rc in (7) [16, 17], this assumption not being intended to be general but remaining the simplest to make in practice for lack of anything better, it is legitimate to wonder about the advantage of considering PB models to simulate foam-based displacements in natural porous media which are intrinsically uncertain. Notwithstanding, it is certainly not the model but the determination and the taking into account of the structure of the porous medium at small scales nested in large ones which is an issue and leads to rather conservative and basic choices in practice.
To finish with, IT models account for foam apparent viscosity that may be written (10)and depends on foam quality fg = |Ug|/|U|, where the total velocity U = ∑Uφ is the sum of the phase velocities. When plotted as a function of fg,
(10)and depends on foam quality fg = |Ug|/|U|, where the total velocity U = ∑Uφ is the sum of the phase velocities. When plotted as a function of fg,  has the shape of an asymmetrical bell curve that is maximum for the optimal quality
has the shape of an asymmetrical bell curve that is maximum for the optimal quality 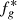 in the neighborhood of which the sharpness of the transition from the low- to the high-quality regime is driven by the F2 function (6). This is a key feature for assessing foam in porous media (see [15, 16] and cited references therein for calibration examples).
in the neighborhood of which the sharpness of the transition from the low- to the high-quality regime is driven by the F2 function (6). This is a key feature for assessing foam in porous media (see [15, 16] and cited references therein for calibration examples).
In any case, given that each model has specific drawbacks and little predictive capability due to the large number of parameters that need to be adjusted beforehand, the following scaling law considerations, while developed in the context of IT models, also apply to PB models under the assumption of local equilibrium steady state.
2.2 Scaling relationships
Now we focus on the effect of permeability on foam properties. Many observations have been made by several authors, especially [34–37] in the context of oil recovery, but also in other contexts that will not be reviewed herein. Regarding soil remediation however, it is worth citing a laboratory study on a two-layer stack of porous media that evidenced the selective nature of foam [4]. In the field of enhanced oil recovery, a laboratory and phenomenological simulation study has been performed by considering simplified heterogeneous porous media, with most emphasis on chemistry however [38]. Eventually, a recent work based on laboratory measurements analysis and physical interpretation within the framework of implicit-texture modelling has brought new trends for foam main drivers with respect to permeability, assuming porous media to be homothetic [15]. As the present paper is a companion of this previous published work, the reader is referred to it for further details that cannot be given here. Here are the main findings useful for this work.
For a given foam, the mobility reduction Mref represents the ratio between the continuous gas mobility krg/μg and the foamed-gas mobility that is defined as 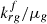 in IT models, or as
in IT models, or as 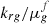 in PB models, at optimal foaming conditions. Scaling Mref for different porous media characterized by the same krg function can then be reduced to the scaling of
in PB models, at optimal foaming conditions. Scaling Mref for different porous media characterized by the same krg function can then be reduced to the scaling of 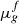 . Analogy between flow in a capillary tube (originally formulated by Bretherton [24]) and flow in a porous medium has led most authors to use the empirical rheological law given by (9) for foamed-gas.
. Analogy between flow in a capillary tube (originally formulated by Bretherton [24]) and flow in a porous medium has led most authors to use the empirical rheological law given by (9) for foamed-gas.
Kovscek and Bertin [33] derived an expression of  scaled with respect to rock permeability and capillary pressure by establishing an equivalence between rheological law given by (9) and Hirasaki and Lawson’s formula for the apparent viscosity of a train of bubbles of pre-determined volume flowing in a capillary tube, that is [23]:
scaled with respect to rock permeability and capillary pressure by establishing an equivalence between rheological law given by (9) and Hirasaki and Lawson’s formula for the apparent viscosity of a train of bubbles of pre-determined volume flowing in a capillary tube, that is [23]: (11)where R is the tube radius and Rc the curvature radius of the Plateau borders [18] separating gas bubbles and nf the lineic foam texture, i.e. the number of lamellas per flow-length unit. This formula assumes that touching bubbles are flowing through the capillary and that the surface tension gradient effects on effective gas viscosity are negligible. Actually, that expression of the effective viscosity can be considered for scaling purpose, because it is related to the geometrical characteristics of capillary tubes, or to the properties of the equivalent porous medium represented as a bundle of such capillary tubes.
(11)where R is the tube radius and Rc the curvature radius of the Plateau borders [18] separating gas bubbles and nf the lineic foam texture, i.e. the number of lamellas per flow-length unit. This formula assumes that touching bubbles are flowing through the capillary and that the surface tension gradient effects on effective gas viscosity are negligible. Actually, that expression of the effective viscosity can be considered for scaling purpose, because it is related to the geometrical characteristics of capillary tubes, or to the properties of the equivalent porous medium represented as a bundle of such capillary tubes.
For a given foam flowing in a porous medium of permeability K and porosity Φ, capillary tube radius R is equivalent to the quantity 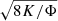 and Rc is related to the disjoining pressure of the films of the foam under consideration [39]. Rc is therefore assumed invariant for the same foam displaced through different porous media. Furthermore, we assume that Rc is negligible compared to pore radii (such an assumption may not be valid however in very-low-permeability media). Therefore,
and Rc is related to the disjoining pressure of the films of the foam under consideration [39]. Rc is therefore assumed invariant for the same foam displaced through different porous media. Furthermore, we assume that Rc is negligible compared to pore radii (such an assumption may not be valid however in very-low-permeability media). Therefore, 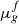 scales as nfR2 under given velocity conditions. For homothetic porous media of different permeabilities with similar porosities, R scales as
scales as nfR2 under given velocity conditions. For homothetic porous media of different permeabilities with similar porosities, R scales as 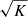 and the lineic foam texture nf, that is proportional to 1/R [15], scales as
and the lineic foam texture nf, that is proportional to 1/R [15], scales as  , hence
, hence 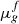 scales as
scales as  . The above analysis indicates that Mref is expected to increase as the square root of permeability for homothetic porous media of different permeabilities:
. The above analysis indicates that Mref is expected to increase as the square root of permeability for homothetic porous media of different permeabilities: (12)
(12)
That scaling approximation neglects small porosity variations compared to permeability variations in many natural porous media, and is the main trend that emerges among the scaling trends reported in [15] that are reproduced in Table 1.
It is worth mentioning that aquifer permeability are commonly much higher than oil reservoir ones. Aquifer permeability can be very high, ranging from a few Darcies to hundreds of Darcies. When K is high, the scaling relationship (12) is questionable because it is based roughly on the assumption that the characteristic length of the gas bubble is of same order than pore length (one bubble per pore). This assumption is not true when permeability is high and there are several bubbles per pore.
Probing the impact of that Mref scaling at the reservoir scale is the purpose of this work, with implications on the assignment of Mref values to rock-types in reservoir models.
3 Model case study set-up
3.1 General considerations related to the scaling with respect to permeability
Scaling law (12) highlights the role that foam can play as a NAPL displacing fluid in heterogeneous porous media. If, as an example, we represent schematically the porous medium under consideration as a stack of layers1, high-permeability layers may lead to a by-pass of low-permeability ones when a fluid (say water or gas) is injected to flush NAPL. Thus, remaining NAPL in low-permeability layers remains trapped and may constitute a primary target for foam, not in a frontal displacement perspective but rather as foam blocking selectively the flow in more permeable layers thus generating fluid diversion in low-permeability layers. It is precisely the diverted fluid (water and/or gas), and not necessarily foam itself, that will displace the trapped NAPL in low-permeability zones. It is thus more a problem of conformance control than of displacement. Before moving on to the set-up of the toy porous medium used to evidence the impact of foam mobility reduction scaling with respect to permeability, described in Section 3.3, let us return to the scaling law (12) to account for permeability anisotropy and raise some practical questions.
Any feasibility study implies measurements, here foam injections practiced on cores, assuming that an adequate chemistry has been developed for the conditions of pressure, temperature and brine salinity of the porous medium under consideration. As such, the question of cores selection is raised: on which core samples would it be necessary to characterize foam beforehand? Ultimately, how many measurements are needed? Obviously, scaling law (12) may guide a smart core sampling in relation to the porous medium heterogeneity characterization, rock-type per rock-type.
For the sake of demonstration, let us assume the layer-cake reservoir overall average horizontal permeability is  mD where hi is the ith layer height,
mD where hi is the ith layer height,  is the ith layer horizontal permeability and H = ∑ hi is the height of the reservoir interval. Let us further assume the interpretation of laboratory foam displacements on core-plugs yields, among other things, a reference mobility reduction of Mref = 500 for that permeability 〈Kx〉 = 100 mD, and most of the potential issues related to foam have been solved, e.g. it does not drain/collapse too quickly and surfactant does not adsorb too much on the rock (this is not the question asked here but these are strong assumptions).
is the ith layer horizontal permeability and H = ∑ hi is the height of the reservoir interval. Let us further assume the interpretation of laboratory foam displacements on core-plugs yields, among other things, a reference mobility reduction of Mref = 500 for that permeability 〈Kx〉 = 100 mD, and most of the potential issues related to foam have been solved, e.g. it does not drain/collapse too quickly and surfactant does not adsorb too much on the rock (this is not the question asked here but these are strong assumptions).
In the minimal layer-cake example discussed in this paper, whose reservoir structure and heterogeneity are detailed below in Section 3.3, we propose to quantify the impact of taking into account a dependence of the foam mobility reduction on the permeability, following scaling law (12), on NAPL removal. Such a scaling law practice is common for capillary pressure and (less often) for chemicals adsorption, which both2 scale as 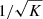 .
.
Let us then consider a layer-cake reservoir of fixed average horizontal permeability, say 〈Kx〉 = 100 mD to which is assigned a mobility reduction of Mref = 500, with contrasts in permeability from one layer to another. This contrast is varied from one realization to another in order to probe the foam flow behaviour on independent configurations whose heterogeneity degree varies gradually, from very large to moderate deviations to the average permeability (preserving the mean), and illustrate the implications of Mref scaling on the assignment of Mref values to rock-types in reservoir models. In each case, Mref is associated with Kref and the mobility reduction is computed for each cell of the reservoir mesh following (12) as: (13)
(13)
According to this relationship, fixing Kref and varying the assigned Mref is equivalent to fixing Mref and varying the associated Kref. Thus, varying the Mref value associated with Kref = 100 mD, say either Mref = 500 or 1581, is equivalent to assigning Mref = 500 to either Kref = 100 or 10 mD, respectively. These two examples will be considered hereafter.
Let us now consider how to manage the directional character of the flow in relation to the permeability tensor K. In the simplest layer-cake geometry where the layers are all flat and parallel (they can however be tilted), the permeability tensor is diagonal in the Cartesian coordinate system (x, y, z) such that the x and y coordinates span the geological layers, thus K =d iag(Kx, Ky, Kz) and (13) reads for the scaled mobility reduction: (14)
(14)
This relation writes identically if the layers are not flat but parabolic (as in the case of an anticline structure) or of any shape in relation to a deposit structure, by substituting to the Cartesian coordinate system (x, y, z) the curvilinear one that spans the layers. Doing so, the mobility function FM given by (5) also acquires a directional character upon Mref scaling, and it will now be denoted as follows: (15)
(15)
As the vertical permeability Kz usually differs from the horizontal one Kx (assuming Kx = Ky for the considered simple layer-cake geometry), which is driven by the anisotropy ratio Kz/Kx, so do the reference permeabilities Kref,z and Kref,x, and the mobility reductions Mref,z and Mref,x, FMz and FMx in the corresponding directions.
To finish with, we do not consider chemicals adsorption nor the impact of NAPL on foam in this work since they both primarily impact economics and chemicals slug size, which is not the topic addressed here. Of course, they are of critical interest for technical and economical evaluation (the reader is referred to [20] for such an evaluation for naturally fractured oil-wet reservoirs, e.g.). It is also assumed that the reservoir can withstand the imposed injection flow rate without suffering from any injectivity issues due to pressure build-up. This is in practice one of the key points to be addressed for any viscous fluid injection in low-permeability formations, but since we assume the existence of very permeable layers as detailed in Section 3.3, this assumption remains reasonable. It is worth noting that the injectivity of shear-thinning (or shear-thickening) fluids whose viscosity varies a lot for large velocity gradients in the near-wellbore, as it can be the case of pre-formed foam or polymer solution, requires a specific treatment of injectivity and productivity indices [40] whose traditional formulation presupposes a constant viscosity over the well gridblock [41], which underestimates the injectivity of shear-thinning fluids.
Commingled foam injection is considered first as a baseline prior to any selective injection: gas and surfactant solution are injected over the full 50 m height perforated reservoir interval (see Sect. 3.3), not in a specific layer. The permeability tensor with components Kx(x, z) and Kz(x, z) is considered either isotropic or strongly anisotropic, i.e. Kz/Kx = 1 or 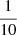 , respectively, where Kz(x, z) is deduced from Kx(x, z) which is geostatistically generated by imposing a constant mean 〈Kx〉 = 100 mD, as explained in Section 3.3. Two types of injection are considered: either a co-injection of surfactant solution and gas (with a quality of fg = 0.8) which corresponds to a pre-formed foam injection, and surfactant solution alternating gas injection for which foam is formed in-situ, as reported in Figure 1, with an imposed constant total injection flow rate of 54.8 m3/day for which one pore volume (PV) of the reservoir is injected within one year. Indeed, since foams are not a proven large-scale recovery process, the mode of fluids injection is also being investigated, with the literature reporting roughly as many co-injection tests as alternate injection. However, pre-formed foam injection may be preferred for fractured reservoirs with poor in-situ foam generation mechanisms in the fracture network. In both cases, 0.25 PV of a 5000 ppm concentrated surfactant solution is injected. All the simulations are performed with IFP Energies nouvelles reservoir simulator Puma, which accounts for the above-mentioned foam features, including the Mref scaling law relationships (14) and (15) (see [15] and cited references therein).
, respectively, where Kz(x, z) is deduced from Kx(x, z) which is geostatistically generated by imposing a constant mean 〈Kx〉 = 100 mD, as explained in Section 3.3. Two types of injection are considered: either a co-injection of surfactant solution and gas (with a quality of fg = 0.8) which corresponds to a pre-formed foam injection, and surfactant solution alternating gas injection for which foam is formed in-situ, as reported in Figure 1, with an imposed constant total injection flow rate of 54.8 m3/day for which one pore volume (PV) of the reservoir is injected within one year. Indeed, since foams are not a proven large-scale recovery process, the mode of fluids injection is also being investigated, with the literature reporting roughly as many co-injection tests as alternate injection. However, pre-formed foam injection may be preferred for fractured reservoirs with poor in-situ foam generation mechanisms in the fracture network. In both cases, 0.25 PV of a 5000 ppm concentrated surfactant solution is injected. All the simulations are performed with IFP Energies nouvelles reservoir simulator Puma, which accounts for the above-mentioned foam features, including the Mref scaling law relationships (14) and (15) (see [15] and cited references therein).
 |
Fig. 1 Timeline of surfactant solution/gas co-injection (blue) and surfactant solution alternating gas injection (red) scenarios, where W, G and W* denote water, gas and surfactant solution, respectively. Timescale is indicated in injected pore volumes (PV, volume of fluid injected over the pore volume of the porous medium). Both cases have a pre-foam water or gas injection history of 1 PV. In each case the volume of surfactant solution injected of 0.25 PV is identical: in the co-injection case, it is distributed over a total volume of gas and surfactant solution of 1.25 PV according to the imposed quality of fg = 0.8 that corresponds to optimal foaming conditions. There is no such quality control for the surfactant solution alternating gas injection, where foam is formed by fingering of gas (injected after surfactant solution) through surfactant solution, or at least mixing of the two, due to the different mobility of the fluids. |
3.2 Rock-fluid properties
The reservoir under consideration has an average temperature of Tres = 100 °C and an average pressure of pres = 100 bar. Rock-fluid properties are representative of Berea sandstone with a foam made up of a surfactant aqueous solution and a methane/CO2 mixture (62% CO2, 38% CH4) with a quality fg = 0.8. The reader is referred to the previous work [42] for further details. These conditions are far from near-subsurface aquifer ones where the temperature is close to 15 °C and the pressure is about a few bar. In the same vein, the gas that will be used to generate foam for soil remediation will be nitrogen or simply air. However, these points have no bearing on the work presented, which remains phenomenological in nature.
Three-phase flow is modelled as a combination of the underlying water/NAPL and gas/NAPL two-phase subsystems following Stone I model [21, 22]. Water is considered as the wetting phase while gas is the non-wetting phase, NAPL being the common and intermediate phase to both subsystems. Each two-phase subsystem is set up symmetrically with respect to its wetting phase following Brooks-Corey relationships [43, 44], assuming power-law relative permeabilities and capillary pressures. Relative permeabilities to water and NAPL, krw and krow, and capillary pressure pcow = po − pw, depend on the normalized mobile water saturation SW = (Sw − Swi)/(1 − Sorw − Swi), and read: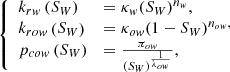 (16)where Swi is the irreducible water saturation, Sorw is the residual NAPL saturation with respect to water, κw and κow are the maximum relative permeabilities to water and NAPL, and πow is the entry capillary pressure. The gas/NAPL subsystem, for which NAPL is the wetting phase, is set up symmetrically as a function of the normalized mobile gas saturation SG = (Sg − Sgr)/(1 − Sorg − Swi − Sgr):
(16)where Swi is the irreducible water saturation, Sorw is the residual NAPL saturation with respect to water, κw and κow are the maximum relative permeabilities to water and NAPL, and πow is the entry capillary pressure. The gas/NAPL subsystem, for which NAPL is the wetting phase, is set up symmetrically as a function of the normalized mobile gas saturation SG = (Sg − Sgr)/(1 − Sorg − Swi − Sgr):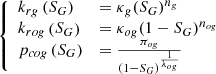 (17)with pcog = pg − po and where Sgr is the irreducible gas saturation and Sorg is the residual NAPL saturation with respect to gas. Figure 2 shows flow curves (16) and (17) with parameters given in Table 2.
(17)with pcog = pg − po and where Sgr is the irreducible gas saturation and Sorg is the residual NAPL saturation with respect to gas. Figure 2 shows flow curves (16) and (17) with parameters given in Table 2.
 |
Fig. 2 Water/NAPL and gas/NAPL two-phase subsystems power-law relative permeabilities and capillary pressures (16) and (17) with parameters given in Table 2. |
To finish with, the specific choice of Stone’s model is arbitrary and only justified by its widespread use in reservoir engineering. This “choice of the majority” puts a restriction on the work carried out and would merit further specific investigations related to foam flow, disentangling properly transport and adsorption, that are out of the scope of the present work.
3.3 Model layered porous medium set-up
The reservoir under consideration is a two-dimensional cross-sectional x-z layered porous medium of 200 m length, 50 m height and 10 m width3. Porosity is set constant to Φ = 0.2. The average horizontal permeability in the x-coordinate is set constant to 〈Kx〉 = 100 mD while the permeability anisotropy ratio Kz/Kx, from which the vertical permeability Kz is deduced, is set to either  (strongly anisotropic) or 1 (isotropic). Several permeability map realizations Kx(x, z) of increasing degree of heterogeneity are considered. They range from quasi-homogeneous to highly heterogeneous by varying the horizontal permeability standard deviation
(strongly anisotropic) or 1 (isotropic). Several permeability map realizations Kx(x, z) of increasing degree of heterogeneity are considered. They range from quasi-homogeneous to highly heterogeneous by varying the horizontal permeability standard deviation 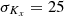 , 50, 100, 150, 200, 250 mD, as reported in Figures 3 and 4, using a fast Fourier transform moving average algorithm [45, 46].
, 50, 100, 150, 200, 250 mD, as reported in Figures 3 and 4, using a fast Fourier transform moving average algorithm [45, 46].
 |
Fig. 3 Comparison of several two-dimensional horizontal permeability field Kx(x, z) realizations (approximately log-normal distributed) with constant mean 〈Kx〉 = 100 mD and standard deviation |
 |
Fig. 4 Comparison of several two-dimensional horizontal permeability field Kx(x, z) realizations (approximately log-normal distributed) with constant mean 〈Kx〉 = 100 mD and standard deviation |
In each case, Kx(x, z) is approximately log-normal distributed with a constant mean 〈Kx〉 = 100 mD. Layers typical thickness over which Kx(x, z) is approximately constant is controlled by a Gaussian auto-correlation function whose correlation length Lz in the z-coordinate is set to 10 or 5 m, while the correlation length in the x-coordinate is arbitrarily large (Lx = 1000 m) in order to render a layer-cake with excellent lateral continuity. Under these conditions, the characteristic layers thickness is close to the correlation length Lz, and we will abuse the language by sometimes referring to Lz as the typical layers thickness.
The degree of heterogeneity in permeability may be quantified by the Dykstra-Parsons coefficient [47] defined as VDP = (e
μ
− e
μ
−
σ
)/e
μ
= 1 − e−σ) for a log-normal random variable K of parameters μ = 〈ln K〉 and σ2 = 〈(lnK − μ)2〉. VDP writes in terms of the permeability mean 〈K〉 and variance  as4:
as4:![$$ {V}_{\mathrm{DP}}=1-\mathrm{exp}\left(-\sqrt{\mathrm{ln}\left[1+{\left(\frac{{\sigma }_K}\left\langle K\right\rangle\right)}^2\right]}\right), $$](/articles/stet/full_html/2023/01/stet20220142/stet20220142-eq61.gif) (18)where the subscript x has been dropped for the sake of readability. Thus, VDP → 0 for a homogeneous permeability distribution such that σK/〈K〉 → 0 whereas VDP → 1 for an extremely heterogeneous distribution with σK/〈K〉 → ∞. Above-mentioned permeability standard deviations of
(18)where the subscript x has been dropped for the sake of readability. Thus, VDP → 0 for a homogeneous permeability distribution such that σK/〈K〉 → 0 whereas VDP → 1 for an extremely heterogeneous distribution with σK/〈K〉 → ∞. Above-mentioned permeability standard deviations of 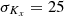 , 50, 100, 150, 200, 250 mD are equivalent to the Dykstra-Parsons coefficients VDP = 0.22, 0.37, 0.57, 0.66, 0.72, 0.75, as indicated in Figures 3 and 4. The mesh is discretized in x- and z-coordinate with 100 and 50 cells, respectively; cells are therefore of constant size of 2 × 1 m thus the mesh is really very refined. Injection and production wells are located at the boundaries x = 0 and 200 m respectively, and are both perforated over all the layers for all z ∈ [0, H]. No-flow conditions are assigned to the top and the bottom of the layer-cake z = 0 and H.
, 50, 100, 150, 200, 250 mD are equivalent to the Dykstra-Parsons coefficients VDP = 0.22, 0.37, 0.57, 0.66, 0.72, 0.75, as indicated in Figures 3 and 4. The mesh is discretized in x- and z-coordinate with 100 and 50 cells, respectively; cells are therefore of constant size of 2 × 1 m thus the mesh is really very refined. Injection and production wells are located at the boundaries x = 0 and 200 m respectively, and are both perforated over all the layers for all z ∈ [0, H]. No-flow conditions are assigned to the top and the bottom of the layer-cake z = 0 and H.
To finish with, it is worth mentioning the question of flow direction with respect to strata in a stratified system (which is already a limitation, since, in the case of NAPL problems, many shallow aquifers are not necessarily simple layered systems) is rather tricky. This work is restricted to the minimal complexity of a stratified bedding in order to quantify the coupling of foam viscous flow with heterogeneity. In practice, many configurations can arise, ranging from a very thick homogeneous shallow aquifer-type reservoir interval to heterogeneous puzzle-type geometries, with well architectures of varying complexity, that are not addressed in the present work.
4 Numerical simulations
We now compare foam flow performance on NAPL removal, depending on whether foam is pre-formed under co-injection of surfactant solution and gas, or forms in-situ under surfactant solution alternating gas injection, according to the injection scenarios given in Figure 1. The foam maximum mobility reduction Mref is scaled in relation to the porous medium permeability distribution following (14) and (15), or not. Both injection scenarios (co-injection or alternate injection) have a pre-foam water or gas injection history of one injected pore volume in order to diagnose flow performance under water or gas flooding, to identify the reservoir unswept zones and to anticipate the contribution that foam would have. In each case the 0.25 PV volume of surfactant solution injected is identical: in the co-injection case, it is distributed over a total volume of gas and surfactant solution of 1.25 PV according to the imposed quality of fg = 0.8 that corresponds to optimal foaming conditions. There is no such quality control for the surfactant solution alternating gas injection, where foam is formed by fingering of gas (injected after surfactant solution) through surfactant solution, or at least mixing of the two, due to the different mobility of the fluids. The two-dimensional x-z layer-cake porous medium under consideration is initially saturated with NAPL up to the irreducible water saturation5 Swi given in Table 2. We proceed as follows:
-
A mobility reduction of either Mref,x = 500 or 1581 is assigned to the reference horizontal permeability Kref,x = 100 mD that is equal to the reservoir average horizontal permeability 〈Kx〉. As explained in Section 3.1, this is equivalent to assigning Mref,x = 500 to either Kref,x = 100 or 10 mD, respectively. This will give two configurations for further comparisons.
-
The permeability tensor with components Kx(x, z) and Kz(x, z), is considered either isotropic or strongly anisotropic setting either Kz/Kx = 1 or
 , where Kz(x, z) is deduced from Kx(x, z) which is geostatistically generated by imposing a constant mean 〈Kx〉 = 100 mD, as explained in Section 3.3.
, where Kz(x, z) is deduced from Kx(x, z) which is geostatistically generated by imposing a constant mean 〈Kx〉 = 100 mD, as explained in Section 3.3. -
Several two-dimensional horizontal permeability field Kx(x, z) realizations (approximately log-normal distributed) are considered by imposing the mean 〈Kx〉 = 100 mD and varying the standard deviation
 , 50, 100, 150, 200, 250 mD, or equivalently, the Dykstra-Parsons coefficient VDP = 0.22, 0.37, 0.57, 0.66, 0.72, 0.75, as shown in Figures 3 and 4.
, 50, 100, 150, 200, 250 mD, or equivalently, the Dykstra-Parsons coefficient VDP = 0.22, 0.37, 0.57, 0.66, 0.72, 0.75, as shown in Figures 3 and 4. -
Typical layers thickness driven by and close to the correlation length Lz of either 10 or 5 m are considered.
To start with, in-situ foam flows without and with Mref scaling are compared in the two following Sections 4.2 and 4.3 for the largest Dykstra-Parsons coefficient VDP = 0.75 for foam flooding obtained under co-injection of surfactant solution and gas or surfactant solution alternating gas injection. The initial in-situ behaviour under water or gas flooding is first analyzed in Section 4.1. Figures that compare the in-situ dynamic behaviour of saturations Sw, Sg, So, foaming agent concentration Cf, mobility reduction function in the x-coordinate (FMx)−1, as well as the horizontally and vertically averaged corresponding profiles, have been moved in Appendix A.2 for the sake of readability.
Production data such as NAPL recovery, produced chemicals and gas including chemicals breakthrough time, are compared in Sections 5. Eventually, flow performance with and without Mref scaling are compared in Section 6 and characterized by sweep trends in relation with the Dykstra-Parsons coefficient.
4.1 Flow performance baseline without foam
To start with, let us analyze the flow without chemical additives, i.e. without foam, considering the two injection scenarios given in Figure 1, co-injection of water and gas or water alternating gas injection, without surfactant in the water phase. This baseline will serve as a comparison point for simulated foam flows with and without Mref scaling, which will also be compared with each other.
Very classically, we find the following well-known result: all other things being equal, the higher the reservoir degree of heterogeneity that is transcribed by VDP, the lower the vertical sweep of the reservoir by water and/or gas flooding. This can be seen very clearly on NAPL production curves shown in (top) Figures 5a and 8a: as VDP increases from 0.22 to 0.75 (see Figs. 3 and 4), the final NAPL recovery, expressed as the ratio of the cumulative volume of NAPL recovered over the initial volume of NAPL in place, drops from 70% to 30%, approximately. In the most heterogeneous case VDP = 0.75, only the most permeable fraction of the reservoir is swept as shown in Figure A1. Once the injected displacing fluid has broken through to the producing well, a large fraction of the reservoir is hydraulically bypassed and will mostly remain so, as evidenced by the very slow NAPL recovery late-time evolution reported in Figures 5a and 8a which reflects the late-time microscopic displacement efficiency, due to the propagation in the most permeable layers of the very loose tail of the displacing saturation front that relaxes very slowly and is very inefficient in NAPL mobilization. Put more simply: once the displacement front has broken through, not much happens, or at least very slowly.
 |
Fig. 5 Co-injection case with Mref,x = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
 |
Fig. 6 Co-injection case with Kref,x = 100 mD, (a) Mref,x = 500, (b) Mref,x = 1581 (or equivalently Mref,x = 500, (a) Kref,x = 100 mD, (b) Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of produced cumulative gas volume (Vg) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
 |
Fig. 7 Co-injection case with Mref,x = 1581, Kref = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
 |
Fig. 8 Alternate injection case with Mref,x = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
 |
Fig. 9 Alternate injection case with Mref,x = 1581, Kref,x= 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
 |
Fig. 10 Comparison of the maximum NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) relative variation under foam flooding with scaled Mref,x relatively to constant Mref, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
 |
Fig. 11 Comparison of the (a) final produced surfactant cumulative mass (Mf) and (b) chemicals breakthrough time (BT) relative variation under foam flooding with scaled Mref,x relatively to constant Mref,x, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
 |
Fig. 12 Comparison of the produced cumulative gas volume (Vg) relative variation under foam flooding with scaled Mref,x relatively constant Mref,x, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
 |
Fig. 13 Comparison of the differential behaviour of production results under foam flooding with scaled Mref,x relatively to constant Mref,x as a function of the injection sequence (co-injection or alternate injection), VDP = 0.22, 0.37, 0.57, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz (subscripts “ani” and “iso” stand for Kz/Kx = 0.1 and 1 while “Lz” and “Lz/2” correspond to Lz = 10 and 5 m, respectively). |
 |
Fig. 14 Comparison of the differential behaviour of production results under foam flooding with scaled Mref,x relatively to constant Mref,x as a function of the injection sequence (co-injection or alternate injection), VDP = 0.66, 0.72, 0.75, Kref,x =100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz (subscripts “ani” and “iso” stand for Kz/Kx = 0.1 and 1 while “Lz” and “Lz/2” correspond to Lz = 10 and 5 m, respectively). |
We will not go into further detail on this well-known type of behaviour which has been the subject of much work [48–50] and it should be retained, since the sweep efficiency generally writes as the product of the macroscopic (here vertical) and microscopic sweep efficiencies, how crucial it is to improve the volumetric sweep (vertical and/or areal) when addressing very heterogeneous porous media, because otherwise whatever the improvement in the microscopic displacement efficiency (by increasing the displacing fluid viscosity and/or modifying the interfacial rock-fluids capillary forces), it may concern only a tiny volumetric fraction of the porous medium under consideration. For example, Figures 5a and 8a clearly illustrate, for VDP = 0.22 (very moderate heterogeneity), the impact of the displacing fluid viscosity, depending on whether it is water or gas, on the transient early-time NAPL recovery: water indeed presents a much larger displacement saturation front than gas (assumed here to be immiscible with NAPL), mostly due to the difference in viscosity, thus the transient early-time NAPL recovery is more efficient and much faster for water than for gas flooding. It will also take much longer for gas than for water flooding to reach a pseudo steady state such that the tail of the displacing saturation front has completely relaxed, as saturation levels of NAPL to be displaced by the tail at the back of the displacing saturation front are larger for gas flooding, with the practical difference that in general gas injects more easily than water, again due to its viscosity (however, this is not the case for the simulations presented which were carried out at an imposed flow rate).
It is worth noting that in moderate to low VDP configurations, the vertical sweep is much better because more and more layers are accessible to the flow and are swept, which is enhanced by the alternating injection of a dense fluid (water) and a less dense fluid (gas), known as WAG for water alternating gas, in order to compensate for gravity segregation and poor vertical sweep that can follow independently of heterogeneity. Co-injection of water and gas, which is equivalent to the limiting case of infinitesimal alternating water and gas slugs, is obviously much more efficient in NAPL recovery kinetics as can be seen by comparing Figures 5a and 8a, because of fluids gravity segregation which is permanently compensated, unlike the water alternating gas injection, the NAPL recovery of which is done in two stages, as shown in Figure 8a, which correspond to the propagation of gas then water. In the very heterogeneous cases, the mitigation of gravity segregation by co-injecting or alternating water and gas is much less efficient as heterogeneity rules. This trend, which however is not a general rule and depends on the height of the most permeable layers and inter-well spacing, is very clear in Figure 8a as VDP increases.
This is a quite classic and predictable behaviour that foam is precisely expected to remedy. We will indeed show that the more heterogeneous the reservoir is (the higher VDP is), the smaller the vertical sweep of the reservoir by water or gas is (only the most permeable layers are swept), but the more efficient foam is and the better the incremental vertical sweep and NAPL recovery are compared to a twin injection type without foam (without surfactant). Let us see why and how.
4.2 Comparison of in-situ foam flow with and without Mref scaling: co-injection
We now focus on foam injection in the form of a 1.25 PV co-injection of surfactant solution and gas that follows a 1 PV water injection, and continues with a 1.75 PV water injection again, as indicated in Figure 1. Due to the imposed quality fg = 0.8, the co-injection of surfactant solution and gas consists of a 0.25 PV surfactant solution slug. The behaviour of the pre-foam water injection has been commented in the previous section. Let us see now what the foam brings.
Figures A1, A2 and A3 compare the in-situ dynamic bevaviour of foam flow (i) after 1 PV of water injection prior to surfactant injection, (ii) after 0.25 PV of surfactant injection (end of the surfactant injection), and (iii) at the end of the full injection sequence, without and with Mref scaling, for VDP = 0.75, Mref = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m.
After 1 PV of water injection, the most permeable central layer has been well swept, as can be seen from water and NAPL saturation profiles. This layer clearly dominates the flow so that the rest of the reservoir is little swept, as evidenced in Figure A1.
After 0.25 PV of surfactant solution injection, foam has propagated in the most permeable layers where there is preferential flow as shown by the mobility reduction function component (FMx)−1 in Figure A2 that is much larger in high-permeability layers when scaling Mref compared to a constant Mref, and, on the contrary, that is smaller in the less permeable layers. With a constant Mref, the surfactant concentration profile mostly invades the zones that were previously swept by water, that is mainly the most permeable layers and a small fraction of the less permeable peripheral layers. An improvement in the sweeping of the latter can be noted, which did not occur after the 1 PV water injection and which would certainly not have occured if the water injection had been continued. In addition, the dominant drain is better swept microscopically compared to water flooding due to the sharp increase in the displacing foamed gas saturation front, as can be seen from the NAPL saturation profile, and which is the first expected effect according to a classic Buckley-Leverett calculation [14, 49–51].
Alternatively, it can be noted qualitatively from the saturation profiles that the in-situ quality of the foam is very different from the quality imposed at the injection well of fg = 0.8. While this is due to the coupling of the differential behaviour of the phases mobilities and reservoir heterogeneity (and also capillary trapping), it may raise a question about the conclusions that can be drawn from laboratory evaluations by core-scale displacements, where the quality is often imposed and constant, all the more so at steady state. At least, the inevitable variation of fg in the reservoir implies paying special attention to the behaviour of the foam apparent viscosity as a function of fg, and it would obviously be desirable that the latter varies little in the neighborhood of the optimal foam quality 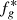 . In any case this is monitorable by simulation provided that a reliable and accurate characterization of the rock-fluids system is available, and that on-site pilot tests are suitably instrumented for monitoring purposes.
. In any case this is monitorable by simulation provided that a reliable and accurate characterization of the rock-fluids system is available, and that on-site pilot tests are suitably instrumented for monitoring purposes.
When scaling Mref, (FMx)−1 increases in the most permeable layer while it decreases in the low-permeable ones, compared to a constant Mref, as expected from (14) and (15). This leads to a more significant invasion of the peripheral layers as can be seen from the surfactant concentration and water, gas and NAPL saturation profiles in Figure A2.
At the end of the 0.25 PV surfactant injection, the profiles shown in Figure A3 are very different when comparing a constant Mref to a scaled one. One can observe an almost complete desaturation of the central drain in both cases, but above all a much better sweep of the peripheral layers due to a redistribution of the flow from the central drain when Mref is scaled. The differences in surfactant concentration and saturation profiles are very significant in the peripheral layers and are not primarily due to differences in (FMx)−1 values in the peripheral layers, which are roughly speaking close there whether Mref is scaled or not.
Eventually, at the end of the total injection sequence shown in Figure A3, surfactant has been evacuated from the central drain (which again behaves like a bypass) and remains further trapped in the peripheral layers when Mref is scaled, which is consistent with the previously observed flow redistribution.
A similar behaviour is observed when considering Mref,x =1581 and Kref,x = 100 mD (or equivalently Mref,x = 500 and Kref,x = 10 mD), as reported in Figures A4 and A5. The differences are more pronounced and can be explained by significantly larger values of Mx and (FMx)−1.
Foam flow for Kref = 100 mD and Kz/Kx = 1, which is shown in Figure A6, also behaves similarly with more interlayer transfers due to the isotropic nature of the permeability which globally enhances the vertical sweep.
A last comparison is performed in Figure A7 where the impact of the typical layers thickness, Lz = 10 or 5 m, is shown for a scaled Mref with Mref,x = 500, Kref,x = 100 mD and Kz/Kx = 0.1. One can note a slightly better sweep for thinner layers such that Lz = 5 m which promote inter-layer vertical transfers.
Although we do not report in-situ profiles for every VDP values, it will be shown in Section 5 where production results are compared that the differences which have been observed for VDP = 0.75 gradually fade as VDP decreases. We will show further in Section 6 from production data that a VDP threshold exists from which this sweep improvement manifests itself significantly when scaling Mref.
4.3 Comparison of in-situ foam flow with and without Mref scaling: alternate injection
Let us now move on to foam flow where foam is formed in-situ by alternating surfactant solution and gas slugs, as indicated in Figure 1. Unlike the co-injection case described in the previous section, there is no quality control for the surfactant solution alternating gas injection as foam is formed by fingering of gas (injected after surfactant solution) through surfactant solution, or at least mixing of the two, due to their different mobility. The injected surfactant solution volume of 0.25 PV is the same as for the co-injection case. The behaviour of the pre-foam gas injection has been already commented in Section 4.1.
Figures A9, A10 and A11 compare the in-situ dynamic behaviour of foam flow (i) after 0.25 PV of surfactant solution injection (end of the surfactant solution injection), (ii) after 0.9 PV of gas injection (post surfactant solution injection), and (iii) after 1.8 PV of gas injection (post surfactant solution injection), without and with Mref scaling, for VDP = 0.75, Mref,x = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m.
There is a similar behaviour to co-injection with a very significant sweep improvement when scaling Mref, but with an additional period of time for the foam to form and lead to the same effects, which is expected for alternate injection and obviously depends on its design in terms of slug size. This can be seen very clearly by comparing Figures A2 and A9: while after 0.25 PV of surfactant solution injected the fluids diversion due to foam is clear for co-injection, it is hardly observed for the alternate injection. It is indeed necessary to wait until the following gas slug gives rise to the formation of foam. Regarding chemical additives, the main difference with co-injection is the less surfactant trapping in low-permeability layers. It should be noted that the remaining surfactant that can be observed in the central dominant layer in Figure A11 is not significant at all since it corresponds to very a very low water saturation tail that results from the poor displacement efficiency of gas injection. We will show further on by inspecting production results the differences that exist between alternate injection and co-injection, as there are. Let us quantify all this now in terms of the fluids produced by varying the degree of heterogeneity transcribed by VDP.
5 Comparison of foam flow production results with and without Mref scaling
We now explore the behaviour of the production results time evolution as a function of the Dykstra-Parsons coefficient over the range VDP = 0.22, …,0.75. Again, we compare the relative impact of the scaling of Mref with respect to simulations where Mref is constant. The analyzed production results are (i) NAPL recovery, expressed as the ratio of the cumulative volume of NAPL recovered over the initial volume of NAPL in place, (ii) produced surfactant concentration and cumulative mass, and (iii) produced cumulative gas volume.
The relative variations in these quantities are quantified in relation to (i) the twin chemicals-free injection type when scaling Mref or not (co-injection with chemicals is compared to co-injection without chemicals, and so on for alternate injection), and (ii) to a foam injection with a constant Mref when considering a scaled Mref (co-injection with Mref scaling is compared to co-injection without Mref scaling, and so on for alternate injection).
Although all the configurations reported in Table 3 were analyzed, it is sufficient to comment only the results obtained for Kref,x = 100 mD and either Mref,x = 500 or 1581 (or equivalently Mref,x = 500 and either Kref,x = 100 or 10 mD) and Kz/Kx = 0.1 within a co-injection (Sect. 5.1) or alternate injection (Sect. 5.2), for the sake of conciseness and readability. All the results of Table 3 configurations are presented in a more synthetic manner in Section 6.
5.1 Comparison of foam flow production results with and without Mref scaling: co-injection
To begin with, we note the extreme sensitivity of the NAPL recovery of a chemicals-free injection (in absence of foam) to the Dykstra-Parsons coefficient, as reported in Figure 5a: as VDP increases from 0.22 to 0.75, NAPL recovery approximately drops from 70% to 30%. The more heterogeneous the reservoir is (the higher VDP is), the smaller the vertical sweep of the reservoir by water or gas is (only the most permeable layers are swept). This behaviour is well known and has been studied in detail by numerous authors for water flooding [48–50].
Under foam flooding, results differences whether Mref is scaled or fixed are all the higher as the degree of heterogeneity, quantified byVDP, is higher. Thus the more heterogeneous the reservoir is, the smaller the vertical sweep of the reservoir by water or gas is, but the more efficient the foam is in its diversion role and the better the incremental vertical sweep and NAPL recovery are compared to a twin injection type without foam. The differences in NAPL recovery can reach about 20 and 10% during the transient regime, when scaling Mref with Mref,x = 500, Kref,x = 100 mD, for VDP = 0.72 and 0.75, respectively and relatively to a foam injection with a constant Mref, which is very significant. This is due to a better vertical sweep as explained in Section 4.2.
Also, we note a very strong impact on the surfactant breakthrough time and on the mass of surfactant recovered for VDP ≥ 0.57 when Mref is scaled with Mref,x = 500 and Kref,x = 100 mD, as reported in Figure 5b. The higher VDP is, the earlier the chemicals breakthrough and the larger the amount of recovered chemicals are for a constant Mref. This trend remains when scaling Mref but there is a significant delay in chemicals breakthrough and a reduction in recovered chemicals of about 20–40% for large VDP values (VDP ≥ 0.57) over constant Mref cases. Breakthrough time relative differences are quantified in Section 6. Again, this is due to a better vertical sweep that leads to additional trapping of surfactant in low-permeability layers, as explained in Section 4.2.
To finish with, the produced volume of gas is sensitive to VDP but much less than NAPL and surfactant recovery, as reported in Figure 6a. It is lowered by 5% for VDP = 0.75 when scaling Mref compared to a constant Mref. Such less contrasted behaviour is due to the high mobility of gas in the absence of foam generally speaking.
The behaviours observed for Mref,x = 1581 and Kref,x = 100 mD (or equivalently Mref,x = 500 and Kref,x = 10 mD) are similar and more pronounced when Mref is scaled compared to a constant Mref, as reported in Figures 6b, 7a and 7b, and as already observed from the in-situ profiles in Section 4.2. Let us give some orders of magnitude: when scaling Mref, transient NAPL recovery is improved by about 35% and 20% for VDP = 0.75 and 0.72, respectively, while chemicals production is lowered by about 50–60% for VDP ≥ 0.57. Gas production does not exhibit significant differences compared to the Mref,x = 500 mD and Kref,x = 100 mD case.
5.2 Comparison of foam flow production results with and without Mref scaling: Alternate injection
Let us come back the surfactant solution alternating gas injection. The same production results time evolution as previously is shown in Figures 8a and 8b for Mref,x = 500 and Kref,x = 100 mD, and in Figure 9 for Mref,x = 1581 and Kref,x = 100 mD (or equivalently Mref,x = 500 and Kref,x = 10 mD).
A critical dependence of NAPL recovery on VDP for a chemical-free injection is again noted: as VDP increases from 0.22 to 0.75, NAPL recovery drops from 70% to 20%, approximately. By scaling Mref it is improved by about 25%, 10% and 7% relatively to a constant Mref for VDP = 0.75, 0.72 and 0.66 when Mref,x = 500 and Kref = 100 mD, and by 40%, 23% and 10% relatively to a constant Mref for the same VDP values when Mref,x = 1581 and Kref = 100 mD. Again, the more heterogeneous the reservoir is (the higher VDP is), the smaller the vertical sweep of the reservoir by water or gas is, but the more efficient the foam is in its diversion role and the better the incremental vertical sweep and NAPL recovery are compared to a twin injection type without surfactant.
6 Sensitivity study on foam flow performance differential behaviour with and without Mref scaling
We now give a more global and synthetic view of the differentiated behaviour of foam flow performance by covering all the configurations reported in Table 3, 96 in number. To sum up:
-
Foam flow is considered through either co-injection of surfactant solution and gas or surfactant solution alternating gas injection. In both cases 0.25 PV of a 5000 ppm concentrated surfactant solution is injected as indicated in Figure 1. All foam flow simulations are performed at a constant total injection flow rate such that 1 PV of the reservoir is injected within one year.
-
A mobility reduction of Mref,x = 500 or 1581 is assigned to the reference horizontal permeability Kref,x = 100 mD that fits the average horizontal permeability 〈Kx〉. The case Mref,x = 1581 and Kref,x = 100 mD is equivalent to Mref,x = 500 and Kref,x = 10 mD that approximately corresponds to the low-permeability layers whenever the permeability map is heterogeneous enough.
-
The considered permeability map is such that Kz/Kx = 0.1 or 1.
-
Permeability maps of typical layers thickness of 10 m or 5 m are considered.
-
The Dykstra-Parsons coefficient that accounts for permeability heterogeneity
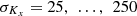 mD is set to VDP = 0.22, …, 0.75.
mD is set to VDP = 0.22, …, 0.75.
We now compare all the corresponding production indicators, NAPL recovery, chemicals and gas production, chemicals breakthrough time to identify trends. Specifically, special attention is paid to the thresholds in the Dykstra-Parsons coefficient, such that when scaling Mref significant differences are obtained due to a better vertical sweep, which is a consequence of flow diversion from most permeable layers by the play of the foam selective character, as previously reported in Sections 4 and 5.
Regarding NAPL recovery, we consider below the maximum variation in NAPL recovery during the transient regime under foam flooding while the cumulative mass of recovered chemicals and gas are taken at the end of Figure 1 injection sequences. All the reported production indicators variations when scaling Mref are relative to the same injection type, as in the previous sections, all things being equal except a constant Mref.
Figure 10a compares the maximum NAPL recovery relative variation when scaling Mref relatively to a constant Mref, as a function of the foam injection type (co-injection or alternate injection), VDP, Kref,x, Kz/Kx and Lz. Regardless of the configurations in the injection type, reference permeability, permeability anisotropy ratio, typical layers thickness, relative variation of NAPL recovery appears to approximately follow a power law of the Dykstra-Parsons coefficient, above some VDP threshold, as shown in Figure 10b in log-log scale.
This onset in the Dykstra-Parsons coefficient for activating additional inter-layer transfers is about VDP ∼ 0.6-0.7 for all cases, roughly speaking. NAPL recovery improvement can be as high as about 35% for the most heterogeneous case with VDP = 0.75. More precisely, this relative increase is about 20–35% in a co-injection mode for Kref,x = 100 or 10 mD, and of about 25–40% in an alternate injection mode for Kref,x = 100 or 10 mD, respectively.
The power law exponents reported in Figure 10b using a log-log scale approximately range from 8 to 13 and are close to 10 in terms of order of magnitude. The differential impact on NAPL recovery is very significant but less pronounced for thin layers with Lz = 5 m, as well as whenever permeability is isotropic with Kz/Kx = 1, which basically favors vertical flow.
The same comparison is reported in Figures 11a and 11b for the produced cumulative mass of chemicals and chemicals breakthrough time, respectively. No specific dependence on VDP is observed as for NAPL recovery. However, a VDP threshold (much less clear-cut than for NAPL recovery) about VDP ~ 0.6 emerges in all cases, such that for VDP ≥ 0.6 there is a significant (i) reduction of produced chemicals for co-injection up to 40–60% for Kref,x = 100 or 10 mD, and (ii) increase or little variation of produced chemicals for alternate injection, up to 5–12% for Kref,x = 100 or 10 mD.
Chemicals breakthrough time, shown in Figure 11b exhibits very significant delays for co-injection only and for VDP ≥ 0.5–0.6. It can be delayed up to 25–40% for Kref,x = 100 or 10 mD. No delay is noticeable for the alternate injection. Again, the impact of scaling Mref is still significant but less pronounced for thin layers with Lz = 5 m, as well as whenever permeability is isotropic with Kz/Kx = 1, which basically favors inter-layer transfers.
The differential behaviour of gas production is reported in Figure 12. There are very significant differences compared to the constant Mref cases as well, that mainly occur for VDP ≥ 0.7 for co-injection and lead to a reduction of gas production or an increase of it or little variation otherwise. There are little differences for the alternate injection, and the impact is again less pronounced for thin layers with Lz = 5 m, as well as whenever permeability is isotropic. Generally speaking, however, the relative variations of gas production are much less marked than for the previous indicators.
Figures 13 and 14 provide an overview of these results by distinguishing co-injection from alternate injection for each Dykstra-Parsons coefficient in order to quickly capture the key variations over the bundle of configurations of Table 3. A quick look will capture very significant variations for the most heterogeneous configurations for VDP > 0.6 and mainly for NAPL recovery and surfactant amounts produced.
7 Discussion
This work, as a follow-up of previous work [15, 52], tested a new scaling law that drives the maximum mobility reduction yielded by foam of Darcy-scale implicit-texture foam models as a function of the permeability of the reservoir rock. This scaling law for the effect of permeability on foam properties was inferred from an analogy between foam flow in porous media and foam flow in capillary tubes and was found consistent with the modelling of available experimental data.
We have shown step by step, by analyzing the in-situ saturation and composition profiles time evolution and the resulting production data, varying the degree of heterogeneity of a model stack-of-layers porous medium, how such a result, newly implemented in IFP Energies nouvelles reservoir simulator Puma, impacts the hydrodynamic behaviour of foam and causes, in the most heterogeneous cases, a flow diversion from high- to low-permeability layers that increases the vertical sweep.
A sensitivity study was carried out to account for foam injection type (co-injection of surfactant solution and gas or surfactant solution alternating gas injection), layers thickness, permeability anisotropy and, of course, the degree of heterogeneity of the reservoir transcribed by the Dykstra-Parsons coefficient.
The impact of this scaling law has been found moderate to very strong compared to simulations that do not account for it, according to the degree of reservoir heterogeneity. In a nutshell, the higher the heterogeneity is, the lower the sweep is but the higher the sweep improvement by foam is. Ignoring mobility reduction dependence on permeability in the foam process assessment of heterogeneous formations leads to an underestimation of mobility reduction benefits to improve flow conformance. As such, the question of cores selection is raised regarding foam evaluation in the laboratory and model calibration on selected rock types. Reservoir characterization remains more than ever a must.
NAPL relative incremental recovery, when scaling Mref, in relation to a constant Mref, has been found to follow a power-law behaviour as a function of the Dykstra-Parsons coefficient. The VDP thresholds above which these inter-layer transfers are effectively activated have been identified. Chemicals production is very significantly impacted as well.
Even though the porous medium considered in this work remains a two-dimensional toy model – it is however a deliberate choice in order to remain generic and moreover quite representative of the vertical sweep efficiency issue –, and given that the scaling law tested probably requires further verification and is not intended to apply to any rock type but rock type per rock type (there can very well be several regionalized Kref, Mref couples when considering multi-facies geological formations), it is clear, given the variability observed as a function of the scaling performed, that no Darcean simulation of foam flow in heterogeneous porous media can be taken seriously without substantial management of heterogeneity in relation to foam. This could be a decisive contribution to the predictivity of Darcy-type simulations for design purposes carried out prior to on-site tests, especially since investments are limited in the field of soil remediation. Good characterization of the considered porous medium and parameterization of the flow model, however imperfect and rustic it may be, are definitively unavoidable to achieve reliable predictions. In this respect, scaling laws, even approximate ones, should help guide smart and optimal sampling.
Surfactant adsorption and the impact of NAPL on foam, which were not taken into account in this work, should not significantly impact the observed trends. Indeed, the adsorption will have to be compensated by larger amounts of surfactant, and one can intuit that the anti-foaming impact of NAPL, initially redhibitory when considering foam as a frontal displacement fluid, may be secondary due to the placement of the foam in most permeable areas already desaturated from NAPL. A major issue not addressed in this work remains injectivity. Indeed, there is no guarantee in practice that foams developing relatively high apparent viscosities can inject and propagate in porous formations due to pressure constraints at injection and in the reservoir [40].
Another concern is about possible crossflow between close layers when gas is blocked in a high permeability layer. In this case gas flows in the low permeability layer but will be in contact with the high permeability layer and may be diverted towards the high permeability zone. This happens when the layers are in capillary contact and may be enhanced by buoyancy effect. The considered model porous medium, with a relatively low permeability, is not typical of subsurface aquifers commonly encountered with NAPL problems, and is likely to minimize gravity effects compared to classical subsurface aquifers.
To finish with, it is worth mentioning that the foam flow transient regime studied in this work with a steady-state mobility reduction implicit-texture model carries an ambiguity which remains to be clarified. The name, perhaps complicated on purpose, is indeed somewhat confusing, as this so-called steady-state model regarding foam actually accounts for the transient regime through the relative permeabilities interplay (the relative permeability to gas being modified in the presence of foam), like any standard Darcy-scale multiphase flow model. It seems to us that the ambiguity, let us say rather lack of validation, can only be resolved by means of well-controlled transient experiments, by minimizing the model adjustable parameters of which in practice they are numerous. A flawless characterization of three-phase flow relative permeabilities in the absence of foam is indeed required, possibly including hysteresis, as well as a thorough understanding and modelling of adsorption processes, devoid of any fudge factors. A certain research effort remains to be made in this area, apart from modelling.
Naturally fractured reservoirs with a poor recovery prognosis due to a preferential wettability to NAPL of the matrix rock are the most heterogeneous and present a similar problem to the one addressed in this work. Foam combines a reduction of fluid flow in the fracture network and the enhancement of fluids displacement in the matrix blocks thanks to the filtration of foam surfactant solution. Main expected effect is a forced two-phase displacement of the matrix NAPL by foam surfactant filtrate. A possible (but not guaranteed) additional benefit is the reduction of oil trapping through a modification of interfacial rock-fluids properties [20]. Needless to say, there is still room for improvement in dual-medium modelling that is necessary for performance purposes.
Notwithstanding, the authors hope that this work will contribute to a more reliable assessment of reservoir-scale foam processes, whether for soil remediation, carbon capture, utilization, and storage, or enhanced oil recovery, and that it will be followed up in the community to advance the knowledge of foams in heterogeneous porous media. The scaling trends reported in Table 1 [15] certainly remain to be further investigated as well as the subsequent examination of their exploitation in practice. Considerable progress also remains to be made to accurately predict the distances over which foam holds during its propagation in porous media, in relation to the transient mechanisms of destruction and generation that depend on the pore-scale structure of the porous medium. In this respect, it is perhaps not Darcy-type models that should be challenged first (population-balance models were made precisely for this purpose) but rather the characterization of the porous medium at the pore scale and its transcription to the Darcy scale. This may be an impossible task in terms of predictivity at the geological scale of interest and considering reduced pilot scales of the order of a hundred or fifty meters seems appropriate. One may wonder how much faster this science would progress if more proprietary data of multi-scale experiments were made public.
This layer-cake configuration is the most frequent and the simplest for sedimentary deposits [54]. In the context of this work, it is the minimum geological complexity needed in terms of permeability heterogeneity to highlight the selective behavior of foam in natural porous media.
This is known since the work of Leverett [55] for capillary pressure, 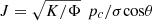 being invariant for a given rock-type (θ is the contact angle). Regarding adsorption, a basic calculation indicates rock adsorption capacity scales as
being invariant for a given rock-type (θ is the contact angle). Regarding adsorption, a basic calculation indicates rock adsorption capacity scales as 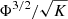 .
.
References
- Hirasaki G.J., Miller C.A., Szafranski R., Lawson J.B., Akiya N. (1997) Surfactant/foam process for aquifer remediation (Paper SPE 37 257), in: 1997 SPE International Symposium on Oilfield Chemistry, Houston, TX, USA, 18–21 February. [Google Scholar]
- Mamun C.K., Rong J.G., Kam S.I., Liljestrand H.M., Rossen W.R. (2002) Extending foam technology form improved oil recovery to environmantal remediation (Paper SPE 77557-MS), in: SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October. [Google Scholar]
- Atteia O., Del Campo Estrada E., Bertin H. (2013) Soil flushing: a review of the origin of efficiency variability, Rev. Environ. Sci. Biotechnol. 12, 379–389. [CrossRef] [Google Scholar]
- Bertin H., Del Campo Estrada E., Atteia O. (2017) Foam placement for soil remediation, Environ. Chem. 14, 338–343. [CrossRef] [Google Scholar]
- Karthick A., Roy B., Chattopadhyay P. (2019) A review on the application of chemical surfacant and surfacant foam for remediation of petroleum oil contaminated soil, J. Envoron. Manage. 243, 187–205. [CrossRef] [Google Scholar]
- Flaifel H., Izadi M., Park S., Gupta I., Lee G., Kam S.I. (2020) Shallow subsurface environmental remediation by using tracer-surfacant-foam processes: history-matching and performance prediction, Trans. Porous Media 134, 565–592. [CrossRef] [Google Scholar]
- Bouquet S., Douarche F., Roggero F., Leray S. (2020) Characterization of viscous fingering and channeling for the assessment of polymer-based heavy oil displacements, Trans. Porous Media 131, 873–906. [CrossRef] [Google Scholar]
- Puma is co-marketed by Beicip-Franlab and KAPPA Engineering, Available at https://www.beicip.com/reservoir-simulation and https://www.kappaeng.com/software/rubis-puma/overview. [Google Scholar]
- Bernard G., Jacobs W.L. (1965) Effect of foam on trapped gas saturation and on permeability of porous media to water, Soc. Pet. Eng. J. 5, 4, 295–300. [CrossRef] [Google Scholar]
- Lawson J.B., Reisberg J. (1980) Alternate slugs of gas and dilute surfactant for mobility control during chemical flooding (Paper SPE-8839-MS), in: SPE/DOE Enhanced Oil Recovery Symposium, Tulsa, Oklahoma, April. [Google Scholar]
- Friedmann F., Chen W.H., Gauglitz P.A. (1991) Experimental and simulation study of high-temperature foam displacement in porous media, SPE Res. Eng. 6, 1, 37–45. [CrossRef] [Google Scholar]
- Peaceman D.W. (1977) Fundamentals of numerical reservoir simulation, volume 6 of Developments in Petroleum Science, Elsevier Science, Amsterdam. [Google Scholar]
- Trangenstein J.A., Bell J.B. (1989) Mathematical structure of the black-oil model for petroleum reservoir simulation, SIAM J. Appl. Math. 49, 3, 749–783. [Google Scholar]
- Marle C.M. (1981) Multiphase flow in porous media, 3rd edn., Gulf Publishing Company. [Google Scholar]
- Gassara O., Douarche F., Braconnier B., Bourbiaux B. (2020) Calibrating and scaling semi-empirical foam flow models for the assessment of foam-based EOR processes (in heterogeneous reservoirs), Trans. Porous Media 131, 1, 193–221. [CrossRef] [MathSciNet] [Google Scholar]
- Gassara O., Douarche F., Braconnier B., Bourbiaux B. (2017) Calibrating and interpreting implicit-texture models of foam flow through porous media of different permeabilities, J. Pet. Sci. Eng. 159, 588–602. [Google Scholar]
- Gassara O., Douarche F., Braconnier B., Bourbiaux B. (2017) Equivalence between semi-empirical and population-balance foam models, Trans. Porous Media 120, 3, 473–493. [CrossRef] [MathSciNet] [Google Scholar]
- Weaire D., Hutzler S. (1999) The physics of foams, Oxford University Press. [Google Scholar]
- de Gennes P.-G., Brochard-Wyart F., Quéré D. (2004) Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer-Verlag. [CrossRef] [Google Scholar]
- Bouquet S., Douarche F., Roggero F., Bourbiaux B. (2020) Foam processes in naturally fractured carbonate oil-wet reservoirs: technical and economic analysis and optimization, J. Pet. Sci. Eng 190, 107111. [CrossRef] [Google Scholar]
- Aziz K., Settari A. (1985) Petroleum reservoir simulation, Elsevier. [Google Scholar]
- Fayers F.J. (1989) Extension of Stone’s method 1 and conditions for real characteristics in three-phase flow, SPE Res. Eng. 4, 4, 437–445. [CrossRef] [Google Scholar]
- Hirasaki G.J., Lawson J.B. (1985) Mechanisms of foam flow in porous media: apparent viscosity in smooth capillaries, SPE J. 25, 2, 176–190. [Google Scholar]
- Bretherton F.P. (1961) The motion of long bubbles in tubes, J. Fluid Mech. 10, 2, 166–188. [CrossRef] [MathSciNet] [Google Scholar]
- Ma K., Ren G., Mateen K., Morel D., Cordelier P. (2015) Modeling techniques for foam flow in porous media, SPE J. 20, 3, 453–470. [CrossRef] [Google Scholar]
- Ma K., Mateen K., Ren G., Luo H., Bourdarot G., Morel D. (2018) Mechanistic modeling of foam flow through porous media in the presence of oil: review of foam-oil interactions and an improved bubble population-balance model (Paper SPE 191 564), in: 2018 SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September. [Google Scholar]
- Chen Q., Kovscek A.R., Gerritsen M. (2010) Modeling foam displacement with the local-equilibrium approximation: theory and experimental verification, SPE J. 15, 1, 171–183. [CrossRef] [Google Scholar]
- Kovscek A.R., Radke C.J. (1994) Fundamentals of foam transport in porous media, in: M.J. Comstock, L.L. Schramm (eds), Foams: fundamentals and applications in the petroleum industry, American Chemical Society Advances in Chemistry. [Google Scholar]
- Patzek T.W. (1988) Description of foam flow in porous media by the population balance method, in: H.S. Duane (ed.), Surfactant-based mobility control, American Chemical Society Symposium Series, ACS, pp. 326–341, Available at https://pubs.acs.org/doi/pdf/10.1021/bk-1988-0373.ch016. [Google Scholar]
- Falls A.H., Hirasaki G.J., Patzek T.W., Gauglitz D.A., Miller D.D., Ratulowski T. (1988) Development of a mechanistic foam simulator: the population balance and generation by snap-off, SPE Reserv. Eng. 3, 3, 884–892. [CrossRef] [Google Scholar]
- Kam S.I., Nguyen Q.P., Li Q., Rossen W.R. (2007) Dynamic simulations with an improved model for foam generation, SPE J. 12, 1, 35–48. [CrossRef] [Google Scholar]
- Kam S.I. (2008) Improved mechanistic foam simulation with foam catastrophe theory, Colloids Surf. A Physicochem. Eng. Asp. 318, 1–3, 62–77. [CrossRef] [Google Scholar]
- Kovscek A.R., Bertin H.J. (2003) Foam mobility in heterogeneous porous media, Trans. Porous Media 52, 1, 37–49. [CrossRef] [Google Scholar]
- Farajzadeh R., Eftekhari A. (2017) Effect of foam on liquid phase mobility in porous media, Sci. Rep. 43870, 3011–3018. [Google Scholar]
- Farajzadeh R., Lotfollahi M., Eftekhari A.A., Rossen W.R., Hirasaki G.J.H. (2015) Effect of permeability on implicit-texture foam model parameters and the limiting capillary pressure, Energy Fuels 29, 5, 3011–3018. [Google Scholar]
- Khatib Z.I., Hirasaki G.J., Falls A.H. (1988) Effects of capillary pressure on coalescence and phase mobilities in foams flowing through porous media, SPE Res. Eng. 3, 3, 919–926. [CrossRef] [Google Scholar]
- Kapetas L., Vincent-Bonnieu S., Farajzadeh R., Eftekhari A.A., Mohd-Shafian S.R., Kamarul Bahrim R.Z., Rossen W.R. (2015) Effect of permeability on foam-model parameters – an integrated approach from coreflood experiments through to foam diversion calculations, in 18th European Improved Oil Recovery Symposium, Dresden, Germany, 14–16 April. [Google Scholar]
- Jian G., Zhang L., Da C., Puerto M., Johnston K.P., Biswal S.L., Hirasaki G.J. (2019) Evaluating the transport behavior of CO2 foam in the presence of crude oil under high-temperature and high-salinity conditions for carbonate reservoirs, Energy Fuels 33, 6038–6047. [CrossRef] [Google Scholar]
- Bergeron V., Radke C.J. (1992) Equilibrium measurements of oscillatory disjoining pressures in aqueous foam films, Langmuir 8, 12, 3020–3026. [CrossRef] [Google Scholar]
- Soulat A., Douarche F., Flauraud E. (2020) A modified well index to account for shear-thinning behavior in foam EOR simulation, J. Pet. Sci. Eng. 191, 107146. [CrossRef] [Google Scholar]
- Peaceman D. (1978) Interpretation of well-block pressures in numerical reservoir simulation, SPE J. 18, 3, 182–194. [Google Scholar]
- Batôt G., Delaplace P., Bourbiaux B., Pedroni L.G., Nabzar L., Douarche F., Chabert M. (2016) WAG management with foams: influence of injected gas properties and surfactant adsorption (Paper SPE 183 326), in: Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 7–10 November. [Google Scholar]
- Brooks R.H., Corey A.T. (1966) Properties of porous media affecting fluid flow, J. Irrig. Drain. Div. 92, 2, 61–88. [CrossRef] [Google Scholar]
- Standing M.B. (1974) Notes on relative permeability relationships, Technical report, Division of Petroleum Engineering and Applied Geophysics, Norwegian Institute of Technology, University of Trondheim. Available at https://blasingame.engr.tamu.edu/z_zCourse_Archive/P620_18C/P620_zReference/PDF_Txt_Std_Kr_Notes_(1973).pdf. [Google Scholar]
- de Figueiredo L., Grana D., Le Ravalec M. (2020) Revisited formulation and applications of FFT moving average, Math. Geosci. 52, 6, 810–816. [Google Scholar]
- Le Ravalec M., Nœtinger B., Hu L.Y. (2000) The fft moving average (FFT-MA) generator: an efficient numerical method for generating and conditioning Gaussian simulations, Mathe. Geol. 32, 6, 701–723. [CrossRef] [Google Scholar]
- Dykstra H., Parsons R.L. (1950) The prediction of oil recovery by waterflood, in: Secondary recovery of oil in the United States, American Petroleum Institute, Washington, DC, pp. 160–174. [Google Scholar]
- Craig F.F. (1993) The reservoir engineering aspects of waterflooding, volume 3 of SPE Monograph Series, Society of Petroleum Engineers. [Google Scholar]
- Willhite G.P. (1986) Waterflooding, volume 3 of SPE Textbook Series, Society of Petroleum Engineers. [Google Scholar]
- Lake L.W. (1989) Enhanced oil recovery, Prentice Hall. [Google Scholar]
- Green D.W., Willhite G.P. (1998) Enhanced oil recovery, volume 6 of SPE Textbook Series, Society of Petroleum Engineers. [Google Scholar]
- Douarche F., Braconnier B., Bourbiaux B. (2020) Scaling foam flow models in heterogeneous reservoirs for a better improvement of sweep efficiency (Paper ThB04), in: 17th European Conference of the Mathematics of Oil Recovery (ECMOR), Edinburgh, Scotland, 14–17 September. [Google Scholar]
- Pedroni L., Nabzar L. (2016) New insights on foam rheology in porous media, in: Rio Oil and Gas Expo and Conference Proceedings, Rio de Janeiro/Brazil, 24–27 October, (IBP. ISSN 2525 7560). [Google Scholar]
- Weber K.J., van Geuns L.C. (1990) Framework for constructing clastic reservoir simulation models, J. Pet. Technol. 42, 1248–1297. [CrossRef] [Google Scholar]
- Leverett M.C. (1941) Capillary behavior in porous solids (Paper SPE-941152-G), Trans. AIME 142, 152–169. [CrossRef] [Google Scholar]
Appendix
A.1 Estimation of Mref from measurements
We have indicated in Section 2.1 that Mref can be computed from the ratio of water-gas co-injection steady-state measurements of differential pressure across core-plugs, Δpf/Δp, with and without foam, as measured in the laboratory, given that Δp corresponds to a gas injection in the IT model according to (4). In fact it is not that simple, even assuming the reference injection leading to a stabilized steady-state Δp is a gas injection, in which case it would be tempting to consider that the ratio Δpf/Δp corresponds to Mref, where Δpf denotes the steady-state pressure drop obtained under a co-injection of surfactant solution and gas. Here is why and how to estimate Mref from such measurements. The point we wish to stress here is that the model Mref is generally larger than the measured Mref, which will be denoted Mlab hereafter. Moreover, in practice, it is common in the laboratory for reasons of convenience to compare the steady-state Δpf obtained under foam injection (most often co-injection of surfactant solution and gas at a prescribed quality close to the optimal one), not to the Δp obtained under the equivalent co-injection without surfactant, but to a water or gas injection. We illustrate that with a few examples and orders of magnitude.
Let us calculate the maximum mobility reduction Mref knowing the measured mobility reduction Mlab = Δpf/Δp where Δpf and Δp are respectively the steady-state pressure differences measured across core-plugs flooded by a surfactant solution/gas co-injection yielding foam and by the corresponding co-injection without surfactant, performed at the same quality fg (i.e. with the same volumes of injected water and gas). Darcy’s law, for foam flow and for the corresponding co-injection without surfactant, at the same imposed total flow rate and quality, writes for the gas phase (A1)where U is the total velocity. Indeed, not only the relative permeability to gas is modified in the presence of foam (
(A1)where U is the total velocity. Indeed, not only the relative permeability to gas is modified in the presence of foam (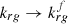 ), but the saturation of the displacing gas front is also (
), but the saturation of the displacing gas front is also (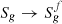 ). This is precisely what a Buckley-Leverett analytical calculation would predict [14]. From relations (A1) we get
). This is precisely what a Buckley-Leverett analytical calculation would predict [14]. From relations (A1) we get (A2)
(A2)
Moreover, in the presence of foam, we have (A3)according to (4). Under optimal reference conditions, FM given by (5) writes, using (A3)
(A3)according to (4). Under optimal reference conditions, FM given by (5) writes, using (A3)
 (A4)
i.e., using (A2)
(A4)
i.e., using (A2)
 (A5)
(A5)
The determination of Mref is thus reduced to that of the saturations 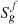 and
and  ,
, 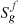 depending on Sg.
depending on Sg.
Determination of 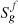 under foam injection. Darcy’s law, for foam flow and for the corresponding co-injection without surfactant, writes for the water phase
under foam injection. Darcy’s law, for foam flow and for the corresponding co-injection without surfactant, writes for the water phase (A6)
i.e. by forming the ratio
(A6)
i.e. by forming the ratio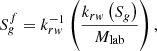 (A7)where
(A7)where 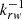 denotes the reciprocal of krw.
denotes the reciprocal of krw.
Determination of Sg under co-injection. The gas saturation Sg verifies the relation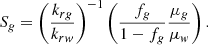 (A8)
(A8)
A similar calculation gives for a reference water injection (A9)and for a gas injection
(A9)and for a gas injection (A10)
(A10)
Orders of magnitude. Power-law relative permeabilities (16) and (17) rewrite for a water and gas two-phase flow in the absence of NAPL, setting Sorw = Sorg (A11)with SG = (Sg − Sgr)/(1 − Swi − Sgr). Having measured Mlab, to determine Mref we compute Sg according to (A8), then
(A11)with SG = (Sg − Sgr)/(1 − Swi − Sgr). Having measured Mlab, to determine Mref we compute Sg according to (A8), then  following (A7) and finally Mref from (A5). Some examples are given in Table A1. The Mref values of 500 and 1581 assigned to Kref = 100 mD in this work correspond to Mlab = 71 and 196 if the reference injection is a co-injection of water ans gas, and to Mlab = 272 and 746 if the reference injection is water flooding, respectively. These are quite reasonable values that are not abnormally large at all. They are even relatively low compared to what is generally measured [15, 35, 53].
following (A7) and finally Mref from (A5). Some examples are given in Table A1. The Mref values of 500 and 1581 assigned to Kref = 100 mD in this work correspond to Mlab = 71 and 196 if the reference injection is a co-injection of water ans gas, and to Mlab = 272 and 746 if the reference injection is water flooding, respectively. These are quite reasonable values that are not abnormally large at all. They are even relatively low compared to what is generally measured [15, 35, 53].
Examples of Mlab to Mref conversion for a reference injection which is eiher a co-injection of water and gas or a water injection (the gas considered is CO2 with T = 100 °C and p = 100 bar).
A.2 Comparison of in-situ profiles with and without Mref scaling
 |
Fig. A1 Co-injection case after 1 PV of water injection prior to surfactant solution/gas co-injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x . Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A2 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A3 Co-injection case final state, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A4 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 1581, Kref,x = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A5 Co-injection case final state, with Mref,x = 1581, Kref,x = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A6 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A7 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75 and Lz = 10 m. Left: scaled Mref,x with Kz/Kx = 1. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x with Kz/Kx = 0.1. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling (“ani” and “iso” stand for Kz/Kx = 0.1 and 1, respectively). |
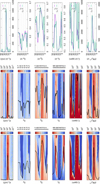 |
Fig. A8 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75 and Kz/Kx = 0.1. Left: scaled Mref,x with Lz = 10 m. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x with Lz = 5 m. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling (“Lz” and “Lz/2” stand for Lz = 10 and 5 m, respectively). |
 |
Fig. A9 Alternate injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, and Kz/Kx =0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A10 Alternate injection case post surfactant solution injection after approximately 0.9 PV of gas injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
 |
Fig. A11 Alternate injection case post surfactant solution injection after approximately 1.8 PV of gas injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
All Tables
Examples of Mlab to Mref conversion for a reference injection which is eiher a co-injection of water and gas or a water injection (the gas considered is CO2 with T = 100 °C and p = 100 bar).
All Figures
 |
Fig. 1 Timeline of surfactant solution/gas co-injection (blue) and surfactant solution alternating gas injection (red) scenarios, where W, G and W* denote water, gas and surfactant solution, respectively. Timescale is indicated in injected pore volumes (PV, volume of fluid injected over the pore volume of the porous medium). Both cases have a pre-foam water or gas injection history of 1 PV. In each case the volume of surfactant solution injected of 0.25 PV is identical: in the co-injection case, it is distributed over a total volume of gas and surfactant solution of 1.25 PV according to the imposed quality of fg = 0.8 that corresponds to optimal foaming conditions. There is no such quality control for the surfactant solution alternating gas injection, where foam is formed by fingering of gas (injected after surfactant solution) through surfactant solution, or at least mixing of the two, due to the different mobility of the fluids. |
| In the text | |
 |
Fig. 2 Water/NAPL and gas/NAPL two-phase subsystems power-law relative permeabilities and capillary pressures (16) and (17) with parameters given in Table 2. |
| In the text | |
 |
Fig. 3 Comparison of several two-dimensional horizontal permeability field Kx(x, z) realizations (approximately log-normal distributed) with constant mean 〈Kx〉 = 100 mD and standard deviation |
| In the text | |
 |
Fig. 4 Comparison of several two-dimensional horizontal permeability field Kx(x, z) realizations (approximately log-normal distributed) with constant mean 〈Kx〉 = 100 mD and standard deviation |
| In the text | |
 |
Fig. 5 Co-injection case with Mref,x = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
| In the text | |
 |
Fig. 6 Co-injection case with Kref,x = 100 mD, (a) Mref,x = 500, (b) Mref,x = 1581 (or equivalently Mref,x = 500, (a) Kref,x = 100 mD, (b) Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of produced cumulative gas volume (Vg) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
| In the text | |
 |
Fig. 7 Co-injection case with Mref,x = 1581, Kref = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
| In the text | |
 |
Fig. 8 Alternate injection case with Mref,x = 500, Kref,x = 100 mD, Kz/Kx = 0.1 and Lz = 10 m. Comparison of (a) NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) and (b) produced surfactant concentration (Cf) and cumulative mass (Mf) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
| In the text | |
 |
Fig. 9 Alternate injection case with Mref,x = 1581, Kref,x= 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), Kz/Kx = 0.1 and Lz = 10 m. Comparison of NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) time evolution as a function of VDP for chemicals-free injection (“nofoam”), foam with constant Mref,x (“ref”, dashed lines) and scaled Mref,x (“mod”, solid lines). Relative variations are either in relation to a chemicals-free twin injection (“/ nofoam”) or a constant Mref,x case (“/ foam”). |
| In the text | |
 |
Fig. 10 Comparison of the maximum NAPL recovery factor (RF, produced NAPL volume over initial NAPL volume in place, OOIP) relative variation under foam flooding with scaled Mref,x relatively to constant Mref, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
| In the text | |
 |
Fig. 11 Comparison of the (a) final produced surfactant cumulative mass (Mf) and (b) chemicals breakthrough time (BT) relative variation under foam flooding with scaled Mref,x relatively to constant Mref,x, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
| In the text | |
 |
Fig. 12 Comparison of the produced cumulative gas volume (Vg) relative variation under foam flooding with scaled Mref,x relatively constant Mref,x, as a function of the injection sequence (co-injection or alternate injection), VDP, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz. |
| In the text | |
 |
Fig. 13 Comparison of the differential behaviour of production results under foam flooding with scaled Mref,x relatively to constant Mref,x as a function of the injection sequence (co-injection or alternate injection), VDP = 0.22, 0.37, 0.57, Kref,x = 100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz (subscripts “ani” and “iso” stand for Kz/Kx = 0.1 and 1 while “Lz” and “Lz/2” correspond to Lz = 10 and 5 m, respectively). |
| In the text | |
 |
Fig. 14 Comparison of the differential behaviour of production results under foam flooding with scaled Mref,x relatively to constant Mref,x as a function of the injection sequence (co-injection or alternate injection), VDP = 0.66, 0.72, 0.75, Kref,x =100, 10 mD assigned to Mref,x = 500 (or equivalently Mref,x = 500, 1581 assigned to Kref,x = 100 mD), Kz/Kx and Lz (subscripts “ani” and “iso” stand for Kz/Kx = 0.1 and 1 while “Lz” and “Lz/2” correspond to Lz = 10 and 5 m, respectively). |
| In the text | |
 |
Fig. A1 Co-injection case after 1 PV of water injection prior to surfactant solution/gas co-injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x . Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A2 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A3 Co-injection case final state, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A4 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 1581, Kref,x = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A5 Co-injection case final state, with Mref,x = 1581, Kref,x = 100 mD (or equivalently Mref,x = 500, Kref,x = 10 mD), VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A6 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A7 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75 and Lz = 10 m. Left: scaled Mref,x with Kz/Kx = 1. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x with Kz/Kx = 0.1. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling (“ani” and “iso” stand for Kz/Kx = 0.1 and 1, respectively). |
| In the text | |
 |
Fig. A8 Co-injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75 and Kz/Kx = 0.1. Left: scaled Mref,x with Lz = 10 m. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x with Lz = 5 m. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling (“Lz” and “Lz/2” stand for Lz = 10 and 5 m, respectively). |
| In the text | |
 |
Fig. A9 Alternate injection case after 0.25 PV of surfactant solution injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, and Kz/Kx =0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A10 Alternate injection case post surfactant solution injection after approximately 0.9 PV of gas injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
 |
Fig. A11 Alternate injection case post surfactant solution injection after approximately 1.8 PV of gas injection, with Mref,x = 500, Kref,x = 100 mD, VDP = 0.75, Kz/Kx = 0.1 and Lz = 10 m. Left: constant Mref,x. Solid and dashed lines stand for horizontally and vertically averaged profiles, respectively. Center: scaled Mref,x. Right: comparison of horizontally averaged profiles without (“ref”) and with (“mod”) Mref,x scaling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.