4E Analysis of solar photovoltaic, wind, and hybrid power systems in southern Pakistan: energy, exergy, economic, and environmental perspectives | Science and Technology for Energy Transition (STET)

Open Access

Table 4

Methods for calculating the Weibull parameters.

Method	Formulation
Method	Shape Factor (k)	Scale Factor (c)
Least Square Method	$\frac{\begin{matrix} N \sum_{i = 1}^{N} \ln v_{i} \times \ln [- \ln {1 - F (ν)}] \\ \times \sum_{i = 1}^{N} \ln v_{i} \sum_{i = 1}^{N} \ln [- \ln {1 - F (ν)}] \end{matrix}}{N \sum_{i = 1}^{N} \ln v_{i}^{2} - {(\sum_{i = 1}^{N} \ln v_{i})}^{2}}$ $\frac{\begin{array}{c}N\sum_{i=1}^N\mathrm{ln}{v}_i\times \mathrm{ln}\left[-\mathrm{ln}\left\{1-F\left(\nu \right)\right\}\right]\\ \times \sum_{i=1}^N\mathrm{ln}{v}_i\sum_{i=1}^N\mathrm{ln}\left[-\mathrm{ln}\left\{1-F\left(\nu \right)\right\}\right]\end{array}}{N\sum_{i=1}^N\mathrm{ln}{v}_i^2-{\left(\sum_{i=1}^N\mathrm{ln}{v}_i\right)}^2}$	$\exp [\frac{k \sum_{i = 1}^{N} \ln ν - \sum_{i = 1}^{N} \ln [- \ln 1 - F (v)]}{Nk}]$ ${exp}\left[\frac{k\sum_{i=1}^N\mathrm{ln}\nu -\sum_{i=1}^N\mathrm{ln}\left[-\mathrm{ln}1-F(v)\right]}{{Nk}}\right]$
Maximum Likelihood Method	${[\frac{\sum_{i = 1}^{N} ν_{i}^{k} \ln (ν_{i}) f (ν_{i})}{\sum_{i = 1}^{N} ν_{i}^{k} f (ν_{i})} - \frac{\sum_{i = 1}^{N} \ln (ν_{i}) f (ν_{i})}{f (ν \geq 0)}]}^{- 1}$ ${\left[\frac{\sum_{i=1}^N{\nu }_i^k\mathrm{ln}\left({\nu }_i\right)f\left({\nu }_i\right)}{\sum_{i=1}^N{\nu }_i^k\hspace{0.25em}f\left({\nu }_i\right)}-\frac{\sum_{i=1}^N\mathrm{ln}\left({\nu }_i\right)f\left({\nu }_i\right)}{f\left(\nu \ge 0\right)}\right]}^{-1}$	${[\frac{1}{f \geq 0} \sum_{i = 1}^{N} ν_{i}^{k} f (ν_{i})]}^{\frac{1}{k}}$ ${\left[\frac{1}{f\ge 0}\sum_{i=1}^N{\nu }_i^kf\left({\nu }_i\right)\right]}^{\frac{1}{k}}$
Empirical Method of Lysen	${(\frac{σ_{std}}{\bar{v}})}^{- 1.086}$ ${\left(\frac{{\sigma }_{\mathrm{std}}}{\bar{v}}\right)}^{-1.086}$	$\bar{v} {(0.568 + \frac{0.433}{k})}^{- \frac{1}{k}}$ $\bar{v}{\left(0.568+\frac{0.433}{k}\right)}^{-\frac{1}{k}}$
Empirical Method of Justus	${(\frac{σ_{std}}{\bar{v}})}^{- 1.086}$ ${\left(\frac{{\sigma }_{\mathrm{std}}}{\bar{v}}\right)}^{-1.086}$	$\frac{\bar{v}}{Γ (1 + 1 / k)}$ $\frac{\bar{v}}{\Gamma \left(1+1/k\right)}$
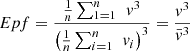
Energy Pattern Factor Method	$(1 + \frac{3.69}{{Epf}^{2}})$ $\left(1+\frac{3.69}{{{Epf}}^2}\right)$ where $Epf = \frac{\frac{1}{n} \sum_{1 = 1}^{n} v^{3}}{{(\frac{1}{n} \sum_{i = 1}^{n} v_{i})}^{3}} = \frac{v^{3}}{{\bar{v}}^{3}}$ ${Epf}=\frac{\frac{1}{n}\sum_{1=1}^n\enspace {v}^3}{{\left(\frac{1}{n}\sum_{i=1}^n\enspace {v}_i\right)}^3}=\frac{{v}^3}{{\bar{v}}^3}$	$\frac{\bar{v}}{Γ (1 + 1 / k)}$ $\frac{\bar{v}}{\Gamma \left(1+1/k\right)}$

Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.

Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.

Le chargement des statistiques peut être long.