Open Access
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.





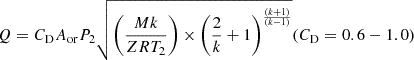
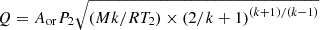
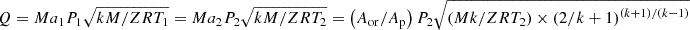
![$ Q={A}_{\mathrm{h}}{C}_{\mathrm{D}}{M}_3\sqrt{k{\rho }_{2\mathrm{t}}{P}_{2\mathrm{t}}{\left[2/\left(\left(k-1\right){M}_3^2+2\right)\right]}^{\left(k+1\right)/\left(k-1\right)}}$](/articles/stet/full_html/2025/01/stet20250123/stet20250123-eq21.gif)