EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 79 (2024) Sci. Tech. Energ. Transition, 79 (2024) 34 Full HTML
Open Access

This article has an erratum: [https://doi.org/10.2516/stet/2024074]

Issue
Sci. Tech. Energ. Transition
Volume 79, 2024
Article Number 34
Number of page(s) 15
DOI https://doi.org/10.2516/stet/2024028
Published online 11 June 2024

© The Author(s), published by EDP Sciences, 2024

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Reactive flow within porous media is a critical phenomenon exerting significant influence on a diverse array of geological and chemical processes, as well as engineering applications [1]. It lies at the core of comprehending processes such as diagenesis [2–4], karstification [5–7], geologic sequestration of carbon dioxide [8–11], contaminant transport in groundwater resources [12–14], safe disposal of nuclear waste [15], and the acidizing treatment of reservoir [16–18]. To investigate the reaction-dissolution mechanism of acid in porous media, researchers have conducted numerous experimental studies [19–23]. The results of the core acidization experiments show that the dissolution pattern resulting from acid-rock dissolution correlates with parameters such as the type of acid, core size, and injection rate. Nonetheless, reproducing the intricate environments and multifaceted influences encountered in actual reservoirs presents challenges in laboratory experiments. Hence, researchers frequently turn to numerical simulations to delve deeper into reactive flow processes.

Numerical simulations encompass various influencing factors and intricate geological conditions, thereby furnishing forecasts and interpretations of observed phenomena and behaviors in actual reservoirs [18, 24–37]. In numerical simulations of various reaction flows, reactions can be classified based on reaction kinetics into irreversible reactions and reversible reactions. For instance, the reaction of hydrochloric acid with carbonate rocks [38, 39] is considered an irreversible reaction, while the reaction of carbon dioxide solution with rocks [40–42] is classified as a reversible reaction. Additionally, there exist multi-step reactions, such as the flow reaction of hydrofluoric acid in sandstone [43–45]. Among these, reactive flows in carbonatite media are valued for their extensive applications across multiple fields [10, 46, 47].

To investigate the dynamics of hydrochloric acid dissolution in carbonate rocks, Panga et al. [25] developed a two-scale continuum (TSC) model. This model delineated the flow and transport of acid at the Darcy scale while characterizing the dynamic alterations of pore-scale parameters through empirical formulations. Subsequently, Kalia et al. [48] examined the influence of media heterogeneity on wormholes utilizing this model. It was observed that heterogeneity within a rock not only influences the structure of patterns formed during reactive dissolution but also affects the quantity of acid required to achieve a specific increase in permeability. Recognizing the significant impact of heterogeneity on the dissolution dynamics of acidic rocks, researchers began exploring the effects of larger-scale heterogeneity, such as the presence of fractures and vugs, on the reaction process and dissolution outcomes. Izgec et al. [49] examined the characteristics of vuggy carbonate rocks during reactive flow through experiments and numerical simulations. Chen et al. [50] and Khoei et al. [51], respectively, solved the fractured medium reaction flow model based on the unified pipe-network method and the finite element method. Huang et al. [52] treated vugs as anomalous matrices with high porosity, employing COMSOL software to solve the reaction flow model and investigate the influence of vug presence on wormhole growth and development structure. Liu et al. [53] tailored for fractured carbonate reservoirs, integrating concepts from the discrete fracture model and the TSC model. Utilizing the finite volume approach, the model effectively examined the impact of fracture characteristic parameters on wormhole formation. Qi et al. [54] regarded fractures as matrices with specific high porosity and utilized COMSOL software to explore the influence of fracture geometry on the initiation and propagation of wormholes. Through parameter sensitivity analysis, Jia et al. [55] examined the reaction flow processes of two typical core scales of vugular carbonate rocks as well as isolated vug carbonate rocks. They found that the vug filling degrees and vug diameter all had a significant effect on the reactive flow of fluids in carbonate rocks. Asl et al. [56] simulated the reaction flow process by combining the pseudofracture approach with the TSC model, wherein Darcy’s law governed the flow within the matrix and vugs, while the cubic law mimicked the flow within the fractures. They elucidated the impacts of individual fractures and vugs and analyzed the effects of various arrangements of fractures and vugs on reactive flow. Wang et al. [57] devised a statistical model of natural fractures employing the Monte Carlo method. This model integrates the matrix porosity model, fracture distribution model, and TSC model to simulate the formation mechanism of wormholes in naturally fractured reservoirs under radial flow conditions. Liu et al. [58] extended the TSC model to encompass fracture-vuggy porous media. They solved the model under both linear and radial conditions in three dimensions and conducted sensitivity analysis on the parameters associated with vugs and fractures.

In specific domains of geoengineering, non-Newtonian fluid acids find application in injection operations. For instance, in geothermal reservoir acidization, gelled acid is frequently employed to moderate the reaction rate owing to the reservoir’s elevated temperature. Investigating the reactive flow of such non-Newtonian acid types in carbonatite media, Ratnakar et al. [59] utilized the TSC model in conjunction with an empirical rheological model to elucidate the reactive transport of gelled acids on the Darcy scale. Their study explored the impact of rheological parameters on dissolution phenomena. Similarly, Maheshwari et al. [60] examined the three-dimensional reactive dissolution of gelled acid utilizing the two-scale continuum model, with a specific focus on the implications of non-Newtonian behavior on wormhole propagation. Liu et al. [61] introduced a coupled Thermal-Hydrological-Chemical (T-H-C) model to delineate the acidization dissolution of carbonate rock using gelled acid. This model scrutinized the dynamics of polymer adsorption, temperature variations, and the non-Newtonian behavior of the introduced acid. However, prevailing research on the reactive flow of gelled acid predominantly concentrates on the rock without field-scale heterogeneities. Given that carbonate reservoirs commonly encompass fractures and vugs, the significance of these geological structures in the reactive flow process cannot be overstated. To enhance the fidelity of reactive flow simulations in real formations, it is imperative to consider the effects of fractures and vugs, thereby facilitating a comprehensive evaluation of the mechanism underlying wormhole formation induced by gelled acid.

This study extends the T-H-C coupled model established by Liu et al. [62] to encompass fracture-vuggy porous media. Vugs are characterized as matrix clusters with significantly elevated porosity, as described by Liu et al. [58], while fractures are delineated using the pseudo-fracture model [63]. For computational simplification, the matrix, vugs, and fractures are all discretized within the same grid system.

The paper is structured as follows: Section 2 presents the development of a comprehensive mathematical model to describe the reaction flow behavior of gelled acid in carbonate fracture-vuggy systems. The alterations in the in situ viscosity of the gelled acid are elucidated using a rheological model. In Section 3, the model from Section 2 is rendered in a dimensionless form. Section 4 outlines the numerical algorithm utilized for solving the model. Section 5 conducts pertinent numerical simulations aimed at scrutinizing the influence of rheological behavior, fractures, and vugs on the reaction flow process. Finally, Section 6 summarizes the paramount findings of this study.

2 Mathematical model

2.1 Rheological model

Gelled acids exhibit non-Newtonian fluid behavior, which differs from the flow properties of Newtonian fluids [60]. The whole rheological model, which takes into account temperature, shear-thinning behavior, and polymer concentration, shows how the in situ viscosity changes [61]. It is written as(1)where μsitu represents the viscosity of gelled acid; μHCl indicates the concentration of pure HCl; μ0 is the gelled acid’s zero shear viscosity at temperature T0 and polymer concentration cp0; and K is the porous media’s effective permeability. The constant ξ is affected by the fluid’s properties.

2.2 Reaction transport model

This subsection mainly describes heat transfer, injected acid flow in fracture-vuggy carbonate rocks, changes in rock porosity in porous media, and species transport [64, 65]

The equations are expressed as follows:(2)where μsitu and u, respectively, represent the viscosity and velocity of the gelled acid; t denotes the time; ϕ signifies the porous media’s porosity; K stands for the porous media’s permeability; ch denotes the hydrogen ions cup-mixing concentrations; cp denotes the cup-mixing concentrations of polymers; av is the specific surface area; kc defines the local mass-transfer coefficient; ks is the constant for the surface reaction rate.; Dep and De are efficient dispersion tensors for polymers and hydrogen ions, respectively; and stand for the specific heat capacities of the gelled acid and the rock, respectively; and are the thermal conductivities of the gelled acid and the rock, respectively; ρl and ρr are the densities of the gelled acid and the rock, respectively; and ΔHr(T) signifies the temperature-dependent exothermic heat of the reaction per mole of hydrogen ions consumed.

2.3 Pore-scale model

For the reaction transport model, some physical parameters such as pore-specific surface area, permeability, the local mass-transfer coefficient, and pore radius are required. However, these parameters undergo changes due to the dissolution reaction, which constantly alters the porous media’s pore structure. To determine these parameters, the porescale model [64] can be employed to calculate their values using empirical equations. Subsequently, these parameters are applied in reaction transport model to describe transport and fluid flow behavior in porous media.

The pore-scale equation is expressed as follows:(3) (4) (5) (6) (7) (8)where ϕ0, K0, r0, and a0 denote initial porosity, initial permeability, initial pore radius, and initial specific surface area, respectively; The pore radius is rp; Df refers to the fractal dimensions of pore space; DT refers to the fractal dimensions of tortuosity; dE denotes the Euclidean dimension, which is assigned a value 2 for a two-dimensional space. The smallest and greatest pore diameters are represented by λmin and λmax, respectively. Sh∞ indicates asymptotic Sherwood number; Rep indicates pore Reynolds number; Sc indicates Schmidt number; |u| indicates the magnitude of Darcy’s velocity; DeL denotes the diffusion coefficient in the acid injection’s direction; DeT denotes the diffusion coefficient in the direction perpendicular to the acid injection direction; αos, λL, and λT are pore structure-related constants.

2.4 Initial and boundary conditions

The gelled acid is introduced continuously at a constant velocity from the inlet, with the outlet pressure being consistently maintained at a predetermined value.

In terms of fluid flow, the subsequent conditions are applicable:(9)

Pe is a representation of the outlet boundary’s fixed pressure.

Regarding the transport of polymers and hydrogen ions, the boundary conditions are as follows:(10)where ch0 and cp0 are the inlet hydrogen ions and polymer concentrations; u0 is the constant injection rate.

For heat transfer,(11)where Tf is the temperature at which the acid is injected.

For the transverse boundaries in the context of linear flow cases, the imposition of no-flux conditions serves to confine fluid, solute, and heat within the domain.(12)

Periodic boundary conditions are applied across transverse boundaries in the case of radial flow in order to regulate solute transport, fluid flow, and heat transfer, mirroring the following:(13)

The initial conditions for the system are defined as follows:(14)

For fracture-vuggy carbonate formations, the establishment of the spatial arrangement encompassing pores, fractures, and vugs is mainly divided into three parts:

  • 1.

    Establishing a random porosity field [62].

  • 2.

    For the realization of fracture generation and simulation. First, we simulate the distribution characteristics of porosity in the formation by using the initial porosity field with specific correlation length and heterogeneity constructed in step 1. Then, create a random fracture model in two-dimensional space using random numbers to determine the central location, orientation, length, and aperture of fractures [58, 63]. These fractures are represented as line segments. We deal with fractures beyond the physical area using the circular window [58] perimeter clipping approach, which allows simulation to adapt to radial flow conditions. The fracture grid is recognized during the numerical simulation stage by looking to see if the edge of each grid cell intersects the fracture. The adjacent grid crossing that edge is designated as a fractured grid if a grid cell’s boundary crosses a fracture. Finally, high porosity values are assigned to these grids to reflect the permeability of the fractures. The permeability of fracture grid is calculated by the formula Kfr = b 2/12. b is the fracture aperture, whose value is 1 mm in simulation. The calculated fracture permeability is 8 × 107 md. The porosity of the fracture grid is calculated by equation (15) where the average porosity is 0.35 and the average permeability is 0.1 md, which means that the fracture porosity is 0.99.

(15)
  • 3.

    During the process of constructing a vug distribution model, regions in the porosity field with porosity exceeding the average porosity are first identified and designated as vug units [58]. Subsequently, the index positions of these vug units within the grid are determined, and their porosity values are adjusted accordingly. The porosity of the vug areas is set within the range between the average matrix porosity to 1. In this study, we have set the porosity of the vug units to 0.99 and mapped them onto the porosity field. By adjusting the spatial correlation length and heterogeneity coefficient, we are able to generate random vug models with varying densities, volumes, and connectivity.

3 Dimensionless model

The following dimensionless parameters are defined.where the subscript letter D indicates dimensionless; For radial flow conditions, L symbolizes the characteristic length along the flow direction, corresponding to the core radius under radial flow conditions; U represents the dimensionless velocity; ka refers to the dimensionless effective permeability; is the Thiele modulus at the pore scale; η signifies the pore-to-domain scale ratio; AE denotes the dimensionless activation energy; and HD stands for the dimensionless reaction exothermic.

The following non-dimensional form can be obtained to express the mathematical model mentioned above.(16) (17) (18) (19) (20) (21) (22) (23) (24)

Boundary and initial conditions:(25) (26) (27) (28) (29) (30)

4 Numerical methods

The equations (16)–(21) are decoupled and solved using the sequential method for simulation of the injection of gelled acid through the rock. The following steps outline the simulation process:

  1. Determine the initial values: Use the hydrogen ions, polymer concentration, temperature, porosity, and velocity field at time t0 as initial values.

  2. Solve the flow equations (16) and (17) to compute the velocity U n+1 at t + Δt.

  3. Substituting U n+1 into the species equations (18) and (19), along with the heat transfer equation (20), couple them with the dissolution equation (21) to determine the distributions of hydrogen ions, polymer concentration, temperature, and porosity at t + Δt.

  4. Using the obtained solutions, update the pore-scale parameters.

  5. Shift from time n + 1 (i.e., t + Δt) back to time n (i.e., t).

  6. Return to step 2 and repeat the process until the injected acid breakthrough occurs.

In brief, the process involves solving the species and heat transfer equations from initial values and flow equations. The process of injecting gelled acid through rock is simulated by continuously updating the pore-scale parameters and repeating the solution.

Since the gelled acid’s in situ viscosity is a nonlinear function of the Darcy velocity, iterations are performed to obtain an accurate solution. In each iteration, the current viscosity value is substituted into equations (16) and (17) to solve for the velocity. The obtained velocity is then used in the viscosity equation (1) to calculate the new viscosity value. This process of iteration persists until convergence is attained.

For the calculation of polymer, hydrogen ions concentration, and temperature distribution, the reaction-transport process is decoupled using the operator splitting method. For a more detailed description of the solution process, interested readers may refer to [61].

5 Simulation results and analysis

In real reservoir acidizing operation, acid flow is radial. Therefore, we adopted the numerical simulation under the condition of two-dimensional radial flow. The corresponding simulation results are given in this section. Table 1 provides a list of the simulation’s input parameters. Unless otherwise stated, all parameters remained unchanged throughout the research.

Table 1

List of parameter values for the simulation

5.1 Dissolution modes by accordance with various injection rates

Wormhole growth and development in high-temperature carbonate rocks are significantly influenced by the rate of acid injection. Therefore, in this study, the dissolution effects of HCl and gelled acid at different injection rates were compared at 375 K. In the simulation, the initial porosity distribution of all cores is consistent. The simulation conditions are set as follows: fractures are 10, the length is 2 R/6, the average orientation is 60°, and the standard deviation of the orientation is 20°. Set the associated length of the vug to lx = ly = 0.09. Other parameters remain unchanged, as shown in Figure 1, where Figure 1a represents the initial fracture-vuggy structure, and Figures 1b–1f show the dissolution mode formed under different injection speeds, and each letter corresponds to the same injection speed value.

thumbnail Fig. 1

The dissolution modes of HCl and gelled acid were compared at different injection rates at 375 K. (A) HC1 (B) Gelled acid (a) initial fracture-vuggy structure, (b) 1/Da = 10−6, (c) 1/Da = 10−5, (d) 1/Da = 10−4, (e) 1/Da = 10−3, (f) 1/Da = 1.

Through comparative analysis, we can see that under a high-temperature environment, compared with HCl, gelled acid can form wormhole dissolution mode at a lower injection rate, and its dissolution range is wider. At the same injection rate, the wormhole formed of gelled acid has stronger breathability, a larger coverage area of the wormhole, and a better dissolution effect. In addition, from the breakthrough volume data required for injected acid to break through the core (Fig. 2), the amount required for gelled acid under the same conditions is less than the amount of HCl. This indicates that gelled acid not only has high dissolution efficiency under high-temperature conditions but also has less dosage.

thumbnail Fig. 2

The breakthrough volume required for HCl and gelled acid injection under different injection rate conditions.

In summary, in the acidization treatment of high-temperature carbonate rocks, gelled acid shows more obvious advantages compared with HCl because of its lower amount required for acidization and more uniform dissolution effect.

5.2 Effect of rheological properties on wormhole propagation

The properties of gelled acid are affected by rheological parameters. According to equation (1), rheological property is related to power-law index. The characteristics of fluid viscosity with shear rate are described by the power-law index. There is a power law relationship between the fluid’s viscosity and shear rate. This section uses the power-law index to examine how rheological characteristics affect wormhole propagation.

5.2.1 Power-law index

In this subsection, we analyze the power-law index’s impact on the dissolution dynamics. The power-law index, denoted by n, is varied as n = 0.1, 0.3, 0.5, and 0.7. While holding other variables constant, the gelled acid is injected into the core at various rates. The simulation results are presented in Figure 3, where columns (A) to (D) represent different power-law index values and rows (a) to (e) indicate injection rates ranging from low to high.

thumbnail Fig. 3

Effect of power-law index n on the structure of the dissolution. (A) n = 0.1, (B) n = 0.3, (c) n = 0.5, (D) n = 0.7. The rate of gelled acid injection in different rows are: (a) 1/Da = 10−9, (b) 1/Da = 10−6, (c) 1/Da = 10−4, (d) 1/Da = 10−3, (e) 1/Da = 1.

In row (a) of Figure 3, face dissolution occurs when 1/Da = 10−9. As shown in row (b), when 1/Da = 10−6, conical dissolution patterns are formed. Rows (c) and (d) in Figure 3 depict the formation of wormholes when 1/Da = 10−4 and 1/Da = 10−3, respectively. In row (e) of Figure 3, a ramified wormhole is formed when 1/Da = 1. The breakthrough volume (PVbt ) under different injection rates and power-law indices is illustrated in Figure 4.

thumbnail Fig. 4

Effect of power-law index n on the breakthrough volume.

Examining column (A) in Figure 3, we observe that under different injection rates, the branching of wormholes is more prominent for n of 0.1 compared to the other three conditions. This behavior can be attributed to the gelled acid’s viscosity gradually decreasing with rising shear stress (Greater than the critical shear stress) when the power-law index is less than 1. Generally speaking, the viscosity is more susceptible to shear stress the smaller the power-law index is. As a result, gelled acid with a power law index value of 0.1 has the highest sensitivity. Due to the rock’s heterogeneity, the different regions’ permeability is different. This leads to the gelled acid spreading to highly permeable regions. This high permeability results in greater shear stress in these regions. The viscosity of the gelled acid decreases dramatically and becomes more fluid, allowing more acid to flow into these areas. This uneven acid dissolution process results in the branching phenomenon of wormholes. Therefore, compared to acids with higher power-law indices, those with lower power-law indices exhibit a more uniform dissolution pattern.

At low injection rates, the breakthrough volumes (PVBT) of acids with different power-law indices are relatively similar, resulting in face dissolution and conical dissolution. Under conditions of moderate injection rates, the breakthrough volume (PV bt) corresponding to n = 0.3 is the smallest. However, as shown in Figure 3 (row (c), column (B)) and (row (d), column (B)), the resulting wormholes are short and exhibit poor branching. High-permeability channels formed in these cases do not effectively enhance reservoir conditions. Conversely, acids with power-law indices of 0.5 and 0.7 exhibit better dissolution effects.

Furthermore, it can be observed from the figures that regardless of the dissolution mode, when the injected acid comes into contact with fractures, it preferentially grows and develops along them. Fractures provide relatively low-resistance channels, enabling the acid to penetrate the rock more rapidly. This growth and development process inhibits the formation of other wormholes because the acid concentration and flow rate in other areas are lower compared to fractures, resulting in relatively weak dissolution. Thus, fractures play a guiding and concentrating acid role in the dissolution process, preventing the formation of wormholes in other locations. Consequently, the injected acid cannot uniformly penetrate all parts of the carbonate reservoir, leading to reduced uniformity in the treatment effect.

5.3 Effect of fracture parameters

5.3.1 Fracture density

This subsection investigates the effect of fracture number on wormhole propagation by varying the number of fractures Nf. The fracture’s orientation and length were kept constant, while the number of fractures ranged from 6 to 30. The fracture length was set as 2 R/3, with a standard deviation is 20° and an average orientation is 60°. Each numerical simulation has a different fracture length and orientation because fractures are generated at random.

In Figure 5, Column (A) illustrates the initial location of the vugs and fractures, with the vugs fixed. Column (B) shows a comparison of the dissolution structure of acid breakthrough cores at different fracture numbers. From Figure 5, it can be observed that at a small number of fractures, such as 6, the distribution of fractures appears sparse, with individual fractures separated from each other. During the propagation of the wormhole, the acid must dissolve a portion of the matrix to establish connections between fractures and vugs. The wormhole primarily grows along the vugs, which become part of the wormhole and contribute to the formation of more branches. This is because the vugs have more permeability than the matrix, which causes the acid to flow into the vugs preferentially. Thus, when there are few fractures, the growth of the wormhole is primarily controlled by the vugs. Additionally, the volume of acid breakthrough is the greatest at a fracture number of 6.

thumbnail Fig. 5

Fracture number’s impact on the structure of the dissolution. (A) Distribution of vugs and fractures during initial dissolution. (B) dissolution structure when acid breakthrough. (a) Nf = 6, (b) Nf = 12, (c) Nf = 20, (d) Nf = 30.

The connectedness between fractures gets better as the number of fractures rises. Consequently, the impact of vugs diminishes. Fractures become more dominant in the growth of the wormhole, and the injected gelled acid flows predominantly along the fractures. When there are 30 fractures, the effect of vugs is almost negligible. The injected acid directly reaches the outlet from the inlet along the fractures, largely bypassing contact with the matrix. The resulting wormhole structure is formed primarily along a few fractures, while other areas receive less treatment, limiting the extent of acid coverage throughout the reservoir. Moreover, Figure 6 demonstrates that the breakthrough volume (PV bt) decreases with the increasing number of fractures at the same injection rate. When there are 30 fractures, the corresponding breakthrough volume (PV bt) is smallest. This is because dissolution within the fractures causes the acid to pass through quickly, reducing the amount of acid dissolved into other areas of the rock.

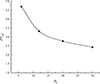thumbnail Fig. 6

The injected acid’s breakthrough volume corresponding to different fracture number.

Furthermore, as depicted in Figure 5 (Column (B)), when the dissolution process is complete, it will be found that the gelled acid does not pass through every fracture. Only a portion of the fractures becomes part of the wormhole. Fractures closer to the core are more likely to be accessible to the acid, while fractures at the edges of the core are rarely affected by the acid.

5.3.2 Fracture orientation

This subsection investigates the fracture orientation’s influence on the wormhole’s structure. In this case, the number and length of fractures were kept constant. Specifically, there were 20 fractures with a length of 2 R/3, a standard deviation of 5°, and the values of θf were set to 0°, 30°, 90°, and 150°, as shown in Figure 7 (Column (A)). The resulting wormhole structures corresponding to different fracture orientations are presented in Figure 7 (Column (B)).

thumbnail Fig. 7

Varying fracture orientation’s influences on the structure of the dissolution. (A) Distribution of fractures and vugs during the initial dissolution (B) dissolution structure when gelled acid breakthroughs. (a) θf = 0°, (b) θf = 30°, (c) θf = 90°, (d) θf = 150°.

From Figure 7, it can be observed that when the fracture orientation is 0°, as depicted in Figure 7 (row (a), column (B)), the fracture direction runs parallel to the wormhole’s growth direction. Injection’s gelled acid dissolves a portion of the rock and then connects with the fracture. The wormhole primarily grows in the direction of the fracture, resulting in a thin wormhole with fewer branches. The final wormhole generated aligns with the radius of the core.

When the fracture orientation is 30° or 150° (−30°), as shown in Figure 7 (row (b), column (B)) and (row (d), column (B)), respectively, the wormhole still grows in the direction of the fracture, but with more branching. In contrast, when the fracture orientation is perpendicular to the core radius, as shown in Figure 7 (row (c), column (B)), the branching of the wormhole is strongest. The wormhole no longer grows in the same direction as the fracture. After passing through the vertical fracture, the injected acid extends along the matrix, following the path of least resistance for penetration.

In conclusion, for radial flow, the wormhole’s growth direction depends on the core’s radius direction. The orientation of the fracture does not solely determine the development direction of the wormhole; however, it does influence the growth path and the final morphology of the wormhole. The interaction between the fracture orientation and the injection process leads to variations in the branching pattern and the overall structure of the wormhole.

5.3.3 Fracture length

The fracture length’s impact on the structure of the wormhole is examined in this subsection. The study keeps the number of fractures and the fracture orientation constant. Specifically, there are 20 fractures with a standard deviation of 20°, and the lengths are taken as 2R/6, 2R/3, and 2R, as depicted in Figure 8 (Column (A)). Figure 8 (Column (B)) displays generated wormhole structures corresponding to various fracture lengths.

thumbnail Fig. 8

Analysis of the impact of fracture length of (a) 2 R/6, (b) 2 R/3, (c) 2 R on dissolution structures. (A) Distribution of fractures and vugs during the initial dissolution (B) dissolution structure when acid breakthrough.

When the fractures are short, as illustrated in Figure 8 (row (a), column (B)), the acid dissolves a portion of the matrix and then connects with the fracture. The resulting wormhole is relatively wide, exhibits branching, and possesses an erratic growth pattern. As the fracture length increases, as shown in Figure 8 (row (b), column (B)) and (row (c), column (B)), the dissolution area of the wormhole decreases, and the branching becomes weaker. The generated wormhole assumes a more regular shape. Because the fractures are more permeable than the matrix, the acid preferentially flows into the fractures during the acid-rock reaction. When fracture length reaches the edge of the core, the injected gelled acid can break through the core more rapidly. Consequently, the breakthrough volume gradually decreases as the fracture length grows. The wormhole lines up with the fracture’s direction, which becomes an integral part of the wormhole structure.

5.4 Effect of vug size

This subsection investigates the impact of vug size on dissolution structure. Figure 9 shows the outcomes of the simulations. The corresponding dissolution structures of the vug distributions are illustrated in Figure 9 (column (B)).

thumbnail Fig. 9

Two-dimensional distribution of vug (A) and dissolution structures (B) at (a) lx = 0.05, ly = 0.05; (b) lx = 0.1, ly = 0.1; (c) lx = 0.2, ly = 0.2.

From Figure 9 (column (B)), it is evident that, regardless of size, the injected acid does not preferentially flow into the vugs. Only a subset of vugs within the dissolution structure participates in the reaction, while the remaining unreacted vugs remain intact. The growth and propagation of wormholes mainly occur in the direction of fractures, rather than along the vug direction. This finding implies that vugs have little to no impact on wormhole propagation. On the contrary, fractures play a more crucial role in the carbonate rocks’s reaction flow process, as they facilitate the propagation and interconnection of wormholes.

As depicted in Figure 9, the injected acid dissolves a portion of the matrix first and then connects the vugs and the fractures. Fractures serve as highly permeable channels for acid injection, enabling the acid to flow preferentially through the channels with the least resistance. This preferential flow inhibits the acid from reaching other areas. Due to their ability to extend over longer distances and occur in greater numbers, fractures have a more pronounced influence on fluid permeability and the propagation of wormholes in rocks. Conversely, the number of vugs is limited, and their sizes are relatively small, resulting in a comparatively minor effect on wormhole propagation.

6 Conclusion

In this paper, a T-H-C coupled model is established to simulate the reaction flow process in deep-buried carbonate rocks with vugs and fractures. Analysis of the influence of the rheological properties, fracture-vuggy parameters on the propagation of the gelled acid wormhole from a two-dimensional radial flow perspective has led to the following conclusions:

  1. Gelled acid with a lower power-law index exhibits a more uniform dissolution pattern compared to that with a higher power-law index. This uniform reaction flow enhances the efficiency and effectiveness of the entire treatment process.

  2. Carbonate rocks with fractures are more susceptible to acid erosion compared to rocks without fractures.

  3. Carbonate rocks often contain fractures and vugs, and their existence alters the flow dynamics of injected acid. They significantly affect the distribution and transport efficiency of gelled acids in rocks. Among them, fractures have a higher influence on the growth and evolution of wormholes compared to vugs.

  4. In cases with fewer fractures, wormholes predominantly grow along vugs. But as the quantity of fractures rises, the influence of vugs diminishes while fractures become more significant. Therefore, in carbonate reservoirs with well-developed vugs, the focus can be placed on utilizing these vugs to promote wormhole propagation. On the other hand, if there are significant fractures concentrated around the wellbore, it is advisable to seal these fractures to achieve a more uniform treatment effect.

  5. When fractures are perpendicular to the radial direction, they hinder wormhole propagation. Conversely, when the angle between fractures and the radial direction is smaller, wormhole propagation is promoted. Hence, in the study of reactive flows, priority should be given to areas where fractures are approximately parallel to the radial direction. Fractures in these areas are more likely to contribute to wormhole propagation and have a greater impact on the results.

  6. Increasing the fracture length leads to a faster growth rate of the wormhole but weaker branching. To ensure better dissolution effects in practical applications, sealing of long fractures can be conducted prior to acid injection.

  7. Vug size has only a small impact on wormhole growth. Regardless of vug size, the dissolution pattern remains unchanged.

Although the presence of fractures can accelerate acid penetration and dissolution, too many fractures may lead to problems of uneven acid distribution and small coverage. In conclusion, since gelled acids have limited effectiveness in deep-buried reservoirs with numerous fractures, the focus of our future work has shifted to self-diverting acid. Exploring the potential of self-diverting acids in reservoirs with complex fracture networks.

Funding

Thanks to the support of the National Natural Science Foundation of China No.52374036, Natural Science Foundation of Shandong Province No. ZR2023ME207, 111 Project under No. B08028.

Conflicts of interest

The authors declare no competing relevant financial or non-financial interests.

References

  • Liu P., Yao J., Couples G.D., Ma J., Iliev O. (2017) 3-D modelling and experimental comparison of reactive flow in carbonates under radial flow conditions, Sci Rep 7, 17711. [CrossRef] [PubMed] [Google Scholar]
  • Morad S., Al-Ramadan K., Ketzer J.M., Ros L.F.D. (2010) The impact of diagenesis on the heterogeneity of sandstone reservoirs: A review of the role of depositional facies and sequence stratigraphy, AAPG Bull 94, 1267–1309. [CrossRef] [Google Scholar]
  • Zhang R., Yao G., Shou J., Zhang H., Tian J. (2011) An integration porosity forecast model of deposition, diagenesis and structure, Shiyou Kantan Yu Kaifa/Petrol Explor Dev 38, 145–151. [Google Scholar]
  • Siebach K.L., Grotzinger J.P., Kah L.C., Stack K.M., Malin M., Léveillé R., Sumner D.Y. (2015) Subaqueous shrinkage cracks in the sheepbed mudstone: implications for early fluid diagenesis, gale crater, mars, J Geophys Res Planets 119, 1597–1613. [Google Scholar]
  • Kiraly L., (2002) Karstification and groundwater flow. In: Gabrovsek, F. (Ed.), Evolution of Karst: from Prekarst to Cessation. Postojna-Ljubljana: Institut za raziskovanje krasa, ZRC SAZU: 155–90. [Google Scholar]
  • Kaufmann G., Braun J. (2000) Karst aquifer evolution in fractured, porous rocks, Water Resour Res 36, 1381–1391. [CrossRef] [Google Scholar]
  • Dubois C., Bini A., Quinif Y. (2022) Karst morphologies and ghostrock karstification, Geomorphologie 28, 13–31. [CrossRef] [Google Scholar]
  • Johnson J.W., Nitao J.J., Knauss K.G. (2004) Reactive transport modelling of CO2 storage in saline aquifers to elucidate fundamental processes, trapping mechanisms and sequestration partitioning, Geol Soc London Spec Publ 233, 107–128. [CrossRef] [Google Scholar]
  • Lagneau V., Pipart A., Catalette H. (2005) Reactive transport modelling and long term behaviour of CO2 sequestration in saline aquifers, Oil Gas Sci Technol 60, 231–247. [CrossRef] [Google Scholar]
  • Kang Q., Lichtner P.C., Viswanathan H.S., Abdel-Fattah A.I. (2010) Pore scale modeling of reactive transport involved in geologic CO2 sequestration, Trans Porous Media 82, 197–213. [CrossRef] [Google Scholar]
  • Islam A., Sun A.Y., Yang C. (2016) Reactive transport modeling of the enhancement of density-driven CO2 convective mixing in carbonate aquifers and its potential implication on geological carbon sequestration, Sci Rep 6, 24768. [CrossRef] [PubMed] [Google Scholar]
  • Gao G., Fu B., Zhan H., Ma Y. (2013) Contaminant transport in soil with depth-dependent reaction coefficients and time-dependent boundary conditions, Water Res 47, 2507–2522. [CrossRef] [PubMed] [Google Scholar]
  • Banaei S., Javid A., Hassani A. (2021) Numerical simulation of groundwater contaminant transport in porous media, Int J Environ Sci Technol 18, 151–162. [Google Scholar]
  • Ozgen-Xian I., Navas-Montilla A., Dwivedi D., Molins S. (2021) Hyperbolic reformulation approach to enable efficient simulation of groundwater flow and reactive transport, Environ Eng Sci 38, 181–191. [CrossRef] [Google Scholar]
  • Kang Q., Zhang D., Chen S. (2003) Simulation of dissolution and precipitation in porous media, J Geophys Res Solid Earth 108, B10, 2505. [Google Scholar]
  • Kang Q., Lichtner P.C., Zhang D. (2006) Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media, J Geophys Res Solid Earth 111, B05203. [Google Scholar]
  • Dong K. (2018) A new wormhole propagation model at optimal conditions for carbonate acidizing, J Pet Sci Eng 171, 1309–1317. [CrossRef] [Google Scholar]
  • dos Santos Lucas C.R., Neyra J.R., Araüjo E.A., da Silva D.N.N., Lima M.A., Ribeiro D.A.M., Aum P.T.P. (2023) Carbonate acidizing – a review on influencing parameters of wormholes formation, J Pet Sci Eng 220, 111168. [CrossRef] [Google Scholar]
  • Frick T., Mostofizadeh B., Economides M. (1994) Analysis of radial core experiments for hydrochloric acid interaction with limestones, in: SPE Formation Damage Control Symposium, OnePetro, pp. 1–6. [Google Scholar]
  • Bazin B. (2001) From matrix acidizing to acid fracturing: a laboratory evaluation of acid/rock interactions, SPE Prod Facil 16, 22–29. [CrossRef] [Google Scholar]
  • Dong K., Jin X., Zhu D., Hill A. (2014) The effect of core dimensions on the optimum acid flux in carbonate acidizing, in: SPE International Symposium and Exhibition on Formation Damage Control, OnePetro, pp. 1–10. [Google Scholar]
  • Karale C., Beuterbaugh A., Pinto M., Hipparge G., Prakash A. (2016) Hp/HT carbonate acidizing – recent discoveries and contradictions in wormhole phenomenon, in: Offshore Technology Conference Asia, OnePetro, pp. 1–23. [Google Scholar]
  • Cheng H., Zhu D., Hill A. (2017) The effect of evolved CO2 on wormhole propagation in carbonate acidizing, SPE Prod Oper 32, 325–332. [Google Scholar]
  • Golfier F., Zarcone C., Bazin B., Lenormand R., Lasseux D., Quintard M. (2002) On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium, J Fluid Mech 457, 213–254. [Google Scholar]
  • Panga M.K., Ziauddin M., Balakotaiah V. (2005) Two-scale continuum model for simulation of wormholes in carbonate acidization, AIChE J 51, 3231–3248. [CrossRef] [Google Scholar]
  • Kalia N., Balakotaiah V. (2007) Modeling and analysis of wormhole formation in reactive dissolution of carbonate rocks, Chem Eng Sci 62, 919–928. [CrossRef] [Google Scholar]
  • Cohen C.E., Ding D., Quintard M., Bazin B. (2008) From pore scale to wellbore scale: Impact of geometry on wormhole growth in carbonate acidization, Chem Eng Sci 63, 3088–3099. [CrossRef] [Google Scholar]
  • Kalia N., Glasbergen G. (2009) Wormhole formation in carbonates under varying temperature conditions, in: 8th European Formation Damage Conference, OnePetro, pp. 1–19. [Google Scholar]
  • Kalia N., Glasbergen G. (2010) Fluid temperature as a design parameter in carbonate matrix acidizing, in: SPE Production and Operations Conference and Exhibition, OnePetro, pp. 1–21. [Google Scholar]
  • Liu M., Zhang S., Mou J. (2012) Effect of normally distributed porosities on dissolution pattern in carbonate acidizing, J Pet Sci Eng 94, 28–39. [CrossRef] [Google Scholar]
  • Liu P., Xue H., Zhao L., Zhao X., Cui M. (2016) Simulation of 3D multi-scale wormhole propagation in carbonates considering correlation spatial distribution of petrophysical properties, J Nat Gas Sci Eng 32, 81–94. [CrossRef] [Google Scholar]
  • Bastami A., Pourafshary P. (2016) Development of a new model for carbonate matrix acidizing to consider the effects of spent acid, J Energy Res Technol 138, 1–13. [CrossRef] [Google Scholar]
  • Yuan T., Ning Y., Qin G. (2016) Numerical modeling and simulation of coupled processes of mineral dissolution and fluid flow in fractured carbonate formations, Trans Porous Media 114, 747–775. [CrossRef] [Google Scholar]
  • Wei W., Varavei A., Sepehrnoori K. (2017) Modeling and analysis on the effect of two-phase flow on wormhole propagation in carbonate acidizing, SPE J 22, 2067–2083. [CrossRef] [Google Scholar]
  • Mahmoodi A., Javadi A., Sola B.S. (2018) Porous media acidizing simulation: New two-phase two-scale continuum modeling approach, J Pet Sci Eng 166, 679–692. [CrossRef] [Google Scholar]
  • Babaei M., Sedighi M. (2018) Impact of phase saturation on wormhole formation in rock matrix acidizing, Chem Eng Sci 177, 39–52. [CrossRef] [Google Scholar]
  • Trabucchi M., Garcia D.F., Carrera J. (2023) Visualizing and evaluating wormholes formation dynamics under flow competition in an intermediate-scale dissolution experiment, Sci Total Environ 867. [Google Scholar]
  • Maheshwari P., Balakotaiah V. (2013) Comparison of carbonate HCL acidizing experiments with 3D simulations, SPE Prod Oper 28, 402–413. [Google Scholar]
  • Lv Y., Wei P., Zhu X., Gan Q., Li H. (2021) THMCD modeling of carbonate acdizing with HCL acid, J Pet Sci Eng 206, 108940. [CrossRef] [Google Scholar]
  • Gao B., Li Y., Pang Z., Huang T., Kong Y., Li B., Zhang F. (2024) Geochemical mechanisms of water/CO2-rock interactions in EGS and its impacts on reservoir properties: a review, Geothermics 118, 102923. [CrossRef] [Google Scholar]
  • Berrezueta E., Kovacs T., Herrera-Franco G., Mora-Frank C., Caicedo-Potosí J., Carrion-Mero P., Carneiro J. (2023) Laboratory studies on CO2-brine-rock interaction: an analysis of research trends and current knowledge, Int J Greenhouse Gas Control 123, 103842. [CrossRef] [Google Scholar]
  • Gaus I. (2010) Role and impact of CO2-rock interactions during CO2 storage in sedimentary rocks, Int J Greenhouse Gas Control 4, 73–89. [CrossRef] [Google Scholar]
  • Li N., Zeng F.B., Li J., Zhang Q., Feng Y., Liu P. (2016) Kinetic mechanics of the reactions between HCL/HF acid mixtures and sandstone minerals, J Nat Gas Sci Eng 34, 792–802. [CrossRef] [Google Scholar]
  • Gomaa I., Mahmoud M., Kamal M.S. (2020) Sandstone acidizing using a low-reaction acid system, J Energy Res Technol 142, 103008. [CrossRef] [Google Scholar]
  • Gomaa I., Mahmoud M., Kamal M.S. (2020) Novel approach for sandstone acidizing using in situ-generated hydrofluoric acid with the aid of thermochemicals, ACS Omega 5, 1188–1197. [CrossRef] [PubMed] [Google Scholar]
  • Safari A., Dowlatabad M.M., Hassani A., Rashidi F. (2016) Numerical simulation and X-ray imaging validation of wormhole propagation during acid core-flood experiments in a carbonate gas reservoir, J Nat Gas Sci Eng 30, 539–547. [CrossRef] [Google Scholar]
  • Seigneur N., Mayer K.U., Steefel C.I. (2019) Reactive transport in evolving porous media, Rev Mineral Geochem 85, 197–238. [CrossRef] [Google Scholar]
  • Kalia N., Balakotaiah V. (2009) Effect of medium heterogeneities on reactive dissolution of carbonates, Chem Eng Sci 64, 376–390. [CrossRef] [Google Scholar]
  • Izgec O., Zhu D., Hill A.D. (2010) Numerical and experimental investigation of acid wormholing during acidization of vuggy carbonate rocks, J Pet Sci Eng 74, 51–66. [CrossRef] [Google Scholar]
  • Chen Y., Ma G., Li T., Wang Y., Ren F. (2018) Simulation of wormhole propagation in fractured carbonate rocks with unifled pipe-network method, Comput Geotech 98, 58–68. [CrossRef] [Google Scholar]
  • Khoei A., Sichani A.S., Hosseini N. (2020) Modeling of reactive acid transport in fractured porous media with the extended-fem based on Darcy-Brinkman-Forchheimer framework, Comp Geotech 128, 103778. [CrossRef] [Google Scholar]
  • Huang Z., Xing H., Zhou X., You H. (2020) Numerical study of vug effects on acid-rock reactive flow in carbonate reservoirs, Adv Geo-Energy Res 4, 448–459. [Google Scholar]
  • Liu P., Yao J., Couples G.D., Ma J., Huang Z., Sun H. (2017) Modeling and simulation of wormhole formation during acidization of fractured carbonate rocks, J Pet Sci Eng 154, 284–301. [CrossRef] [Google Scholar]
  • Qi N., Chen G., Liang C., Guo T., Liu G., Zhang K. (2019) Numerical simulation and analysis of the influence of fracture geometry on wormhole propagation in carbonate reservoirs, Chem Eng Sci 198, 124–143. [CrossRef] [Google Scholar]
  • Jia C., Sepehrnoori K., Zhang H., Yao J. (2021) Numerical studies and analyses on the acidizing process in vug carbonate rocks, Front Earth Sci 9, 712566. [CrossRef] [Google Scholar]
  • Asl A.M., Sedaee B., Kandowjani A.E. (2024) Fracture and vug effects on wormhole pattern during acidizing of triple porosity carbonate rocks, Geoenergy Sci Eng 232, 212417. [CrossRef] [Google Scholar]
  • Wang L., Mou J., Mo S., Zhao B., Liu Z., Tian X. (2020) Modeling matrix acidizing in naturally fractured carbonate reservoirs, J Pet Sci Eng 186, 106685. [CrossRef] [Google Scholar]
  • Liu P., Kong X., Feng G., Zhang K., Sun S., Yao J. (2023) Three-dimensional simulation of wormhole propagation in fractured-vuggy carbonate rocks during acidization, Adv Geo-Energy Res 7, 199–210. [Google Scholar]
  • Ratnakar R., Kalia N., Balakotaiah V. (2012) Carbonate matrix acidizing with gelled acids: An experiment-based modeling study, in: SPE International Production and Operations Conference & Exhibition, OnePetro, pp. 1–16. [Google Scholar]
  • Maheshwari P., Maxey J., Balakotaiah V. (2016) Reactive-dissolution modeling and experimental comparison of wormhole formation in carbonates with gelled and emulsified acids, SPE Prod Oper 31, 103–119. [Google Scholar]
  • Liu P., Li J., Sun S., Yao J., Zhang K. (2021) Numerical investigation of carbonate acidizing with gelled acid using a coupled thermal-hydrologic-chemical model, Int J Therm Sci 160, 106700. [CrossRef] [Google Scholar]
  • Liu P., Yan X., Yao J., Sun S. (2019) Modeling and analysis of the acidizing process in carbonate rocks using a two-phase thermal-hydrologic-chemical coupled model, Chem Eng Sci 207, 215–234. [CrossRef] [Google Scholar]
  • Liu P., Yao J., Couples G.D., Huang Z., Sun H., Ma J. (2017) Numerical modelling and analysis of reactive flow and wormhole formation in fractured carbonate rocks, Chem Eng Sci 172, 143–157. [CrossRef] [Google Scholar]
  • Panga M.K.R. (2003) Multiscale transport and reaction: two case studies, University of Houston. [Google Scholar]
  • Kalia N. (2008) Modeling and analysis of reactive dissolution of carbonate rocks, University of Houston. [Google Scholar]

All Tables

Table 1

List of parameter values for the simulation

In the text

All Figures

thumbnail Fig. 1

The dissolution modes of HCl and gelled acid were compared at different injection rates at 375 K. (A) HC1 (B) Gelled acid (a) initial fracture-vuggy structure, (b) 1/Da = 10−6, (c) 1/Da = 10−5, (d) 1/Da = 10−4, (e) 1/Da = 10−3, (f) 1/Da = 1.
In the text
thumbnail Fig. 2

The breakthrough volume required for HCl and gelled acid injection under different injection rate conditions.
In the text
thumbnail Fig. 3

Effect of power-law index n on the structure of the dissolution. (A) n = 0.1, (B) n = 0.3, (c) n = 0.5, (D) n = 0.7. The rate of gelled acid injection in different rows are: (a) 1/Da = 10−9, (b) 1/Da = 10−6, (c) 1/Da = 10−4, (d) 1/Da = 10−3, (e) 1/Da = 1.
In the text
thumbnail Fig. 4

Effect of power-law index n on the breakthrough volume.
In the text
thumbnail Fig. 5

Fracture number’s impact on the structure of the dissolution. (A) Distribution of vugs and fractures during initial dissolution. (B) dissolution structure when acid breakthrough. (a) Nf = 6, (b) Nf = 12, (c) Nf = 20, (d) Nf = 30.
In the text
thumbnail Fig. 6

The injected acid’s breakthrough volume corresponding to different fracture number.
In the text
thumbnail Fig. 7

Varying fracture orientation’s influences on the structure of the dissolution. (A) Distribution of fractures and vugs during the initial dissolution (B) dissolution structure when gelled acid breakthroughs. (a) θf = 0°, (b) θf = 30°, (c) θf = 90°, (d) θf = 150°.
In the text
thumbnail Fig. 8

Analysis of the impact of fracture length of (a) 2 R/6, (b) 2 R/3, (c) 2 R on dissolution structures. (A) Distribution of fractures and vugs during the initial dissolution (B) dissolution structure when acid breakthrough.
In the text
thumbnail Fig. 9

Two-dimensional distribution of vug (A) and dissolution structures (B) at (a) lx = 0.05, ly = 0.05; (b) lx = 0.1, ly = 0.1; (c) lx = 0.2, ly = 0.2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.