| Issue |
Sci. Tech. Energ. Transition
Volume 78, 2023
Selected Papers from First European Conference on Gas Hydrates (ECGH), 2022
|
|
|---|---|---|
| Article Number | 29 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.2516/stet/2023027 | |
| Published online | 19 October 2023 | |
Regular Article
An equation of state and a phase diagram for gas-hydrate-forming slurries in gas-shortage
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400 Orsay, France
* Corresponding author: michel.pons@lisn.fr
Received:
5
October
2022
Accepted:
31
August
2023
Slurries of gas hydrates, especially mixed hydrates of CO2 and TBPB (Tetra-n-Butyl Phosphonium Bromide), are currently under consideration for secondary refrigeration. Secondary refrigeration circuits contain wide sections where the two-phase slurry (solid + liquid), separated from the gas phase, undergoes transformations that would if gas were present, lead to both hydrate formation and gas dissolution. The absence of gas hinders these processes: the slurry is in gas shortage. The analysis demonstrates that, although thermodynamically distant from three-phase equilibria, slurries in gas-shortage are in equilibrium. For describing their thermodynamic state, the notion of CO2 partial pressure in a gas mixture is introduced, which leads to an equation of state and a new phase diagram with temperature or enthalpy versus CO2 mass-fraction. This diagram complements those commonly used for three-phase systems. The thermal behavior of slurries in gas shortage is then investigated, leading to the possibility of future experimental validation of the present analysis.
Key words: Gas-hydrate / Mixed-hydrate / Secondary refrigeration / CO2 / TBPB / Thermodynamics
© The Author(s), published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the vast majority of cooling units, based on mechanical compression and called direct or primary, heat is directly transferred from what needs to be cooled (air in cold chambers or air-conditioned apartments, streams in industrial processes, etc.) to the refrigerant fluid. Large primary cooling units like those in supermarkets or air-conditioned hotels however suffer from significant leaks of their refrigerant fluid, the global warming potential of which is very high. As a consequence, they are currently strongly regulated, if not banned. In secondary, or indirect refrigeration, a closed circuit filled with a secondary fluid, usually environment-friendly, is used for transferring heat to a primary unit, the size of which can be significantly reduced. The first environmental benefit results from the dramatic reduction of refrigerant leaks [1–4]. Secondary refrigeration may also bring economic benefits. In cases where cooling demand is concentrated on short periods of the day, e.g. restaurants or office buildings, producing cold at night and storing it for delivery on demand offers a threefold benefit: first, a primary cooling unit operated over a long period and in quasi-steady state can be down-sized, this reduces the investment cost; secondly, the nocturnal outdoor temperature is usually lower than the diurnal one, the energy efficiency of cold production is improved; lastly, electricity prices are usually reduced at night [5].
Two-phase slurries (suspensions of solid crystallites in a carrier liquid aqueous solution, herein abbreviated as SL), especially slurries of hydrate [6], are good phase-change materials for storing and transporting cold in secondary refrigeration circuits [2]. Hydrates (more exactly clathrate-hydrates) are crystals formed by water molecules arranged around large guest molecules of salt (from simple chlorides to quaternary salts) or of gas (e.g. CH4 or CO2) [7]. Mixed hydrates embed more than one kind of guest molecule. The mixed hydrate of CO2 + TBPB (Tetra-n-Butyl Phosphonium Bromide, a quaternary salt) is under special consideration in this article for two reasons. First, the latent heat of crystallization of the mixed-hydrate is about two-thirds that of ice: 200 kJ (kg_hydrate)−1; secondly, it can be operated in pressure and temperature ranges well-adapted to refrigeration purposes [8–15]. Secondary refrigeration is the framework where the issue addressed in this article arose.
In circuits designed for secondary refrigeration, only some specific sub-volumes are occupied by gas alone, e.g., gas blankets above slurry baths. The rest of the circuit is occupied by the slurry (herein, the word slurry may also name liquid solutions alone, where all the hydrate crystals would have decomposed). The slurry may be in contact with gas (e.g., in the storage tank), or not (e.g. in the tubing). It may also undergo transformations such as mechanical compression, cooling, heating, or mixing. When occurring in the presence of gas, some of those transformations generate new hydrate crystals, which then include CO2 molecules extracted from the gas phase. In numerical simulations, such transformations can be simulated with the help of three-phase equilibrium correlations. However, when the gas phase is absent, hydrate formation is hindered; the system thus departs from three-phase equilibrium and the usual equilibrium correlations are no longer valid. To the author’s best knowledge, the literature is silent about the thermodynamic description of slurries separated from their gas phase, herein said in gas shortage. Numerical simulations, at least, need such a description. The present article attempts a first-order approach to that issue. Only equilibrium states are considered: phenomena such as induction, metastability, supercooling, or kinetics are disregarded.
The present article is organized as follows. Secondary refrigeration circuits using mixed hydrates of TBPB + CO2 are first described, focusing attention on two situations where the slurry is put in gas shortage, especially mechanical compression. In order to better understand the difference between the presence and absence of gas, Section 3 recalls the thermodynamics of three-phase hydrate-forming systems, especially through the description of four processes for compressing such systems. Notations, expression of enthalpy, and phase diagrams are presented. Section 4 can then describe slurries in gas shortage: analysis, equation of state, and phase diagram. A short parametric study (influences of the total pressure and the global concentration of TBPB) is added. The discussion focuses attention on two aspects of slurries in gas shortage: mixing (the new phase diagram is very useful for calculating mixing processes), and heating (unexpected thermal effects are evidenced).
Before starting, here are some vocabulary clarifications. First, the word system herein denotes any set of the three components with prescribed proportions and where each phase is assumed to be uniform. In most cases, it will be an elementary volume enclosed in a much larger one, possibly non-uniform. It may also be a large volume where uniformity is ensured, e.g. by efficient stirring. Secondly, like in other articles [16], the salt TBPB is herein seen as an additive that stabilizes the hydrate-formation process by reducing pressure when compared to the case of a single hydrate of CO2 [10, 17].
2 Some gas-shortage situations in circuits for secondary refrigeration
2.1 Secondary refrigeration circuits for cold distribution
Figure 1 presents the process diagram of a secondary refrigeration circuit using a slurry of gas- or mixed-hydrate as a heat transfer medium. Between the primary cooling unit (not presented; it would be on the left side) and the various end-users on the right side, the gas-hydrate slurry is stored (tanks 1 and 2) and then distributed to the users via circuit 3 thanks to the main circulation pump 4. The liquid and solid phases have very close densities (they differ by less than 15–20%, cf. the Appendix). Consequently, if the solid fraction is not too high (below 35%) and if the flow is sufficiently turbulent to prevent crystal deposition, the slurry almost behaves like a single-phase fluid. Following the advisable rules for cold-distribution loops [18], such circuits are designed as unique loops along which the users are arranged in series [19]. For each end-user, a fraction of the main stream 3, extracted by an individual pump 5, flows through a heat exchanger 6 where it is heated (thus producing the cooling effect) before returning to the main loop. Two specific features can be pointed out. First, for each user, the position where the heated slurry returns to the main loop (point d in Fig. 1) is located upstream of the extraction point (point e). Another arrangement would make the flow velocity decrease in section c–e and would thus increase the risks of crystal deposition, agglomeration, and flow blockage [18, 21, 22]. Consequently, the slurry supplied to the heat exchanger (from point e) is a blend of the return stream (d) with the main one (c). Secondly, cyclone 7 is implemented between the user’s heat exchanger 6 and the return point d. The purpose is to separate the gas phase, generated in the heat exchanger by hydrate decomposition, from the remaining solid–liquid slurry and to let the latter return alone to the mainstream [20]. Indeed, as the density of the slurry and that of gaseous CO2 differ by two orders of magnitude, an amount of gaseous CO2 as small as 1% occupies the same volume as the other 99% made of solid and liquid phases. The same mass of gas (1%) is released when decomposing an amount of hydrate equal to 14%. This is approximately half the design value of hydrate mass-fraction contained in the storage tank. Without gas separation in cyclone 7, the gaseous volume fraction in the main circuit 3 would be very significant: the three-phase flow in the loop would then be very difficult to control, especially when aiming to supply the end-users located down-stream on the loop with as much slurry and as few gas as possible (gas has no cooling potential) [20].
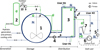 |
Figure 1 Process diagram of a secondary refrigeration circuit. 1–2: storage tanks (slurry plus gas); 3: distribution loop; 4: main pump; 5–6–7: cold supply devices for each end-user, resp. valve & pump, heat exchanger and cyclone; 8–9–10: control valve, compressor, and heat exchanger (see more details in ref. [20]); G: Gas phase; SL: Slurry (solid + liquid). |
2.1.1 Compressing a slurry in the absence of gas
In storage tank 1 of Figure 1, the slurry bath is stirred for the sake of homogeneity and covered by a gas blanket; let position a denote the interface slurry-gas. The flow supplied to the refrigeration loop is extracted from the tank at a position far below the free surface: it consists of solid and liquid phases alone (slurry SL). Compared to position a the latter flow is compressed, first by the hydrostatic pressure field in the storage tank, and secondly by the main circulation pump 4 that counterbalances the pressure drop in the circuitry downstream. Compression between the free surface a and the outlet of pump 4 (position b) seems to raise a paradox. Usually, when systems forming gas-hydrates are compressed, new hydrate crystals are generated and more gas dissolves into the liquid solution. Both phenomena transfer CO2 from the gas phase to the slurry. In the present compression, this twofold mass transfer cannot occur because the slurry has no contact with gas on its path from a to b: its total content of CO2 must remain constant. The slurry is thus said in gas-shortage, an expression which, in addition to solid-liquid suspensions, can also apply to liquid solutions alone, as soon as either is separated from the gas phase. Because of the absence of gas, no hydrate can be generated during that compression and the additive concentration in the solution x is constant: this compression is isosteric (unchanged concentrations). Moreover, it also is adiabatic (there is no heat transfer inside the tank), and isothermal (temperature is uniform in the tank). It will be seen in Section 3 that compression of three-phase systems cannot be altogether isosteric and isothermal.
2.1.2 Cooling a slurry in the absence of gas
A slurry undergoes gas shortage also when it is cooled in the absence of gas. This occurs in reactors designed for generating hydrate crystals [23] for refrigeration processes. Figure 2 schematically represents such a crystallizer. The slurry bath (SL) is covered by a gas blanket (G) and stirred for the sake of homogenization. It is also cooled by a heat exchanger (HX), herein a double-jacket one, in order to generate hydrate crystals. The dashed arrow in Figure 2 represents the convective motion induced when stirring the slurry bath. There are regions in the bath where convection pushes elements of slurry toward the boundary layer of the heat exchanger wall, where they are cooled. Usually, when the slurry is cooled, new hydrate crystals are generated and more gas dissolves into the liquid solution. As the convective movement develops below the interface a, those processes that would occur if gas were present cannot proceed because of the absence of gas: the slurry is locally in gas-shortage.
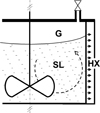 |
Figure 2 Reactor for generating gas-hydrate from a stirred three-phase system, slurry (SL) + gas (G), or for compressing it. The valve located on the lid can be used for adding gas into the reactor; the system temperature is controlled by the double-jacket heat exchanger (HX). |
3 Compression of the three-phase system Water + TBPB + CO2
Before describing slurries in gas shortage, thermodynamic bases of three-phase systems are recalled and applied to four basic processes of compression. It will show that hydrate generation (or decomposition) on the one hand, and dissolution of CO2 in the liquid solution on the other hand, interact with each other.
3.1 General presentation
The equilibrium variance of three-phase ternary systems is two. Two equilibria take place in the system H2O + TBPB + CO2. The first one rules the conditions for forming crystals of mixed hydrate of TBPB + CO2. The equilibrium temperature T depends on the gas pressure P and on the concentration x of TBPB in the aqueous solution according to the equation of state T = fTeq(P, x). In the region of interest, T increases with P and with x [9, 10, 17]. Secondly, CO2 dissolves in water [24]. The CO2 concentration in the aqueous solution, s, is described by the solubility state-function, s = fseq(P, T), which increases (almost linearly) with P and decreases with T [24]. When both equations of state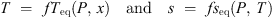 (1)are fulfilled, the three-phase system is in equilibrium. Equilibrium means that all the CO2 molecules, either dissolved in the liquid water, enclosed in the solid hydrate, or the gas phase have the same chemical potential. This equality is a cornerstone of the present approach.
(1)are fulfilled, the three-phase system is in equilibrium. Equilibrium means that all the CO2 molecules, either dissolved in the liquid water, enclosed in the solid hydrate, or the gas phase have the same chemical potential. This equality is a cornerstone of the present approach.
3.2 Notations used in this article
The complexity of the three-phase ternary system makes it necessary to clearly describe the notations used herein. The three phases, solid, liquid, and gaseous, are respectively denoted by the indexes S, L, and G; the indexes W, C, and A (A for Additive) respectively denote the three components, water, carbon dioxide, and TBPB. Any component proportion is defined by the corresponding mass-fraction χ● referred to the whole system, so that χ● = m●/mtotal where the symbol ● may represent one component (W, A, or C), one phase (L, S, or G), or one component in a given phase (e.g. χWL for the mass-fraction of water in the liquid phase). Concentrations in the solution, of additive or of dissolved CO2, are referred to the aqueous part, following the simple idea that neither TBPB nor CO2 alone can dissolve the other one; their presence only alters the equilibrium between water and the other component, i.e. modifies the equations of state (1). The additive concentration x and the CO2 solubility ratio s are thus defined as: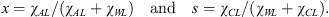 (2)
(2)
In the so-called initial state (index 0, no solid phase), the liquid solution contains the whole amounts of water and additive. One thus has: 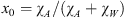 . The gas phase contains only CO2. The stoichiometry of the hydrate results from its crystal structure and is described by three invariant mass fractions YW, YA, and YC (in kg per kg crystal), the sum of which equals 1. They correlate the mass-fractions χ∙S to the solid mass-fraction χS according to:
. The gas phase contains only CO2. The stoichiometry of the hydrate results from its crystal structure and is described by three invariant mass fractions YW, YA, and YC (in kg per kg crystal), the sum of which equals 1. They correlate the mass-fractions χ∙S to the solid mass-fraction χS according to: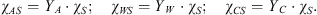 (3)
(3)
The additive concentration in the solid phase: xS = YA/(YA + YW) also is invariant. The following mass balances are straightforward: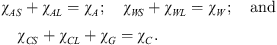 (4)
(4)
In the phase diagrams presented here under, domains or curves are designated by one, two, or three of the letters S, L, and G (for solid, liquid, and gas), always presented in the same order (S-L-G). The liquid phase is always present. Replacing the letter S, or G, with the symbol 0 (e.g. 0LG), means that the remaining phases (LG) would be in equilibrium with the phase designated by 0 (S), at the same temperature and pressure, if it were present. Similarly, “0L0” denotes a liquid phase alone that would be in equilibrium with the solid and gas phases if they were there.
3.3 Enthalpy of hydrate slurries in the framework of secondary refrigeration
3.3.1 Assumptions
Theoretically, the reference state for enthalpy should consider the three components separately. Assuming the ideality of aqueous solutions of TBPB allows us to consider two initial components, the solution of TBPB alone, and gaseous CO2. This simplification is moreover justified in the framework of secondary refrigeration. As mentioned above, a sufficient level of turbulence (high enough Reynolds number) is ensured everywhere in the circuit in order to protect it from flow blockage [21, 22]. Considering in addition that slurries behave like single-phase fluids [25], it may be stated that the solid and liquid phases always have the same velocity. This no-slip condition between those two dense phases also applies to the species, water, and additive. As a consequence, the global additive concentration in the slurry x0 = χA/(χW + χA) may be stated as constant and uniform along the circuit: this invariant only depends on initial decisions about the circuit design. As a result, the reference state for enthalpy is defined for that value of the additive concentration, the influence of which can nevertheless be investigated separately. Lastly, the only compressible phase in the considered range of operation is the gaseous one.
3.3.2 Expression of enthalpy
In the reference state, the whole carbon dioxide, in the gas phase, is separated from the aqueous solution of additive, assumed to be ideal. Once the values of x0 and of χC (mass-fraction of CO2 in the system) are prescribed, the mass-fractions of additive and water can be deduced from: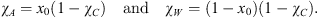 (5)
(5)
The reference pressure is P0 = 0.1 MPa, and the reference temperature is given by the equation of state: T00 = fTeq(P0, x0); T00 = 8.23 °C when x0 = 0.20.
Enthalpy of any current state (P, T, x0) is calculated in two stages. In the first one, both materials, aqueous solution, and gaseous CO2, are kept apart; they are compressed and heated to the state (P, T0, x0) where T0 = fTeq(P, x0). As the liquid solution is basically incompressible, its enthalpy is simply given by the sensible heat: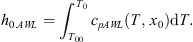 (6)
(6)
Enthalpy of gaseous CO2, a non-ideal gas, must account for the work of compression: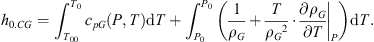 (7)
(7)
cpAWL and cpG are the specific heats of the liquid aqueous solution and gaseous CO2 respectively; ρG is the gas density. The enthalpy of the system at the end of the first stage h0 is: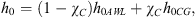 (8)it depends on P (both h0.AWL and h0.CG increase with P) and χC.
(8)it depends on P (both h0.AWL and h0.CG increase with P) and χC.
In the second stage, the system temperature changes from T0 to T while all the interactions between the solution and the gas (dissolution of CO2 and formation of hydrate crystals if T < T0) proceed. Involving the corresponding latent heats leads to the final expression of enthalpy: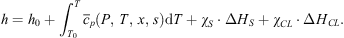 (9)
(9)
The average specific heat 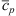 is decomposed as follows:
is decomposed as follows: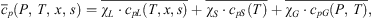 (10)where the values of P, T, x, s, χS, and χCL are their average values over that second stage.
(10)where the values of P, T, x, s, χS, and χCL are their average values over that second stage.
3.4 Compression of three-phase systems: four simple cases
3.4.1 A twofold phase diagram
The state variables temperature T, and gas pressure P, are independently related to the additive and CO2 concentrations in the liquid phase, x and s respectively. Actually, the phase diagrams related to hydrate formation and CO2 dissolution should be represented in three dimensions, [T-x-P] or [P-T-s], where the state functions (1) would be represented by surfaces. For CO2-solubility in water, Diamond and Akinfiev present the [P-T], [s-P], and [s-T] graphs, where the third variable is a parameter that generates isovalue-curves [24]. For hydrate equilibria, the three-dimensional correlation is most usually projected, either on the [T-x] graph for systems forming single salt-hydrates or mixed hydrates of gas + salt, or on the [P-T] graph for systems forming single gas-hydrates. Both graphs are presented in Figure 3, using the missing variable (resp. P and x) as a parameter. In the [T-x] diagram 3A, each value of gas pressure corresponds to one 0LG curve above which lies the liquid-gas domain LG at the corresponding pressure; the three-phase domain SLG lies below. Two of such curves (P = 0.5 and 0.3 MPa) are displayed, reproducing data published in refs. [8, 10]. The vertical line x = xS in Figure 3A is the domain S of solid hydrates. As the concentration x in the solution is always smaller than xS, hydrate formation reduces the concentration x in the solution. The [P-T] graph Figure 3B presents equilibrium isosters (correlation P-T at constant concentration x) with four equidistant values of x from 0.12 to 0.24. With respect to each of them, the SLG domain lies above and the LG domain below. The chosen pressure range (around 0.4 MPa) is mentioned as possibly relevant for air-conditioning purposes with that ternary system [20, 26]; it however just serves to develop the analysis below, which does not qualitatively depend on that arbitrary choice.
 |
Figure 3 Phase diagrams with equilibrium curves (dashed lines) for the system with mixed-hydrate of TBPB + CO2. A: [T-x] diagram with two 0LG curves (liquid solutions in equilibrium with both solid crystals and gaseous CO2) at 0.5 and 0.3 MPa. B: [P-T] diagram with four equidistant values of x. Solid arrows: four processes for compressing the three-phase system from 0.3 to 0.5 MPa: LV = isochoric; LX = isosteric; LA = adiabatic; LT = isothermal. |
3.4.2 Four compression processes
Four processes for compressing the three-phase system from 0.3 to 0.5 MPa are described and displayed in Figure 3. Their common initial state is P = 0.3 MPa and x = 0.20 (points L in Figs. 3A and 3B), where the slurry is assumed to contain enough crystals (point S in Fig. 3A) for the isochoric process below to fully develop. The corresponding global concentration of additive in the SL system, x0, is shown by the symbol “+” in Figure 3A. The four processes can be achieved with a reactor like that schematically described in Figure 2. In three of them, gas is added to the reactor through the valve located on the lid. The temperature of the whole system is regulated thanks to the heat-exchanger HX, assumed to transfer the exact heat quantity that fulfills the prescribed condition. The heat quantities involved in the four processes, calculated with the expression (9) for enthalpy, are presented in Table 1.
Heat quantities involved in the four compression processes displayed in Figure 3, in kJ for a system containing 1 kg of water, 275 g of TBPB plus as much gas as required in the gas phase. Initially, the system contains 100 g of hydrate crystals. Both hydrate decomposition and CO2 dissolution involve latent heat. Values are negative for exothermal phenomena.
The first process is isochoric, path LV in Figure 3. Compression is obtained by heating the closed reactor to the proper temperature. When heated, hydrate crystals tend to decompose and release gaseous CO2: the so-degassed CO2 increases the gas pressure, which in turn causes more CO2 to be dissolved in the solution; actually, part of the CO2 molecules released by hydrate decomposition remains dissolved in the solution. The heat balance, Table 1, shows that a small but non-negligible part (3%) of the heat demand is supplied by that dissolution.
In the second process, isosteric following the path LX, the additive concentration in the liquid solution is constant. This constancy means that the amount of hydrate is unchanged: pressure rise is obtained by injecting gas into the reactor. As there is no latent heat related to hydrate decomposition or crystallization, the heat demand is only for sensible heat. Note that about one-fourth of that demand is supplied by CO2 dissolution (see Tab. 1).
The third process is adiabatic, paths LA. The adiabatic condition is assumed to apply to the SLG system alone, and gas must be injected into the reactor. The sensible heat is mainly supplied by hydrate crystallization, but also and significantly by CO2-dissolution (almost 20%).
The fourth process is isothermal, paths LT. According to Figure 3A, isothermal compression needs the additive concentration in the liquid solution to significantly decrease. This is obtained by forming a large amount of hydrate, which requires a large input of CO2 into the reactor while extracting both latent heat of hydrate crystallization and CO2-dissolution.
These results show that, beyond exchanges with the gas phase during compression, hydrate formation (or decomposition) and dissolution of CO2 interact with each other within the solution, in terms of heat transfer, and of mass transfer. There is no reason for those interactions to cease when the gas phase is absent.
4 Slurries in gas-shortage: results and discussion
4.1 Thermodynamic analysis
4.1.1 Differences from three-phase systems
In three-phase systems, the state of the liquid solution is described by the state equations (1), and the word “pressure” means “gas-pressure”: compression results from forces exerted by the gas molecules on the interface with the solution. Such forces also tend to transfer CO2 into the solution and therefore induce hydrate generation and CO2 dissolution. However, when the slurry is separated from the gas phase, compression results from forces that either occur in the bulk of the solution (hydrostatic pressure field) or are exerted by a moving solid wall (mechanical pump). These forces do not transfer anything into the solution and have no effect on hydrate generation and CO2 dissolution. Their effect is strictly mechanical, and so are named such compressions in the following.
4.1.2 Thermodynamic representation and equation of state
According to Section 2.1.1, mechanical compression of slurries in gas shortage is altogether isosteric and isothermal. Pressure is thus the only state variable that changes. Consequently, slurries in gas shortage depart from three-phase equilibrium and their thermodynamic state differs from the state equations (1). To the author’s knowledge, this difference is not mentioned in the literature although there are processes where it occurs. Numerical simulations of such processes need a thermodynamic description of that state. Although the equations of state (1) are not fulfilled, slurries in gas shortage are not out-of-equilibrium. Indeed, without gas, there are only two phases, and the equilibrium variance of two-phase ternary systems equals 3 (instead of 2 for three-phase systems). Thanks to this additional degree of freedom, slurries in gas shortage are in equilibrium (and such states are indeed stable). If the corresponding equation of state differs from equation (1), it must maintain equality between the chemical potentials of CO2 molecules in the liquid and solid phases. The absence of gas allows us to imagine a virtual gas where the CO2 molecules would also have the same chemical potential. For the sake of thermal equilibrium, the temperature of that virtual gas must equal that of the slurry. However, its virtual pressure must be less than the effective mechanical pressure applied to the slurry. In Figure 1, the gas pressure at the free surface, position a, is only part of that at the exit of the main pump 4, position b. The distinction introduced above between gas pressure and mechanical pressure suggests that the virtual gaseous CO2 could be mixed with a completely inert gas (inert with respect to the three components). This suggestion leads to an analogy where the effective mechanical pressure is the total pressure of the virtual gaseous mixture while the gas pressure that rules equilibrium is the partial pressure of CO2 in that mixture. The so-introduced CO2 partial pressure is denoted as PC in the following. Stating now that the chemical potentials of CO2 in the solid and liquid phases are equal to that of gaseous CO2 at T and PC leads to the equation of the state of slurries in gas shortage:
There is a unique value of PC that fulfills both equations of state:
(11)where the temperature T and concentrations x and s take their effective values in the liquid solution according to the relevant mass balances.
Beyond mathematics, the partial pressure PC also has a physical significance: it is related to the total amount of CO2 contained in the slurry, i.e. to the mass-fraction χC in the system.
The equation of state (11) for slurries in gas-shortage is consistent with the interpretation of compression developed in Section 2.1.1: relating T, x, and s to the partial pressure PC, instead of the total one P, makes the latter free to change independently of the former four variables. Here is the additional degree of freedom mentioned above. The expression of enthalpy for three-phase systems, equations (6)–(10), still holds, except that now the carbon dioxide introduced as gas is completely incorporated into the slurry SL before the end of the so-called second stage. Moreover, the composition of the liquid phase, χ · L, and the solid mass-fraction, χS, now depend on the solution of equation (11) via the mass balances (2)–(4).
4.2 Phase diagram for slurries in gas-shortage
4.2.1 Description
In usual phase diagrams for systems with gas-hydrates, the gas phase is always present. The present concern is however to highlight two domains without gas: Liquid, and Solid–Liquid. The liquid phase is always present, with carbon dioxide dissolved in it.
The phase diagram Figure 4 is displayed in two complementary graphs, [T–χC] and [h–χC], both established for P = 0.5 MPa and x0 = 0.20. The central point (symbol ∙) is the purely liquid state 0L0 defined by the triplet (P, x0, T0 = fTeq(P, x0)), where both equations of state (1) are fulfilled: the total amount of CO2, χC, exactly corresponds to the amount dissolved in the solution at P and T0. The diagrams present the two well-known domains with gas, LG, and SLG, and between them the line 0LG (to the right of the central point), at constant temperature (P and x0 are prescribed) but slightly decreasing enthalpy (see the tabulated data in the Appendix). Indeed, the enthalpy of gas, h0.CG, is less than that of the solution, h0.AWL, see equation (8).
 |
Figure 4 Phase diagram for slurries in gas-shortage, at 0.5 MPa and with x0 = 0.20. Two graphs: A [T-χC] and B [h-χC]. Notations: S = Solid; L = Liquid; G = gas. The partial pressure PC is constant (0.4 MPa) along the dashed curves. |
In those two domains with gas, increasing the CO2 mass-fraction χC just adds gas to the system without changing anything in the liquid solution. In the three-phase domain SLG, reducing the system temperature increases both the amount of CO2 dissolved in the solution and the amount of hydrate: the gaseous mass-fraction forcedly decreases. The SLG domain then presents a lower limit, SL0, where the CO2 contained in the system exactly corresponds to the CO2 encaged in the hydrate crystals plus that dissolved in the solution, according to equation (1). Below the SL0 curve, the system can only be two-phase, SL, and thus in gas-shortage.
Considering temperatures above that of the central point 0L0, the solubility of CO2 decreases when temperature increases [24]. So does the maximal amount of CO2 contained in the solution: the line L0 is not vertical but slightly to the left. On its left side lies the liquid domain L, where the liquid solution contains dissolved CO2 but not as much as it could: it is in gas shortage and the corresponding CO2 partial pressure PC is the solution to the problem:![$$ {{fs}}_{{eq}}\left({P}_C,T\right)=s={\chi }_C/\left[1-{x}_0\left(1-{\chi }_C\right)\right] $$](/articles/stet/full_html/2023/01/stet20220168/stet20220168-eq14.gif) (12)where the solubility s is related to the CO2 mass-fraction χC via the mass-balances (2) and (5).
(12)where the solubility s is related to the CO2 mass-fraction χC via the mass-balances (2) and (5).
The domains in gas-shortage, L and SL, are separated by the 0L line, where equations (11) and (12) are fulfilled together with x = x0 (there is no hydrate). Figure 4 also presents the correlations [T, or h, vs. χC] in the L and SL domains for a prescribed value of PC (0.4 MPa, i.e. 80% of the total pressure).
Lastly, the extension of the abscissa axis (χC = 0.02: 2% of the whole mass consists of CO2) can be related to a value of the hydrate mass fraction. Among the total mass of CO2, about 0.009 is dissolved (value of χC for the central point 0L0, where χC ≡ χCL). The complement can only be enclosed in hydrate crystals (there is no gas), i.e. χCS ≈ 0.011. With YC = 0.071 (crystal stoichiometry), the corresponding mass-fraction of mixed-hydrate χS is close to 0.15. Although focused on the domains in gas-shortage, L, and SL, those graphs encompass a large part of the domain of interest for processes with hydrate-forming slurries.
4.2.2 Respective influences of the total pressure P and global additive concentration x0
As a short parametric study, Figure 5 shows how the four domains of Figure 4 are modified when either the total pressure or the global additive concentration, decreases (short dashes for P = 0.3 MPa; long dashes for x0 = 0.15).
 |
Figure 5 Respective influences of either the total pressure P or the global additive concentration x0, on the phase diagram of Figure 4. Same graphs, notations, and solid lines as in Figure 4. Short dashes “ P ”: P = 0.3 MPa, x0 = 0.20; long dashes “ x 0”: x0 = 0.15, P = 0.5 MPa. |
When the total pressure P decreases, the solution dissolves less CO2, and the temperature T0 = fTeq(P, x0) decreases: the central point moves toward lower temperatures and lower CO2 mass fractions. Nevertheless, both 0L lines are exactly preserved, consistently with the state equations plus incompressibility of the liquid phase. The other three curves are globally similar to the initial ones.
The main effect of reducing x0 is to decrease the temperature T0 of the central point (see Fig. 3A), which in turn slightly increases the amount of dissolved CO2 (the abscissa) for the central point. The extension of the SLG domain results from the steeper slope of the 0LG equilibrium curves when x0 decreases, as can be observed in Figure 3A. One point must also be noticed: changing x0 also changes the reference temperature T00 [T00 = fTeq(P, x0)], therefore enthalpies of systems with different values of x0 cannot be directly compared.
4.3 Calculating mixing of slurry streams in gas-shortage
It has been widely mentioned above that the slurry supplied to the refrigeration circuit (at point b in Fig. 1) is in gas shortage. When moving further on the main loop 3, that slurry eventually reaches point c where it meets another stream (point d), which returns from heat-exchanger 6 and cyclone 7. Between points c–d, and point e, the two gasless streams mix. They differ in hydrate- and CO2-mass-fractions χS and χC (due to crystal decomposition in the heat exchanger and gas separation in the cyclone), also in temperatures, and consequently in additive-concentrations x in their liquid phases. As the resulting stream e is the one supplied to the heat exchanger 6, it is important to determine its thermophysical state. The global component mass-fractions (χW, χA, χC) and the enthalpy of the mixed stream are linear combinations of those of the inlet flows, weighed by the respective mass-flowrates. That linear combination is fully represented in the diagram [h-χC], i.e., in Figure 4B where point e exactly lies on the straight line between points c and d. Point c surely lies within the SL domain (gas-shortage), but point d lies either on the SL0 line (when hydrate crystals are still present), or on the L0 line (no hydrate). The example displayed in Figure 4B clearly shows that, depending on the positions of points c and d and the flow-rate ratio, point e may lie in the three-phase SLG domain, but also in the Liquid–Gas domain, or the Solid–Liquid domain, i.e., in gas-shortage. In each case, the equations to be solved and the resolution scheme for determining the thermodynamic state at point e (temperature and phase composition) are different. Fortunately, phase diagram 4B straightforwardly shows in which domain point e lies, and therefore which method must be used for calculating it. This feature was one part of the initial motivation for the present thermodynamic analysis: modeling how slurries locally in gas-shortage behave in secondary refrigeration circuits, especially when mixing.
4.4 Heating slurries in gas-shortage after mechanical compression
Modeling slurries in gas shortage just at the entrance of heat exchangers 6 was another motivation: how do slurries in gas shortage behave when receiving heat? In this section, calculations are done for a slurry with x0 = 0.2 and χC = 0.02, initially in gas-shortage with P = 0.5 MPa and PC = 0.4 MPa (see the point “+” in graph 4A), isolated (no mass transfer with the surroundings) and heated. When the slurry temperature rises, so does the partial pressure PC. As long as PC is less than P, the slurry remains in gas shortage (i.e., within the SL domain of Fig. 4). When PC eventually reaches equality with P, the slurry is on the SL0 curve and no longer in gas shortage: immediately beyond this point, the gas phase is present. Between those two points (PC = 0.4 MPa and 0.5 MPa), temperature increases by 0.74 K. Solving the problem (11) for the former point and problem (1) for the latter leads to the respective values of x and s: both increase with temperature, see Table 2. The concentration x increases when some hydrate crystals decompose and s increases when more CO2 is dissolved into the solution. These two processes develop simultaneously and in the absence of gas: all the molecules released by the decomposition of hydrate crystals, including CO2, are immediately incorporated by the liquid phase and no gas is generated. Hydrate decomposition and CO2-dissolution involve latent heat to be accounted for in the enthalpy balance. The amounts of decomposed hydrate and dissolved CO2 are such that the global effect of latent heat is endothermal and larger (in this case) than the sensible heat: it represents 58% of the total enthalpy change (see Tab. 2).
Thermal effects when heating a slurry, initially in gas-shortage by mechanical compression (P = 0.5 MPa and PC = 0.4 MPa), until it reaches three-phase equilibrium (PC = P).
According to the present analysis and despite the constancy of their global composition, slurries in gas-shortage do not behave like inert media, and the difference seems to be significant. Numerical modeling of slurries in gas shortage must account for the latent heats of hydrate decomposition and CO2 dissolution. This is especially true at the entrance of heat exchangers.
Section 3.2 mentions that gas shortage is also created when cooling a slurry separated from its gas phase. This is exactly the reverse operation of that described above. Consequently, cooling a slurry in gas shortage, e.g. within the slurry bath in a hydrate crystallizer, also involves changes in compositions according to equation (11), and the corresponding sensible and latent contributions to enthalpy changes.
Once again, only equilibrium states are considered herein. They are sufficient for describing a paradoxical behavior of slurries in gas shortage (involvement of latent heat although no gas is supplied nor withdrawn). Adding kinetic effects to the analysis could be a continuation of the present study, where the rates of hydrate decomposition and CO2 dissolution would be related to deviations from equilibrium.
4.5 Validation
It would be worth validating the present analysis of slurries in gas shortage with experimental data. However, experimental works on hydrate-forming systems focus attention on how hydrates form or decompose, to evaluate the amount of hydrate, the reaction rate, the latent heat, or the process reproducibility. In all of those experiments, it is ensured that enough gas is supplied to the system because gas unavailability would create a bias in measurements. To the author’s knowledge, there is no experimental data on slurries in gas shortage to which the present results could be compared. Nevertheless, the phenomenon described above could be tested experimentally. The experimental set-up would consist of a loop with (1) a storage tank filled with a slurry of mixed hydrate, (2) a mechanical pump that will extract a slurry flow from the tank and significantly compress it, (3) a small heating section where the heat flux transmitted to the slurry flow would be monitored together with temperature at the inlet and at the outlet of the heating section; the transmitted heat flux should be small enough for the slurry to remain in gas-shortage (i.e. with PC < P, even at the outlet of the heating section), and (4) a diaphragm producing a significant pressure drop before returning to the tank. Interpretation of measurements would relate the heat flux and the temperature jump, in order to detect whether heating only involves sensible heat, or also latent heat as predicted herein.
5 Conclusion
Mixed-hydrate slurries consist of crystals of gas-hydrates in suspension in a salt solution. When separated from their gas phase, such slurries depart from the three-phase equilibrium: they are in gas shortage. Equilibria in gas shortage are represented in a two-fold phase diagram that displays solid–liquid and liquid domains. Based on equality between the chemical potentials of CO2 molecules in either phase, the present analysis introduces the notion of gas partial pressure. It also predicts mass transfers between the liquid and solid phases. When used in secondary refrigeration circuits, slurries in gas shortage may behave differently from slurries in equilibrium with a gas phase, a feature to include in numerical simulations. The article proposes an experimental approach for testing whether the present analysis corresponds to reality.
Lastly, it is worth noting that many other gas-hydrate-forming systems can experience gas-shortage: systems with another salt, like Tetra-n-Butyl-Ammonium Bromide (TBAB) or Tetrahydrofuran (THF), including binary systems without salt and forming single gas-hydrates, plus systems with another gas that can also form hydrates and dissolve into water, e.g. CH4.
Conflict of interest
Authors declare no conflict of interest.
Acknowledgments
This work was done in the framework of the GDR2026 “Hydrates de gaz” (Gas-Hydrates).
References
- Cowan D., Gartshore J., Chaer I., Francis C., Maidment G. (2010) REAL zero – reducing refrigerant emissions and leakage – feedback from the IOR project, in: Proc. Inst. R. 2009-10, 7, IOR The Institute Of Refrigeration, 16 p. [Google Scholar]
- Fournaison L., Delahaye A., Chatti I., Petitet J.P. (2004) CO2 hydrates in refrigeration processes, Ind. Eng. Chem. Res. 43, 20, 6521–6526. [CrossRef] [Google Scholar]
- Mota-Babiloni A., Navarro-Esbri J., Barragan-Cervera A., Moles F., Peris B., Verdu G. (2015) Commercial refrigeration – an overview of current status, Int. J. Refrig.-Rev. Int. Froid. 57, 186–196. [CrossRef] [Google Scholar]
- Wang K., Eisele M., Hwang Y., Radermacher R. (2010) Review of secondary loop refrigeration systems, Int. J. Refrig.-Rev. Int. Froid. 33, 2, 212–234. [CrossRef] [Google Scholar]
- Compingt A., Blanc P., Quidort A. (2009) Slurry for refrigeration industrial kitchen application, in 8th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, M. Kauffeld (ed), Int. Inst. Refrigeration IIR-IIF, Karlsruhe, Germany, pp. 135–144. [Google Scholar]
- Gschwander S., Schossig P. (2009) Phase change slurries as heat transfer and storage fluids for cooling applications, in 8th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, M. Kauffeld (ed), Int. Inst. Refrigeration IIR-IIF, Karlsruhe, Germany, pp. 82–89. [Google Scholar]
- Sloan E.D., Koh C.A. (2008) Clathrate hydrates of natural gases, Third Edition Preface, CRC Press-Taylor & Francis Group, Boca Raton, FL. [Google Scholar]
- Ilani-Kashkouli P., Mohammadi A.H., Naidoo P., Ramjugernath D. (2016) Hydrate phase equilibria for CO2, CH4, or N2 + tetrabutylphosphonium bromide (TBPB) aqueous solution, Fluid Phase Equilib. 411, 88–92. [CrossRef] [Google Scholar]
- Lin W., Dalmazzone D., Fuerst W., Delahaye A., Fournaison L., Clain P. (2014) Thermodynamic properties of semiclathrate hydrates formed from the TBAB plus TBPB plus water and CO2 + TBAB + TBPB plus water systems, Fluid Phase Equilib. 372, 63–68. [CrossRef] [Google Scholar]
- Mayoufi N., Dalmazzone D., Delahaye A., Clain P., Fournaison L., Fuerst W. (2011) Experimental data on phase behavior of simple Tetrabutylphosphonium Bromide (TBPB) and mixed CO2 + TBPB semiclathrate hydrates, J. Chem. Eng. Data 56, 6, 2987–2993. [CrossRef] [Google Scholar]
- Shi L.-L., Liang D.-Q., Li D.-L. (2013) Phase equilibrium data of tetrabutylphosphonium bromide plus carbon dioxide or nitrogen semiclathrate hydrates, J. Chem. Eng. Data 58, 7, 2125–2130. [CrossRef] [Google Scholar]
- Zhang P., Ye N., Zhu H., Xiao X. (2013) Hydrate equilibrium conditions of tetra-n-butylphosphonium bromide + carbon dioxide and the crystal morphologies, J. Chem. Eng. Data 58, 6, 1781–1786. [CrossRef] [Google Scholar]
- Chami N., Bendjenni S., Clain P., Osswald V., Delahaye A., Fournaison L., Dalmazzone D. (2021) Thermodynamic characterization of mixed gas hydrates in the presence of cyclopentane as guest molecule for an application in secondary refrigeration, Chem. Eng. Sci. 244, 10. [Google Scholar]
- Lv Y., Xia X.R., Wang F., Wu X.D., Cheng C.X., Zhang L.X., Yang L., Zhao J.F., Song Y.C. (2022) Clathrate hydrate for phase change cold storage: Simulation advances and potential applications, J. Energy Storage 55, 20. [Google Scholar]
- Pahlavanzadeh H., Eslamimanesh A., Ghavi A. (2022) Gas hydrate phase equilibrium data for the CO2 + TBPB + THF plus water system, J. Chem. Eng. Data 67, 9, 2792–2799. [CrossRef] [Google Scholar]
- Bi Y.H., Guo T.W., Zhang L., Zhang H., Chen L.G. (2009) Experimental study on cool release process of gas-hydrate with additives, Energy Build. 41, 1, 120–124. [CrossRef] [Google Scholar]
- Shi L., Yi L., Shen X., Wu W., Liang D. (2017) The effect of tetrabutylphosphonium bromide on the formation process of CO2 hydrates, J. Mol. Liq. 229, 98–105. [CrossRef] [Google Scholar]
- La Sala J. (2009) Froid indirect pratique – fluides frigoporteurs liquides, Tethila Ed. [Google Scholar]
- Dufour T., Oignet J., Ben Abdallah R., Hoang H.M., Leducq D., Delahaye A., Fournaison L., Pons M. (2016) Dynamic modelling of secondary refrigeration loop with CO2 hydrate slurry, in 11th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, M. Kauffeld (ed), International Institute of Refrigeration, Paris, pp. 181–188. [Google Scholar]
- Youssef Z., Fournaison L., Delahaye A., Pons M. (2019) Management of vapor release in secondary refrigeration processes based on hydrates involving CO2 as guest molecule, Int. J. Refrig.-Rev. Int. Froid. 98, 202–210. [CrossRef] [Google Scholar]
- Lv X.F., Yu D., Li W.Q., Shi B.H., Gong J., Asme (2013) Experimental study on blockage of gas hydrate slurry in a flow loop, In Proceedings of the 9th International Pipeline Conference – 2012, Vol. 4, American Society of Mechanical Engineers, Calgary, Alberta, Canada, pp. 37–43. [Google Scholar]
- Balakin B.V., Hoffmann A.C., Kosinski P. (2011) Experimental study and computational fluid dynamics modeling of deposition of hydrate particles in a pipeline with turbulent water flow, Chem. Eng. Sci. 66, 4, 755–765. [Google Scholar]
- Dufour T., Hoang H.M., Oignet J., Osswald V., Clain P., Fournaison L., Delahaye A. (2017) Impact of pressure on the dynamic behavior of CO2 hydrate slurry in a stirred tank reactor applied to cold thermal energy storage, Appl. Energy 204, 641–652. [CrossRef] [Google Scholar]
- Diamond L.W., Akinfiev N.N. (2003) Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: evaluation of literature data and thermodynamic modelling, Fluid Phase Equilib. 208, 1–2, 265–290. [CrossRef] [Google Scholar]
- Lv X.F., Shi B.H., Wang Y., Gong J. (2013) Study on gas hydrate formation and hydrate slurry flow in a multiphase transportation system, Energy Fuels 27, 12, 7294–7302. [CrossRef] [Google Scholar]
- Pons M., Hoang H.-M., Dufour T., Delahaye A., Fournaison L. (2018) Energy analysis of two-phase secondary refrigeration in steady-state operation, Part 1: global optimization and leading parameter, Energy 161, 1282–1290. [CrossRef] [Google Scholar]
- IIF-IIR (2003) R744 CO2 dioxyde de carbone : Propriétés thermophysiques, IIF-IIR, Paris. [Google Scholar]
- Alexander D.M., Hill D.J.T., White L.R. (1971) Evaluation of thermodynamic functions from aqueous solubility measurements, Aust. J. Chem. 24, 6, 1143. [CrossRef] [Google Scholar]
- Koschel D., Coxam J.Y., Rodier L., Majer V. (2006) Enthalpy and solubility data of CO2 in water and NaCl(aq) at conditions of interest for geological sequestration, Fluid Phase Equilib. 247, 1–2, 107–120. [CrossRef] [Google Scholar]
- Barbero J.A., Hepler L.G., McCurdy K.G., Tremaine P.R. (1983) Thermodynamics of aqueous carbon-dioxide and sulfur-dioxide – heat-capacities, volumes, and the temperature-dependence of ionization, Can. J. Chem. 61, 11, 2509–2519. [CrossRef] [Google Scholar]
- Hnedkovsky L., Wood R.H. (1997) Apparent molar heat capacities of aqueous solutions of CH4, CO2, H2S, and NH3 at temperatures from 304 K to 704 K at a pressure of 28 MPa, J. Chem. Thermodyn. 29, 7, 731–747. [CrossRef] [Google Scholar]
- Span R., Wagner W. (1996) A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa, J. Phys. Chem. Ref. Data 25, 6, 1509–1596. [Google Scholar]
Appendix
Equations of state and thermophysical properties in the ternary system H2O + TBPB + CO2
This Appendix just provides a brief summary of the values or simplified correlations used in the computations: π = P/P1 is the non-dimensionalized pressure (with P1 = 1 MPa) and the temperature T is in Celsius.
Equations of state
The equation of state for the hydrate-formation equilibrium was adjusted on the experimental data of refs. [8, 10–12]: ![$$ f{T}_{\mathrm{eq}}\left(P,x\right)=B/\left[A(x)-\mathrm{Ln}\left(P/{P}_1\right)\right]-273.15 $$](/articles/stet/full_html/2023/01/stet20220168/stet20220168-eq15.gif) (A.1)with B = 24520 and A(x) = 85.49 + 60.85 · δx
2.328 · (1 – 8.067 · δx + 27.55 · δx
2) where δx = 0.3 − x.
(A.1)with B = 24520 and A(x) = 85.49 + 60.85 · δx
2.328 · (1 – 8.067 · δx + 27.55 · δx
2) where δx = 0.3 − x.
For CO2-solubility in aqueous solutions, the function was adjusted on the data of ref. [24]: 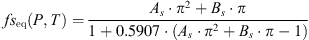 (A.2)with
(A.2)with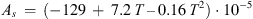 (A.3)and
(A.3)and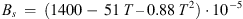 (A.4)
(A.4)
The van der Waals equation is used as a state equation for gaseous carbon dioxide (non-ideal):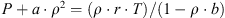 (A.5)
(A.5)
The best adjustment to the data of ref. [27] in the domain [0.5-5 MPa] and [0-50 °C] is obtained with a = 272.525 Pa·m6·kg−2 and b = 1.88406 × 10−3 m3·kg−1. With a density of the order of 10 kg·m−3 (value at 0.5 MPa and 10 °C [27]), the gas phase is significantly lighter than the other phases: the density of the hydrate crystals is 1200 kg·m−3 and that of the liquid solution is 1000–1050 kg·m−3.
The mass fractions of TBPB and CO2 in the mixed-hydrate crystal are respectively: YA = 0.342 and YC = 0.071 [12].
Thermophysical properties
From the thermal point of view, hydrate crystallization and gas dissolution are exothermal. The latent heat of crystallization of the mixed-hydrate is about two-thirds that of ice: ΔHS = -200 kJ (kg_hydrate)−1 [11, 12]. When referring to the amount of dissolved CO2, the latent heat of dissolution is not negligible: ΔHCL = -340 kJ (kg_dissolved_CO2)−1 [28, 29].
For the condensed phases, there is no difference between cp and cv. The values used herein are 2685 J kg−1·K−1 for the hydrate, around 3900 J kg−1·K−1 for the TBPB solution, and 5500 J kg−1·K−1 for the dissolved CO2 [30, 31]. The specific heat at constant volume cv of gaseous CO2 was adjusted to the data of ref. [32] in the domain of interest; the resulting phenomenological function is: cνG = C0 + C1 · π + C4 · π 4, with C0 = 541 + 0.98 T, C1 = 37.2 exp(−0.01277 T), and C4 = 0.715 exp(−0.07 T), all in J kg−1·K−1.
Tabulated data
The main data displayed in Figures 4 and 5 are presented in the following tables
| Data for P = 0.5 MPa and x0 = 0.20 | χC | T [°C] | h [kJ·kg-1] |
| Central point | 8.9 × 10−3 | 10.9 | 7.4 |
| End of the 0L line | 0.1 × 10−3 | 7.5 | −2.8 |
| End of the SL0 line | 19.8 × 10−3 | 10.6 | −28.2 |
| End of the 0LG line | 20.0 × 10−3 | 10.9 | 7.3 |
| End of the L0 line | 7.5 × 10−3 | 16.5 | 29.4 |
| Data for P = 0.3 MPa and x0 = 0.20 | χC | T [°C] | h [kJ·kg−1] |
|---|---|---|---|
| Central point | 5.7 × 10−3 | 9.6 | 3.5 |
| End of the 0L line | 0.06 × 10−3 | 7.5 | −2.8 |
| End of the SL0 line | 19.8 × 10−3 | 9.1 | −41.4 |
| End of the 0LG line | 20.0 × 10−3 | 9.6 | 3.4 |
| End of the L0 line | 4.65 × 10−3 | 16.0 | 28.3 |
| Data for P = 0.5 MPa and x0 = 0.15 | χC | T [°C] | h [kJ·kg-1] |
| Central point | 9.6 × 10−3 | 10.3 | 7.6 |
| End of the 0L line | 0.1 × 10−3 | 6.8 | −2.8 |
| End of the SL0 line | 19.7 × 10−3 | 9.0 | −28.4 |
| End of the 0LG line | 20.0 × 10−3 | 10.3 | 7.5 |
| End of the L0 line | 8.2 × 10−3 | 15.5 | 28.5 |
All Tables
Heat quantities involved in the four compression processes displayed in Figure 3, in kJ for a system containing 1 kg of water, 275 g of TBPB plus as much gas as required in the gas phase. Initially, the system contains 100 g of hydrate crystals. Both hydrate decomposition and CO2 dissolution involve latent heat. Values are negative for exothermal phenomena.
Thermal effects when heating a slurry, initially in gas-shortage by mechanical compression (P = 0.5 MPa and PC = 0.4 MPa), until it reaches three-phase equilibrium (PC = P).
All Figures
 |
Figure 1 Process diagram of a secondary refrigeration circuit. 1–2: storage tanks (slurry plus gas); 3: distribution loop; 4: main pump; 5–6–7: cold supply devices for each end-user, resp. valve & pump, heat exchanger and cyclone; 8–9–10: control valve, compressor, and heat exchanger (see more details in ref. [20]); G: Gas phase; SL: Slurry (solid + liquid). |
| In the text | |
 |
Figure 2 Reactor for generating gas-hydrate from a stirred three-phase system, slurry (SL) + gas (G), or for compressing it. The valve located on the lid can be used for adding gas into the reactor; the system temperature is controlled by the double-jacket heat exchanger (HX). |
| In the text | |
 |
Figure 3 Phase diagrams with equilibrium curves (dashed lines) for the system with mixed-hydrate of TBPB + CO2. A: [T-x] diagram with two 0LG curves (liquid solutions in equilibrium with both solid crystals and gaseous CO2) at 0.5 and 0.3 MPa. B: [P-T] diagram with four equidistant values of x. Solid arrows: four processes for compressing the three-phase system from 0.3 to 0.5 MPa: LV = isochoric; LX = isosteric; LA = adiabatic; LT = isothermal. |
| In the text | |
 |
Figure 4 Phase diagram for slurries in gas-shortage, at 0.5 MPa and with x0 = 0.20. Two graphs: A [T-χC] and B [h-χC]. Notations: S = Solid; L = Liquid; G = gas. The partial pressure PC is constant (0.4 MPa) along the dashed curves. |
| In the text | |
 |
Figure 5 Respective influences of either the total pressure P or the global additive concentration x0, on the phase diagram of Figure 4. Same graphs, notations, and solid lines as in Figure 4. Short dashes “ P ”: P = 0.3 MPa, x0 = 0.20; long dashes “ x 0”: x0 = 0.15, P = 0.5 MPa. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




