| Issue |
Sci. Tech. Energ. Transition
Volume 78, 2023
Characterization and Modeling of the Subsurface in the Context of Ecological Transition
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.2516/stet/2023004 | |
| Published online | 12 April 2023 | |
Regular Article
Hydrogen and air storage in salt caverns: a thermodynamic model for phase equilibrium calculations
1
IFP Energies Nouvelles, 1 et 4 Avenue de Bois-Préau, 92852 Rueil-Malmaison Cedex, France
2
GEOSTOCK, 2 Rue des Martinets, 92500 Rueil-Malmaison Cedex, France
* Corresponding author: nicolas.ferrando@ifp.fr
Received:
16
September
2022
Accepted:
24
February
2023
When storing gas in a salt cavern, it occupies most of the excavated volume, but the lower part of the cavern inevitably contains residual brine, in contact with the gas. The design of hydrogen and compressed air storage in salt caverns requires to have a thermodynamic model able to accurately predict both phase properties such as densities, and phase equilibrium (gas solubility and water content of the vapour phase). This work proposes a parameterization of the e-PPC-SAFT equation of state in this context. Experimental data of pure components and mixtures of light gas + pure water and light gas + salted water are reviewed and used to fit pure component parameters for hydrogen, nitrogen, oxygen, and the brine, and binary interaction parameters between H2, O2, N2 + water and H2, O2, N2 + ions (Na+ and Cl−), for temperature ranging from 273 to 473 K and salinities up to NaCl saturation (6 mol/kg). The model developed delivers good accuracy in reproducing data: the average deviation between experiments and calculated data is between 3% and 9% for gas solubility in saturated brine. More interestingly, the model has been validated on its capability to predict data not included in the parameterization database, including the composition of the vapor phase, and its extension to a mixture, such as air. Finally, it has been used in a case study of Compressed Air Energy Storage (CAES) to evaluate the water content of the gas produced during injection-withdrawing cycles.
Key words: Thermodynamic model / SAFT / Hydrogen / Air / Salt cavern
© The Author(s), published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the context of the energy transition, renewable energies like solar and wind are promising solutions to replace fossil fuels [1]. However, such kind of energy production is intermittent. To overcome this issue, these renewable energies can be stored during high-energy production phases, and used when needed [2]. Among all storage technologies, underground storage is well known and provides several advantages such as safety, longevity, and high storage capacity [3]. More specifically, storage in salt caverns is very promising for light gas storage due to very low permeability. The electricity produced from renewables must first be turned into an energy carrier that can be stored, like reactive hydrogen [4], or be used for Compressed Air Energy Storage (CAES) [5].
Salt caverns are developed by injecting water into a geological salt deposit, thus leaching the salt and then withdrawing the brine. Once the desired geometrical volume is obtained, the first gas fill is made by injecting gas and withdrawing the brine. At the end of this so-called “debrining” stage, an amount of brine typically between 1.000 m3 and 10.000 m3 stay at the bottom of the cavern. The cavern is then put into operation. This presence of the residual brine impacts the gas storage operations. First, it can solubilize a part of the injected gas. Second, while it is injected dry, the gas produced contains a higher amount of water, making it necessary to use dehydration surface processes. In the case of compressed air, the withdrawn humid air causes aggressive corrosion conditions for the well and surface piping and equipment. It is thus of primary importance to have a thermodynamic model able to predict phase equilibrium between brine and gas in large conditions of temperature and pressure, and up to saturation in terms of salinity.
Concerning the phase equilibrium model between hydrogen and brines, only a few thermodynamic models have been published. Lopez-Lazaro et al. [6] proposed an approach based on the Soreide and Whitson equation of state [7] calibrated on a few existing experimental and molecular simulation data. Recently, Chabab et al. [8] published new experimental data in temperature and salinity ranges in better accordance with underground storage, and they used both Soreide and Whitson and an electrolyte version of the Cubic Plus Association equation of state [9] to successfully model their data. Li et al. [10] proposed a heterogeneous approach based on the Pitzer activity model and Henry constants for the aqueous phase and a pure-hydrogen equation of state for the vapour phase. This model assumes that the vapour phase behaves ideally, which leads to non-negligible deviations at high pressure, as demonstrated in a previous study [11]. Recently, Zhu et al. [12] also proposed a heterogeneous approach using a Pitzer model for the liquid phase. The fugacity of hydrogen in the vapour phase is calculated with a pure-hydrogen model. A correction is brought to evaluate the water content in this phase. Although accurate on data used for model calibration, these heterogeneous approaches of Li et al. and Zhu et al. are rather devoted to low-pressure conditions and do not allow an accurate calculation of the vapour phase composition. Another heterogeneous approach was recently proposed by Torín-Ollarves and Trusler, based on the Setchenow coefficient and Henry constant correlations [13]. This model fits well with experimental data but remains quite empirical with a large number of parameters. Again, this model does not allow an accurate calculation of the vapour phase composition. Roa Pinto et al. proposed to use an electrolyte version of the PPC-SAFT equation of state and show good agreement with previous models, but also a good capacity in extrapolation when compared to data not used in the calibration database [11]. However, this model exhibits non-negligible deviations in the compressibility factor of pure hydrogen at high pressure, opening the way to improvements to get better accuracy of gas volume produced during storage withdrawal.
Concerning phase equilibrium between air and saturated brines, no specific model has been found in the literature probably due to the lack of experimental data, although molecular simulation is more and more used as a complementary tool to experiments in this field [14]. Nevertheless, we can mention the modeling work recently proposed by Chabab et al. on N2 + brine and O2 + brine systems with the Soreide and Whitson equation of state [15]. This model has been validated on both gas solubility and water content in the vapor phase at a large range of temperatures and salinities. Coupled with their previous parameterization for other gases like H2, CO2, and CH4, this is probably today the most complete thermodynamic model to deal with gas storage in salt caverns.
In this work, we propose a thermodynamic model able to predict both phase equilibrium: H2 + brine and Air + brine. Air is considered a mixture of 80% mol. of nitrogen and 20% mol. of oxygen. Thus, binary systems N2 + brine and O2 + brine must be studied first, before evaluating the model in prediction on the multi-component mixture air + brine. Brine is assumed to be made of water and NaCl since this salt is the most abundant in salt caverns. The model proposed is a revision of the initial model of Roa Pinto et al. [11]. It is based on the e-PPC-SAFT equation of state: due to its strong physical background, this model has a good capability of extrapolation, which is an important requirement in the present case of scarce experimental data. This model will be parameterized to reproduce not only gas solubility in brine but also the composition of the vapor phase. The capability of the model to predict accurately the water content of the vapor phase is a key benefit compared to existing modeling works based on a heterogeneous approach [10, 12, 13]. Furthermore, the accuracy of a SAFT-based thermodynamic model, which includes specific terms to deal with association and electrolyte interactions, is expected to be at least the same as a cubic-based model such as the Soreide and Whitson equation of state, and to have better predictive behavior. Another key benefit of the model proposed in this work is to be based on an ion-parameterization approach, and not a salt-parameterization approach like with the Soreide and Whitson approach. Consequently, such a model allows calculating specifically the liquid fugacity of each ion individually, which can be of prior importance if this model has to be further used in a reactive equilibria scheme where ions are involved, for instance in typical fluid-rock interaction calculations.
In the first part of this article, the e-PPC-SAFT framework will be recalled, with a specific focus on the model parameters. In the second part, a review of available experimental data is proposed. The systems investigated cover pure components (hydrogen, nitrogen, oxygen), brine, and mixtures of light gases with pure water and brine. Then, in the third part, the model parameterization is carried out for both pure components and mixtures. In the fourth part, the model is validated on its capability to predict data and properties not used in the parameterization database, and on its capability to compute multicomponent mixtures such as air only from binary considerations. Finally, an application of this model will be presented to calculate gas moisture during typical Compressed Air Energy Storage injection-withdrawal cycles.
2 The e-PPC-SAFT model
The e-PPC-SAFT equation of state [16] is used to model the different forces acting in an electrolytic multiphasic system. It gives the reduced residual Helmholtz energy A
res as a sum of different contributions, each contribution representing a specific interacting force between particles: (1)where R is the ideal gas constant and T the temperature.
(1)where R is the ideal gas constant and T the temperature.
The first four contributions (hard-sphere, chain, dispersion, and association) derive directly from the original PC-SAFT version of Gross and Sadowski [17]. The hard sphere term describes the repulsive interactions between hard spheres. Its expression is the following:![$$ \frac{{A}^{\mathrm{hs}}}{{RT}}=\frac{6}{{\rho \pi }}\left[\left(\frac{{\xi }_2^3}{{\xi }_3^2}-{\xi }_0\right)\mathrm{ln}\left(1-{\xi }_3\right)+\frac{{3\xi }_1{\xi }_2}{1-{\xi }_3}+\frac{{\xi }_2^3}{{\xi }_3{\left(1-{\xi }_3\right)}^2}\right] $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq2.gif) (2)with
(2)with![$$ {\xi }_k=\frac{\pi {N}_{\mathrm{A}}\rho }{6}{\sum }_{i=1}^n{x}_i{m}_i{\left({d}_i(T)\right)}^k\enspace \hspace{1em}\mathrm{and}\hspace{1em}{d}_i(T)={\sigma }_i^{\mathrm{HS}}\enspace \left[1-{\lambda }_i{e}^{-3\frac{{\epsilon }_i}{{kT}}}\right], $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq3.gif) (3)where, ρ is the molar density and total volume of the fluid, NA the Avogadro’s number (6.02214 × 1023 mol−1),
(3)where, ρ is the molar density and total volume of the fluid, NA the Avogadro’s number (6.02214 × 1023 mol−1),  is the hard sphere diameter, ε
i
is the dispersive energy parameter, λ is the softness parameter which is equal to 0.12 (except for water in the model used in this work: λ
i
= 0.203) and x
i
is the molar fraction of component i.
is the hard sphere diameter, ε
i
is the dispersive energy parameter, λ is the softness parameter which is equal to 0.12 (except for water in the model used in this work: λ
i
= 0.203) and x
i
is the molar fraction of component i.
The chain term is used to model the chain formation between segments. This contribution is given by: (4)where m
i
is the chain length parameter and
(4)where m
i
is the chain length parameter and 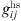 is the radial distribution function given by Boublik [18] and Mansoori et al. [19]:
is the radial distribution function given by Boublik [18] and Mansoori et al. [19]: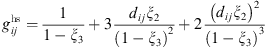 (5)and
(5)and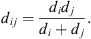 (6)
(6)
The dispersive contribution describes the short-range Van der Waals attraction between segments. The corresponding expression is: (7)with
(7)with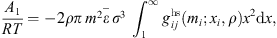 (8)
(8)
![$$ \frac{{A}_2}{{RT}}=-{\rho \pi m}{\left({Z}^{\mathrm{hs}}+\rho \frac{\partial {Z}^{\mathrm{hs}}}{{\partial \rho }}\right)}^{-1}\enspace \overline{{m}^2{\epsilon }^2\enspace {\sigma }^3}\enspace \frac{\partial }{{\partial \rho }}\left[\rho {\int }_1^{\mathrm{\infty }}{g}_{{ij}}^{\mathrm{hs}}({m}_i;{x}_i,\rho ){x}^2\mathrm{d}x\right], $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq11.gif) (9)where
(9)where 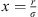 is the reduced radial distance around a segment and Z
hc is the compressibility factor of hard chain. Mixing parameters
is the reduced radial distance around a segment and Z
hc is the compressibility factor of hard chain. Mixing parameters 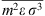 and
and 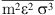 are given by:
are given by: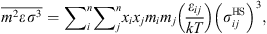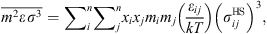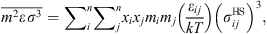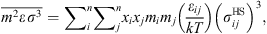 (10)
(10)
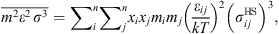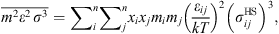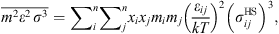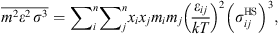 (11)where ε
ij
and
(11)where ε
ij
and 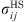 are evaluated using the Lorentz–Berthelot mixing rules:
are evaluated using the Lorentz–Berthelot mixing rules: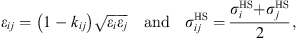 (12)where k
ij
is an empirical interaction binary parameter.
(12)where k
ij
is an empirical interaction binary parameter.
The association term describes the strong short-range attractions due to association forces between association sites. It derives from the Wertheim theory [20] and is given by [21]:![$$ \frac{{A}^{\mathrm{association}}}{{RT}}={\sum }_i{n}_i{\sum }_{{A}_i}\left[\left(\mathrm{ln}{X}^{{A}_i}-\frac{{X}^{{A}_i}}{2}\right)+\frac{1}{2}{M}_i\right]\enspace $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq19.gif) (13)with
(13)with![$$ {X}^{{A}_i}={\left[1+{N}_{\mathrm{A}v}{\sum }_{{B}_j}\left(\rho {X}^{{A}_j}{\Delta }^{{A}_i{B}_j}\right)\right]}^{-1} $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq20.gif) (14)and
(14)and![$$ {\Delta }^{{A}_i{B}_j}={g}_{{ij}}^{\mathrm{hs}}\left({d}_{{ij}}\right){{d}_{{ij}}}^3\left[\mathrm{exp}\left(\frac{{\epsilon }^{{A}_i{B}_j}}{{kT}}\right)-1\right]{{d}_{{ij}}}^3{k}^{{A}_i{B}_j}. $$](/articles/stet/full_html/2023/01/stet20220153/stet20220153-eq21.gif) (15)
(15)
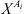 is the fraction of association sites non-bonded to site A of molecule i. M
i
is the number of association sites in molecule i, and
is the fraction of association sites non-bonded to site A of molecule i. M
i
is the number of association sites in molecule i, and 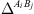 the association force between site A of molecule i and site B of molecule j. It is characterized by two binary parameters: the association energy (
the association force between site A of molecule i and site B of molecule j. It is characterized by two binary parameters: the association energy (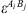 ) and is the association volume (
) and is the association volume (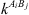 ), determined from the CR-1 mixing rule:
), determined from the CR-1 mixing rule: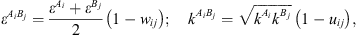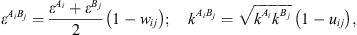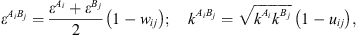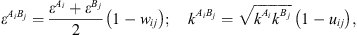 (16)where w
ij
and u
ij
are empirical interaction binary parameters.
(16)where w
ij
and u
ij
are empirical interaction binary parameters.
From this original version of the PC-SAFT equation of state, Nguyen-Huynh et al. [22] added a specific polar term from the Jog and Chapman theory [23] to include interactions between dipoles and quadrupoles. The expression of this term is the following: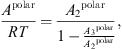 (17)
(17)
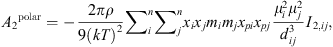 (18)
(18)
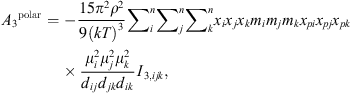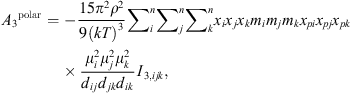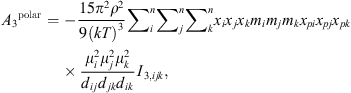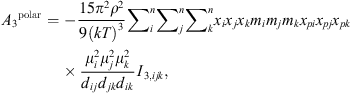 (19)where μ
i
is the dipole moment of the molecule and x
pi
its polar fraction.
(19)where μ
i
is the dipole moment of the molecule and x
pi
its polar fraction. 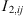 and
and 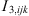 are correlations whose expressions can be found in [23]. The quadripolar moment Q
i
of the molecule and its quadrupolar fraction
are correlations whose expressions can be found in [23]. The quadripolar moment Q
i
of the molecule and its quadrupolar fraction 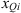 can also be taken into account, following equations given in [23].
can also be taken into account, following equations given in [23].
The addition of a Non-Additive Hard-Sphere (NAHS) term to the PPC-SAFT equation of state was proposed by Trinh et al. to improve prediction with hydrogen-containing mixtures [24] by correcting the additivity assumption of the hard spheres. The expression of this term is: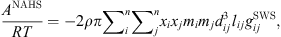 (20)where
(20)where 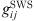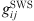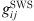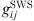 is the radial distribution function of square-well potential [25] and d
ij
the cross-diameter calculated by:
is the radial distribution function of square-well potential [25] and d
ij
the cross-diameter calculated by: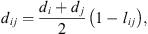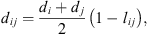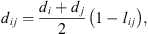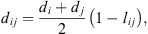 (21)where l
ij
is an empirical binary interaction parameter.
(21)where l
ij
is an empirical binary interaction parameter.
The last two terms of equation (1) are specific to electrolytic systems. For long-range electrolytic interactions, the use of MSA (Mean Spherical Approximation) is used as suggested by many authors [11, 16, 26–32], although an approach based on Debye–Hückel theory is expected to give a similar performance [33]. Its expression is given by: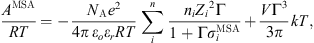 (22)where ε
r
is the dielectric constant of the solution, ε
o the dielectric constant in the vacuum (8.85418 × 10−12 C mol−1), n
i
the number of moles of ion i, e is the electron charge (1.60218 × 10−19 C), Z
i
the ion charge,
(22)where ε
r
is the dielectric constant of the solution, ε
o the dielectric constant in the vacuum (8.85418 × 10−12 C mol−1), n
i
the number of moles of ion i, e is the electron charge (1.60218 × 10−19 C), Z
i
the ion charge, 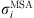 the solvated ion diameter and Γ the shielding parameter calculated as follows:
the solvated ion diameter and Γ the shielding parameter calculated as follows: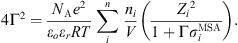 (23)
(23)
In equation (1), the Born term is also classically used to model short-range ion solvation forces [11, 16, 27]. It is defined by: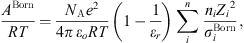 (24)where
(24)where 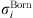 is the Born diameter for each ion. This diameter is determined from experimental Gibbs energies of solvation
is the Born diameter for each ion. This diameter is determined from experimental Gibbs energies of solvation  [34], through the equation resulting from equation (25):
[34], through the equation resulting from equation (25):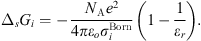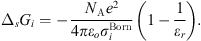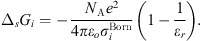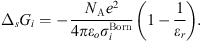 (25)
(25)
Both MSA and Born terms involve the dielectric constant of the aqueous solution. In this work, it is calculated using the model of the dielectric constant of pure water proposed by Schreckenberg et al. [27] to which the salt correction of Pottel is added [35]: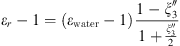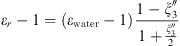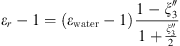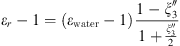 (26)with
(26)with (27)where N
T
is the total number of moles, V is the volume of the system, d
v
and d
T
are constants with a value for the water of 0.3777 dm3/mol and 1403 K respectively, and
(27)where N
T
is the total number of moles, V is the volume of the system, d
v
and d
T
are constants with a value for the water of 0.3777 dm3/mol and 1403 K respectively, and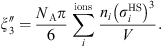 (28)
(28)
Finally, Table 1 provides a summary of what parameters are used for each term of the e-PPC-SAFT model.
e-PPC-SAFT pure-component and binary parameters.
Knowing the residual Helmholtz energy from equation (1), the fugacity coefficient 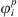 of each component i in a given phase p can be calculated from:
of each component i in a given phase p can be calculated from: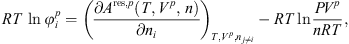 (29)where Vp
is the volume of the phase p,
(29)where Vp
is the volume of the phase p, 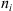 is the number of mole of component i, P is the pressure and n is the total mole number in phase p.
is the number of mole of component i, P is the pressure and n is the total mole number in phase p.
For all component i, phase equilibrium is calculated by equalizing fugacities of i in liquid and vapor phases, under mass balance constraint: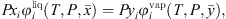 (30)where x and y stand for the liquid and vapor molar fraction, respectively, and
(30)where x and y stand for the liquid and vapor molar fraction, respectively, and 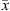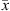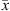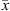 and
and 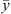 the vectors of compositions of these phases.
the vectors of compositions of these phases.
For light gases showing a very low solubility in the aqueous phase, it is common to express solubility in terms of the Henry constant. It is defined as: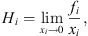 (31)where fi is the fugacity of i in the liquid or vapor phase. From an equation of state, it can be calculated by:
(31)where fi is the fugacity of i in the liquid or vapor phase. From an equation of state, it can be calculated by: (32)where
(32)where 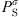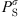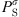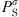 is the saturation pressure of the solvent, and the superscript
is the saturation pressure of the solvent, and the superscript  stands for infinite dilution of i in the solvent. It can be noticed that Henry’s constants computed with equation (32) are for real mixtures and not salt-free mixtures.
stands for infinite dilution of i in the solvent. It can be noticed that Henry’s constants computed with equation (32) are for real mixtures and not salt-free mixtures.
The computation of the Henry constant is carried out in two steps. First, a “bubble point” flash of the real solvent (i.e. with mole fraction including ions) is carried out. Then, the fugacity coefficient at infinite dilution for the gas is calculated in this real solvent. Other equilibria computed in this work (more specifically to plot pressure-composition and temperature-composition diagrams) are performed using a diphasic TP flash, always using the mole fractions of the real mixture, including ions. This flash algorithm equals the fugacity of all species (including ions) between liquid and vapor phases with respect to mass balance. It is worth noticing that the Born term used in the SAFT model makes the liquid fugacity coefficient of ions extremely low, resulting thus in a vapor composition very close to zero.
3 Review of experimental data
3.1 Pure components (H2, N2, O2)
In the context of underground gas storage, it is of primary importance for economic evaluations to calculate with very good accuracy the volume of the gas produced. Consequently, the parameterization of the light gases involved in this study (hydrogen, nitrogen, and oxygen) is carried out to reproduce experimental compressibility factors Z in temperature and pressure ranges of industrial interest: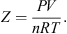 (33)
(33)
The compressibility factors of all these pure components are collected from the NIST database [36] for temperatures ranging from 273 to 473 K and pressures ranging from 1 to 300 bar.
3.2 Brine
The brine is considered to be an aqueous NaCl solution since halite is the most abundant salt found in salt caverns. NaCl is assumed fully dissociated in Na+ and Cl− ions. One of the most important properties to be correctly modeled is the Mean Ionic Activity Coefficient (MIAC) of NaCl salt since it describes the deviation from the ideality of the aqueous solution. MIAC is defined from a single ion activity coefficient by: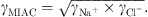 (34)
(34)
The e-PPC-SAFT equation of state computes fugacity coefficients φi, and not directly activity coefficients. The relationship between both for component i is: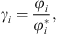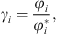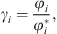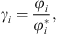 (35)where the exponent * is related to the reference state (infinite dilution for ions).
(35)where the exponent * is related to the reference state (infinite dilution for ions).
The MIAC experimental data covering a temperature range from 273 K to 473 K and salinities up to saturation are taken from [37]. Note that experimental ion activity coefficients are very often given in the molality scale, while the equation of state computes MIAC from equation (34) in the molar fraction scale. A conversion can be done using the molar fraction of the solvent: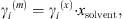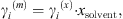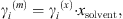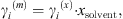 (36)where the exponents (m) and (x) stand for molality and molar fraction scale, respectively.
(36)where the exponents (m) and (x) stand for molality and molar fraction scale, respectively.
The composition of the gas produced during storage cycles is also of primary importance to designing surface facilities. More specifically, the water content of the vapor phase must be accurately known. Thus, special attention to our modeling is also paid to correctly reproduce the vapor pressure of the brine. Experimental data for this property on the same temperature and salinity ranges are taken from [38, 39]. Finally, a set of experimental brine densities [40] are also used to parameterize the model.
3.3 Light gas + pure water systems
Concerning hydrogen, Lopez-Lazaro et al. published recently a review of experimental hydrogen solubility in pure water data [6]: around 300 data from 273 to 623 K were collected and reconciliation in terms of Henry constants. These data were fitted following the empirical correlation suggested by Trinh et al. [41]: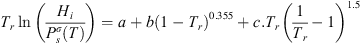 (37)where Tr is the reduced temperature of pure water (Tr = T/TC where TC is the critical temperature of pure water: 647 K).
(37)where Tr is the reduced temperature of pure water (Tr = T/TC where TC is the critical temperature of pure water: 647 K).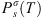 is the vapor pressure of the solvent, taken from the DIPPR database [42]. a, b, c are three empirical parameters given in Table 2.
is the vapor pressure of the solvent, taken from the DIPPR database [42]. a, b, c are three empirical parameters given in Table 2.
A similar review is proposed in this work for the solubility of nitrogen and oxygen in pure water. For both nitrogen and oxygen, experimental data are collected and converted in terms of the Henry constant. In the literature, the solubility data can be directly reported as Henry constant, or also in terms of Kuenen coefficient Si, Ostwald coefficient Li, Bunsen coefficient αi, and molar fraction as a function of temperature and pressure (“TPx” data). For this last kind of data, we retain here only data at low pressure, since conversion into Henry constant requires to be close to infinite dilution. The reference of experimental data collected is given in Table 3. The conversion rules in Henry constant recommended by IUPAC [43] are: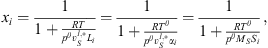 (38)where Tθ
and Pθ
are standard temperature (273.15 K) and pressure (1.013 bar),
(38)where Tθ
and Pθ
are standard temperature (273.15 K) and pressure (1.013 bar),  is the liquid molar volume of pure water at T, taken from the DIPPR databank, and MS the molar mass of pure water. From this molar fraction and equation (32), Henry constants are then estimated by:
is the liquid molar volume of pure water at T, taken from the DIPPR databank, and MS the molar mass of pure water. From this molar fraction and equation (32), Henry constants are then estimated by: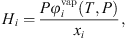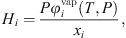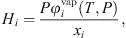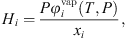 (39)where it is assumed that component i is pure in the vapor phase (composition of water is neglected), and
(39)where it is assumed that component i is pure in the vapor phase (composition of water is neglected), and  is the fugacity coefficient of pure component i at temperature T and pressure P calculated with e-PPC-SAFT model and parameters of Table 4. To check the assumption that water in the vapor phase is negligible, the pure water vapor pressure is calculated for each experimental data and compared to the experimental total pressure. It is found that on average, the pure water vapor pressure represents around 3% of the total pressure, which is less of the experimental uncertainty. This suggests that this assumption is valid.
is the fugacity coefficient of pure component i at temperature T and pressure P calculated with e-PPC-SAFT model and parameters of Table 4. To check the assumption that water in the vapor phase is negligible, the pure water vapor pressure is calculated for each experimental data and compared to the experimental total pressure. It is found that on average, the pure water vapor pressure represents around 3% of the total pressure, which is less of the experimental uncertainty. This suggests that this assumption is valid.
Experimental data used for model parameterization and model validation.
Pure component parameters in the e-PPC-SAFT model. Parameters in bold are those adjusted in this work. For O2, N2, and H2, parameters are adjusted on compressibility factors. For ions, parameters are adjusted on MIAC, brine vapor pressures, and brine densities.
The reconciliation experimental data are plotted in Figure 1. An average experimental uncertainty is estimated to be ±10%. These data are fitted using empirical equation (38) (bold line in Fig. 1). The parameters of this correlation are given in Table 2. Note that for O2, it can be observed that a few experimental data published are not consistent with most of the data. These inconsistent data have not been considered to establish the correlation.
 |
Fig. 1 Experimental Henry constants of N2 and O2 in pure water. Blue diamonds: from direct Henry constant data. Red squares: from Ostwald coefficient data. Green triangles: from Kuenen coefficient data. Purple crosses: from Bunsen coefficient data. Blue stars: from PTx data. The solid line is a fit of all data with correlation 38. The dotted lines are guides indicated ±10% from the correlation. |
3.4 Light gas + brine systems
Experimental hydrogen solubility data in saline water are relatively scarce in literature and cover only a limited range of temperature (up to 333 K) and salinities (2 mol/kg) [44–47]. Lopez-Lazaro et al. reviewed these data and proposed additional ones at higher temperatures (up to 500 K) from molecular simulations [6]. This set of solubility data converted into the Henry constant is used to parameterize our model. Very recently, Chabab et al. [8] and Torín-Ollarves and Trusler [13] published new solubility data for temperatures up to 423 K and salinities up to 5 mol/kg. These new data are used in this work as a validation dataset for the model.
In contrast to hydrogen, the experimental data of oxygen solubility in salted water cover a wider range of temperature (up to 473 K) and salinities (5.8 mol/kg) [48–51]. As indicated in Table 3, the recent experimental oxygen solubility data of Chabab et al. [52], not used in the parameterization database, will be used to validate the model.
Concerning nitrogen, experimental solubility data in saline water are very scarce in the literature. The published Henry constants (or data which can be converted in Henry constant following Eq. (39)) concern a very restricted temperature range (up to 298 K) [53, 54], and cannot be used alone to parameterize our model in an underground gas storage context. Thus, in contrast to other systems, the binary interaction parameter between N2 and ions is directly fitted to match “PTx” experimental data at elevated pressure, covering a wider range of temperature (303 to 398 K) and salinities (up to 5.5 mol/kg) [55, 56].
4 Model parameterization
4.1 Pure components (H2, N2, O2)
For hydrogen, nitrogen, and oxygen, the experimental compressibility factors are used to adjust the dispersion energy and segment diameter of each of these light gas, while segment numbers are taken from previous studies [92, 93]. Table 4 gives the optimized parameters, and Figure 2 compares calculated values and reference data.
 |
Fig. 2 Compressibility factor of H2, N2, and O2. Symbols: reference date from NIST database [36]. Lines: this model. |
The average deviations between model results and the reference data are equal to 0.1%, 0.2%, and 0.1% for hydrogen, nitrogen, and oxygen, respectively. These deviations are less than the uncertainties reported by the NIST for the reference data (0.2%, 0.5%, and 1.2%, respectively). The parameters fitted are consistent with other PC-SAFT parameter sets available in the literature [94–97].
4.2 Brine
For the brine (mixture of H2O, Na+, and Cl−), special attention should be paid to accurately reproduce MIAC close to NaCl saturation, since it corresponds to conditions encountered in salt caverns. It requires tuning not only pure ion parameters but also binary parameters between cation and anion since at high ionic concentration, ion pairing can be observed [98]. For pure ion parameters, we consider the hard sphere diameter equal to the Pauling diameter, and a segment number equal to 1.
In the e-PPC-SAFT framework, ions are assumed to interact with other particles only through association forces, and not through dispersion forces. Consequently, the energy dispersion parameter of ions is equal to 0. Finally, there are three parameters per ion to be adjusted: association energy, association volume, and MSA diameter. To better mimic ion-pairing formation at high salt concentration, the cross-binary parameters on association energy wij and association volume uij (Eq. (16)) between Na+ and Cl− are also adjusted. A total of seven parameters is then used for brine parameterization. The e-PPC-SAFT parameters of pure water are directly taken from a previous study [16]. Finally, the optimized parameters are reported in Table 4 (for pure component parameters), and on Table 5 (for binary parameters). Figure 3 compares experimental MIAC [37], vapor pressures [38, 39], and densities [40] with calculated values.
 |
Fig. 3 NaCl MIAC, vapor pressure, and density of NaCl aqueous solutions. Symbols: experimental data [37–40]. Lines: this model. |
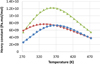 |
Fig. 4 Henry constant of H2 (diamonds), N2 (triangles), and O2 (circles) in pure water. Symbols: experimental data (Eq. (38)). Lines: this model. |
Summary of binary parameters adjusted in this work for the e-PPC-SAFT model.
A very good agreement is found in the whole range of temperatures and salinities. The average deviations between experimental and calculated MIAC, vapor pressures, and densities are equal to 2.0%, 1.3%, and 1.4%, respectively.
4.3 Light gas + pure water systems
Correlation 37 is used as reference data to adjust interaction binary parameters of the e-PPC-SAFT model between H2 and H2O, N2 and H2O, and O2 and H2O. This optimization is done for temperatures ranging from 273 to 473 K in order to focus on conditions of interest for gas underground storage. As mentioned in Table 1, two binary parameters can be tuned: the kij and lij parameters, involved in the cross energy dispersion and the cross diameter of the NAHS term, respectively. A previous study based on molecular simulations of the H2 + H2O system showed that the lij parameter has a stronger influence on Henry’s constant calculations [6]. Consequently, only this binary parameter is adjusted, and the kij parameter is set to 0. A preliminary optimization using a constant value of the lij parameter led to important deviations between experimental and calculated values. Furthermore, the model was not able to reproduce the maximum in the Henry constant curves observed experimentally. Thus, it was decided to introduce a temperature dependency for this binary parameter: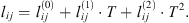 (4)
(4)
The adjusted 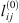 ,
, 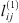 and
and 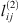 parameters are given in Table 5. It is highly recommended to use this correlation only in the subcritical domain (temperature less than 647 K) to avoid the too-large value of lij. Figure 3 presents the experimental data calculated data. This optimization leads to a good agreement, with an average deviation between 1.8%, 1.1%, and 1.3% for systems H2 + H2O, N2 + H2O, and O2 + H2O, respectively.
parameters are given in Table 5. It is highly recommended to use this correlation only in the subcritical domain (temperature less than 647 K) to avoid the too-large value of lij. Figure 3 presents the experimental data calculated data. This optimization leads to a good agreement, with an average deviation between 1.8%, 1.1%, and 1.3% for systems H2 + H2O, N2 + H2O, and O2 + H2O, respectively.
4.4 Light gas + brine systems
In the e-PPC-SAFT model, ions are assumed to interact with solvent and neutral solutes only through repulsive and associative forces (no dispersion interaction). Thus, the lij interaction parameter of the NAHS is the only binary parameter available to tune the model. This binary parameter between Na+ and X (X = H2, O2 or N2) and between Cl− and X are taken equal since it is not possible to distinguish these two interactions independently in the brine. For H2 + salted water and O2 + salted water systems, the optimization of this parameter shows that a constant value (given in Tab. 5) is sufficient to reach a good accuracy as shown in Figure 5 and Figure 6 with an average deviation between experimental and calculated Henry constant of 3% and 8%, respectively. Note that for oxygen, experiments are not reported for fixed salinity values. Thus, the graphs in Figure 6 show experimental data gathered in specific salinity ranges.
 |
Fig. 5 Henry constant of hydrogen in salted water. Lines: this model. Symbols: experimental data from the parameterization database (Table 3). Blue diamonds: 0.5 mol/kg. Red squares: 1 mol/kg. Green triangles: 2 mol/kg. |
 |
Fig. 6 Henry constant of oxygen in salted water. Lines: this model for salinity of 0.9 mol/kg (blue), 3 mol/kg (green), and 5.3 mol/kg (orange). Symbols: experimental data. Blue diamonds: from 0.6 to 1 mol/kg. Green triangles: from 2.8 to 4 mol/kg. Orange circles: from 5.1 to 5.8 mol/kg. |
For the N2 + saline water system, a temperature dependency is found necessary to reach an acceptable average deviation (9%). The optimized parameters are reported in Table 5, and Figure 7 shows a comparison between experimental and calculated data.
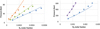 |
Fig. 7 N2 solubility in salted water at 303 K (left) and 398 K (right). Lines: this model. Symbols: experimental data. Blue triangles: 1 mol/kg. Green circles: 2.7 mol/kg. Orange diamonds: 5.5 mol/kg. Purple squares: 4.2 mol/kg. |
5 Model validation
For each system, a set of experimental data is excluded from the model parameterization database and is used to validate our model. The model is validated not only on its capability to correctly predict data not used in the parameterization database, but also to extrapolate to mixtures. This last validation is of primary importance to accurately evaluates phase equilibrium between brine and air for CAES units. Air is considered in this work as a mixture of N2 (80%mol.) and O2 (20%mol.). Table 3 provides a synthetic view of the references of experimental data used for both model parameterization and model validation.
For H2 + H2O, N2 + H2O, and O2 + H2O systems, the model predicts very satisfactory solubility data not used in the parameterization database, with an average deviation of 5%. The comparisons between experimental and predicted bubble curves are reported in the Supplementary Material (Fig. S1). More interestingly, the model predicts very well the water content in the vapor phase, as illustrated in Figure 8, with an average deviation of 3.5%. Finally, the extension of the model to multicomponent systems is also validated by its capacity to accurately predict air solubility in water in a large range of temperatures and pressure, as illustrated in Figure 9, with an average deviation of 7%.
 |
Fig. 8 Dew curves of H2 + H2O (left) and N2 + H2O (right). Lines: predictions with this model. Symbols: experimental data not used in the parameterization database [57]. Red squares: 366 K, green triangles: 422 K; blue diamonds: 310 K. |
 |
Fig. 9 Predictions of Air + H2O bubble curves at 1 bar (left) and 98 bar (right). Lines: this model. Symbols: experiments not used in parameterization database. |
As for gas + pure water systems, the model proposed for gas + salted water systems is validated on its capability to predict data not included in the parameterization database as indicated in Table 3. For the H2 + H2O + NaCl system, recent hydrogen solubility data are used for validation [8]. As illustrated in Figure 10, our model predicts with good accuracy these data in the whole temperature range (323 to 373 K) and salinity range (1–5 mol/kg). The average deviation between experiments and prediction is about 5%, while the experimental uncertainty estimated by the authors is very close (4%).
 |
Fig. 10 Predictions of hydrogen solubility in salted water at 323 K (left) and 373 K (right). Lines: this model. Symbols: experimental data not used in the parameterization database [8]. Orange diamonds: 1 mol/kg. Green triangles: 3 mol/kg. Blue circles: 5 mol/kg. |
For O2 + H2O + NaCl system, the recent experimental solubility data of Chabab et al. [52], not used in the parameterization database, are used to validate the model. As illustrated in Figure 11, the model predictions are found in good agreement with these experiments, with an average deviation of 7%. It can be nevertheless noticed that predictions are less accurate at the highest salinity (deviation of 15% at 4 mol/kg).
 |
Fig. 11 Predictions of oxygen solubility in salted water at 323 K (left) and 373 K (right). Lines: this model. Symbols: experimental data not used in the parameterization database [52]. Purple squares: 0.5 mol/kg. Orange diamonds: 1 mol/kg. Gray triangles: 4 mol/kg. |
For N2 + H2O + NaCl system, due to the lack of experimental data, all the existing data have been used for the model parameterization. Finally, for Air + H2O + NaCl, no data have been found in the literature to validate model predictions. It could be interesting for further studies to acquire new experimental data on such a system and compare them to our predictions.
6 Application to air storage in salt caverns
The e-PPC-SAFT equation of state parameterized in this work is used to evaluate some thermodynamic properties in the case of Compressed Air Energy Storage (CAES) in the salt cavern. Air is assumed to be a mixture of 80% N2 + 20% O2. The cavern considered in this study has a volume of 315.000 m3, with a residual volume of the brine of 20.000 m3. This brine is made of saturated halite (water + NaCl brine, with a salt concentration of 6 mol/kg). The following cycles are considered for this CAES: a cycle lasts for one day, constituted by 12 h of withdrawing during which both temperature and pressure decrease to the minimum storage conditions, and 12 h of injection during which temperature and pressure reach the maximum storage conditions. The pressure and temperature ranges have been obtained by using the GUSTv2 software [99, 100], modeling the air (20% O2 and 80% N2) thermodynamic behavior in the cavern and the heat transfer with the salt mass: the fluctuation of pressure and temperature obtained are 141–166 bar and 35–50 °C, respectively. The mass transfer between the air and the residual brine is not considered in this model. Injection and withdrawing flows are assumed constant for each cycle. An illustration of temperature and pressure variations during an 8 days operation is provided in Supplementary Material (Fig. S2).
For each temperature/pressure couple of the cycle, the e-PPC-SAFT model is used to evaluate the compressibility factor Z of the vapor phase. The evolution of this factor over the cycles is illustrated in Figure S3 of the Supplementary Material. This factor enables computing the total quantity of gas mixture in this phase. The e-PPC-SAFT is also used to compute phase equilibrium for each point of the cycle in order to determine more specifically the water content of the vapor phase. The knowledge of this gas water content during CAES operation is of primary importance, since water may increase corrosion issues in surface facilities and promote hydrate formation in pipes. Hence, Figure 12 illustrates the evolution of the water content in the gas produced during the cycles, as well as the corresponding mass of gaseous water present in the cavern. In order to highlight the effect of salinity, two calculations are carried out: in a hypothetical salt-free system, and a saturated halite brine, representative of salt caverns currently operated. The quantity of air solubilized in the brine is also plotted in Figure 13.
 |
Fig. 12 Prediction of the water content of the vapor phase (top), and its corresponding mass according to the dimensions of the cavern (bottom). Solid line: in a salt cavern, with residual brine at its bottom. Dashed line: in a hypothetical cavern with residual (salt-free) water. |
 |
Fig. 13 Prediction of the quantity of air solubilized in the residual brine. Solid line: in a salt cavern. Dashed line: in a hypothetical cavern with residual (salt-free) water. |
These figures show that in a salt cavern, with residual saturated brine at its bottom, the quantity of air solubilized is lower than what would be found in a hypothetical cavern with residual pure water, as a result of the “salting-out” effect. In presence of salt, water molecules mainly solvate ions and are less available to solubilize gas, leading also to lower volatility. As a result of the mass balance, the water content in the vapor phase is 30% less in salt cavern than in pure water. Note that the calculated quantities result only from thermodynamic considerations and neglect kinetic aspects, and more specifically the time needed to reach the thermodynamic equilibrium. Temperature gradients in the cavern are also neglected, although due to vaporization heat being absorbed in the brine-gas interface only, at the bottom of the cavern, while condensation heat release is distributed on the whole cavern volume, some conditions can create a cold gas layer just above the brine, preventing natural convection and may increase the time to reach this equilibrium in the whole cavern [101]. These assumptions necessarily cause an overestimation of the water content for short injection/withdrawing cycles. Nevertheless, this approach provides a first conservative estimation of gas moisture, useful to design surface dehydration units [102].
7 Conclusion
In this work, a parameterization of the e-PPC-SAFT equation of state has been carried out to predict phase equilibrium in salt caverns for hydrogen or compressed air storage. The amount of gas stored in the cavern being a key economical factor, the pure component parameters of the light gases (H2, N2, O2) have been fitted to accurately match reference compressibility factors. Deviations are in the same range of experimental uncertainties. The brine properties have also to be carefully modeled, to accurately predict gas solubilities, phase density, and water volatility. Brine is assumed to be a mixture of water, Na+, and Cl−, and model parameters have been fitted to match experimental mean ionic activity coefficients, brine vapor pressure, and brine densities. The average deviation between experimental and calculated data are 2.0, 1.3, and 1.4%, respectively, for temperatures ranging from 273 to 473 K, and salinities up to saturation (6 mol/kg). The solubility of the light gases is first investigated in pure water. For N2 and O2, a new Henry constant correlation is proposed based on a literature review of existing data, while for H2 an existing recent correlation is used. These correlations are used to fit the binary interaction parameters of the e-PPC-SAFT model between H2 + H2O, N2 + H2O, and O2 + H2O. Calculated Henry constants in pure water reproduce reference experimental correlation with good accuracy (average deviation less than 2%).
A similar approach is carried out for systems involving saline water. A literature review of the Henry constant of light gases in saline water is carried out, and binary interaction parameters of the e-PPC-SAFT model between H2 + ion, N2 + ion, and O2 + ion have been fitted to match experimental data. Average deviations between 3% and 9% are obtained, in the same range of experimental uncertainties.
This parameterized model is validated on its capability to accurately predict data or properties not used in the parameterization database, but also on its capability of predicting mixture properties. Thus, it has been used to predict Air + pure water phase equilibrium with good accuracy (deviation less than 7% on air molar fraction solubilized), the air being considered as a mixture of 80%mol. N2 + 20%mol. O2. The model has also been used to predict air + saline water phase equilibrium to evaluate the water content of the vapor phase for an application of CAES in a salt cavern. It can be noticed that there are no experimental data available for air + saline water phase equilibrium. Thus, it could be useful in further studies to acquire new experimental data and to compare the predictions generated by this new model. It is also worth noticing that the case study investigated in this work only deals with a thermodynamic approach. Kinetic and diffusive effects are neglected, but this approach can nevertheless be used as a first conservative evaluation to design surface dehydration units.
Supplementary material
 |
Figure S1.
Bubble curves of systems H2 + H2O (top left), N2 + H2O (top right) and O2 + H2O (bottom). Lines: predictions by the model. Symbols: experimental data not used in the model parameterization. Red squares: 366 K. Green triangles: 422 K. Blue diamonds: 373 K. Purple triangles: 436 K. |
 |
Figure S2.
Temperature and pressure variations during 8 cycles of CAES unit. Solid line: temperature. Dashed lines: pressure. |
 |
Figure S3.
Evolution of the vapour phase compressibility factor during the cycles, calculated from the e-PPC-SAFT model. |
References
- Gross R., Leach M., Bauen A. (2003) Progress in renewable energy, Environ. Int. 29, 1, 105–122. https://doi.org/10.1016/S0160-4120(02)00130-7. [CrossRef] [Google Scholar]
- Gallo A.B., Simões-Moreira J.R., Costa H., Santos M.M., Moutinho dos Santos E. (2016) Energy storage in the energy transition context: A technology review, Renewable Sustainable Energy Rev. 65, 800–822. https://doi.org/10.1016/j.rser.2016.07.028. [CrossRef] [Google Scholar]
- Ozarslan A. (2012) Large-scale hydrogen energy storage in salt caverns, Int. J. Hydrogen Energy 37, 19, 14265–14277. https://doi.org/10.1016/j.ijhydene.2012.07.111. [CrossRef] [Google Scholar]
- Panfilov M. (2015) Underground and pipeline hydrogen storage, in: B. Subramani, et al. (eds.), Compendium of hydrogen energy, Woodhead Publishing, Sawston, United Kingdom, pp. 91–115. [Google Scholar]
- Réveillère A., Londe L. (2017) Compressed air energy storage: A new beginning? Geostock, France, in: Solution Mining Research Institute Technical Conference, 24–27 September 2017, Münster, Germany. [Google Scholar]
- Lopez-Lazaro C., Bachaud P., Moretti I., Ferrando N. (2019) Predicting the phase behavior of hydrogen in NaCl brines by molecular simulation for geological applications, BSGF – Earth Sci. Bull. 190. https://doi.org/10.1051/bsgf/2019008. [Google Scholar]
- Søreide I., Whitson C.H. (1992) Peng-Robinson predictions for hydrocarbons, CO2, N2 and H2S with pure water and NaCI brine, Fluid Phase Equilib. 77, 217–240. [CrossRef] [Google Scholar]
- Chabab S., Théveneau P., Coquelet C., Corvisier J., Paricaud P. (2020) Measurements and predictive models of high-pressure H2 solubility in brine (H2O+NaCl) for underground hydrogen storage application, Int. J. Hydrogen Energy 45, 56, 32206–32220. [CrossRef] [Google Scholar]
- Schlaikjer A., Thomsen K., Kontogeorgis G.M. (2018) eCPA: An ion-specific approach to parametrization, Fluid Phase Equilib. 470, 176–187. https://doi.org/10.1016/j.fluid.2017.12.008. [CrossRef] [Google Scholar]
- Li D., Beyer C., Bauer S. (2018) A unified phase equilibrium model for hydrogen solubility and solution density, Int. J. Hydrogen Energy 43, 1, 512–529. https://doi.org/10.1016/j.ijhydene.2017.07.228. [CrossRef] [Google Scholar]
- Roa Pinto J.S., Bachaud P., Fargetton T., Ferrando N., Jeannin L., Louvet F. (2021) Modeling phase equilibrium of hydrogen and natural gas in brines: Application to storage in salt caverns, Int. J. Hydrogen Energy 46, 5, 4229–4240. https://doi.org/10.1016/j.ijhydene.2020.10.242. [CrossRef] [Google Scholar]
- Zhu Z., Cao Y., Zheng Z., Chen D. (2022) An accurate model for estimating H2 solubility in pure water and aqueous NaCl solutions, Energies 15, 14. https://doi.org/10.3390/en15145021. [Google Scholar]
- Torín-Ollarves G.A., Trusler J.M. (2021) Solubility of hydrogen in sodium chloride brine at high pressures, Fluid Phase Equilib. 539, 113025. https://doi.org/10.1016/j.fluid.2021.113025. [CrossRef] [Google Scholar]
- van Rooijen W.A., Habibi P., Xu K., Dey P., Vlugt T.J.H., Hajibeygi H., Moultos O.A. (2023) Interfacial tensions, solubilities, and transport properties of the H2/H2O/NaCl system: A molecular simulation study, J. Chem. Eng. Data, https://doi.org/10.1021/acs.jced.2c00707. [Google Scholar]
- Chabab S., Cruz J.L., Poulain M., Ducousso M., Contamine F., Serin J.P., Cézac P. (2021) Thermodynamic modeling of mutual solubilities in gas-laden brines systems containing CO2, CH4, N2, O2, H2, H2O, NaCl, CaCl2, and KCl: Application to degassing in geothermal processes, Energies 14, 17. https://doi.org/10.3390/en14175239. [CrossRef] [Google Scholar]
- Ahmed S., Ferrando N., de Hemptinne J.-C., Simonin J.-P., Bernard O., Baudouin O. (2016) A new PC-SAFT model for pure water, water–hydrocarbons, and water–oxygenates systems and subsequent modeling of VLE, VLLE, and LLE, J. Chem. Eng. Data 61, 12, 4178–4190. https://doi.org/10.1021/acs.jced.6b00565. [CrossRef] [Google Scholar]
- Gross J., Sadowski G. (2002) Application of the perturbed-chain SAFT equation of state to associating systems, Ind. Eng. Chem. Res. 41, 22, 5510–5515. https://doi.org/10.1021/ie010954d. [Google Scholar]
- Boublik T. (1970) Hard sphere equation of state, J. Chem. Phys. 53, 471–473. [CrossRef] [Google Scholar]
- Mansoori G.A., Carnahan N.F., Starling K.E., Leland T.W.J. (1971) Equilibrium thermodynamic properties of the mixture of hard spheres, J. Chem. Phys. 54, 4, 1523–1525. [CrossRef] [Google Scholar]
- Wertheim M.S. (1984) Fluids with Highly directional attractive forces. I. Statistical thermodynamics, J. Stat. Phys. 35, 19–34. [CrossRef] [MathSciNet] [Google Scholar]
- Chapman W.G., Jackson G., Gubbins K.E. (1988) Phase equilibria of associating fluids: Chain molecules with multiple bonding sites, Mol. Phys. 65, 1057–1079. [CrossRef] [Google Scholar]
- Nguyen-Huynh D., Passarello J.-P., Tobaly P., de Hemptinne J.-C. (2008) Application of GC-SAFT EOS to polar systems using a segment approach, Fluid Phase Equilib. 264, 1, 62–75. https://doi.org/10.1016/j.fluid.2007.10.019. [CrossRef] [Google Scholar]
- Jog P., Chapman W.G. (1999) Application of Wertheim's thermodynamic Perturbation theory to dipolar hard sphere chains, Mol. Phys. 97, 3, 307–319. [CrossRef] [Google Scholar]
- Trinh T.-K.-H., Passarello J.-P., de Hemptinne J.-C., Lugo R., Lachet V. (2016) A non-additive repulsive contribution in an equation of state: The development for homonuclear square well chains equation of state validated against Monte Carlo simulation, J. Chem. Phys. 144, 3, 124902. https://doi.org/10.1063/1.4944068. [CrossRef] [PubMed] [Google Scholar]
- Lyra Paredes M.L., dos Reis R.A., Tavares F.W. (2009) Inner segment radial distribution functions at contact point for chain-like molecules, J. Mol. Liq. 147, 3, 198–210. https://doi.org/10.1016/j.molliq.2009.04.005. [CrossRef] [Google Scholar]
- Liu Z., Wang W., Li Y. (2005) An equation of state for electrolyte solutions by a combination of low-density expansion of non-primitive mean spherical approximation and statistical associating fluid theory, Fluid Phase Equilib. 227, 2, 147–156. https://doi.org/10.1016/j.fluid.2004.11.007. [CrossRef] [Google Scholar]
- Schreckenberg J.M., Dufal S., Haslam A.J., Adjiman C.S., Jackson G., Galindo A. (2014) Modelling of the thermodynamic and solvation properties of electrolyte solutions with the statistical associating fluid theory for potentials of variable range, Mol. Phys. 112, 17, 2339–2364. https://doi.org/10.1080/00268976.2014.910316. [CrossRef] [Google Scholar]
- Tan S.P., Adidharma H., Radosz M. (2005) Statistical associating fluid theory coupled with restricted primitive model to represent aqueous strong electrolytes, Ind. Eng. Chem. Res. 44, 12, 4442–4452. https://doi.org/10.1021/ie048750v. [CrossRef] [Google Scholar]
- Lee B.-S., Kim K.-C. (2009) Modeling of aqueous electrolyte solutions based on perturbed-chain statistical associating fluid theory incorporated with primitive mean spherical approximation. Korean J. Chem. Eng. 26, 6, 1733–1747. [CrossRef] [Google Scholar]
- Rozmus J., de Hemptinne J.C., Galindo A., Dufal S., Mougin P. (2013) Modeling of strong electrolytes with ePPC-SAFT up to high temperatures, Ind. Eng. Chem. Res. 52, 9979–9994. https://doi.org/10.1021/ie303527j. [CrossRef] [Google Scholar]
- Shadloo A., Abolala M., Peyvandi K. (2016) Application of ion-based ePC-SAFT in prediction of density of aqueous electrolyte solutions, J. Mol. Liq. 221, 904–913. https://doi.org/10.1016/j.molliq.2016.06.043. [CrossRef] [Google Scholar]
- Selam M.A., Economou I.G., Castier M. (2018) A thermodynamic model for strong aqueous electrolytes based on the eSAFT-VR Mie equation of state, Fluid Phase Equilib. 464, 47–63. https://doi.org/10.1016/j.fluid.2018.02.018. [CrossRef] [Google Scholar]
- Maribo-Mogensen B., Kontogeorgis G., Thomsen K. (2012) Comparison of the Debye-Hückel and the mean spherical approximation theories for electrolyte solutions, Ind. Eng. Chem. Res. 51, 14, 5353–5363. [CrossRef] [Google Scholar]
- Fawcett W.R. (1999) Thermodynamic parameters for the solvation of monatomic ions in water, J. Phys. Chem. B 103, 50, 11181–11185. https://doi.org/10.1021/jp991802n. [CrossRef] [Google Scholar]
- Pottel R. (1973) Dielectric properties, in: Franks F.(ed.), Water: a comprehensive treatise; Volume 3: Aqueous properties of simple electrolytes, Plenum Press. [Google Scholar]
- NIST and TRC database (2011) Version 2-2011-3-Pro. , National Institute of Standards and Technology/Thermodynamics and Thermodynamics Research Center. [Google Scholar]
- Gibbard H.F. Jr, Scatchard G., Rousseau R.A., Creek J.L. (1974) Liquid-vapor equilibrium of aqueous sodium chloride, from 298 to 373 K and from 1 to 6 mol kg−1, and related properties, J. Chem. Eng. Data 19, 3, 281–288. [CrossRef] [Google Scholar]
- Mokbel I., Ye S., Jose J., Xans P. (1997) Study of non ideality of various aqueous sodium chloride solutions by vapor pressure measurements and correlation of experimental results by Pitzer’s method, J. Chim. Phys. PCB 94, 122–137. [CrossRef] [EDP Sciences] [Google Scholar]
- Liu C.T., Lindsay W.T. Jr (1972) Thermodynamics of sodium chloride solutions at high temperatures, J. Sol. Chem. 1, 1, 45–69. [CrossRef] [Google Scholar]
- Rogers P.S.Z., Pitzer K.S. (1982) Volumetric properties of aqueous sodium chloride solutions, J. Phys. Chem. Ref. Data 11, 1, 15–81. [CrossRef] [Google Scholar]
- Trinh T.-K.-H., de Hemptinne J.-C., Lugo R., Ferrando N., Passarello J.-P. (2016) Hydrogen solubility in hydrocarbon and oxygenated organic compounds, J. Chem. Eng. Data 61, 1, 19–34. https://doi.org/10.1021/acs.jced.5b00119. [CrossRef] [Google Scholar]
- Rowley R.L., Wilding W.V., Oscarson J.L., Knotts T.A. (2006) DIPPR® data compilation of pure chemical properties, Design Institute for Physical Property Data, AIChE, New York, NY. [Google Scholar]
- Gamsjäger H., Lorimer J.W., Salomon M., Shaw D.G., Tomkins R.P.T. (2010) The IUPAC-NIST solubility data series: A guide to preparation and use of compilations and evaluations, J. Phys. Chem. Ref. Data 39, 2. [Google Scholar]
- Morrison T.J., Billett F. (1952) The salting-out of non-electrolytes. Part II. The effect of variation in non-electrolyte, J. Chem. Soc., 3819–3822. https://doi.org/10.1039/JR9520003819. [CrossRef] [Google Scholar]
- Gordon L.I., Cohen Y., Standley D.R. (1977) The solubility of molecular hydrogen in seawater, Deep-Sea Res. 24, 937–941. [CrossRef] [Google Scholar]
- Steiner P. (1894) Ueber die Absorption des Wasserstoffs im Wasser und in wässerigen Lösungen, Ann. Phys. 288, 6, 275–299. https://doi.org/10.1002/andp.18942880605. [CrossRef] [Google Scholar]
- Crozier T.E., Yamamoto S. (1974) Solubility of hydrogen in water, sea water, and sodium chloride solutions, J. Chem. Eng. Data 19, 3, 242–244. https://doi.org/10.1021/je60062a007. [CrossRef] [Google Scholar]
- Cramer S.D. (1982) The solubility of methane, carbon dioxide, and oxygen in brines from 0 degrees to 300 °C, Bur. Mines Rep. Invest. RI 8706, 1–17. [Google Scholar]
- Iwai Y., Eya H., Itoh Y., Aral Y., Takeuchi K. (1993) Measurement and correlation of solubilities of oxygen in aqueous solutions containing salts and sucrose, Fluid Phase Equilib. 83, 271–278. https://doi.org/10.1016/0378-3812(93)87030-5. [CrossRef] [Google Scholar]
- MacArthur C.G. (1916) Solubility of oxygen in salt solutions and the hydrates of these salts, J. Phys. Chem. 20, 495–502. https://doi.org/10.1021/j150168a003. [CrossRef] [Google Scholar]
- Lang W., Zander R. (1986) Salting-out of oxygen from aqueous electrolyte solutions: Prediction and measurement, Ind. Eng. Chem. Fund. 25, 4, 775–782. https://doi.org/10.1021/i100024a050. [CrossRef] [MathSciNet] [Google Scholar]
- Chabab S., Ahmadi P., Théveneau P., Coquelet C., Chapoy A., Corvisier J., Paricaud P. (2021) Measurements and modeling of high-pressure O2 and CO2 solubility in brine (H2O + NaCl) between 303 and 373 K and pressures up to 36 MPa, J. Chem. Eng. Data 66, 1, 609–620. https://doi.org/10.1021/acs.jced.0c00799. [CrossRef] [Google Scholar]
- Braun L. (1900) The absorption of nitrogen and hydrogen in aqueous solutions of various dissociated substances, Z. Phys. Chem. Stoechiom. Verwandtschaftsl. 33, 721–739. [CrossRef] [Google Scholar]
- van Slyke D., Dillon R.T., Margaria R. (1934) Studies of gas and electrolyte equilibria in blood XVIII. Solubility and physical state of atmospheric nitrogen in blood cells and plasma, J. Biol. Chem. 105, 571–596. [CrossRef] [Google Scholar]
- Smith N.O., Kelemen S., Nagy B. (1962) Solubility of natural gases in aqueous salt solutions – II: Nitrogen in aqueous NaCl, CaCl2, Na2SO4 and MgSO4 at room temperatures and at pressures below 1000 psia, Geochim. Cosmochim. Acta 26, 9, 921–926. https://doi.org/10.1016/0016-7037(62)90066-2. [CrossRef] [Google Scholar]
- O’Sullivan T.D., Smith N.O. (1970) The solubility and partial molar volume of Nitrogen and methane in water and in aqueous sodium chloride from 50 to 125 °C and 100 to 600 Atm, J. Phys. Chem. 74, 7, 1460–1466. [CrossRef] [Google Scholar]
- Gillespie P.C., Wilson G.M. (1980) Vapor-liquid equilibrium data on water-substitute gas components: N2-H2O, H2-H2O, CO-H2O, H2-CO-H2O and H2S-H2O, GPA Research Report RR-41. [Google Scholar]
- Alvarez J., Crovetto R., Fernandez-Prini R. (1988) The dissolution of N2 and of H2 in water from room temperature to 640 K, Ber. Bunsen-Ges. Phys. Chem. 92, 935–940. [CrossRef] [Google Scholar]
- Tokunaga J. (1975) Solubilities of oxygen, nitrogen, and carbon dioxide in aqueous alcohol solutions, J. Chem. Eng. Data 20, 1, 41–46. https://doi.org/10.1021/je60064a025. [CrossRef] [Google Scholar]
- Morrison T.J., Billett F. (1948) 413. The measurement of gas solubilities, J. Chem. Soc. 2033–2035. https://doi.org/10.1039/JR9480002033.. [CrossRef] [Google Scholar]
- Yamamoto H., Kamei H., Tokunaga J. (1994) Solubilities of argon, oxygen and nitrogen in 1,2-propanediol + water mixed solvent at 298.15 K and 101.33 kPa, J. Chem. Eng. Jpn. 27, 4, 455–459. https://doi.org/10.1252/jcej.27.455. [CrossRef] [Google Scholar]
- Yamamoto H., Tokunaga J. (1994) Solubilities of nitrogen and oxygen in 1,2-ethanediol + water at 298.15 K and 101.33 kPa, J. Chem. Eng. Data 39, 3, 544–547. https://doi.org/10.1021/je00015a033. [CrossRef] [Google Scholar]
- Yasunishi A. (1977) Solubilities of sparingly soluble gases in aqueous sodium sulfate and sulfite solutions, J. Chem. Eng. Jpn. 10, 2, 89–94. https://doi.org/10.1252/jcej.10.89. [CrossRef] [Google Scholar]
- Adeney W.E., Becker H.G. (1919) XXVIII. The determination of the rate of solution of atmospheric nitrogen and oxygen by water. Part I, Lond. Edinb. Dubl. Phil. Mag. J. Sci., Science 38, 225, 317–337. https://doi.org/10.1080/14786440908635955. [CrossRef] [Google Scholar]
- Behnke A.R., Yarbrough O.D. (1939) Respiratory resistance, oil-water solubility, and mental effects of argon, compared with helium and nitrogen, Am. J. Physiol. – Legacy Content 126, 2, 409–415. https://doi.org/10.1152/ajplegacy.1939.126.2.409. [CrossRef] [Google Scholar]
- Bunsen R. (1855) XV. On the law of absorption of gases, Lond. Edinb. Dubl. Phil. Mag. J. Sci. 9, 57, 116–130. https://doi.org/10.1080/14786445508641836. [CrossRef] [Google Scholar]
- Douglas E. (1964) Solubilities of oxygen, argon, and nitrogen in distilled water, J. Phys. Chem. 68, 1, 169–174. https://doi.org/10.1021/j100783a028. [CrossRef] [Google Scholar]
- Fox C.J.J. (1909) On the coefficients of absorption of nitrogen and oxygen in distilled water and sea-water, and of atmospheric carbonic acid in sea-water, T. Faraday Soc. 5, 68–86. https://doi.org/10.1039/TF9090500068. [CrossRef] [Google Scholar]
- Murray C.N., Riley J.P., Wilson T. (1969) The solubility of gases in distilled water and sea water – I. Nitrogen, Deep Sea Res. Oceanogr. Abs. 16, 3, 297–310. https://doi.org/10.1016/0011-7471(69)90020-5. [CrossRef] [Google Scholar]
- Orcutt F.S., Seevers M.H. (1937) A method for determining the solubility of gases in pure liquids or solutions by the van Slyke-Neill manometric apparatus, J. Biol. Chem. 117, 2, 501–507. https://doi.org/10.1016/S0021-9258(18)74550-X. [CrossRef] [Google Scholar]
- van Slyke D.D. (1939) Determination of solubilities of gases in liquids with use of the van Slyke-Neill manometric apparatus for both saturation and analysis, J. Biol. Chem. 130, 2, 545–554. https://doi.org/10.1016/S0021-9258(18)73525-4. [CrossRef] [Google Scholar]
- Cosgrove B.A., Walkley J. (1981) Solubilities of gases in H2O and 2H2O, J. Chromatogr. A 216, 161–167. https://doi.org/10.1016/S0021-9673(00)82344-4. [CrossRef] [Google Scholar]
- Krieger I.M., Mulholland G.W., Dickey C.S. (1967) Diffusion coefficients for gases in liquids from the rates of solution of small gas bubbles, J. Phys. Chem. 71, 4, 1123–1129. https://doi.org/10.1021/j100863a051. [CrossRef] [Google Scholar]
- Rischbieter E., Schumpe A., Wunder V. (1996) Gas solubilities in aqueous solutions of organic substances, J. Chem. Eng. Data 41, 4, 809–812. https://doi.org/10.1021/je960039c. [CrossRef] [Google Scholar]
- Romero C.M., Garzon L.C., Blanco L.H., Suarez A.F. (2014) Solubility of argon and nitrogen in aqueous solutions of dodecyltrimethylammonium bromide (DTAB) from 283.15 to 298.15 K and 101325 Pa partial pressure of gas, J. Sol. Chem. 43, 6, 1147–1155. https://doi.org/10.1007/s10953-014-0188-x. [CrossRef] [Google Scholar]
- Wilcock R.J., Battino R. (1974) Solubility of oxygen-nitrogen mixture in water, Nature 252, 5484, 614–615. https://doi.org/10.1038/252614c0. [CrossRef] [Google Scholar]
- Benson B.B., Krause D. (1976) Empirical laws for dilute aqueous solutions of nonpolar gases, J. Chem. Phys. 64, 2, 689–709. https://doi.org/10.1063/1.432215. [CrossRef] [Google Scholar]
- Cassuto L. (1903) Sulla solubilità dei gas nei liqdidi, Il Nuovo Cimento (1901–1910) 6, 1, 5–20. https://doi.org/10.1007/BF02718805. [CrossRef] [Google Scholar]
- Costa Gomes M.F., Grolier J.-P. (2001) Determination of Henry’s law constants for aqueous solutions of tetradeuteriomethane between 285 and 325 K and calculation of the H/D isotope effect, Phys. Chem. Chem. Phys. 3, 6, 1047–1052. https://doi.org/10.1039/B008755F. [CrossRef] [Google Scholar]
- Wise D.L., Houghton G. (1969) Solubilities and diffusivities of oxygen in hemolyzed human blood solutions, Biophys. J. 9, 1, 36–53. https://doi.org/10.1016/S0006-3495(69)86367-8. [CrossRef] [Google Scholar]
- Morgan J.L.R., Richardson A.H. (1930) Solubility relations in gas-liquid systems. IV, J. Phys. Chem. 34, 10, 2356–2366. https://doi.org/10.1021/j150316a018. [CrossRef] [Google Scholar]
- Lubarsch O. (1889) Ueber die Absorption von Gasen in Gemischen von Alkohol und Wasser, Ann. Phys. 273, 7, 524–525. https://doi.org/10.1002/andp.18892730714. [CrossRef] [Google Scholar]
- Metschl J. (1924) The supersaturation of gases in water and certain organic liquids, J. Phys. Chem. 28, 5, 417–437. https://doi.org/10.1021/j150239a001. [CrossRef] [Google Scholar]
- Millero F.J., Huang F., Graham T.B. (2003) Solubility of oxygen in some 1-1, 2-1, 1-2, and 2-2 electrolytes as a function of concentration at 25 °C, J. Sol. Chem. 32, 6, 473–487. https://doi.org/10.1023/A:1025301314462. [CrossRef] [Google Scholar]
- Millero F.J., Huang F., Laferiere A.L. (2002) Solubility of oxygen in the major sea salts as a function of concentration and temperature, Mar. Chem. 78, 4, 217–230. https://doi.org/10.1016/S0304-4203(02)00034-8. [CrossRef] [Google Scholar]
- Millero F.J., Huang F., Laferiere A.L. (2002) The solubility of oxygen in the major sea salts and their mixtures at 25 °C, Geochim. Cosmochim. Acta 66, 13, 2349–2359. https://doi.org/10.1016/S0016-7037(02)00838-4. [CrossRef] [Google Scholar]
- Millero F.J., Huang F. (2003) Solubility of oxygen in aqueous solutions of KCl, K2SO4, and CaCl2 as a function of concentration and temperature, J. Chem. Eng. Data 48, 4, 1050–1054. https://doi.org/10.1021/je034031w. [CrossRef] [Google Scholar]
- Montgomery H.A.C., Thom N.S., Cockburn A. (1964) Determination of dissolved oxygen by the winkler method and the solubility of oxygen in pure water and sea water, J. Appl. Chem. 14, 7, 280–296. https://doi.org/10.1002/jctb.5010140704. [Google Scholar]
- Stephan E.F., Hatfield N.N., Peoples R.S., Pray H. (1956) The solubility of gases in water and aqueous uranyl salt solutions at elevated temperatures and pressures, Battelle Mem. Inst. Rep. 1–47. [Google Scholar]
- Rakestraw N.W., Emmel V.M. (1937) The determination of dissolved nitrogen in water, Ind. Eng. Chem. Anal. 9, 7, 344–346. https://doi.org/10.1021/ac50111a020. [CrossRef] [Google Scholar]
- Pettersson O., Sondén K. (1889) Ueber das Absorptionsvermögen des Wassers für die atmosphärischen Gase, Ber. Dtsch. Chem. Ges. 22, 1, 1439–1446. https://doi.org/10.1002/cber.188902201301. [CrossRef] [Google Scholar]
- Nguyen-Huynh D., Tran T.K.S., Tamouza S., Passarello J.P., Tobaly P., de Hemptinne J.C. (2008) Modeling phase equilibria of asymmetric mixtures using a group-contribution SAFT (GC-SAFT) with a k(ij) correlation method based on London’s theory. 2. Application to binary mixtures containing aromatic hydrocarbons, n-alkanes, CO2, N2, and H2S, Ind. Eng. Chem. Res. 47, 22, 8859–8868. [CrossRef] [Google Scholar]
- Trinh T.-K.-H., Passarello J.-P., de Hemptinne J.-C., Lugo R. (2016) Use of a non additive GC-PPC-SAFT equation of state to model hydrogen solubility in oxygenated organic compounds, Fluid Phase Equilib. 429, 177–195. https://doi.org/10.1016/j.fluid.2016.08.003. [CrossRef] [Google Scholar]
- Gross J., Sadowski G. (2001) Perturbed-Chain SAFT: An equation of state based on a perturbation theory for chain molecules, Ind. Eng. Chem. Res. 40, 1244–1260. [CrossRef] [Google Scholar]
- Diamantonis N.I., Economou I.G. (2011) Evaluation of statistical associating fluid theory (SAFT) and perturbed chain-SAFT equations of state for the calculation of thermodynamic derivative properties of fluids related to carbon capture and sequestration, Energ Fuel 25, 7, 3334–3343. https://doi.org/10.1021/ef200387p. [CrossRef] [Google Scholar]
- Ghosh A., Chapman W.G., French R.N. (2003) Gas solubility in hydrocarbons – A SAFT-based approach, Fluid Phase Equilib. 209, 2, 229–243. [CrossRef] [Google Scholar]
- Alanazi A., Bawazeer S., Ali M., Keshavarz A., Hoteit H. (2022) Thermodynamic modeling of hydrogen–water systems with gas impurity at various conditions using cubic and PC-SAFT equations of state, Energy Convers. Manag. X 15, 100257. https://doi.org/10.1016/j.ecmx.2022.100257. [Google Scholar]
- Marcus Y., Hefter G. (2006) Ion pairing, Chem. Rev. 106, 11, 4585–4621. https://doi.org/10.1021/cr040087x. [CrossRef] [PubMed] [Google Scholar]
- Karimi-Jafari M., Gatelier N., Geostock, France (2016) SFRI Fall Meeting, Salzburg, Austria. [Google Scholar]
- Réveillère A., de Laguérie P., Gruget R., Nancy T., Guénel L.,, Geostock, France (2015) SMRI Spring Meeting Rochester, 27–28 April 2015, Rochester, New York, USA. [Google Scholar]
- Bérest P. (2019) Heat transfer in salt caverns, Int. J. Rock Mech. Min. Sci. 120, 82–95. https://doi.org/10.1016/j.ijrmms.2019.06.009. [CrossRef] [Google Scholar]
- Louvet F., Charnavel Y., Portenabe J.C. (2018) Moisture content of gas in salt caverns surface measurements, in: SMRI Fall Meeting Belfast. [Google Scholar]
All Tables
Pure component parameters in the e-PPC-SAFT model. Parameters in bold are those adjusted in this work. For O2, N2, and H2, parameters are adjusted on compressibility factors. For ions, parameters are adjusted on MIAC, brine vapor pressures, and brine densities.
All Figures
 |
Fig. 1 Experimental Henry constants of N2 and O2 in pure water. Blue diamonds: from direct Henry constant data. Red squares: from Ostwald coefficient data. Green triangles: from Kuenen coefficient data. Purple crosses: from Bunsen coefficient data. Blue stars: from PTx data. The solid line is a fit of all data with correlation 38. The dotted lines are guides indicated ±10% from the correlation. |
| In the text | |
 |
Fig. 2 Compressibility factor of H2, N2, and O2. Symbols: reference date from NIST database [36]. Lines: this model. |
| In the text | |
 |
Fig. 3 NaCl MIAC, vapor pressure, and density of NaCl aqueous solutions. Symbols: experimental data [37–40]. Lines: this model. |
| In the text | |
 |
Fig. 4 Henry constant of H2 (diamonds), N2 (triangles), and O2 (circles) in pure water. Symbols: experimental data (Eq. (38)). Lines: this model. |
| In the text | |
 |
Fig. 5 Henry constant of hydrogen in salted water. Lines: this model. Symbols: experimental data from the parameterization database (Table 3). Blue diamonds: 0.5 mol/kg. Red squares: 1 mol/kg. Green triangles: 2 mol/kg. |
| In the text | |
 |
Fig. 6 Henry constant of oxygen in salted water. Lines: this model for salinity of 0.9 mol/kg (blue), 3 mol/kg (green), and 5.3 mol/kg (orange). Symbols: experimental data. Blue diamonds: from 0.6 to 1 mol/kg. Green triangles: from 2.8 to 4 mol/kg. Orange circles: from 5.1 to 5.8 mol/kg. |
| In the text | |
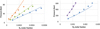 |
Fig. 7 N2 solubility in salted water at 303 K (left) and 398 K (right). Lines: this model. Symbols: experimental data. Blue triangles: 1 mol/kg. Green circles: 2.7 mol/kg. Orange diamonds: 5.5 mol/kg. Purple squares: 4.2 mol/kg. |
| In the text | |
 |
Fig. 8 Dew curves of H2 + H2O (left) and N2 + H2O (right). Lines: predictions with this model. Symbols: experimental data not used in the parameterization database [57]. Red squares: 366 K, green triangles: 422 K; blue diamonds: 310 K. |
| In the text | |
 |
Fig. 9 Predictions of Air + H2O bubble curves at 1 bar (left) and 98 bar (right). Lines: this model. Symbols: experiments not used in parameterization database. |
| In the text | |
 |
Fig. 10 Predictions of hydrogen solubility in salted water at 323 K (left) and 373 K (right). Lines: this model. Symbols: experimental data not used in the parameterization database [8]. Orange diamonds: 1 mol/kg. Green triangles: 3 mol/kg. Blue circles: 5 mol/kg. |
| In the text | |
 |
Fig. 11 Predictions of oxygen solubility in salted water at 323 K (left) and 373 K (right). Lines: this model. Symbols: experimental data not used in the parameterization database [52]. Purple squares: 0.5 mol/kg. Orange diamonds: 1 mol/kg. Gray triangles: 4 mol/kg. |
| In the text | |
 |
Fig. 12 Prediction of the water content of the vapor phase (top), and its corresponding mass according to the dimensions of the cavern (bottom). Solid line: in a salt cavern, with residual brine at its bottom. Dashed line: in a hypothetical cavern with residual (salt-free) water. |
| In the text | |
 |
Fig. 13 Prediction of the quantity of air solubilized in the residual brine. Solid line: in a salt cavern. Dashed line: in a hypothetical cavern with residual (salt-free) water. |
| In the text | |
 |
Figure S1.
Bubble curves of systems H2 + H2O (top left), N2 + H2O (top right) and O2 + H2O (bottom). Lines: predictions by the model. Symbols: experimental data not used in the model parameterization. Red squares: 366 K. Green triangles: 422 K. Blue diamonds: 373 K. Purple triangles: 436 K. |
| In the text | |
 |
Figure S2.
Temperature and pressure variations during 8 cycles of CAES unit. Solid line: temperature. Dashed lines: pressure. |
| In the text | |
 |
Figure S3.
Evolution of the vapour phase compressibility factor during the cycles, calculated from the e-PPC-SAFT model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




